Sprawozdanie z Ćwiczenia 11/B-9

Wydział	Dzień Poniedziałek 11-14			Nr zespołu
Inżynierii Środowiska	Data 17-04-2000			12
Nazwisko i Imię	Ocena z przygotowania		Ocena ze sprawozdania	Ocena
Prowadzący: W. Tłaczała		Podpis
		Prowadzącego

Temat: Badanie osłabienia promieniowania γ przy przechodzeniu przez materię.

1. Cel ćwiczenia.

Pomiary natężenia wiązki w zależności od grubości i rodzaju absorbenta z kolimatorem dla określonego źródełka promieniotwórczego. Do badania wykorzystaliśmy źródło promieniowania γ­­­­ ­⁶⁰Co, a role absorbentów spełniały ²⁰⁷Pb, ⁶³Cu, ²⁶Al.

2. Część teoretyczna.

Tempo wszystkich rozpadów promieniotwórczych opisuje ta sama zależność zwana również prawem rozpadu promieniotwórczego:

N_o - liczba zliczeń,

N(x) - liczba zliczeń pochodząca od kwantów γ przy braku materiału osłabiającego,

μ - współczynnik osłabienia,

x - grubość absorbentu.

Promieniowanie γ przechodząc przez ośrodek materialny ulega osłabieniu. Osłabienie to jest wykładniczo zależne od grubości absorbenta.

Promieniowanie γ działa zarówno na elektrony jak i na jądra atomowe. Podstawowymi procesami osłabiającymi wiązkę promieniowania są:

• rozpraszanie komptonowskie,

• zjawisko fotoelektryczne,

• zjawisko tworzenia par elektron-pozytron.

W ćwiczeniu wykorzystujemy prawo osłabienia wiązki promieniowania γ przy przechodzeniu przez materię. Mówi ono, że podczas przechodzenia promieni γ przez warstwę materii część fotonów ulega wyeliminowaniu. Ubytek fotonów jest wtedy definiowany wzorem:

-dN=μNdx

μ - współczynnik proporcjonalności (współczynnik osłabienia próbki)

N - liczba fotonów

dx - grubość absorbentu

3. Schemat stanowiska badawczego

4. Wykonanie ćwiczenia

Po włączeniu aparatury zmierzyliśmy tło w czasie 10s. Następnie dla określonego źródełka promieniotwórczego wykonaliśmy serię pomiarów natężenia wiązki w zależności od grubości absorbentów, którymi były: ołów, miedz i aluminium.

5. Wyniki pomiarów

Tabela 1. Widmo tła - pomiar trwał 10 s.

Napięcie progowe [V]	2,0	2,5	3,0	3,5	4,0	4,5	5,0	5,5	6,0	6,5
Liczba zliczeń [imp/min]	2318	1174	885	363	390	1752	868	17	5	3

Wykres 1. Widmo tła.

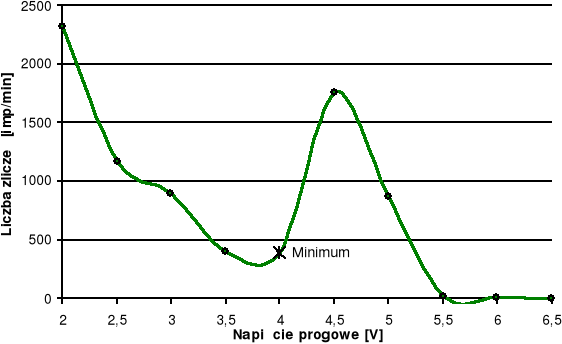
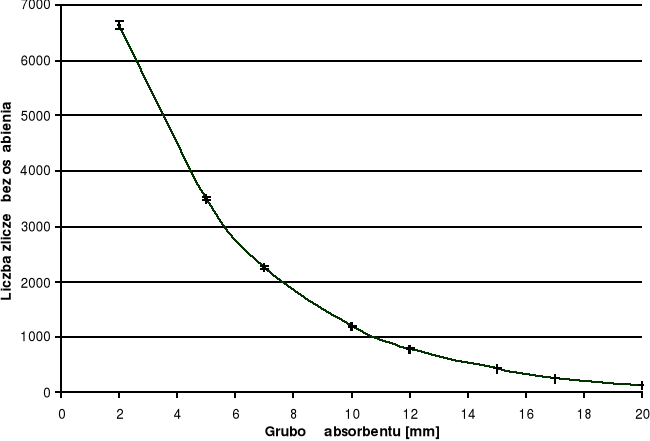
Tabela 2. Wyniki pomiaru promieniowania γ w zależności od grubości i rodzaju absorbenta.

Grubość absorbentu [mm]	2	5	7	10	12	15	17	20
N0 - Liczba zliczeń dla Pb	8221	5986	4779	3499	2862	2151	1609	1147
N0 - Liczba zliczeń dla Cu	9260	7770	7159	6058	5440	4752	4257	3625
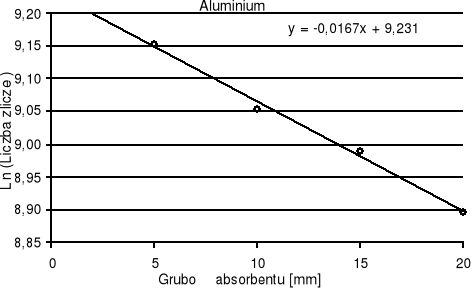
N0 - Liczba zliczeń dla Al	-	9438	-	8543	-	8015	-	7302

6. Opracowanie wyników

1. Do obliczenia ilości wyładowań kwantów gamma bez absorbenta wykorzystaliśmy wzór:

N(x) - liczba zliczeń pochodząca od kwantów γ przy braku materiału osłabiającego,

μ = (0,1071 ± 0,0011) - wartość podana przez komputer,

x - grubość absorbentu,

N₀ - liczba zliczeń wyładowań gamma przy określonej grubości absorbentu z ołowiu.

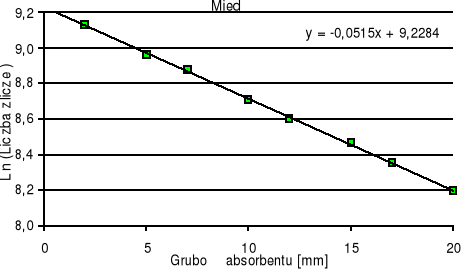
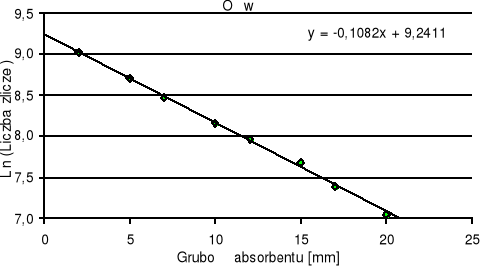
Wykres 2. Zależność wykładnicza liczby zliczeń N od grubości absorbenta x.

2. Do wyznaczenia współczynnika μ wykorzystaliśmy metodę najmniejszych kwadratów.

Po zlogarytmowaniu stronami równania:

N = N₀ *e^-μx

otrzymamy:

ln N = ln N₀ - μ*x

Wprowadzając oznaczenia a = -μ, b = ln N₀, y = ln N otrzymamy równanie prostej y = ax + b.

Według tej metody obliczamy współczynniki dla:

• Ołowiu Pb

Obliczenia upraszczamy obliczając mianownik:

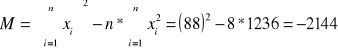
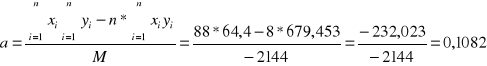
Stąd: μ = (- 0,1082 ± 0,0014) [cm^-1]

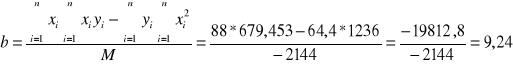
Wprowadzając oznaczenie D obliczamy odchylenie standardowe średniej:

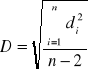
8. Analiza błędów.

Błędy x wyliczyliśmy korzystając ze wzorów na średnią arytmetyczną i odchylenie standardowe średniej.

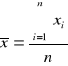
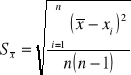
Podajemy wyliczenie błędu grubości dla jednej wielkości gdyż pozostałe zostały policzone w ten sam sposób w programie Exel i podane są w tabeli 3.

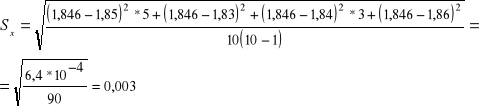
Tabela 3. Zestawienie wartości pomiarów grubości absorbentów ołowianych i ich błędów.

Lp.	1	2	3	4	5	6	7	8	9	10	Średnia	błąd x
20	19,95	19,96	19,94	19,97	19,97	19,96	19,96	19,95	19,94	19,93	19,953	0,004
17	16,92	16,90	16,91	16,92	16,92	16,91	16,90	16,90	16,90	16,92	16,910	0,003
15	14,82	14,85	14,84	14,85	14,84	14,85	14,86	14,84	14,82	14,83	14,840	0,004
12	11,88	11,90	11,91	11,89	11,89	11,89	11,90	11,91	11,89	11,89	11,895	0,003
10	9,98	9,97	9,99	9,98	9,97	9,96	9,98	9,97	9,98	9,98	9,976	0,003
7	6,96	6,95	6,94	6,94	6,95	6,96	6,96	6,95	6,94	6,95	6,950	0,003
5	5,05	5,04	5,05	5,04	5,01	5,03	5,04	5,04	5,04	5,03	5,037	0,004
2	1,85	1,85	1,83	1,84	1,84	1,84	1,85	1,85	1,86	1,85	1,846	0,003

Błędy N(x) liczyliśmy korzystając z różniczki logarytmicznej:

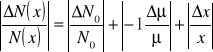
Podajemy wyliczenie błędu N(x) dla jednej wielkości gdyż pozostałe zostały policzone w ten sam sposób w programie Exel i podane są w tabeli 4.

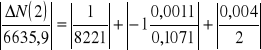
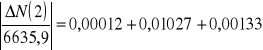
Tabela 4. Zestawienie obliczeń błędów dla N(x)

x	N	N0	ΔN0 / N0	Δμ / μ	Δx / x	Suma	ΔN0 [imp/min]
2	6635,9	8221	0,00012	0,01027	0,00133	0,01173	77,8
5	3504,1	5986	0,00017	0,01027	0,00073	0,01117	39,1
7	2258,1	4779	0,00021	0,01027	0,00037	0,01085	24,5
10	1199,0	3499	0,00029	0,01027	0,00027	0,01082	13,0
12	791,6	2862	0,00035	0,01027	0,00026	0,01088	8,6
15	431,5	2151	0,00046	0,01027	0,00028	0,01102	4,8
17	260,5	1609	0,00062	0,01027	0,00018	0,01107	2,9
20	134,7	1147	0,00087	0,01027	0,00021	0,01135	1,5

4

1

---