INTERPOLACJA:

Dana jest funkcja y = f (x),
, dla której znana jest tablica wartości w punktach zwanych węzłami interpolacji. Należy wyznaczyć taką funkcję W(x), aby:

W(x₀) = Y₀, W(x₁) = Y₁, ..., W(x_n) = Y_n

interpolacja funkcji f(x)

Zadaniem interpolacji jest wyznaczenie przybliżonych wartości funkcji zwanej funkcją interpolową w punktach nie będących węzłami interpolacji. Przybliżoną wartość funkcji obliczamy za pomocą funkcji zwanej funkcją interpolującą, która w węzłach ma te same wartości co funkcja interpolowana.

Interpolacja wielomianowa

W praktyce często używa się bazy złożonej z jednomianów

Wielomian interpolacyjny ma w tym przypadku postać:

dodatkowo musi być spełniony warunek:

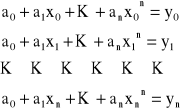
Powyższy układ równań ma jedyne rozwiązanie względem a₁, jeżeli wartości x₀, x₁, ..., x_n są od siebie różne

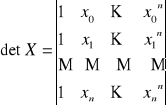
Macierz X^-1 dla bazy wielomianowej
nazywana jest macierzą Lagrange'a

Interpolacja Lagrange'a

W interpolacji wielomianowej Lagrange'a dla n+1 węzłów interpolacji

przyjmuje się funkcje bazowe w postaci

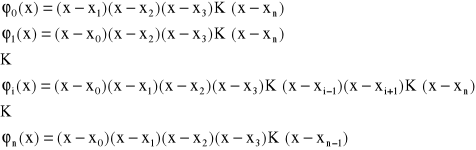
Funkcje te są wielomianami stopnia n zbudowanymi w ten sposób, że w funkcji bazowej φ₁ brakuje czynnika (x-x_i). Zatem wielomian interpolacji wyraża się następującym wzorem:

współczynniki a₀ ... a_n tego wielomianu wyznaczamy z równania:

X · A = Y, przy czym macierz X ma postać:

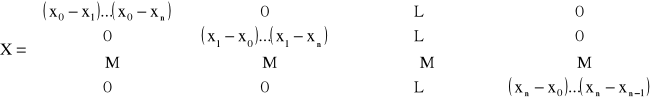
Macierz posiada tylko główną przekątną niezerową w związku z tym układ równań X · A = Y rozwiązuje się natychmiastowo

Można więc wielomian interpolacyjny Lagrange'a zapisać w postaci ułamka:

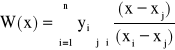
, j = 0, 1, ..., n

Przykład:

Wyznaczyć wielomian interpolacyjny Lagrange'a funkcji f (x) = e^x w przedziale [0,2 ; 0,5] mając dane:

f (0,2) = 1,2214, f (0,4) = 1,4918, f (0,5) = 1,6487

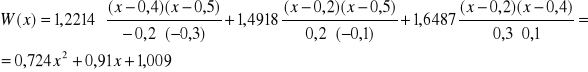
APROKSYMACJA

jest to przybliżanie funkcji f(x) zwanej aproksymowaną inną funkcją Q(x) zwaną funkcją aproksymującą. Aproksymacja bardzo często występuje w dwóch przypadkach:

• gdy funkcja aproksymowana jest przedstawiona w postaci tablicy wartości i poszukujemy dla niej odpowiedniej funkcji ciągłej

• gdy funkcję o dosyć skomplikowanym zapisie analitycznym chcemy przedstawić w „prostszej” postaci

Dokonując aproksymacji funkcji f(x) musimy rozwiązać dwa ważne problemy:

• dobór odpowiedniej funkcji aproksymującej Q(x)

• określenie dokładności dokonanej aproksymacji

Dobór odpowiedniej funkcji aproksymującej Q(x)

Najczęściej stosowane funkcje aproksymujące są dobierane w postaci wielomianów uogólnionych będących kombinacją liniową funkcji q(x)

Aproksymacja średniokwadratowa

Poszukujemy takiej funkcji Q(x) przybliżającej daną funkcję f(x), która umożliwi wygładzenie funkcji f(x), czyli pozwoli z zakłóconych błędami danymi wartości funkcji przybliżonej otrzymać gładką funkcję przybliżającą.

Funkcja przybliżająca ma postać

Przy czym współczynniki a_i są tak określone, aby wyrażenie było minimalne.

dla i=0, 1, ..., n

Aby wyznaczyć współczynniki a_i oznaczamy odchylenie

gdzie R_j jest odchyleniem w punkcie x_j.

Następnie obliczamy pochodne cząstkowe funkcji H względem a_i. Z warunku

, gdzie k = 0, 1, ..., n

otrzymujemy układ m+1 równań o niewiadomych a_i zwany układem normalnym

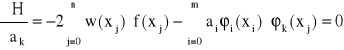
, gdzie k = 0, 1, ..., n

w zapisie macierzowym układ przyjmuje postać

gdzie

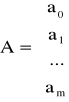
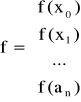
Aproksymacja wielomianowa

Jeżeli za funkcje bazowe przyjmiemy ciąg jednomianów (xⁱ), i = 0, 1, ..., n to układ normalny przyjmuje postać

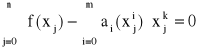
, k = 0, 1, ..., n

co po zmianie kolejności sumowania daje

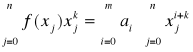
UKŁADY RÓWNAŃ LINIOWYCH

Rozpatrujemy układ n równań liniowych zawierających n niewiadomych

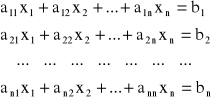
Układ ten można zapisać także w postaci macierzowej A · X = B, gdzie

metody dokładne: metoda Cramera, metoda eliminacji Gaussa, metoda Crouta (LU)

metody niedokładne: iteracja prosta, Gaussa-Siedla, metoda sukcesywnej nadrelaksacji (SOR)

Metody dokladne

1) Wzory Cramera

Jesli oznaczymy symbolem W wyznacznik główny układu równań

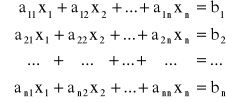
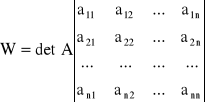
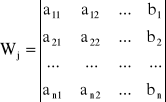
to można wykazać, że
, W ≠ 0, j = 1, 2, ..., n

Metoda ta należy do metod dokładnych. Ze względu na dużą złożoność obliczeniową praktycznie stosowana do numerycznego rozwiązywania równań.

2) Metoda eliminacji Gaussa

Metoda polega na zapisaniu układu równań w postaci macierzy C, której n pierwszych kolumn zawiera elementy a_ij macierzy głównej A, natomiast kolumnę n+1 tworzą dowolne wyrazy b_i.

Za pomocą wzorów określających nowe współczynniki

i=2,3,...,n j=2,3,...,n+1

W wyniku otrzymujemy układ:

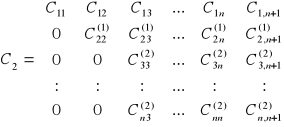
A nowe współczynniki wyrażone są wzorami

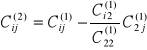
i=3, 4, ..., n j=3, 4, ..., n

Kontynuując takie postępowanie po wykonaniu n kroków dochodzimy do układu trójkątnego

Metody niedokładne (iteracyjne)

1) Metoda iteracji prostej (Jakobiego):

Metoda ta dla równania X=W*X+Z polega na przyjęciu zerowego przybliżenia wektora X=X^o, a następnie przeprowadzenia obliczeń iteracyjnych za pomocą zależności:

Xⁱ⁺¹=W*Xⁱ+Z i=0,1,...

Liczba kroków, które należy wykonać, aby uzyskać wymaganą dokładność rozwiązania, jest z reguły dość duża i istotnie zależy od przyjęcia punktu startowego X^o.

2) Metoda Gaussa-Seidla

Stanowi ulepszenie metody iteracyjnej prostej polegające na wykorzystaniu obliczonych k pierwszych składowych wektora Xⁱ⁺¹ do obliczenia składowej k+1. Modyfikacja ta znacznie przyspiesza proces obliczania.

3) Metoda sukcesywnej nadrelaksacji (SOR)

Jest ulepszeniem metody Gaussa-Seidla mającym poprawić szybkość zbieżności procesu iteracyjnego. Istota polega na sukcesywnym wprowadzaniu w miejsce składowych u_i po prawej stronie układu wartości

x_i + α (u_i - x_i) α - współczynnik nadrelaksacji, α∈<1,2>

UKŁADY RÓWNAŃ NIELINIOWYCH

1) Metoda Newtona

Dany jest układ równań nieliniowych z n niewiadomymi

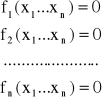
który możemy zapisać w postaci wektorowej f(x)=0

gdzie:

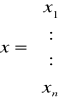
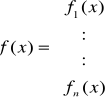
f(x) mają ciągłe pochodne pierwszego rzędu w otoczeniu pierwiastka.

pierwiastka równania

a = x^(k) + ε^(k)

gdzie x^(k) = {x₁^(k), ..., x_n^(k)} - k-tym przybliżeniem pierwiastka

jest błędem pierwiastka przybliżonego

Zastępując błąd
przyrostem
otrzymujemy równanie liniowe:

2) Metoda iteracji

Dany jest układ równań nieliniowych z n niewiadomymi

który możemy zapisać w postaci wektorowej

x=g(x)

gdzie:

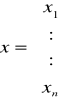
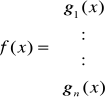
Zakładamy, że funkcja g₁, g₂, ..., g_n są rzeczywiste i ciągłe w pewnym otoczeniu odosobnionego pierwiastka a = {a₁, ..., a_n} układu równań.

Metoda iteracji polega na stosowaniu następującego wzoru

x^k+1 = g(x^(k))

Po przyjęciu przybliżenia
, w rezultacie otrzymujemy ciąg kolejnych przybliżeń
pierwiastka a równania.

3) Metoda siecznych

Rozpatrujemy układ równań nieliniowych w postaci

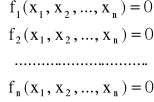
Który możemy ogólnie zapisać w postaci:

f(x)=0

gdzie x jest wektorem n zmiennych.

Metoda iteracji polega na stosowaniu wzoru wyliczającego k-te przybliżenie i-tej zmiennej tych:

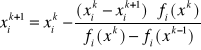
KWADRATURY GAUSSA

dobierają takie węzły, aby osiągnąć optymalne przybliżenie całki:

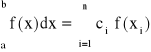
Węzły kwadratury x₁, x₂,..., x_n z przedziału całkowania [a,b] oraz współczynniki c₁, c₂,...,c_n są tak dobrane, aby zminimalizować błąd przybliżenia. Nie zakładamy jednak żadnych ograniczeń na węzły x_i o współczynnikach c_i natomiast chcemy zmaksymalizować rząd kwadratury.

METODA EULERA

ω_i+1=ω_i+hf(t_i, ω_i) (14)

Powyższy wzór nazywamy metodą Eulera - wzór ten nazywany jest inaczej równaniem różniczkowym, gdyż można zapisać:

(15)

Aby wyznaczyć wartość szukanej funkcji y(x) w następnym kroku h, wykorzystujemy poprzednią wartość funkcji oraz wielkości zmian funkcji - dzięki pochodnej. Natomiast uwzględniając błąd przybliżenia wzór (13) przyjmuje postać:

, gdzie
(16)

Lokalny błąd dyskretyzacji τ_i+1(h)

(17)

dodatkowo możemy określić krok h, dla którego błąd lokalny jest mniejszy od zadanej dokładności δ

, gdzie

Metoda Eulera - wstecz

Powyższe rozważania dotyczyły metody Eulera w przód, ponieważ krok spełniał warunek h>0. W analogiczny sposób można wyprowadzić metodą Eulera wstecz przyjmując h<0, wówczas otrzymujemy:

w_i+1 = w_i + hf (t_i+1, w_i+1) (22)

w_i+1^(k) = w_i + hf (t_i+1, w_i+1^(k-1)) (23)

Metoda wstecz różni się w stosunku do metody w przód argumentami funkcji f.

Metoda w przód wykorzystuje do obliczenia przybliżenia wartości z poprzedniego kroku, natomiast metoda wstecz jest równaniem uwikłanym, ponieważ aby obliczyć kolejne przybliżenie w_i+1 wykorzystujemy wartości z poprzedniego kroku oraz poszukiwaną wartość w_i+1. Takiego równania nie można rozwiązać w sposób

bezpośredni. Aby rozwiązać takie równanie (23) należy zastosować proces iteracyjny, czyli poszukujemy kilkakrotnie

w_i+1^(k), stojącej po prawej stronie równania podstawiając jako w_i+1^(k-1) - lewa strona równania, wynik przybliżenia z poprzedniej iteracji (k-1).

METODY RUNGEGO-KUTTY

Powszechnie na całym świecie stosuje się metody Rungego-Kutty czwartego rzędu. Polegają one na rozwiązaniu zagadnienia:

gdzie t∈ [a,b] oraz y(a)=α (25)

i przedstawieniu różnicy funkcji y(t) w punktach t_i+1 oraz t_i w postaci:

w_i+1 - w_i =
lub inaczej w_i+1 - w_i = h0 (t_i,w_i,h) (26)

gdzie m oznacza rząd metody, c_j są stałymi, a

gdzie α_j, β_j, γ_j, _δlj - stałe

h - krok całkowania

Określenie stałych c_j, α_j, β_j otrzymujemy poprzez rozwinięcie funkcji f(t,y) w szereg Taylora w otoczeniu punktu t_i

Metody R-K - metoda 2 rzędu

Metoda wyprowadzona przez rozwinięcie f(t,y) w szereg Taylora 2 rzędu pozwala określić stałe c₁, α₁,β₁, c₂, α₂, β₂ :

Metoda punktu środkowego:

C1 = 0 C2 = 1 α₁ = 0 α₂ = h/2 β1 = 0 β2 = ½ (28)

wówczas możemy zapisać:

k₁=hf (t_i,w_i) k₂=hf (t_i + ½ h, w_i + ½ k₁)

ostatecznie:

w_i+1=w_i+k₂

lub

w_i+1=w_i + hf(t_i + h/2, w_i + h/2 * f(t_i, w_i))

KWADRATURY NEWTINA-COTESA

Całkowanie z zastosowaniem kwadratur o ustalonych węzłach polega na zastąpieniu funkcji podcałkowej wielomianem interpolacyjnym Lagrange'a Li(x).

Jeżeli dla skończonego przedziału [a,b] wybierzemy zbiór punktów węzłowych {x₀, ..., x_n} takich, że:

x_i = x₀ + i · h

gdzie:

dla wówczas=(0, 1, …, n)

n - oznacza również stopień wielomianu interpolacyjnego

Oatecznie wzór kwadratury Newtona - Cotesa oraz reszta kwadratury

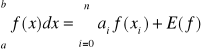
Kwadratury Newtona-Cotesa dają coraz lepszą dokładność wraz ze wzrostem n. Jednak wraz ze wzrostem n wzór na sumę posiada również rosnącą liczbę czynników. Dlatego kwadratur Newtona-Cotesa nie stosuje się dla dużych n

CAŁKA MONTE-CARLO

Mamy obliczyć przybliżoną wartość In całki oznaczonej

(129)

przy założenie, że f(x) jest funkcją ciągłą w przedziale domkniętym [a;b]

Następnie n-krotnie generujemy realizację x zmiennej losowej X o rozkładzie równomiernym w przedziale [a,b], otrzymujemy w rezultacie ciąg liczb x₁, x₂, ..., x_n,

Przybliżoną wartość całki określa wzór

8

---