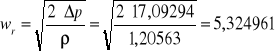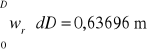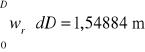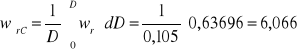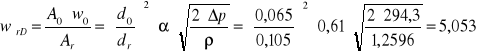Wydział Chemiczny |
Wyznaczanie profilu prędkości płynu w rurociągu o przekroju kołowym
Laboratorium inżynierii chemicznej
Grupa 2 |
(TCC3055l) |
Czwartek 8:15-11:00 |
Opracował: |
Dariusz Łozak |
Składowe |
Punktacja |
||
I |
Opracowanie arkusza wyników (schemat aparatury, metodyka badań, wyniki badań), oznaczenia |
(0-5), min. 2
|
|
II |
Przykład obliczeniowy |
(0-5), min. 3
|
|
III |
Wnioski |
(0-5), min. 2
|
|
∑ |
|
||
Punkty |
Ocena |
|
|
< 8 8 - 9 10 11-12 13 14 15 |
2.0 3.0 3.5 4.0 4.5 5.0 5.5 |
|
|
Wrocław, 06.06.2006
Oznaczenia
|
|
|
pole powierzchni otworu zwężki |
m2 |
|
|
|
|
pole powierzchni przekroju poprzecznego rurociągu |
m2 |
|
|
|
|
średnica otworu kryzy |
m |
|
|
|
|
średnica rurociągu |
m |
|
|
|
|
przyspieszenie ziemskie |
m/s2 |
|
|
|
|
w zależności od manometru - różnica poziomów cieczy manometrycznej lub poziom cieczy mikromanometrycznej |
m |
|
|
|
|
masa molowa powietrza |
kg/kmol |
|
|
|
|
ciśnienie |
Pa |
|
|
|
|
spadek ciśnienia |
Pa |
|
|
|
|
stała gazowa |
J/(kmol*K) |
|
|
|
|
odległość sondy od ścianki rurociągu |
m |
|
|
|
|
temperatura |
K |
|
|
|
|
prędkość powietrza w otworze kryzy |
m/s |
|
|
|
|
prędkość lokalna powietrza |
m/s |
|
|
|
|
prędkość średnia z całkowania graficznego |
m/s |
|
|
|
|
prędkość średnia ze spadku ciśnienia na zwężce |
m/s |
|
symbole greckie |
|
||||
|
|
|
współczynnik przepływu przez zwężkę |
- |
|
|
|
|
gęstość cieczy/gazu w określonej temperaturze |
kg/m3 |
|
indeksy dolne |
|
||||
|
CH3OH |
|
dotyczy metanolu |
|
|
|
H2O |
|
dotyczy wody |
|
|
1. Cel ćwiczenia
Celem ćwiczenia było wyznaczenie rozkładu prędkości gazu podczas przepływu przez rurę o przekroju kołowym, wyznaczenie średniej prędkości przepływu gazu na podstawie zmierzonych prędkości lokalnych oraz porównanie profilu uzyskanego na podstawie pomiaru lokalnych prędkości z profilem obliczonym za pomocą odpowiednich równań.
2. Aparatura
Schemat instalacji badawczej pokazano na rysunku 1 w załączniku A.
3. Metodyka badań
Badania zostały wykonane zgodnie z metodyką zawartą w załączniku A.
4. Wyniki badań
Wyniki badań zostały zgromadzone w tabeli 1 w załączniku A.
5 Metodyka obliczeń - przykład obliczeniowy
5.1 Obliczanie prędkości lokalnych wykonano następująco:
a) zmierzony spadek ciśnienia w mm CH3OH przeliczono na jednostki układu SI wg wzoru:
|
(1) |
b) gęstość powietrza dla temperatury pokojowej i ciśnienia atmosferycznego obliczam z przekształconego równania Clapeyrona:
|
(2) |
c) prędkości lokalne obliczono ze wzoru:
|
(3) |
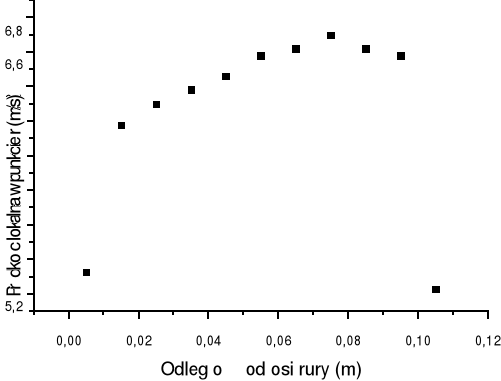
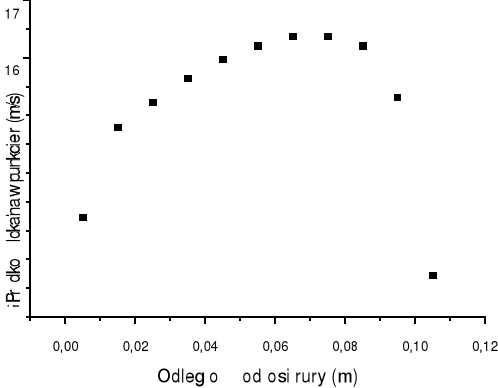
5.2 Obliczanie prędkości średniej za pomocą całkowania graficznego wykresu funkcji wr=f(D):
a) wykreślenie zmierzonego profilu prędkości powietrza w rurze i obliczenie pola powierzchni pod wykresami:
|
||
Rysunek |
1 |
Profil prędkości powietrza w rurze dla pierwszej serii pomiarowej
|
|
||
Rysunek |
2 |
Profil prędkości powietrza w rurze dla drugiej serii pomiarowej
|
b) prędkość średnią wyliczono na podstawie wzoru:
|
(4) |
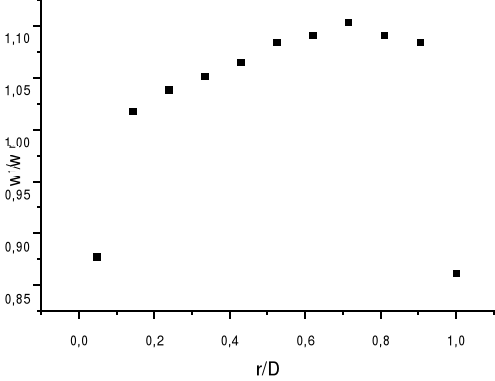
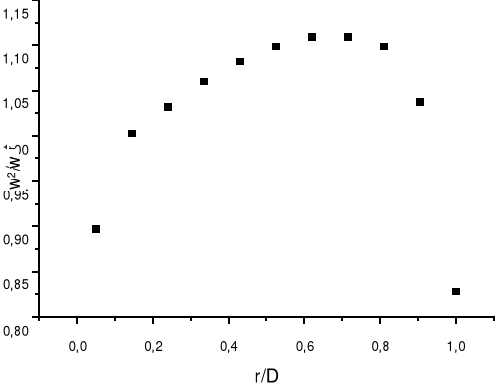
5.3 Wykreślenie profilu prędkości w układzie współrzędnych bezwymiarowych:
a) na podstawie obliczeń zależności wr/wśrC i r/D wyznaczono profil prędkości w postaci krzywej wr/wśrC=f(r/D):
|
||
Rysunek |
3 |
Profil prędkości powietrza w rurze w układzie współrzędnych bezwymiarowych dla większego natężenia przepływu (druga seria pomiarowa) |
|
||
Rysunek |
4 |
Profil prędkości powietrza w rurze w układzie współrzędnych bezwymiarowych dla mniejszego natężenia przepływu (pierwsz seria pomiarowa) |
5.4 Obliczam prędkości średnich na podstawie pomiarów spadku ciśnienia na kryzie pomiarowej:
a) zmierzony spadek ciśnienia w mm H2O przeliczono na jednostki układu SI wg wzoru:
|
(5) |
b) prędkość średnią obliczono na podstawie spadku ciśnienia na kryzie wg wzoru:
|
(6) |
Tabela |
1. |
Uzyskane wyniki obliczeń: |
||||||||
seria pomiarowa r [m] |
|
|
|
|
|
|
|
|||
0,005 |
105,6655 |
13,23959 |
14,751 |
0,897538 |
0,04762 |
1618,65 |
11,851 |
|||
0,015 |
132,0818 |
14,80231 |
|
1,003478 |
0,14286 |
|
|
|||
0,025 |
139,8514 |
15,23145 |
|
1,032571 |
0,23810 |
|
|
|||
0,035 |
147,6209 |
15,64883 |
|
1,060866 |
0,33333 |
|
|
|||
0,045 |
153,8365 |
15,97488 |
|
1,082969 |
0,42857 |
|
|
|||
0,055 |
158,4982 |
16,21512 |
|
1,099256 |
0,52381 |
|
|
|||
0,065 |
161,606 |
16,37332 |
|
1,10998 |
0,61905 |
|
|
|||
0,075 |
161,606 |
16,37332 |
|
1,10998 |
0,71429 |
|
|
|||
0,085 |
158,4982 |
16,21512 |
|
1,099256 |
0,80952 |
|
|
|||
0,095 |
141,4053 |
15,31584 |
|
1,038292 |
0,90476 |
|
|
|||
0,105 |
90,12643 |
12,2274 |
|
0,82892 |
1,00000 |
|
|
|||
0,005 |
17,0929 |
5,325 |
6,066 |
0,877837 |
0,04762 |
294,3 |
5,053 |
|||
0,015 |
22,9978 |
6,177 |
|
1,018236 |
0,14286 |
|
|
|||
0,025 |
23,9301 |
6,301 |
|
1,038671 |
0,23810 |
|
|
|||
0,035 |
24,5517 |
6,382 |
|
1,052074 |
0,33333 |
|
|
|||
0,045 |
25,1732 |
6,462 |
|
1,065308 |
0,42857 |
|
|
|||
0,055 |
26,1056 |
6,581 |
|
1,084857 |
0,52381 |
|
|
|||
0,065 |
26,4164 |
6,620 |
|
1,091295 |
0,61905 |
|
|
|||
0,075 |
27,0379 |
6,697 |
|
1,104059 |
0,71429 |
|
|
|||
0,085 |
26,4164 |
6,620 |
|
1,091295 |
0,80952 |
|
|
|||
0,095 |
26,1056 |
6,581 |
|
1,084857 |
0,90476 |
|
|
|||
0,105 |
16,4714 |
5,227 |
|
0,861729 |
1,00000 |
|
|
|||
6. Omówienie wyników, wnioski
6.1 Podstawy teoretyczne
Dla ustalonego, jednokierunkowego i uwarstwionego przepływu przez rurę o przekroju kołowym równanie Naviera-Stokesa upraszcza się do postaci zwyczajnego równania różniczkowego. W układzie współrzędnych cylindrycznych ma ono następującą formę:
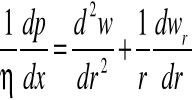
r- odl.od osi rury w kierunku normalnym [m
![]()
-prędkość lokalna w punkcie r, [m/s]
![]()
-lepkość dynamiczna
dp/dx-gradient ciśnienia wzdłuż osi rury, [Pa/m]
Scałkowanie tego równania pozwala uzyskać wrażenie na prędkość lokalną w dowolnym punkcie rury
![]()
gdzie: R- promień rury
Z tego równania wynikają związki między prędkością lokalną, maksymalną i średnią przepływającego płynu:
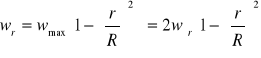
Wzrost prędkości cieczy powoduje przejście w obszar przepływu turbulentnego. Cząstki cieczy nie poruszają się już po torach równoległych do osi rurociągu, ale wykonują dodatkowe ruchy poprzeczne. Powstają wówczas wiry, które powodują spłaszczenie profilu. Wektory prędkości mają prawie jednakową wartość niemal w całym przekroju, a w cienkiej warstwie granicznej maleją liniowo do zera na ściance. Rozkład prędkości w przekroju poprzecznym podczas przepływu turbulentnego przestawia w przybliżeniu proste, ale niezbyt dokładne, równanie Kármána:
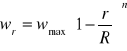
Wykładnik potęgowy n we wzorze jest funkcją liczby Reynoldsa. W warstwie granicznej w której występuje liniowy spadek prędkości, przepływ ma zawsze charakter laminarny. Tę cienką warstewkę przyścienną nazywa się warstewka Prandtla, a jej grubość dla przepływu turbulentnego wynosi 10-1 - 10-2 mm. Dla przepływu laminarnego jej grubość jest znacznie większa i równa się ok. 1mm.
Warstewka graniczna Prandltla odgrywa dużą rolę w procesach wymiany masy i ciepła, utrudniając ruch substancji i ciepła między ścianka a płynem wewnątrz rury czy aparatu. Rodzaj przepływu i warstewka graniczna ustalają się dopiero po pewnym odcinku rozbiegowym od wylotu płynu do rury, czy też za kolankiem rurociągu.
Jeżeli przepływający płyn jest ogrzewany lub chłodzony , to rozkład prędkości ulega pewnemu zniekształceniu. Zmiana kształtu rozkładu prędkości przy stałym natężeniu przepływu jest związana ze zmianą lepkości płynu. Jeżeli podczas chłodzenia zwiększy się lepkość płynu, to przy ścianie poruszać się on będzie wolniej, a w osi szybciej. Podczas ogrzewania relacje te układają się odwrotnie.
Kształty profilów prędkości przepływu płynu w rurze są różne dla przepływy laminarnego i burzliwego (turbulentnego). W ruchu laminarnym rozkład prędkości w(r) przepływy płynu lepkiego i nieściśliwego przez rurę cylindryczną ma postać wyżej wymienionego równania Hagena-Poiseuile'a z którego wynika, że rozkład prędkości jest paraboliczny:
![]()
gdzie: Δp - spadek ciśnienia na długości dx,
η - dynamiczny współczynnik lepkości,
R - promień wewnętrzny rurociągu,
r - odległość sondy pomiarowej od ściany rurociągu.
W praktyce występują głównie przepływy burzliwe. W polu prędkości płynu przy tego rodzaju przepływie w rurze można wyróżnić trzy obszary: rdzeń turbulentny będący zasadniczą częścią pola przekroju przepływu, podwarstwa laminarna - cienka warstewka przepływu laminarnego znajdująca się w pobliżu ścianek i strefa przejściowa znajdująca się pomiędzy wyżej wymienionymi. W podwarstwie laminarnej występuje duży gradient prędkości, z czym związane są naprężenia styczne w płynie. Natomiast w rdzeniu turbulentnym w skutek występowania ruchów wywołujących intensywną wymianę pędu między poruszającymi się z dużą prędkością elementami płynu, pojawiają się naprężenia turbulentne, których wartość jest w stosunku do wartości naprężeń w warstwie laminarnej jest znacznie wyższa. Dlatego też o naprężeniach w płynie w podwarstwie laminarnej decydują naprężenia związane z lepkością a w rdzeniu turbulentnym związane z naprężeniami turbulentnymi.
Takie własności przepływu mają wpływ na kształt profilu przepływu cieczy lub gazu w rurociągu o przekroju kołowym.
6.2 Wyniki doświadczalne
Na podstawie danych doświadczalnych wyznaczyłem profile prędkości powietrza w rurze o przekroju kołowym. Z wykonanych obliczeń można określić na podstawie pomiaru lokalnych prędkości poszczególne profile przepływów. Dla ruchu burzliwego profil ma postać spłaszczoną, prędkość jest równomierna w całym czole, natomiast w ruchu laminarnym występuje postać paraboli największa szybkość występuje w środkowej części rurociągu. Profile ukazane na wykresach są w porównaniu z teoretycznymi bardzo przybliżone. W szczególności, jeśli chodzi o przepływ laminarny, pewne niedoskonałości uwidaczniają się przy przepływie burzliwym, gdzie nie ma ustabilizowania się czoła. Średnie prędkości wyznaczone na podstawie całkowania graficznego profilu prędkości różnią się od prędkości średnich wyznaczonych na kryzie pomiarowej, jednak nie są to różnice wielkie. Wynoszą odpowiednio dla ruchu laminarnego +/-1 oraz dla burzliwego więcej +/-3 a więc w przepływie o małym natężeniu ta różnica jest niewielka, natomiast w przepływie o dużym natężeniu różnica jest znaczna. Reasumując wnioskuję, że na wyznaczenie profili mogła mieć wpływ aparatura. Jak już wcześniej wspominałem różnią się one od wyznaczonych teoretycznie profili, jednak te różnice nie są wielkie.
0
8
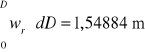
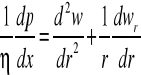
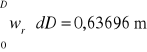
![]()
F,L
Wyszukiwarka
Podobne podstrony:
Wyznaczanie profilu prdkoci płynu w rurociągu o przekroju kołowym, Studia, inżynieria chemiczna spra
prędkości płynu, Studia, inżynieria chemiczna sprawozdania, wyznaczanie profilu prędkości płynu w ru
Wyznaczanie profilu prędkości płynu w rurociągu o przekroju kołowym, pwr biotechnologia(I stopień),
Wyznaczanie profilu prędkości płynu w rurociągu o przekroju kołowym
Wyznaczanie profilu prędkości płynu w rurociągu o przekroju kołowym
Wyznaczanie profilu prędkości płynu w rurociągu o przekroju kołowym
Wyznaczanie profilu prędkości przepływu w przewodzie o przekroju kołowym
WYZNACZANIE PROFILU PRĘDKOŚCI PŁYNU
1 WYZNACZANIE STRAT CISNIENIA PODCZAS PRZEPŁYWU PŁYNU W RUROCIĄGU
1 WYZNACZANIE STRAT CISNIENIA PODCZAS PRZEPŁYWU PŁYNU W RUROCIĄGU
1 WYZNACZANIE STRAT CISNIENIA PODCZAS PRZEPŁYWU PŁYNU W RUROCIĄGU
śródka, wytrzymałość materiałów,Skręcanie prętów o przekroju kołowym
[10]Tarcie cięgien opasujących walec o przekroju kołowym, [10] Tarcie cięgien opasujących walec o p
[10]Tarcie cięgien opasujących walec o przekroju kołowym, [10] Tarcie cięgien opasujących walec o p
BN 8971 07 1986 Prefabrykaty budowlane betonu Rury cisnieniowe o przekroju kolowym BETRAS
wyznaczenie profilu predkości, mechanika plynów
Dobór przekroju przewodów, Dokumenty(1)
03 elementy o przekroju kolowym
Wyznaczanie rozkładu naprężeń normalnych i stycznych w przekroju belki zginanej, Budownictwo PCz, Wy
więcej podobnych podstron