TERMODYNAMIKA

I TEORIA KINETYCZNA

• Prawa mechaniki opisywały znakomicie proste układy kilku ciał. W gazach typowa objętość zawiera ogromne (liczba Avogadro:
) ilości cząsteczek, więc opis czysto „mechaniczny” trudno do nich stosować.

• Istnieją pewne wielkości (parametry) makroskopowe, które zadowalająco opiszą skomplikowany układ cząsteczek gazu: ciśnienie, objętość, temperatura. Badaniem związków między nimi zajmuje się termodynamika.

• Istnieje też możliwość „powrotu” do podejścia mikroskopowego i wyprowadzenia w jego ramach zależności między parametrami termodynamicznymi. Takie podejście oferuje teoria kinetyczna.

CIŚNIENIE

• Ciśnienie definiujemy jako stosunek siły, jaką gaz (ciecz) wywiera na ściankę naczynia, w którym się znajduje, do powierzchni tej ścianki:

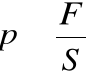
Jednostką ciśnienia jest Pascal [Pa].

• Można też mówić o ciśnieniu wewnętrznym cieczy, czyli sile, jaką oddziaływają na siebie poszczególne elementy objętości cieczy. Ciśnienie to jest jednakowe w całej objętości płynu. Prawo Pascala mówi, że ciśnienie, wywierane na część powierzchni płynu rozchodzi się jednakowo na wszystkie części powierzchni ograniczającej płyn.

• Prawami, opisującymi statyczne zależności między ciśnieniami w cieczach zajmuje się hydrostatyka - choć w zasadzie przedrostek „hydro” powinien wskazywać tylko na wodę...

PRAWO PASCALA

• Prawo Pascala w obecności sił ciężkości dla cieczy nieściśliwej przybiera ogólniejszą postać:

gdzie
jest ciśnieniem zewnętrznym przyłożonym do górnej powierzchni cieczy,
jest gęstością cieczy a
odległością od górnej powierzchni (
to oczywiście przyspieszenie ziemskie).

Równanie to nie zależy od kształtu naczynia.

• Również atmosfera ziemska wywiera na ciała, znajdujące się przy powierzchni Ziemi, ciśnienie, „wynikające” z członu
. Wynik liczbowy dla atmosfery Ziemi:

(Otrzymujemy go po uwzględnieniu średniej gęstości atmosfery).

BAROMETRY, POMPY WODNE

• Praktycznym zastosowaniem prawa Pascala jest wykorzystanie go do budowy barometrów - przyrządów, służących do pomiarów ciśnienia.

Ciśnienie na powierzchni „swobodnej” cieczy musi być takie samo, jak ciśnienie słupa cieczy w rurce.

Wysokość słupa rtęci dla ciśnienia normalnego:

Wysokość odpowiedniego słupa wody:

• Pompy próżniowe do wydobywania wody ze studni głębinowych - maksymalna głębokość pompowania 10,3 m... (chyba, że zastosować specjalne układy kilku pomp, zanurzonych w cieczy).

PRAWO ARCHIMEDESA

• Zgodnie z prawem Pascala, jeśli zanurzymy w cieczy ciało stałe, to na poszczególne części tego ciała będzie działać różne ciśnienie, w zależności od tego, na jakiej głębokości znajduje się dana cześć tego ciała:

Siła wypadkowa (nazywana siłą wyporu)

gdzie
jest masą cieczy, wypartą przez to ciało.

• Prawo Archimedesa mówi, że na ciało zanurzone w cieczy działa siła wyporu, skierowana przeciwnie do siły ciężkości, równa liczbowo ciężarowi wypartej cieczy.

PRAWO GAZÓW DOSKONAŁYCH

• Przez gaz doskonały rozumiemy gaz, który spełnia następujące warunki:

1. objętość cząsteczek jest o wiele mniejsza niż objętość, zajmowana przez gaz;

2. zasięg sił, działających między dwiema cząsteczkami, jest o wiele mniejszy, niż średnia odległość między nimi.

Gaz doskonały jest to więc zbiór „małych, twardych kulek”, które sprężyście zderzają się ze sobą i ze ściankami ograniczającego go naczynia.

• W termodynamice podstawowym prawem, rządzącym zachowaniem gazu doskonałego, jest prawo gazów doskonałych (prawo Clapyerona):

gdzie
jest ciśnieniem,
- objętością gazu,
- jego temperaturą,
- liczbą cząsteczek gazu w jednostce objętości a
pewną uniwersalną stałą fizyczną, taką samą dla wszystkich gazów.

PRAWO GAZÓW DOSKONAŁYCH - c.d.

• Aby wyprowadzić prawo gazów doskonałych w ramach teorii kinetycznej, rozważmy pudełko o objętości
, w którym zamknięto
cząsteczek gazu - małych, twardych kulek...

• Średnia siła, którą cząsteczka wywiera w trakcie zderzenia ze ścianką „x” w czasie Δt:

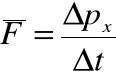
• Zmiana pędu spowodowana zderzeniem ze ścianką:

• Czas między kolejnymi zderzeniami z tą ścianką:

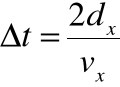
PRAWO GAZÓW DOSKONAŁYCH - c.d.

• Średnia siła, działająca na ściankę ze strony każdej cząstki:

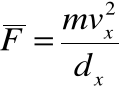
• Całkowita średnia siła od wszystkich
cząsteczek:

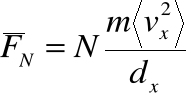
gdzie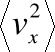
jest średnią kwadratu prędkości w kierunku x.

• Dzieląc przez pole ścianki
i zastępując
przez objętość naczynia
, otrzymujemy wzór na średnie ciśnienie:

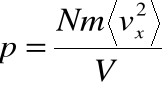
PRAWO GAZÓW DOSKONAŁYCH - c.d.

• Uogólniając na trzy wymiary, zauważmy, że:

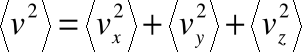
a ponieważ w przypadku wartości średnich: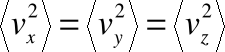

więc ostatecznie:

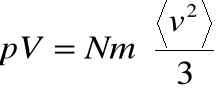
Wynik ten zwany jest prawem Boyle'a (iloczyn
jest stały dla danego gazu tak długo, póki stała jest energia kinetyczna jego cząstek).

• Żeby podany powyżej związek był zgodny z klasycznym, termodynamicznym prawem gazów doskonałych, prawa strona równania, niewątpliwie związana z energią kinetyczną cząstki, musi zawierać kinetyczną definicję temperatury bezwzględnej.

TEMPERATURA

• Temperatura definiowana w ramach termodynamiki klasycznej (makroskopowej), to parametr opisujący stan równowagi termodynamicznej układu.

• W teorii kinetycznej zdefiniujemy temperaturę jako:

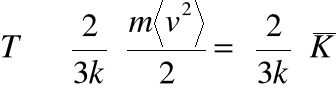
gdzie
jest średnią energią kinetyczną przypadającą na 1 cząsteczkę gazu.

• Współczynnik proporcjonalności w powyższej definicji zawiera wielkość
, zwaną stałą Boltzmanna, która została zdefiniowana poprzez wyznaczenie 100-stopniowej skali temperatury, opartej na punktach zamarzania i wrzenia wody:

• Dla tak zdefiniowanej temperatury, oba prawa gazów doskonałych (termodynamiczne i w teorii kinetycznej) są równoważne.

TEMPERATURA

• Bezwzględna skala temperatur - skala Kelvina - oparta jest na definicji punktu „0” jako „zera” energii kinetycznej, kiedy ustaje wszelki ruch cząsteczek, i jednostce temperatury - kelwinie (K) - równym stopniowi Celsjusza. „Zero bezwzględne” to ok. -273 stopnie w bardziej znanej na co dzień skali Celsjusza.

• Skala Celsjusza została stworzona na bazie dwóch punktów, charakterystycznych dla wody: temperaturze zamarzania (przyjętej za „0”) i temperaturze wrzenia (jako „100”). Jednostką jest więc
tego przedziału, zwana stopniem Celsjusza (°C).

• W krajach anglosaskich powszechnie używana jest skala Fahrenheita - jeden stopień tej skali równa się
stopnia Celsjusza.

• Inne spotykane skale temperatur - Reaumura, Rankine'a - mają już dziś tylko znaczenie historyczne.

Celsius in Fahrenheit :		Celsius * 1.8 + 32
Celsius in Kelvin :		Celsius + 273.15
Celsius in Rankine :		Celsius *1.8 + 491.67
Celsius in Reaumur :		Celsius * 0.8
Fahrenheit in Celsius :		( Fahrenheit - 32 ) * (5/9)
Fahrenheit in Kelvin :		( Fahrenheit - 32 ) * (5/9) + 273.15
Fahrenheit in Rankine :		Fahrenheit + 459.67
Fahrenheit in Reaumur :		( Fahrenheit - 32 ) * (4/9)
Kelvin in Celsius :		Kelvin - 273.15
Kelvin in Fahrenheit :		( Kelvin - 273.15 ) * 1.8 + 32
Kelvin in Rankine :		Kelvin * 1.8
Kelvin in Reaumur :		( Kelvin - 273.15 ) * 0.8
Rankine in Celsius :		( Rankine * (5/9) ) - 273.15
Rankine in Fahrenheit :		Rankine - 459.67
Rankine in Kelvin :		Rankine * ( 5/9)
Rankine in Reaumur :		( Rankine * (4/9) ) - 218.52
Reaumur in Celsius :		Reaumur * 1.25
Reaumur in Fahrenheit :		Reaumur * 2.25 + 32
Reaumur in Kelvin :		Reaumur * 1.25 + 273.15
Reaumur in Rankine :		Reaumur * 2.25 + 491.67

TERMOMETRY

• Mikroskopowa definicja temperatury (miara średniej energii kinetycznej cząsteczek) nie nadaje się do pomiarów. Pod tym względem lepsza jest definicja makroskopowa, wiążąca inne, mierzalne parametry gazu doskonałego - ciśnienie i objętość - z szukaną temperaturą.

• Termometry „objętościowe” związane są ze zmianą wymiarów ciała ze zmianą temperatury (rozszerzalność liniowa).

Najprostszym przykładem jest termometr rtęciowy. Dokładniejszym przyrządem tego typu jest termometry gazowy stałego ciśnienia. Pomiar temperatury polega na pomiarze objętości (wymiaru liniowego) rozszerzającego się ośrodka.

• Termometry gazowe stałej objętości bazują na pomiarze zmian ciśnienia ze zmianą temperatury.

Służą do pomiarów małych temperatur.

• Termorezysty - to elementy elektryczne, które mierzą zmiany temperatury poprzez pomiar związanej z nią zmiany oporu przewodnika bądź półprzewodnika.

TERMOMETRY - c.d.

• Termopary to układy dwóch przewodników, na stykach których wytwarza się napięcie termoelektryczne, proporcjonalne do różnicy temperatur obu styków.

• Pirometry mierzą temperaturę poprzez pomiar (porównanie) emisji promieniowania ciała, którego temperaturę chcemy określić, z emisją ciała doskonale czarnego - nadają się do pomiaru wysokich temperatur i do pomiarów „na odległość”.

• Bolometry również bazują na fakcie, że emisja promieniowania danego ciała jest proporcjonalna do jego temperatury.

• Układy bimetali służą raczej jako dwustanowe przełączniki termiczne, niż termometry, ale też pełnią rolę „mierników” temperatury.

• Budowa wszystkich tych urządzeń bazuje na zerowej zasadzie termodynamiki: jeżeli ciało 1 i ciało 2 znajdują się w równowadze termicznej i ciała 2 i 3 są również w takiej równowadze, to ciała 1 i 3 są także w tej samej równowadze termicznej w której byłyby, gdyby były w kontakcie ze sobą.

ROZKŁAD PRĘDKOŚCI CZĄSTECZEK

• Wyprowadzając podstawowe równanie kinetycznej teorii gazów wprowadziliśmy pojęcie średniej kwadratu prędkości (średniej prędkości kwadratowej), która charakteryzowała zbiór cząsteczek jako całość. Problemem pozostaje wyznaczenie tej średniej, czyli znalezienie formuły rozkładu prędkości cząsteczek gazu doskonałego.

• Maxwell rozwiązał teoretycznie to zagadnienie, podając prawo pozwalające określić, jaka liczba cząstek
z całej ilości
cząstek gazu doskonałego w jednostce objętości (
) ma w danej temperaturze prędkości w przedziale od
do
:

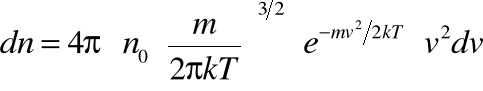
ROZKŁAD MAXWELLA

• Korzystając z rozkładu Maxwella można wyliczyć:

• prędkość najbardziej prawdopodobną:
  

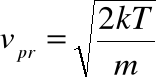
• prędkość średnią kwadratową:
  

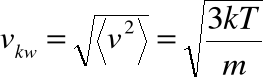
• prędkość średnią:
  

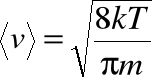
• Wraz ze wzrostem temperatury, krzywe przedstawiające rozkład prędkości cząsteczek gazu zmieniają się:

Maksimum krzywej przesuwa się wraz ze wzrostem temperatury w kierunku większych prędkości - przy ogrzewaniu gazu udział cząsteczek obdarzonych małymi prędkościami zmniejsza się.

WZÓR BAROMETRYCZNY

• Rozkład Maxwella jest prawem statystycznym, otrzymanym za pomocą metod rachunku prawdopodobieństwa - jest tym bardziej zgodny z rzeczywistością, im więcej cząstek gazu rozpatrujemy. Rozkład ten nie uwzględnia również działania zewnętrznego pola sił (np. grawitacji).

• Jeśli rozpatrzymy gaz w polu sił grawitacyjnych Ziemi, to uwzględnić trzeba zmiany ciśnienia zgodnie z prawem Pascala - ze wzrostem wysokości zmienia się ciśnienie gazu, a więc i jego koncentracja (liczba cząstek w jednostce objętości
). Z prawa Pascala i prawa gazu doskonałego możemy otrzymać tzw. wzór barometryczny:

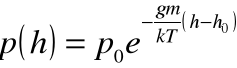
czyli wzór na ciśnienie
na wysokości
w zależności od temperatury gazu.

ŚREDNIA DROGA SWOBODNA

• Cząsteczki gazu mają skończone wymiary i stale zderzają się ze sobą (wymieniając się energią kinetyczną i pędami, stąd rozkład prędkości Maxwella!). Pomiędzy dwoma kolejnymi zderzeniami cząsteczki poruszają się prostoliniowo i jednostajnie a odległość przy tym przebywaną nazwiemy średnią długością drogi swobodnej
.

• Korzystając z rozkładu Maxwella, można pokazać, że średnia droga swobodna cząsteczki zależy od „wymiaru” cząsteczki
i liczby cząsteczek w jednostce objętości gazu
:

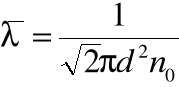
• Przy stałej temperaturze liczba cząsteczek w objętości gazu jest wprost proporcjonalna do ciśnienia gazu, więc średnia droga swobodna jest odwrotnie proporcjonalna do ciśnienia. A zatem:

p [mm Hg]	760	1	10^-2	10^-4	10^-6
[cm]

STOPNIE SWOBODY CZĄSTECZEK

• Liczba stopni swobody ciała to najmniejsza możliwa liczba współrzędnych (liczba współrzędnych niezależnych), które musimy podać, aby jednoznacznie określić położenie ciała w przestrzeni.

• Cząsteczki gazu jednoatomowego mają trzy stopnie swobody - ich położenie opisują trzy współrzędne, np. x,y,z układu kartezjańskiego.

• Cząsteczki dwuatomowe mają pięć stopni swobody - trzeba na przykład podać trzy współrzędne jednego atomu i dwie współrzędne, określające położenie drugiego atomu względem pierwszego (tylko dwie, bo stała odległość między nimi da nam automatycznie trzecią współrzędną!).

• Cząsteczki, zbudowane z większej ilości atomów bądź po prostu ciała sztywne (traktowane jako układ wielu atomów, o nie zmieniających się odległościach między nimi), maja sześć stopni swobody.

ZASADA EKWIPARTYCJI ENERGII

• Jednym z ważniejszych praw fizyki statystycznej jest prawo równomiernego rozkładu energii między stopnie swobody: na każdy stopień swobody cząsteczki średnio przypada jednakowa energia kinetyczna, równa
(zasada ekwipartycji energii).

• Jeżeli cząstka jest obdarzona
stopniami swobody, to jej średnia energia kinetyczna: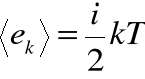

• W przypadku gazu doskonałego jedyną energią cząstek była energia kinetyczna. W przypadku np. ciał stałych należy uwzględniać również energię potencjalną oddziaływań międzycząsteczkowych. Można wykazać, że zasada ekwipartycji energii jest wtedy również słuszna, jeśli tylko energia potencjalna jest funkcją kwadratów współrzędnych cząsteczki.

Przykład: atomy cząsteczki dwuatomowej wykonują drgania harmoniczne wzdłuż prostej, łączącej je, czyli cząsteczka ta ma jeden stopień swobody ruchu drgającego. Średnia energia potencjalna tego układu jest więc równa:

.

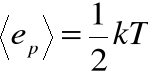
EKWIPARTYCJA ENERGII - c.d.

• W gazie doskonałym nie ma oddziaływań między cząsteczkami, więc energia potencjalna jest równa 0. Dlatego energia wewnętrzna 1 mola gazu doskonałego równa się sumie energii kinetycznych
(liczba Avogadro!) cząsteczek:

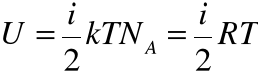
(R - stała gazowa). Energia ta zależy więc liniowo od temperatury T, co pozwala wprowadzić pojęcie temperatury jako miary energii wewnętrznej cząsteczek.

• W przypadku gazu rzeczywistego, w którym cząsteczki jednak oddziaływają ze sobą, istnieje energia potencjalna zależna od odległości między cząsteczkami, czyli od objętości właściwej gazu.

Energię tę można wyznaczyć, jeżeli znamy charakter wzajemnego oddziaływania między cząsteczkami, ale prawo równomiernego rozkładu energii nie umożliwi nam w tym przypadku wyznaczenia energii wewnętrznej takiego gazu.

INNE ROZKŁADY STATYSTYCZNE

• Rozkład Maxwella oraz zasadę ekwipartycji energii otrzymaliśmy przy następujących założeniach:

• spełnione są zasady zachowania (liczby cząsteczek, energii, pędu, momentu pędu, ładunku);

• wszystkie procesy fizyczne w układzie przebiegają w sposób ciągły w czasie i przestrzeni;

• obliczenia statystyczne przeprowadzono przy założeniu rozróżnialności cząstek; (por. kombinatoryka w rachunku prawdopodobieństwa);

• każda cząstka może mieć dowolne wartości współrzędnych i prędkości, niezależnie od wartości współrzędnych i prędkości innych cząstek; (a więc w szczególności prawdopodobieństwo znalezienia się cząstki w danej objętości przestrzeni jest niezależne od tego, ile innych cząstek tę „komórkę” przestrzeni zajmuje!).

Dwa pierwsze założenia są ogólnymi założeniami fizyki klasyczne. Dwa kolejne są specyficznymi założeniami klasycznej fizyki statystycznej.

INNE ROZKŁADY STATYSTYCZNE - c.d.

• W statystyce kwantowej uważa się za niemożliwe rozróżnienie dwóch takich samych cząsteczek (np. elektronów), a więc musimy znaleźć inną statystykę, niż Maxwella (zwany też rozkładem Maxwella -Boltzmanna).

• Innym postulatem mechaniki kwantowej jest szczególna właściwość mikrocząstek (np. elektronów), odróżniająca je od ciał makroskopowych - np. istnienie uniwersalnej stałej Plancka
, określającą między innymi skwantowaną energię cząstek i podobnie skwantowaną przestrzeń: elementarna objętość, w której znajdują się cząstki, nie może być mniejsza niż
(m - masa cząstki). Jeżeli założymy, że w takiej objętości może znajdować się dowolna liczba cząstek, to otrzymamy w efekcie kwantową statystykę Bosego-Einsteina. Jeżeli natomiast cząstki podlegają zakazowi Pauliego (max. dwie cząstki na objętość), to otrzymamy kwantową statystykę Fermiego-Diraca.

23

h

rtęć

próżnia

h

d

Pole S

F_{w dół}

F_{w górę}

y

x

z

v

v_x

Pole S

d_x

T₁

T₂

T₃

---