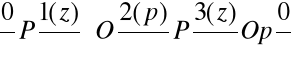Synteza strukturalna i geometryczna mechanizmu:

• Budowa łańcucha kinematycznego - schemat ideowy:

Symboliczny zapis struktury i parametrów mechanizmu przedstawia poniższa tabelka:

Zakres danych	Parametry mechanizmu
1.Struktura mechanizmu
2.Parametry kinematyczne członu napędzającego 1	(s1,v1,0)
3. Masy i momenty bezwładności członów (mi, JSi)	(0,0);(0,0);(m3,JS3)
4. Obciążenie uogólnionymi siłami zewnętrznymi (Pi, Mi)	(0,0);(0,0);(P3,M3)
5. Uogólniona siła równoważąca do wyznaczenia (PR1 lub MR1)	PR1

Na podstawie symbolicznego zapisu struktury i parametrów łańcucha kinematycznego budujemy schemat ideowy, który przedstawia rysunek poniżej:

• Ruchliwość i klasa mechanizmu:

Ruchliwość mechanizmu:

Ruchliwość obliczamy ze wzoru: w=3n-2p₅-p₄, gdzie:

w - ruchliwość, n - liczba członów, p₅ - liczba par kinematycznych klasy piątej, p₄ - liczba par kinematycznych klasy czwartej,

W naszym przypadku n=3, p₄=0, p₅=4. Więc ruchliwość wynosi:

w=3•3-2•4=1

Klasa mechanizmu:

Po odłączenie członu napędzającego 1, pozostałe człony 2 i 3 tworzą grupę strukturalną.

Ruchliwość grupy strukturalnej badamy po połączeniu jej członów ruchomych z podstawą (przedstawia to powyższy rysunek). W tym przypadku: n=2, p₄=0, p₅=3. Ruchliwość wynosi więc: w=3•2-2•3=0.

Grupa strukturalna (2,3) jest grupą klasy 2 postaci 3.

Analizowany mechanizm składa się z członu napędzającego 1 i grupy strukturalnej klasy 2, jest więc mechanizmem klasy 2.

Nazwa strukturalna mechanizmu: mechanizm jarzmowy.

• Ograniczenia geometryczne:

Mechanizm będzie działał prawidłowo, jeżeli spełniony (w każdym położeniu mechanizmu) będzie warunek:

• Model mechanizmu w programie SAM.

2. Analiza kinematyczna mechanizmu:

Do obliczeń kinematycznych przyjęto następujące dane:

s₁=0,2m=200mm , v₁=2 m/s = 2000 mm/s,

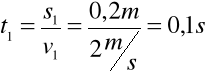
Obliczenie czasu t₁ wykonane jest w celu wprowadzenia prędkości v₁ w programie SAM. Wszystkie odczyty w tym programie będą dokonywane dla czasu t=0s.

Wymiary mechanizmu:

l_AB= 150mm= 0,15m

l_BC= 250m = 0,25m

l_CD= 80mm= 0,08m

l_CS3=170mm= 0,17m

• Analiza kinematyczna mechanizmu metodą grafoanalityczną:

Zadanie rozwiązujemy wykreślnie korzystając z programu AUTOCAD. W tym celu rysujemy mechanizm w zadanym położeniu. Podziałka rysunkowa mechanizmu:

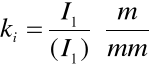
Analiza prędkości:

Przyjmujemy podziałkę prędkości:

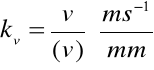
Analizę prędkości przeprowadzimy na podstawie równania:

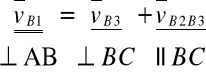
gdzie v_B1=v₁

Powyższe równanie rozwiązujemy wykreślnie, a następnie odczytujemy z rysunku wartości prędkości.

Plan prędkości:

Z planu prędkości odczytujemy:

v_B2B3 = 1600mm/s= 1,6 m/s

v_B2=1200mm/s= 1,2 m/s

Następnie obliczam prędkość kątową członu nr 3:

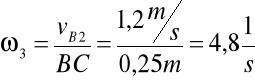
Obliczam ze wzorów prędkości punktów D oraz S3:

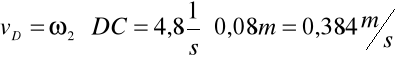
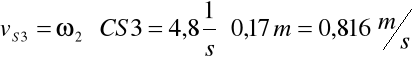
Analiza przyspieszeń:

Analizę przyspieszeń dokonujemy za pomocą równania:

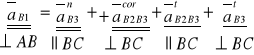
gdzie:

a_B1=0, bo v_B1=const.

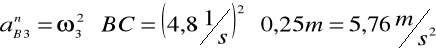
Plan przyspieszeń:

Z palnu przyspieszeń odczytujemy wartości:

Obliczam przyspieszenie kątowe członu nr 3:

Wyznaczam przyspieszenia punktu D:

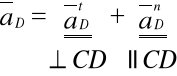
, przy czym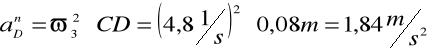
,

Z planu przyspieszeń odczytujemy:

a_D=5,253 m/s²

Wyznaczam przyspieszenie punktu S3:

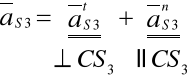
, przy czym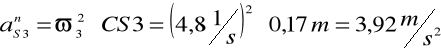
,

Z planu przyspieszeń odczytujemy:

a_S3=11,114 m/s²

• Analiza kinematyczna mechanizmu metodą analityczną:

Wielobok wektorowy mechanizmu:

Mamy cztery wektory, będziemy więc potrzebowali 2n-2 (gdzie n- liczba wektorów, w tym przypadku n=4) = 2*4-2=6 danych.

Dane: s₁,l₀, l₁, φ_s=180⁰, φ₀=0⁰, φ₁=90⁰

Szukane: φ_3, ω_3, v_B, v_D, v_S3, ε_3, a_B, a_D, a_S3

Mechanizm opisujemy wielobokiem wektorowym:

Zapisujemy rzuty wektorów na oś x i oś y:

Z pierwszego równania rzutów wektorów otrzymujemy:

Z drugiego równania rzutów wektorów otrzymujemy:

Następnie dzielimy je przez siebie:

Otrzymujemy wzór na obliczenie kąta φ₃:

Przy jego pomocy obliczam kąt φ₃ w zadanym położeniu mechanizmu:

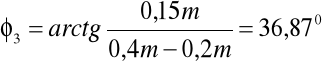
Długość członu l₃ znajdujemy ze wzoru:

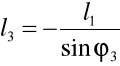
Obliczam długość członu l₃ mechanizmu w zadanym położeniu:

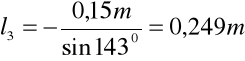
W celu znalezienia prędkości różniczkuję pierwsze z równań rzutów wektorów na osie:

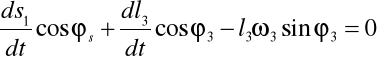
przy czym:

,
,

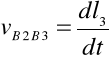
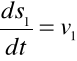
Aby znaleźć v_B2B3 obracamy układ współrzędnych o kąt φ₃:

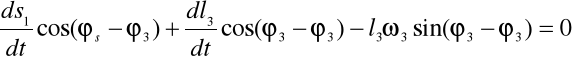
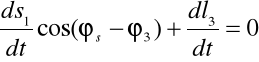
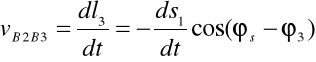
Obliczam v_B2B3 mechanizmu w zadanym położeniu:

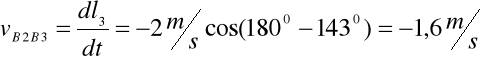
Aby znaleźć ω₃ obracamy układ współrzędnych o kąt (φ₃-90⁰):

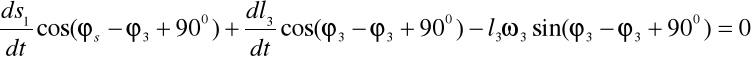
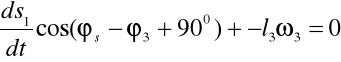
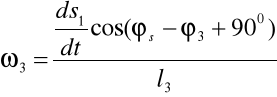
Obliczam ω₃ mechanizmu w zadanym położeniu:

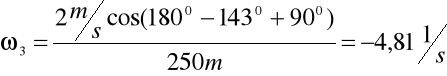
Obliczam prędkości punktów D i S3:

W celu znalezienia przyspieszeń różniczkuję równanie, z którego obliczałem prędkości:

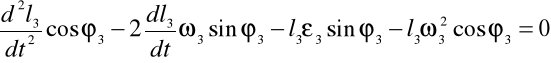
Aby znaleźć a^t_B2B3 obracam układ współrzędnych o kąt φ₃ i otrzymuję równanie:

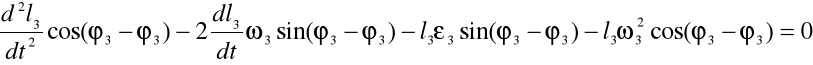
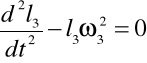
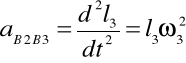
Obliczam a^t_B2B3 mechanizmu w zadanym położeniu:

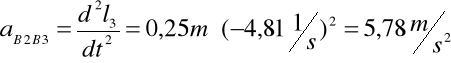
Aby znaleźć ε₃ obracam układ współrzędnych o kąt (φ₃-90⁰) i otrzymuję równanie:

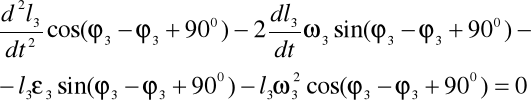
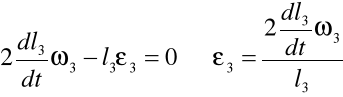
Obliczam ε₃ mechanizmu w zadanym położeniu:

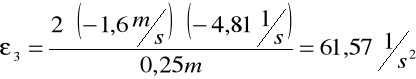
Obliczam przyspieszenie punktu D:

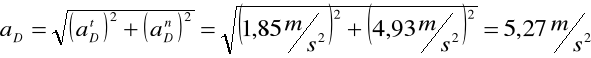
Obliczam przyspieszenie punktu S3:

• Wykresy z programu SAM:

wykres1:

φ₃=f(t)

odczytujemy dla t=0: φ₃=37⁰

wykres 2:

ω₃=f(t)

odczytujemy dla t=0: ω₃=4,81 1/s

wykres 3:

v_B=f(t), v_S3=f(t), v_D=f(t)

odczytujemy dla t=0: v_B=2000mm/s =2m/s, v_S3=816 mm/s =0,816 m/s,

v_D=384 mm/s =0384 m/s

wykres 4:

ε₃=f(t)

odczytujemy dla t=0: ε₃=61,44 1/s²

wykres 5:

a_B=f(t), a_S3=f(t), a_D=f(t)

odczytujemy dla t=0: a_B=0mm/s² =0m/s², a_S3=11115 mm/s² =11,115 m/s²,

a_D=5250 mm/s² =5,250 m/s²

• Porównanie wyników analizy kinematycznej dla zadanego położenia:

l.p.	Parametr	SAM	Metoda grafoanalityczna	Metoda analityczna
1.	φ3	37^0+180^0	217^0	36,87^0+180^0
2.	ω3	4,8 1/s	4,8 1/s	-4,81 1/s
3.	vB	2 m/s	2 m/s	-2 m/s
4.	vD	0,384 m/s	0,384 m/s	-0,384 m/s
5.	vS3	0,816 m/s	0,816 m/s	-0,817 m/s
6.	ε3	61,44 1/s^2	61,44 1/s^2	61,57 1/s^2
7.	aB	0	0	0
8.	aD	5,25 m/s^2	5,253 m/s^2	5,27 m/s^2
9.	aS3	11,115 m/s^2	11,114 m/s^2	11,18 m/s^2

Porównanie wyników wskazuje na zgodność obliczeń, co oznacza iż nie popełniono błędów w obliczeniach. Znak „minus” oznacza iż kierunek prędkości bądź przyspieszenia jest przeciwny do założonego układu współrzędnych, natomiast w metodzie grafoanalityczej podane są jedynie odczytane wartości, natomiast kierunki zaznaczone są na planie prędkości bądź przyspieszenia.

3. Analiza kinetostatyczna mechanizmu:

Do obliczeń kinetostatycznych przyjmujemy następujące dane:

J_S3=50*10^-3kgm²

m₃=4kg

g=9,81 m/s²

P₃=52N

M₃=5Nm

Obliczam :










3.1Mechanizm z układem sił zewnętrznych (bez P_R1):


3.2.Analiza sił działających na grupę strukturalną (2,3),(w celu wyznaczenia sił działających na mechanizm uwalniam grupę strukturalną od więzów):




W Autocadzie odczytuję wartości:

h1=93,5mm=0,094m

h2=110mm=0,11m

Zapisuję równania sił działających na poszczególne człony:










Zapisuję równanie sił działających na grupę strukturalną:




W celu znalezienia wartości
zapisuję równanie momentów względem punktu B:





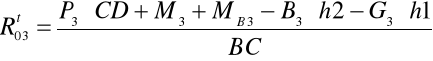
Podstawiam dane:




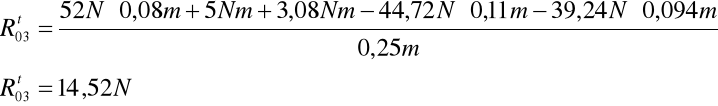
Na podstawie równania sił działających na grupę tworzymy plan sił:




Z planu sił odczytujemy:




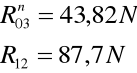
3.3Analiza sił działających na człon napędzający:

W Autocadzie odczytuję wartości:

h3=125,63mm=0,126m




Obliczam moment M_o:




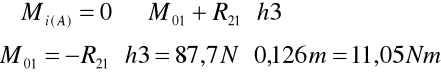
Zapisuję równania sił działających na człon napędowy:




Na podstwaie tego równania tworzę plan sił:




Z planu sił odczytuję:

R₀₁=70,03N

P_R1=53,4N

Wartośćsiły równoważącej, która była do wyznaczenia wynosi: P_R1=53,4N

3.4 Metoda mocy chwilowych:




Równanie mocy chwilowych ma postać:




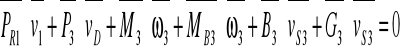
Po rozpisaniu iloczynów skalarnych otrzymujemy:




gdzie:


- kąt pomiędzy siłą B₃,a kierunkiem prędkości v_S3


- kąt pomiędzy siłą G₃,a kierunkiem prędkości v_S3




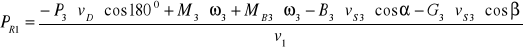
Podstawiam dane:




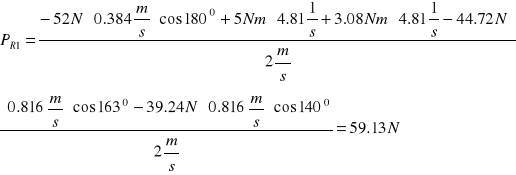
P_R1=59,13N

3.5 Analiza w programie SAM:

Model mechanizmu do analizy kinetostatycznej:




Wykres siły równoważącej P_R1:




Z wykresu odczytałem P_R1=-53,158N, znak „minus” wynika z tego, że siła ta działa przeciwnie do przyjętego kierunku dodatniego osi x.

3.6 Porównanie wyników analizy kinetostatycznej.

Metoda grafoanalityczna	Metoda mocy chwilowych	Program SAM
53,4N	59,13N	53,158 N

Porównanie wyników pokazuje, że obliczenia zostały wykonane poprawnie.

4

---