KIERUNEK Mechatronika

Realizowany w ramach projektu „Politechnika XXI wieku” współfinansowanego ze środków Unii Europejskiej
w ramach Europejskiego Funduszu Społecznego

ĆWICZENIE NR 3

Podstawy pomiarów wielkości geometrycznych technika współrzędnościową

Projekt Politechnika XXI wieku współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego;

Nr umowy UDA-POKL.04.01.01-00-121/09

Podstawy pomiarów wielkości geometrycznych technika współrzędnościową

Technika współrzędnościowa polega na wyznaczeniu elementów skojarzonych na podstawie współrzędnych zmierzonych punktów leżących na powierzchni przedmiotu. Matematycznie element skojarzony jest standardowym elementem geometrycznym (prosta, okrąg, płaszczyzna, walec) najlepiej dopasowanym do wartości pomiarowych. Element skojarzony jest podstawą do wyznaczenia cech geometrycznych przedmiotu (wymiary, odchyłki kształtu i położenia). W programach obliczeniowych stosuje się następujące metody najlepszego dopasowania:

• wg Gaussa (metoda najmniejszych kwadratów),

• wg Czebyszewa (kryterium minimum),

• obliczenie elementu wpisanego i opisanego,

• obliczenie elementu stycznego (zewnętrznego/wewnętrznego).

Metoda Gaussa polega obliczeniu elementu średniego. Podczas obliczeń wykorzystywana jest zasada, by suma kwadratów odległości punktów rzeczywistych od obliczonego elementu była najmniejsza.

Do pomiarów techniką współrzędnościową wykorzystywane są współrzędnościowe maszyny pomiarowe stanowiące skomplikowany układ pomiarowy, w skład którego wchodzą konstrukcja nośna, system lokalizacji punktów, systemy pomiarowe, system sterowania, komputer z oprogramowaniem sterująco- pomiarowym. Pomiary techniką współrzędnościową w przestrzeni 2D można wykonywać mikroskopem pomiarowym umożliwiającym pomiar współrzędnych punktu przedmiotu.

Rys. 1. Schemat pomiaru wałka techniką współrzędnościową; 1- tworząca rzeczywista, 2- tworząca wyznaczona (prosta skojarzona)

Przebieg ćwiczenia

• Zapoznać się z instrukcją obsługi i działaniem mikroskopu uniwersalnego

• Wałek umieścić w kłach mikroskopu uniwersalnego i ustawić tak, aby jego oś była w przybliżeniu równoległa do os X przesuwu wzdłużnego stolika pomiarowego. Ustawić ostrość widzenia krzyża głowicy goniometrycznej obracając nakrętką okularu. Następnie znaleźć krawędź wałka przemieszczając stolik pomiarowy przesuwem poprzecznym oś Y. Zwolnić blokadę tubusu i ustawić ostrość widzenia krawędzi zmieniając położenie tubusu. Zablokować tubus.

• Przyjąć jedną krawędź jako prostą odniesienia. Zmierzyć współrzędne dziesięciu punktów P_i rozłożonych równomiernie na całej krawędzi. Współrzędną X_i odczytujemy z okularu przesuwu wzdłużnego ze spiralą Archimedesa. Współrzędną Y_i odczytujemy z okularu przesuwu poprzecznego ze spiralą Archimedesa.

• Przesunąć stolik pomiarowy tak, aby krzyż głowicy goniometrycznej znalazł się na przeciwległej krawędzi (tworzącej walca). Odczytać współrzędne punktu P_k.

• Pomiary wykonać dla trzech przekrojów osiowych.

• Wyznaczyć niepewność pomiaru współrzędnych dla 10 powtórzeń. W tym celu dla ustalonego na krawędzi przedmiotu punktu P( x, y) nie zmieniając współrzędnej x zmierzyć współrzędną y odsuwając krzyż głowicy i ponownie dosuwając do krawędzi przedmiotu, a następnie nie zmieniając współrzędnej y zmierzyć współrzędną x tak jak poprzednio.

• Opracować procedurę obliczeniową równania prostej y=mx+b metodą najmniejszych kwadratów z wykorzystaniem arkusza kalkulacyjnego Microsoft Excel wg zależności:

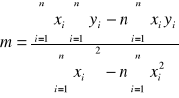
(1)

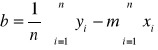
(2)

• Obliczenia wykonać dla wszystkich przekrojów.

• Wyznaczyć średnicę wałka wg zależności:

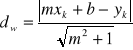
(3)

• Obliczenia wykonać dla wszystkich przekrojów.

• Wyznaczyć niepewność pomiaru współrzędnych x wykorzystując test T- Studenta, według następującej procedury

(4)

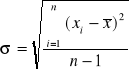
(5)

(6)

(7)

  poziom istotności. Przyjąć  0,05;

r= n-1 - liczba stopni swobody

t_;r - wartość statystyki t-Studenta odczytana z tablic

• Wyznaczyć niepewność pomiaru współrzędnych y wykorzystując test T- Studenta, według opisanej wyżej procedury .

• Sporządzić wykresy y=f(x) na podstawie danych pomiarowych i nanieść prostą wyznaczoną z zależności (1) i (2).

• Wyznaczyć błąd prostoliniowości tworzącej jako sumę największych odległości od prostej skojarzonej dwóch punktów leżących po jej przeciwnych stronach.

Literatura podstawowa

1. Kujan K.; Techniki i systemy pomiarowe w budowie maszyn: laboratorium. Wyd. Politechniki Lubelskiej, Lublin 2004

Literatura uzupełniająca

2. Instrukcja obsługi mikroskopu uniwersalnego

3. Malinowski J.; Jakubiec W. Metrologia wielkości geometrycznych. WNT W-wa 2004

1

---