Rozdział 4.

RUCH POCIĄGU

4.1. Model ruchu pociągu [13].

Pod pojęciem modelu ruchu pociągu będziemy rozumieć matematyczny opis ruchu uwzględniający trakcyjne siły (napędowe i hamujące) związane z podstawowym, ogólnie nieustalonym, ruchem pociągu w torze z uwzględnieniem zasadniczych i dodatkowych oporów przeciwdziałających temu ruchowi.

4.2. Podstawowe założenia.

Przy analizie podstawowego ruchu pociągu nie uwzględnia się zaburzeń ruchu (drgań) poszczególnych pojazdów. Przyjmuje się więc, że wszystkie pojazdy, tworzące pociąg, mają jednakowe prędkości wzdłuż toru. Zakładamy też równomierność rozkładu masy wzdłuż pociągu. Masę pociągu modelowo traktujemy jako skupioną w punkcie środka masy rzeczywistej. Siły działające na pociąg rozważamy jako wypadkowe poszczególnych oddziaływań, przyłożone do środka masy pociągu.

Zgodnie z uwagami zawartymi w p. 2.10, wyżej opisana idealizacja modelowa pociągu wymaga uwzględnienie przypadku ogólnego (najczęstszego w praktyce eksploatacyjnej), gdy pociąg, na jego całkowitej długości, znajduje się w torze charakteryzującym się różnymi nachyleniami (wzniesieniami i spadkami). Podczas ruchu pociągu w torze nachylenia pod pociągiem zmieniają się w funkcji czasu. W takim przypadku geodezyjny zapis profilu trasy nie może zostać wprowadzony do modelu pociągu wprost.

4.3. Przekształcenie profilu trasy do badania ruchu pociągu na modelu matematycznym [10],[13].

Opory dodatkowe ruchu składu pociągu długiego, znajdującego się na różnych profilach (wzniesieniach i spadkach) toru, są ogólnie zależne od długości L składu oraz od geodezyjnego profilu trasy pod składem w danym miejscu szlaku. Na szlaku kolejowym nie podaje się wysokości położenia miejsca szlaku nad poziomem odniesienia (morza). Podaje się jednak profil w postaci wartości wzniesienia lub spadku i(s) [%o], obowiązujący na danej długości toru Δs.

W punkcie S trasy elementarna siła dodatkowego oporu ruchu, pochodząca od wzniesienia i(s), wynosi dW_i. Oznaczając umowny nacisk jednostki długości pociągu na tor jako q [N/m], możemy napisać:

(4.1)

gdzie nacisk Q wyrażono w [N]; L - długość składu pociągu [m].

Zgodnie z rysunkiem 1 możemy więc napisać:

(4.2)

Rysunek 4.1. Opór wzniesienia elementarnej długości dl składu pociągu, znajdującego się w punkcie S na wzniesieniu i(s)[%o].

Rysunek 4.2. Skład pociągu na dowolnym geodezyjnym profilu toru

Przejdźmy do ilustracji pokazanej na rysunku 4.2. W chwili, gdy początek składu pociągu osiągnie punkt S_p, dodatkowy opór pociągu na wzniesieniu i(s), wyniesie:

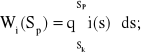
(4.3a)

Zgodnie bowiem z przyjętymi założeniami:

Możemy także napisać:

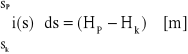
Zatem:
, albo:

(4.3.b)

Powyższy wzór (4.3.b) zachowuje moc, gdy pochylenie zastępcze i_zast jest wyrażone w radianach, zaś nacisk Q - w niutonach. Jeżeli jednak pochylenie zastępcze i_zast wyrazimy w promilach [%o], podobnie jak i(s), zaś nacisk Q w [kN], to opór dodatkowy pochodzący od wzniesienia i, w punkcie S_p, wyniesie:

(4.4)

Porównując stronami (4.3a) i (4.4), po odpowiednim uwzględnieniu (4.1) oraz wartości współczynników dla wyrażenia nacisku Q składu pociągu w kiloniutonach:

Q[kN] = 10^-3⋅q[N/m]⋅L[m], otrzymujemy:

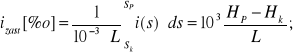
(4.5)

gdzie: i(s) jest wyrażone w [%o]; s - w [m]; L - w [m].

Jak widać, profil zastępczy toru wyraża się stosunkiem różnicy wysokości położenia czoła pociągu i końca pociągu do jego długości.

Wzór (4.5) nie jest wygodny do numerycznych obliczeń przekształconego profilu. Na mocy jego zapisu w postaci całkowej, dla bieżącego punktu S trasy, możemy napisać:

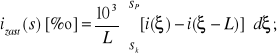
(4.6)

gdzie  - zmienna całkowania (droga).

W praktyce więc, znając zapis profilu trasy i(x), dla dowolnej długości pociągu L możemy ten profil przekształcić obliczeniowo traktując całkę (4.5) jako funkcję jej górnej granicy. Schemat analogowy przekształcenia profilu ciągłego, zgodnie z (4.6), przedstawiono na rysunku 4.3.

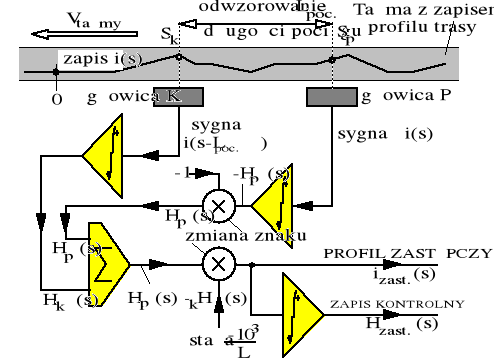
Rysunek 4.3. Schemat analogowy przekształcania geodezyjnie zdeterminowanego profilu trasy na profil zastępczy trasy odpowiadający długości pociągu L_poc.

Dla pojęciowego zilustrowania operacji numerycznych przekształcania profilu zdyskretyzowanego trasy szczególnie przejrzysta jest metoda wykreślna podana przez profesora Czeczotta. W metodzie tej przyrosty drogi Δs są skończone. Metoda ta polega na „zszywaniu” kolejnych wartości i_zast według ich wartości brzegowych na kolejnych przyrostach drogi Δs. Widzimy, że wierzchołki wzniesień i zagłębienia dolin ulegają „wygładzeniu”, co jest znaną właściwością procesu całkowania. Metoda Czeczotta odwzorowuje całkowanie z dużym krokiem. Po przekształceniu profilu trasy, pociąg można traktować jako punkt materialny na profilu zastępczym.

Geodezyjny zapis profilu trasy jest zawsze sporządzony w dziedzinie drogi. Historyczna metoda wykreślna (Czeczotta) pozwalała na wyznaczenie profilu zastępczego w dziedzinie drogi, niezależnie od czasu. Współcześnie, podczas symulacyjnego wyznaczania profilu zastępczego do wykonania są niezbędne operacje w dziedzinie czasu. Przyrosty drogi s i czasu t, należy przyporządkować odpowiednio.

Operacja analogowa według rys. 4.3, wymaga wzajemnego przyporządkowania prędkości przesuwu taśmy V_tasmy i rozstawu głowic a. Oznaczając gęstość zapisu profilu trasy na taśmie jako G_zap [m/cm] oraz rozstaw głowic jako a[cm], zwłoka czasowa t_Lpoc sygnału końca pociągu o długości L[m], w stosunku do początku pociągu wynosi:

Rysunek 4.4. Ilustracja metody Czeczotta wyznaczania zastępczego profilu toru przy zastosowaniu stałej wartości kroku s kolejnych przemieszczeń składu wzdłuż toru.

Rozstaw głowic a oblicza się z zależności:
zatem:

(4.7)

Metoda analogowa jest niezależna od prędkości pociągu V_poc.

Przy zastosowaniu całkowania cyfrowego, prowadzonego w dziedzinie czasu, należy przyporządkować odpowiednio kroki drogi Δs i czasu Δt do (dowolnej założonej) prędkości jazdy pociągu V_poc w przedziałach drogi:

Δs[m] = V_poc[m/s]⋅Δt[s];

4.3. Równanie ruchu pociągu

Wypadowa siła działająca na pociąg, traktowany jako punkt materialny o masie m, w jego ruchu niejednostajnym z prędkością V, wynosi F.

Zgodnie z II prawem Newtona:

F⋅dt = m⋅dV; (4.8a)

Ponieważ:
to możemy napisać:

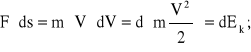
(4.8b)

gdzie E_k - energia kinetyczna pociągu.

Zgodnie z powyższym, elementarna praca siły czynnej F wzdłuż toru na przemieszczeniu elementarnym ds, jest równa elementarnemu przyrostowi energii kinetycznej E_k masy m w ruchu postępowym.

W pociągu, oprócz elementów poruszających się ruchem postępowym, występują elementy wirujące, których udział energetyczny jest znaczny. Całkowita energia kinetyczna pociągu E_poc wyraża się więc jako suma energii elementów poruszających się ruchem postępowym E_post, dodatkowo powiększona o sumę energii kinetycznej E_obr wszystkich elementów wirujących pojazdu: E_kpoc = E_kpost, + E_kobr, przy czym:

(4.9)

gdzie J_i - masowy moment bezwładności i - tego elementu wirującego z prędkością kątową _i.

Podczas trakcyjnego ruchu podstawowego (bez zaburzeń o charakterze wibracyjnym) stałe więzy kinematyczne w postaci przekładni zębatych, narzucone na prędkości obrotowe napędnych zestawów kół _jzest i wirników silników _jwirn zapewniają ścisłe przyporządkowanie tych prędkości.

(4.10)

gdzie i_k - przełożenie kinematyczne przekładni pomiędzy wirnikiem silnika a napędnym zestawem kół rozumiane jako stosunek liczby zębów wieńca koła zębatego obejmującego oś zestawu do liczby zębów zębnika napędzanego bezpośrednio od wału wirnika (najczęściej osadzonego wprost na tym wale).

Grupując odpowiednio elementy wirujące sprzężone z zestawami napędnymi „n” oraz nie-napędnymi (tocznymi - „t”), możemy równanie (4.8b) napisać w następującej postaci:

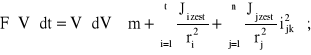
(4.11)

gdzie: r=d_k/2; i ∈ t; j ∈ n;

Otrzymujemy uproszczoną formę zapisu równania (4.8):

(4.12)

gdzie: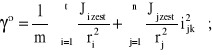

Wielkość γ° nazywamy współczynnikiem mas wirujących. Współczynnik ten opisuje ilościowy udział energii kinetycznej mas wirujących w całkowitej energii kinetycznej pociągu. Niekiedy w literaturze spotyka się potraktowanie łączne mas w ruchu postępowym i wirującym

γ = 1+γ°; (4.13)

Przybliżone wartości współczynnika mas wirujących podano w tabeli.

Tabela 4.1.

Rodzaj pojazdu szynowego	γ = 1+γ°
Wagony osobowe i towarowe: dwuosiowe załadowane, czteroosiowe próżne.	1,03 ÷ 1,10
Wagony silnikowe	1,1 ÷ 1,15
Lokomotywy elektryczne (4 i 6 osiowe)	1,2 ÷ 1,3

4.3.1. Pierwsza, ogólna postać równania ruchu pociągu

Wzór (4.8a), po uwzględnieniu (4.13), przedstawia pierwszą postać równania ruchu pociągu (RRP):

(4.14)

W powyższym równaniu obowiązują jednostki SI (Standard International):

m - [kg=Ns²/m]; γ - [1]; F - [N]; V - [m/s].

Pierwsza postać RRP stanowi podstawowy model matematyczny ruchu pociągu. W modelu tym masa m jest traktowana jako skupiona w jednym punkcie, na który działa wypadkowa siła czynna (zewnętrzna) F(V):

(4.15)

Siła oporu ruchu pociągu
, występująca niejawnie w zapisie (4.14), powinna być rozumiana zgodnie z rysunkiem 4.5a), jako wyznaczona na profilu zmodyfikowanym według (4.6).

4.3.2. Druga, technicznie stosowana postać równania ruchu pociągu

Dzieląc stronami równanie (4.15) przez nacisk Q pociągu na tor otrzymujemy zapis jednostkowej siły przyśpieszającej f_a według rysunku 4.5a).

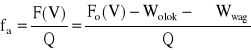
(4.16)

gdzie obowiązują następujące jednostki fizyczne: f_a - [N/kN]; Q - [kN]; F_o(V) - [N]; W(V) - [N].

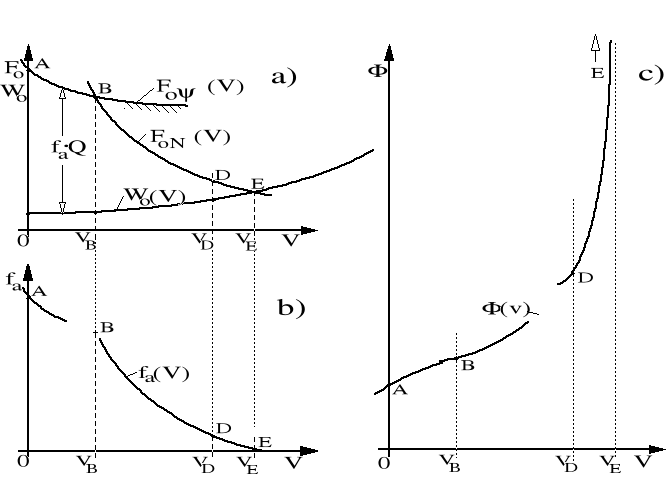
Rysunek 4.5. Ilustracja jednostkowej siły przyśpieszającej f_a oraz funkcji (V).

Jednostkowa siła przyśpieszająca wyraża stosunek wypadkowej podłużnej siły czynnej działającej na pociąg do siły Q grawitacyjnego nacisku pociągu na tor:

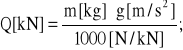
(4.17)

W wyniku podstawienia (4.16) i (4.17) do (4.14) otrzymujemy po uporządkowaniu drugą postać RRP, stosowaną w praktyce kolejnictwa.

(4.18)

Wielkości f_a(V) oraz F(V) zilustrowano rysunkiem 4.5.

W tym miejscu należy podkreślić, że w przypadku hamowania pociągu, w miejsce jednostkowej siły przyśpieszającej pojawia się jednostkowa siła hamująca f_h:

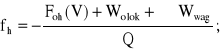
(4.19)

Równanie ruchu pociągu rozwiązuje się w celu wyznaczenia czasu i drogi rozruchu (hamowania) pociągu zarówno dla potrzeb projektowania hamulców pociągu jak i urządzeń infrastruktury (odległości między-sygnałowe). Ponadto, wyznaczenie rozkładu prędkości ruchu składu pociągu (w dziedzinie czasu i drogi) jest niezbędne konstruktorom pojazdów przy projektowaniu taboru, przy zmęczeniowych obliczeniach elementów konstrukcji.

4.3.3. Trzecia, historyczna postać równania ruchu pociągu

Trzecia postać RRP współcześnie ma znaczenie jedynie historyczne. Postać tę można spotkać w starej literaturze kolejowej z pierwszych dwóch dziesięcioleci XX wieku, kiedy RRP stosowano przede wszystkim w planowaniu ciężkich towarowych przewozów gospodarczych i militarnych. W owym czasie, podobnie jak i dziś, społeczeństwa posługiwały się popularnymi jednostkami miar prędkości V[km/h]. W historycznym rozwoju teorii ruchu pociągu dla celów technicznych, początkowo zastosowano podobne, wówczas społecznie akceptowane, jednostki miar przyśpieszenia [km/h²], według następującego przelicznika na jednostki stosowane współcześnie:

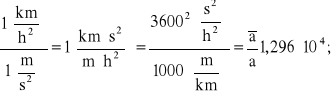
zatem:
;

Ponieważ w towarowym transporcie kolejowym średnia wartość współczynnika γ mas wirujących może być przyjęta jako γ_śr ≈ 1,06; to w przybliżeniu można równanie (4.18) napisać w następującej postaci:

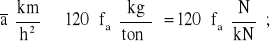
(4.20)

gdzie czas wyrażono w godzinach.

Trzecia postać RRP, niezależnie od archaicznych jednostek miar, jest mało dokładna, gdyż operuje średnią wartością współczynnika mas wirujących. Informacja o tej postaci równania ma znaczenie zarówno informacyjne, (techniczno - erudycyjne) jak i ostrzegawcze.

4.4 Rozwiązywanie równania ruchu pociągu

Podstawowa trudność w --> rozwi[Author:JM] ązywaniu elementarnego, zwyczajnego równania różniczkowego pierwszego rzędu (4.18), polega na uzależnieniu wartości jednostkowej siły przyśpieszającej (hamującej) równocześnie od dwóch zmiennych niezależnych: drogi s i czasu t według geodezyjnych warunków profilu trasy (drogi) pokonywanej w czasie; f_a/h =f(V, s, t). Wynikiem rozwiązania RRP (4.18) jest przebieg prędkości pociągu w funkcji drogi V(s) na szlaku rzeczywistym (geodezyjnym) oraz w funkcji czasu V(t). Operacja całkowania RRP według (4.18) jest formalnie bardzo prosta:

(4.21)

zatem w i-tym przedziale przyrostu prędkości ΔV_i: od początkowej V_ip do końcowej V_ik, niezbędny przyrost czasu t_i procesu (p - początek, k - koniec), wyznacza się na podstawie elementarnego całkowania:

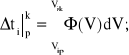
(4.22)

Podobnie, na mocy (4.21) wyznacza się przyrost drogi.

Podstawiając do (4.22): Δs = V⋅Δt oraz ds = V⋅dt = V⋅(V)⋅dV, otrzymujemy przyrost drogi (odpowiednio) w i-tym przedziale prędkości:

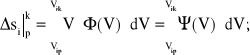
(4.23)

gdzie Ψ(V) = Φ(V)⋅V

Gęstość przedziałów prędkości powinna być dobrana stosownie do oczekiwanej dokładności obliczeń numerycznych.

Średnie przyśpieszenie w i-tym przedziale prędkości wynosi:

(4.24)

Dla wybrania odpowiedniej metody całkowania RRP należy zbadać postać funkcji Φ(V) oraz Ψ(V), występujących w wyrażeniach (4.22) i (4.23).

Ponieważ wielkość Φ(V) występuje w mianowniku (4.18) to nie powinna ona osiągać wartości zero. W praktyce tak się projektuje parametry procesu trakcyjnego (według rysunku 4.4) aby przy maksymalnej prędkości przewozowej V_D był pewien zapas jednostkowej siły przyspieszającej f_a⋅Q. Tylko wtedy całki (4.22) i (4.23) mają wartości skończone. Osiągnięcie prędkości V_E, przy której siła przyśpieszająca jest zerowa, wymagałoby nieskończenie wielkiego czasu. W praktyce kolejowej więc tak się dobiera moce lokomotyw i składy wagonów aby w topograficznie określonych warunkach wniesień i spadków toru, z oczekiwaną prędkością V_D, jednostkowa siła przyśpieszająca f_a przy dochodzeniu do tej prędkości nie była mniejsza niż 1[N/kN].

Rysunek 4.5c) wyjaśnia zagadnienie nieskończoności całki przy prędkości V_E.

Przykładowe parametry ruchu składu pociągów podano w tabeli 4.2.

Tabela 4.2.

RODZAJ POCIĄGU	V max [km/h]	Odl. [km] m. przyst.	Przyśp. rozruchu [m/s^2]
						Przy V≥ 0	Przy VD
Towarowy	60 ÷ 80	-----	0,15 ÷ 0,2	0,06 ÷ 0,01
Pasażerski pośpieszny	120 ÷ 160	40 ÷ 60	0,35 ÷ 0,5	0,03 ÷ 0,04
Pasażerski lokalny	70 ÷ 120	2 ÷ 8	0,3 ÷ 0,4	0,02 ÷ 0,03
Zespół trakcyjny dalekob.	100 →	20 ÷ 60	0,4 ÷ 0,6	0,03 ÷ 0,05
Zespół trakcyjny podm.	80 ÷ 120	1,3 ÷ 3	0,6 ÷ 0,8	0.05 ÷ 0,07
Pociąg Metro	60 ÷ 90	0,6 ÷ 1,0	0,8 ÷ 1,2	0,08 ÷ 0,15
Praca manewrowa	→ 20	-----	0,1 ÷ 0,15	0,005 ÷0,01

4.4.1. Całkowanie numeryczne równania ruchu pociągu

Wybór metody numerycznego całkowania RRP należy do wykonawcy obliczeń (autora programu). Pośród kilku metod przybliżonych całkowana RRP w tym miejscu omówiona zostanie metoda parabol, (metoda Simpsona), znacznie dokładniejsza od metod prostokątów i trapezów, szczególnie dogodna do zastosowań w dużych przedziałach, w których funkcja f_a(V) ma ciągłą pochodną. Jedynym ograniczeniem metody jest parzysta liczba pod-przedziałów wewnątrz tych dużych przedziałów ciągłości.

Zgodnie z pokazaną na rysunku 4.5 charakterystyką sił przyśpieszających, warunek ciągłości jest spełniony w dwóch dużych przedziałach:

0 < V_I ≤ V_B, oraz V_B < V_II ≤ V_D. W takich warunkach liczbę dużych przedziałów całkowania możemy ograniczyć do 2, przyjmując podział każdego z nich na parzystą liczbę odcinków, co najmniej 2.

Zgodnie z metodą Simpsona, (której zasady podane są w każdym poradniku matematyki wyższej), wystarczy znać wartości brzegowe oraz środkowe funkcji w poszczególnych przedziałach całkowania. Należy więc znać wartości jednostkowej siły przyśpieszającej f_a, co najmniej w pięciu punktach, odpowiadających następującym prędkościom, według oznaczeń przyjętych na rysunku 4.4:

[V = 0], [V_B/2]; [V_B]; [V_B + (V_D − V_B) /2]; [V_D];

W ten sposób przedziały AB i BD ciągłości funkcji (V), według rysunku 4.4c), zostały podzielone na 2 jednakowe części każdy.

Ogólne wzory całkowania według metody Simpsona zostały podane poniżej.

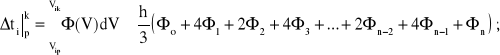
przy czym
(4.25)

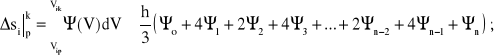
przy czym
(4.26)

Obliczając kolejno Δt_AB, Δt_BD, Δs_AB, i Δs_BD, zgodnie z rysunkiem 4.5, wyznaczamy całkowity czas rozruchu pociągu od prędkości V_o= 0 do prędkości V_D.

(4.27)

oraz całkowitą drogę rozruchu pociągu.

(4.28)

Dla liczby pod-przedziałów n = 2, powyższe wzory upraszczają się znacznie.

Obliczenia takie prowadzi się na odcinkach o stałej wartości zastępczego profilu toru i_zast[%o] = const. W przypadku zmiany pochylenia szlaku (wzniesienia lub spadku) w punkcie S_x trasy należy obliczenia przerwać i po wyznaczeniu nowych, odpowiednich wartości współczynników, kontynuować je aż do osiągnięcia prędkości V_D.

4.5. Podstawowe parametry ruchowe pociągu

Charakterystyczne prędkości pociągu [13].

Podstawową prędkością charakterystyczną pociągu jest prędkość przewozowa albo podróżna V_P. Jest ona wyrażona stosunkiem długości trasy do całkowitego czasu przejazdu tej trasy (wliczając czasy postojów). Prędkość przewozowa stanowi przedmiot zainteresowania przewoźników i klientów od strony eksploatacyjno - organizacyjnej. Prędkość przewozową wyznacza się na etapie planowania rozkładu jazdy.

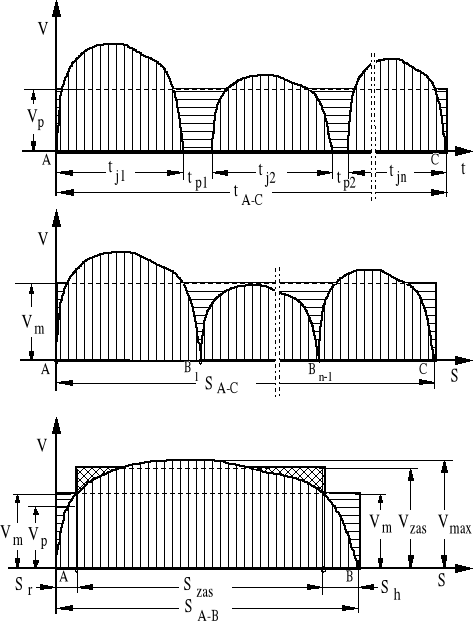
Rysunek 4.6. Rozkłady prędkości pociągu: u góry - w dziedzinie czasu; pośrodku - w dziedzinie drogi; u dołu - porównanie rodzajów prędkości w funkcji drogi na pojedynczym odcinku trasy.

Zgodnie z rysunkiem 4.6 łączny czas niezbędny do przemieszczenia pociągu z punktu A trasy do punktu C wyrazi się jako suma czasów jazdy t_j na poszczególnych odcinkach międzyprzystankowych oraz czasów postojów t_p na przystankach.

(4.29)

Kategorie ruchu: j - jazda; p - postój.

n - liczba odcinków międzyprzystankowych,

n-1 - liczba przystanków.

Wzór (4.29) możemy zapisać krócej:

(4.30)

gdzie:
przy czym:

t_ji - czas przejazdu i - tego odcinka,

t_pk - czas postoju na k - tym przystanku,

t _A-C - czas całkowity na odcinku A-C.

Prędkość podróżna, zgodnie z rysunkiem 4.6, wyrazi się następująco:

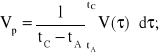
(4.31)

albo inaczej:

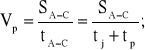
(4.32)

Prędkość przewozowa wynika w naturalny sposób z rejestracji przebiegu prędkości jazdy w funkcji czasu. Jest to wartość średnia całkowa prędkości zarejestrowanej w funkcji czasu t przemieszczania składu pociągu wzdłuż szlaku. Odpowiednią ilustrację pokazano w górnej części rysunku 4.6.

Inną, stosowaną w zagadnieniach technicznych charakterystyczną prędkością pociągu jest tzw. prędkość średnia jazdy. Prędkość ta stanowi bardzo ważny czynnik w prognozowaniu zużycia energii i elementów pojazdu (hamulce) a także w doborze mocy pojazdu trakcyjnego do zadań przewozowych.

Średnia prędkość jazdy wynika w naturalny sposób z rejestracji przebiegu prędkości jazdy w funkcji przebytej przez pociąg drogi. Jest to wartość średnia całkowa prędkości zarejestrowanej w funkcji drogi s. Odpowiednią ilustrację pokazano w środkowej części rysunku 4.6.

Zgodnie z rysunkiem 4.6, prędkość średnia jazdy może być zapisana jako stosunek długości drogi S_A-C do czasu jazdy t_j (bez uwzględniania czasu postojów na przystankach):

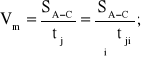
(33)

Po uwzględnieniu (4.32), możemy napisać: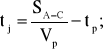

Zatem, według (4.33), otrzymujemy:

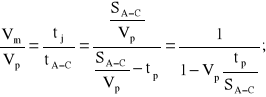
(4.34)

Wartość t_p/S_A-C wyraża jednostkowe zużycie czasu na postój, przypadająca na 1 kilometr trasy, [wyrażone w sekundach na kilometr; s/km].

Przybliżone wartości średnich jednostkowych (względnych) czasów postoju zależą od rodzaju pociągu i przybierają następujące wartości:

Tabela 4.3.

RODZAJ POCIĄGU	tP/SA-C [s/km]
Pośpieszny	3
Lokalny	9±3
Podmiejski	15±3

Przy projektowaniu taboru należy uwzględniać wyższe prędkości niż V_m, charakteryzujące się największą gęstością prawdopodobieństwa wystąpienia na trasie. Dla potrzeb projektowania wprowadzono pojęcie prędkości zasadniczej V_zas, która została zilustrowana rysunkiem 4.6, w jego dolnej części. Prędkość zasadnicza stanowi średnią wartość całkową ruchu z prędkościami powyżej V_m, czyli po odrzuceniu procesu rozruchu i hamownia pociągu. Prędkość zasadniczą możemy utożsamiać z „prędkością konstrukcyjną”.

(4.35)

Oprócz prędkości zasadniczej ważne znaczenie ma prędkość maksymalna stanowiąca ograniczenie od strony bezpieczeństwa ruchu zestawów w torze, mechanicznej wytrzymałości wirników silników i niezawodności łożysk.

V_max>V_zas>V_m>V_p;

4.6. Wyznaczanie mocy znamionowej pojazdu trakcyjnego [10],[13].

Przy oszczędnej gospodarce taborowej moc pojazdu trakcyjnego nie powinna zbytnio przewyższać wartości wynikającej z potrzeb przewozowych.

Moc pojazdu trakcyjnego stanowi zakres zainteresowania zarówno konstruktorów taboru ja i jego użytkowników:

♦Konstruktor, stosownie do wartości mocy pojazdu, prowadzi obliczenia trakcyjne, energetyczne, wytrzymałościowe, niezawodnościowe i funkcjonalne.

♦Przewoźnik (kolej) oblicza moc pojazdu przy dokonywaniu zakupu taboru przeznaczonego do realizacji jego polityki przewozowej na określonej trasie z uwzględnieniem gotowości technicznej, oszczędności energetycznej, unifikacji, podatności utrzymaniowej i naprawczej, ergonomii, ekonomii i autoreklamy.

Punktem wyjścia do wyznaczenia niezbędnej wartości mocy silników pojazdu trakcyjnego są takie wielkości jak: - masa i rodzaj ładunków, - strumień towaru w czasie, - rodzaj pociągu, - liczba wagonów w pojedynczym składzie, - wymagania ruchu międzynarodowego, - prędkość zasadnicza i profil trasy. Z pojęciem prędkości zasadniczej są sprzężone takie zagadnienia jak: - odległości międzyprzystankowe, - wartości przyśpieszeń rozruchu i hamowania, - wskaźniki energetyczne.

Rysunek 4.7. Charakterystyka ogólna pojazdu trakcyjnego.

W przedziale B-D charakterystyki moc znamionowa pojazdu, odniesiona do osi zestawów napędnych, jest opisana związkiem:

(4.36)

gdzie siła F_oD jest wyrażona w [kN], zaś prędkość V -[m/s];

Nadwyżka siły przyśpieszającej końca rozruchu F_oD wyrazi się następująco:

(4.37)

przy czym: f_a - [N/kN]; Q - [kN];

Na torze prostym i poziomym, obowiązuje następujący bilans sił:

albo:

(4.38)

gdzie: W_zas - opór zasadniczy pociągu,

Q - łączny nacisk pociągu na tor,

a - przyśpieszenie rozruchu [m/s²];

Ponieważ Q = m⋅g, to F_o = γ⋅a⋅M + W_zas [kN]

gdzie: M - masa całkowita składu pociągu (brutto) [t];

Na wzniesieniu uogólnionym opór pociągu rośnie:

gdzie: i - [%o]; Q - [kN]; W - [kN];

Wzniesieniem uogólnionym nazywamy tu albo rzeczywiste wzniesienie zastępcze albo wzniesienie przeliczeniowe odwzorowujące siły pochodzące od krzywizn toru.

Zatem na wzniesieniu siła Fo wyniesie:

F_o = γ⋅a⋅M + W_zas + W_i; [kN]

Zgodnie z (4.36) możemy więc łączną moc silników trakcyjnych lokomotywy wyrazić jako:

(4.39)

gdzie: a - [m/s²] przyśpieszenie końca rozruchu (w punkcie D charakterystyki),

η_p - sprawność przekładni pomiędzy silnikiem a zestawami napędnymi.

W_zas - [kN]; W_i - [kN]; V_D - [m/s];

W przypadku lokomotyw spalinowych należy uwzględnić niezbędną rezerwę mocy ok. 5% ze względu na nie przeciążalny silnik.

4.7. Wyznaczanie minimalnego nacisku napędnych zestawów kół pojazdu trakcyjnego na tor [10],[13].

Znając wartości mocy znamionowej pojazdu trakcyjnego, zgodnie z rysunkiem 4.7, dla określonego składu pociągu możemy wyznaczyć największe wzniesienie, które pojazd trakcyjny pokona przy wywiązywaniu siły pociągowej określonej w punkcie B charakterystyki. W praktyce spotykamy najczęściej zadanie odwrotne: znając zastępczy profil toru i[%o] oraz parametry składu pociągu (masa brutto, długość, prędkość) i dobieramy odpowiednią lokomotywę do realizacji zadania przewozowego.

W punkcie B siła przyczepności F_o równa jest sile F_oN wywiązywanej na osiach lokomotywy przez jej zespoły napędowe. W tym punkcie charakterystyki, wartość mocy N_o jest znana, wynikająca ze związku (4.39). Możemy więc napisać, zgodnie z (4.39):

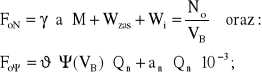
(4.40)

gdzie: Q_n - łączny nacisk zestawów napędnych na tor [kN];

a_n - współczynnik oporu ruchu zestawów napędnych [N/kN];

ϑ - współczynnik wykorzystania nacisku napędnego (bezwymiarowy)

Ψ- współczynnik przyczepności kół do szyn (bezwymiarowy).

M - [t]; W_z - [kN]; W_i - [kN]; N_o - [kW]; V_B - [m/s];

Dla przypadku F_oN = F_o, minimalny nacisk napędny Q_n wyznaczamy na mocy (4.40):

(4.41)

a_B = a(V_B); _B = (V_B); W_zasB = W_zas (V_B);

Wyznaczając Q_n należy uwzględniać niekorzystne warunki atmosferyczne (szyny wilgotne).

Liczba z_n zestawów napędnych w lokomotywie jest określona przez stosunek wartości łącznego nacisku napędnego lokomotywy Q_n do wartości dopuszczalnego nacisku pojedynczego zestawu na tor Q_dop.

(4.42)

Wartość Q_dop jest określona według kategorii linii kolejowej.

Liczba zestawów napędnych określa racjonalną postać konstrukcyjną lokomotyw spalinowych. Należy napędzać tylko niezbędną liczbę osi. Lokomotywy spalinowe charakteryzują się szczególnie niekorzystnym wskaźnikiem mocy do masy [kW/t] gdyż zawierają liczne przetworniki energii pracujące w strukturze szeregowej: Silnik spalinowy - generator główny - silniki trakcyjne.

4.8. Wykorzystanie równania ruchu pociągu (RRP) w zadaniach projektowych taboru trakcyjnego [10].

W wyniku rozwiązania RRP otrzymujemy funkcję V(s) lub V(t) dla określonego składu pociągu na określonym odcinku drogi s lub w czasie t na określonym odcinku szlaku kolejowego. Punktem wyjścia do rozwiązania RRP jest charakterystyka pojazdu trakcyjnego prowadzącego pociąg, znajomość zasadniczych oporów ruchu składu pociągu oraz znajomość terenowej topografii toru kolejowego.

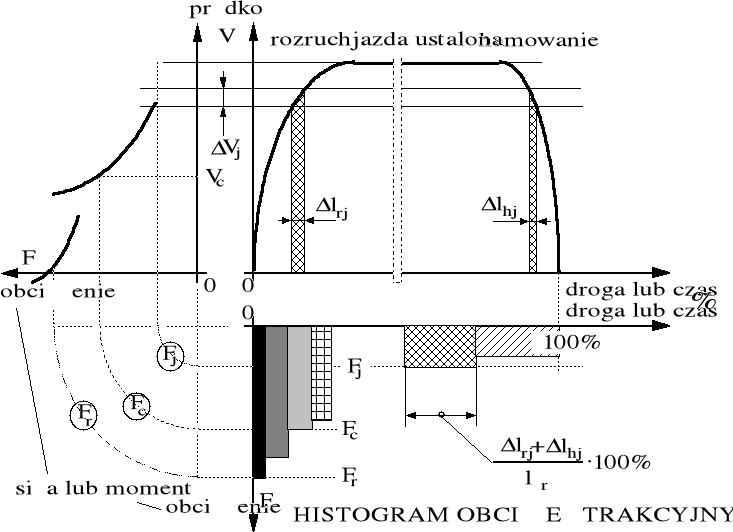
Rysunek 4.8. Budowa histogramu obciążeń trakcyjnych na użytek konstruktora podwozia i napędu pojazdu trakcyjnego.

Charakterystyka trakcyjna określa wartości sił w funkcji zmiennej w czasie prędkości a tym samym określa wartości mocy pojazdu trakcyjnego w czasie. Zależnie od struktury programu obliczeniowego możemy uzyskać informacje niezbędne dla konstruktora pojazdu (siły w węzłach konstrukcyjnych) lub dla konstruktora przetworników energii (moce). Rozkłady tych wielkości (sił i mocy) w czasie, najczęściej w ujęciu procentowym, wykorzystuje się w zmęczeniowych obliczeniach przekładni zębatych, łożysk tocznych, układów smarowania, układów chłodzenia itp. Rozkłady takie są nazywane histogramami. Na rysunku 4.8 pokazano zasadę budowy histogramu obciążeń odniesionych do osi napędnych zestawów kół pojazdu trakcyjnego. Rysunek 4.9 ilustruje odmiany ujęć redakcyjnych histogramów.

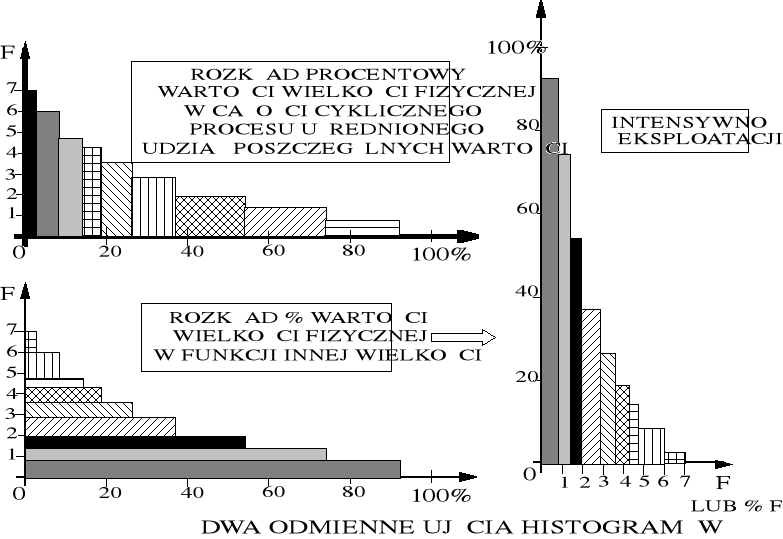
Rysunek 4.9. Przykładowe odmiany redakcyjnego ujęcia histogramów.

4.9. Wykorzystanie równania ruchu pociągu (RRP) w planowaniu przewozów energooszczędnych [10].

Zużycie energii na określonej trasie w znacznym stopniu zależy od prędkości podróżnej i sposobu prowadzenia pociągu. Dwa nieposkromione dążenia ludzkie: - wzrost prędkości przewozów i: - zmniejszenie jednostkowych rozchodów energii, są względem siebie ogólnie sprzeczne. Wobec powyższego szeroko stosuje się „przejazdy” symulacyjne dla dokonania wyboru możliwie energooszczędnego sposobu prowadzenia pociągu z zadaną prędkością przewozową na określonej trasie.

Zbudowana w ten sposób instrukcja dla maszynisty może mieć charakter zdeterminowany z przyporządkowaniem zaleceń jazdy nastawnika na określonej pozycji nastawnika po określonym odcinku trasy. Innym sposobem wspomagania decyzji maszynisty jest wyposażenie pojazdu w odpowiednio oprogramowany komputer pokładowy analizujący sytuację na bieżąco, stosownie do zaistniałych czynników losowych. Jeszcze dalej posunięte zastosowanie technik symulacyjnych pozwala na całkowite wyeliminowanie decyzji maszynisty odnośnie prowadzenia pociągu. W takim przypadku maszynista pełni rolę dyżurnego reagującego jedynie na nadzwyczajne zdarzenia mogące zagrażać bezpieczeństwu ruchu. Najdalsze wykorzystanie symulacyjnego planowania przewozów przy wykorzystaniu RRP zachodzi przy całkowitej eliminacji maszynisty, na przykład w taborze metro, który - w takim przypadku - pracuje jako „pozioma winda”, zatrzymująca się na wszystkich zaplanowanych przystankach.

4.10. Praca jednostkowa członów napędowych pociągu [13].

Przemieszczenie masy M (brutto) pociągu na odległość S wymaga pokonania oporów ruchu, zależnych od rodzaju pociągu, prędkości, profilu trasy... itp., na pokonywanej przez pociąg trasie.

Praca L wykonana przez pojazd trakcyjny w czasie T przejazdu pociągu na trasie S [km], może być wyrażona następująco:

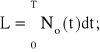
(4.43)

gdzie: N_o - moc pojazdu trakcyjnego [W],

T - czas przejazdu trasy S [s];

Jeżeli wielkość L podzielimy przez iloczyn masy brutto M i drogi S, to otrzymamy wskaźnik  [N⋅m/t⋅km], będący porównawczym (ilościowym) wyróżnikiem energetycznej sprawności przemieszczania składu pociągu (a w tym i ładunku).

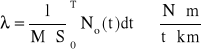
(4.44)

Wartość wyróżnika λ pozwala porównawczo wnioskować o techniczno - energetycznej jakości różnych lokomotyw co ma poważne gospodarcze znaczenie dla przewoźnika.

W praktyce pomiary prowadzi się w sposób zdyskretyzowany, w krótkich odcinkach czasu t_x:

(4.45)

Ponieważ w krótkim, elementarnym odcinku czasu t_x moc N_x wyraża się jako iloczyn prędkości i chwilowych, łącznych oporów ruchu pociągu W_ox (wraz z oporem akceleracji), to możemy napisać:

(4.46)

albo:

gdzie n - liczba elementarnych odcinków trasy S przejeżdżanych „z mocą”.

Należy tu rozumieć zarówno moc napędzającą jak i moc hamującą odzyskowo; t_x - czas jazdy na odcinku „x” trasy, V_x - średnia prędkość jazdy na odcinku „x”.

Wskaźnik pracy jednostkowej możemy więc wyznaczyć na podsatwie następującego wzoru:

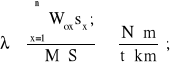
(4.47)

Dla określonej, średniej prości jazdy V_m na oscinku S trasy możemy, posługując się wzorem (4.47), wyznaczyć średni opór ruchu W_m przy podstawieniu:
skąd otrzymujemy:

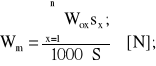
(4.48)

gdzie:
S - [km]; W_x - [N].

1

71

i(s) [%o]

droga s

dl

V

q⋅dl

dW_i

S

Siła

Prędkość

l₁

l₂

l₃

L

droga s

H_k1

s

s

s

i_zast.1

i_zast.2

H_p1

P₁

P₂

F_N(V) = N/V

Q - nacisk [N]

ψ - współczynnik przyczepności [1]

F - siła [N]

N - moc [W]

V [m/s]

F [N]

V_max=V_D

Wzniesienie I

Tor poziomy

OPORY RUCHU

W(V)

Siła przyśpieszająca

Wzniesienie II

F_a* = F_a (V*) = F_N (V*) - W(V*)

V*

F_a*

F_ψ(V) = Q⋅ψ(V)

A

D

B

P

K

droga s

H_p

S_p

H_k

L

S_k

---