Rozdział 2.

OPORY RUCHU POCIĄGU. ISTOTA ZJAWISKA I BADANIA.

Pod pojęciem oporów ruchu pociągu należy rozumieć siły przeciwdziałające ruchowi składu w torze, bez względu na ich fizyczne pochodzenie. Podział oporów ruchu przedstawiono na diagramie 2.1.

Siły przeciwdziałające ruchowi składu pociągu w torze wyidealizowanym, doskonale prostym i poziomym, nazywamy oporami zasadniczymi. Są to „opory własne” składu pociągu. Zgodnie z diagramem 2.1, opory zasadnicze uwzględniają także opory aerodynamiczne w wolnej pół-przestrzeni nieruchomego powietrza nad powierzchnią toru oraz opór wiatru. Opory wywołane wpływem krzywizn, wzniesień, spadków, ruchu w tunelu, traktujemy jako dodatkowe (geodezyjne i infrastrukturalne).

Pośród oporów „własnych” występują siły dyssypacji, związane z rozpraszaniem energii drgań w tłumikach hydraulicznych umieszczonych w podwoziu pojazdu poruszającego się po nierównościach toru. Pośród oporów „dodatkowych” także występują siły dyssypacji związane z rozpraszaniem energii drgań w podtorzu, wywołanych ruchem pojazdu. Istnieje ścisłe sprzężenie przyczynowo - skutkowe tych dwóch zjawisk tak, że ich badawcze oddzielenie jest trudne. Ogólnie należy mówić o dyssypacji energii w systemie pojazd - tor. W tabeli sprzężenie to zostało zaznaczone linią przerywaną.

Opór toczenia się kół po szynach omówiono w punkcie

Opór spinu omówiono w punkcie 1.5.

Jako trzecią składową mechanicznego oporu ruchu można wymienić uśrednioną siłę traconą udarowo, zwłaszcza na torach stykowych i w rozjazdach.

(2.1)

Wypadkowy opór ruchu koła po szynie wyraża się w postaci sumy trzech składowych:

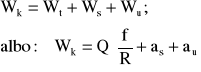
(2.2)

2.1. Opór ruchu pochodzący od łożysk kół [1] [13].

Tradycyjnie moment oporu ruchu w łożysku opisuje się następującym wzorem:

(2.3)

gdzie: Q_L - promieniowe obciążenie łożyska,  - współczynnik tarcia pomiędzy czopem i panewką, d_cz - średnica czopa.

Opr_tab

Diagram 2.1. Podział oporów ruchu pociągu (dotyczy wszystkich pojazdów trakcji adhezyjnej).

Wzór (2.3) stosuje się także do łożysk tocznych, które - podobnie jak koło po szynie - podlegają zjawisku oporu toczenia a ponadto występuje przepychanie smaru i tarcie uszczelnień. Wartości współczynnika  zawierają się w granicach 0,001 <  < 0,0015.

Pochodząca od pracy łożysk składowa oporu ruchu składu pociągu W_Ł wyraża się następującym wzorem:

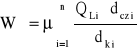
(2.4)

gdzie: Q_Li - promieniowe obciążenie i-tego łożyska,

d_{cz i} - średnica czopa i-tej osi zestawu,

d_{k i} - średnica okręgu tocznego kół i- tego zestawu,

n - liczba zestawów w składzie pociągu.

2.2. Opór ruchu koła łożyskowanego [13].

W praktyce badawczej współczesnego taboru wzory (2.2) i (2.4) przedstawia się łącznie, w prostej postaci uwzględniającej łączny opór toczenia się koła po szynie, opór w łożyskach tocznych, opór spinu i opór udarów torowych, oddzielnie dla zestawów napędnych i oddzielnie dla zestawów tocznych:

(2.5)

Współczynniki a_t i a_n wynoszą odpowiednio: a_t = 1,5 ÷ 2 [N/kN];

a_n = 2 ÷ 3 [N/kN];

2.3. Opór aerodynamiczny [2].

W praktyce kolejowej posługujemy się wzorami empirycznymi ujmującymi w sposób przybliżony złożony stan oddziaływań aerodynamicznych w każdym pojeździe pociągu. Stwierdzono więc, że - wypadkowo ujęty - opór powietrza jest zależny od: kwadratu prędkości ruchu, skrajni taboru, kształtu powierzchni czołowej lokomotywy, kształtu pojazdu końcowego i gęstości powietrza.

We wzorach doświadczalnych, opisujących opór aerodynamiczny W_A na podstawie badań, występują następujące parametry:

• prędkość jazdy V [m/s];

• gęstość powietrza ρ [kg/m³];

• powierzchnia poprzecznego przekroju pociągu (skrajnia taboru) A [m²]; Normalnotorowy tabor ma przekrój A ≈10 [m²]; elektrowozy A_EL ≈11 [m²];

• współczynnik oporu aerodynamicznego C_x [1] uwzględniający (niejawnie, ilościowo) kształty powierzchni czołowej i końcowej oraz długość składu pociągu.

[N] (2.6)

Dla celów obliczeniowych, w praktyce kolejnictwa wzór (2.6) upraszcza się jeszcze bardziej, wprowadzając współczynnik C = C_x ⋅ρ/2; Jednakże prędkość ruchu pojazdu względem powietrza V uściśla się: V = V_jazdy ± V_wiatru; W centralnej Polsce średnia roczna prędkość wiatru czołowego wynosi ok. 3 [m/s]. Gęstość ρ powietrza zmienia się losowo w granicach kilkunastu procent w zależności od ciśnienia atmosferycznego i temperatury. Wpływ ciśnienia i temperatury na gęstość ρ zilustrowano rysunkiem 2.1.

Rysunek 2.1. Zależność gęstości powietrza od ciśnienia i temperatury.

Wzajemną relację tych wielkości opisuje następujący wzór:

(2.7)

gdzie: p - ciśnienie powietrza [HPa] = [10² ⋅N/m²]

T - temperatura [K] = [°C + 273]

Przyjmując średnią wartość roczną ciśnienia 1013 [HPa] i temperatury +15 [°C], możemy obliczyć ρ_śr ≈ 1,2264 [kg/m³]. Biorąc powyższe pod uwagę, wzór (2.6) możemy zapisać w uproszczonej postaci:

(2.8)

gdzie prędkość jazdy oznaczono jako V, zaś prędkość wiatru jako V_w. We wzorach, obowiązujących w zarządach kolejowych dla określonego taboru, w miejsce iloczynu 0,613⋅C_x, podaje się wypadkowy współczynnik C.

Należy podkreślić, że w miarę wzrostu prędkości jazdy V, wpływ prędkości wiatru maleje. Wynika to z przekształcenia ostatniego członu wzoru (2.8):

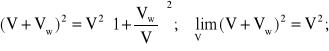
2.4. Opór wywołany dyssypacją energii ruchu pociągu w podtorzu [10].

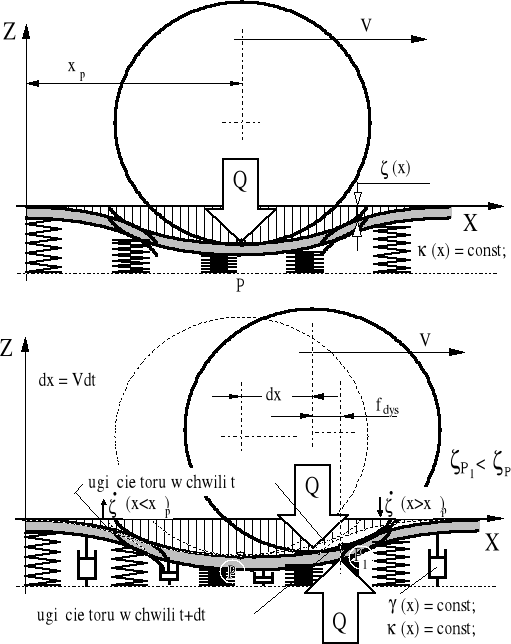
Rysunek 2.2. Ilustracja zjawiska wywołującego opór ruchu koła spowodowany tłumieniem w modelu toru i podtorza. Rysunek górny - tor sprężysty; rysunek dolny - tor sprężysto - plastyczny. Model przybliżony, nie uwzględniający zjawisk falowych.

Badania wykazały, że w bilansie oporów ruchu pojazdów szynowych zawsze występuje, ilościowo dość znaczący, człon liniowo zależny od prędkości pojazdu. Jest to wpływ wiskotycznych właściwości odkształceń podtorza. Zjawisko zilustrujemy na wielce uproszczonym przykładzie ustalonego ruchu koła z niewielką prędkością w wyidealizowanych warunkach.

Dynamiczne zjawiska falowe w systemie koło pojazdu - szyna, przy takich założeniach możemy pominąć. Na rysunku 2.2 pokazano dwa przypadki ruchu. Część górna ilustruje ruch sztywnego koła po nieważkiej szynie stanowiącej sprężyście odkształcalną belkę opartą na podłożu sprężystym; rysunek dolny - ruch tego samego koła po sprężystej belce opartej na podłożu lepko - sprężystym.

W pierwszym przypadku nacisk Q koła wywołuje odkształcenie toru symetryczne względem punktu styku. W punkcie styku P występuje ugięcie szyny (x=x_P) = _P, zaś nachylenie (wzniesienie / spadek) szyny jest zerowe:

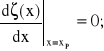
Pod działaniem nacisku koła Q, pole ugięć (zakreskowane) porusza się wraz z punktem P. Traktując sztywność wstęgi toru  [N/m²] jako niezmienną wzdłuż drogi, możemy napisać następujący warunek równowagi sił pozwalający doświadczalnie wyznaczyć wartość :

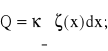
[N] (2.9)

gdzie całka opisuje pole ugięcia wstęgi toru [m²]; (x) - bieżąca wartość ugięcia szyny [m].

Sztywność statyczna wstęgi szyny zredukowana do punktu styku P (sztywność zastępcza) _P wynosi:

(2.10)

Na torze idealnie sprężystym nie występują opory ruchu zależne liniowo od prędkości.

W drugim przypadku przemieszczeniu koła o wielkość dx towarzyszy zmiana położenia linii ugięcia. Prędkość pionowa ugięć dowolnego punktu wstęgi szyny jest opisana wielkością
. Ponieważ:

(2.11)

to prędkość ugięcia w otoczeniu punktu jej styku z kołem zależy liniowo od prędkości V przemieszczania się punktu P wzdłuż szyny. System torowy więc, według badań eksperymentalnych, wykazuje znaczący (mierzalny) udział dyssypacji wiskotycznej. Współczynnik γ_t [Ns/m²] opisuje stosunek siły reakcji jednego metra bieżącego wstęgi nieważkiej szyny spoczywającej na podłożu sprężysto - plastycznym na ugięcia punktu P z prędkością 1[m/s].

Podczas ruchu koła wzdłuż szyny, jej wstęga przed kołem ugina się z opóźnieniem i podobnie z opóźnieniem powstaje za kołem. Koło, podobnie jak motorówka, porusza się jakby stale „pod górę”, pozostając jednak w zagłębieniu ugiętej szyny.

Koło, tocząc się z prędkością V po ugiętej wstędze szyny, ma do pokonania siłę F_γt, pochodzącą od tłumiącego przeciwdziałania podłoża.

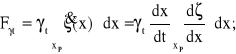
(2.12)

Należy w tym miejscu zauważyć, że:

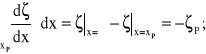
(2.13)

Dla skończonych wartości d/dx, występujących w przedmiocie rozważań, opór ruchu W_γt możemy zapisać następującym wzorem:

(2.14)

gdzie _P - wyznacza się doświadczalnie, statycznie, według wzoru (2.10).

2.5. Opór wywołany dyssypacją energii w zawieszeniu pojazdu [10] [11][12].

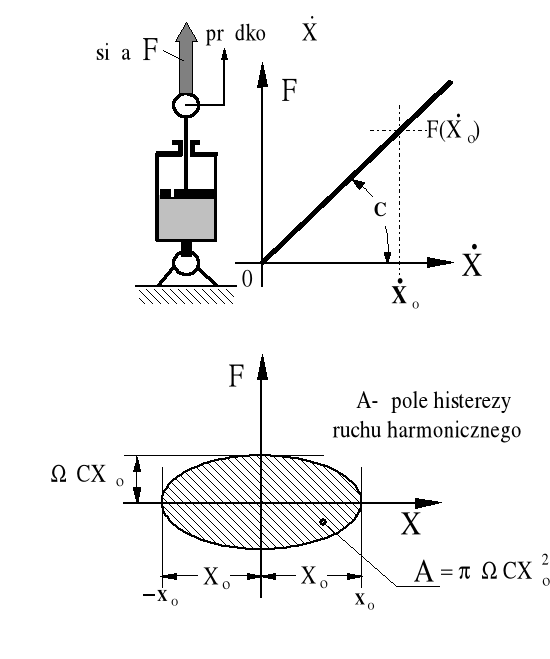
Rysunek 2.3. Zasada pracy tłumika wiskotycznego o charakterystyce liniowej.

A - pole pętli histerezy przy harmonicznych przemieszczeniach narzuconych na tłumik z ustaloną częstością kołową i amplitudą R=Xo.

Podstawowe zależności dotyczące dyssypacji energii w tłumiku hydraulicznym, są następujące:

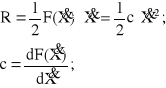
(2.15)

c - współczynnik tłumienia drgań;

R - funkcja Rayleigha (moc rozpraszania energii);

Podczas badania charakterystyki na urządzeniu zapewniającym ruch harmoniczny, otrzymamy wykres w postaci elipsy o półosiach odpowiednio: rzędna = a, odcięta = b; Pole elipsy S_E = πab; Dla ruchu harmonicznego możemy napisać:

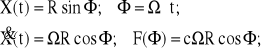
(2.16)

Praca siły F przypadająca w ruchu ustalonym z prędkością na 1/4 obrotu wynosi:

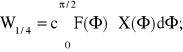
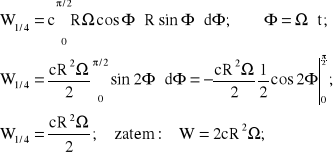
(2.17)

Praca W siły F, przypadająca na 1 okres (obrót), wynosi W = 2cR²;

Fizycznie jest to iloczyn uśrednionej (za 1 obrót) wartości siły F_śr i drogi (długości obwodu). Praca siły F przypadająca na 1 okres (obrót) odpowiada więc przebytej drodze 2R; zatem średnia wartość siły oporu dyssypacji wynosi:

(2.18)

Uśredniona siła oporu dyssypacji w zawieszeniu podwozia jest liniowo zależna od prędkości ruchu pojazdu szynowego V.

Podczas eksperymentalnych badań oporów ruchu składu pociągu, prowadzonych dla celów eksploatacji kolejowej, najczęściej ustala się współczynnik dyssypacji w zawieszeniu ściśle określonego taboru na określonym torze tak, że nie ma konieczności oddzielnego badania dyssypacji toru i podwozia pojazdu. Tłumiki podwozi bada się oddzielnie na stanowiskach.

Liniowo zależna od prędkości jazdy składowa wiskotycznych oporów ruchu pochodząca od pracy wszystkich tłumików pracujących w podwoziu pojazdu (lub całego pociągu) może być wyznaczona poprzez funkcję Raileigh'a czyli moc rozpraszania energii drgań:

(2.19)

R - funkcja Raileigh'a [Nm/s],

p - zastępczy (reprezentatywny, uśredniony) współczynnik trakcyjnego oporu wiskotycznego wszystkich tłumików pojazdu (pociągu) [Ns/m],

V - prędkość jazdy pociągu [m/s].

przy czym:

Wp = pV oraz W = Wt + Wp (2.20)

gdzie indeks "t" dotyczy toru (podtorza), "p" - pojazdu (pociągu).

Dla wszystkich tłumików w pojeździe, przy dostatecznie dużym czasie T obserwacji procesu i jego całkowego uśredniania, możemy napisać:

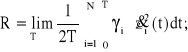
(2.21)

i - współczynnik tłumienia i-tego tłumika [Ns/m],

- prędkość tłoczyska w i-tym tłumiku [m/s],

N - liczba tłumików,

T - czas obserwacji procesu jazdy pojazdu (pociągu) z ustaloną prędkością V.

Na mocy powyższych wzorów możemy napisać:

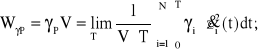
(2.22)

W praktycznym ujęciu wzorów empirycznych, składową oporu ruchu W, liniowo zależną od prędkości jazdy, przedstawia się w postaci iloczynu CV, gdzie uśredniona dla składu pociągu wartość

(2.23)

Wartość liczbową współczynnika C_γ wyznacza się na podstawie pomiarów doświadczalnych.

2.6. Uwzględnienie pracy prądnic wagonowych [1],[5],[10].

Rosnące zapotrzebowanie energetyczne nowoczesnego taboru pasażerskiego zmusza wytwórców do instalowania prądnic o coraz większej mocy. Prądnice te są napędzane od osi wagonowej. Moc nowoczesnej prądnicy wagonowej wynosi około 4,5 [kW]. Sprawność elektryczna prądnicy G wynosi ok. 0,85 zaś sprawność mechanicznego przeniesienia napędu m waha się w granicach od 0,75 do 0,9. Wygenerowanie mocy 4,5 [kW] obciąża zestaw mocą 5,7 - 7 [kW], co przy prędkości V = 35 [m/s] = 126 [km/h] wymaga dodatkowej siły WG, która stanowi składową oporu ruchu każdego wagony pasażerskiego. Według wyżej podanych wartości siła ta waha się w granicach 168 - 200 [N]. Jest to wartość niemal dwukrotnie przewyższająca mechaniczny opór toczenia się kół obciążonego wagonu po szynach (bez uwzględniania oporów aerodynamicz-nych).

(2.24)

2.7. Wypadkowy opór zasadniczy pociągu

Opór ten stanowi sumę:

- oporów kontaktowych łącznych według wzoru (2.2),

- oporu łożysk osiowych według wzoru (2.4),

- oporu aerodynamicznego według wzoru (2.8),

- oporu dyssypacji energii według wzorów (2.14), (2.20), (2.22).

Wzas = Wk + W Ł + W + WA (2.25)

przy czym (Wk + W Ł) = const; W = W(V); WA = WA(V2).

Zgodnie z wyżej omówionymi fizycznymi aspektami poszczególnych składowych oporu ruchu pociągu, wzór (poprzedni) można zapisać w postaci wielomianu:

Wzas = (a+bV)Q + cA(V+Vw)2; (2.26)

albo bardziej ogólnie: Wzas = AQ + BV +DV2; D=c⋅A; (2.27)

Mówiąc o wypadkowym oporze zasadniczym pociągu należy podkreślić, że:

W ruchu przyspieszonym i ustalonym pojazdu trakcyjnego siły odniesione do osi zestawów napędnych są większe od sił przyczepności.

W przypadku elektrodynamicznego hamowania pojazdu trakcyjnego siły odniesione do osi zestawów hamujących są mniejsze od sił przyczepności.

Podczas badania własnych oporów ruchu pojazdu trakcyjnego - odniesionych do osi jego zestawów - metodą pomiaru siły "na haku" należy (tuż przy zestawach) rozłączyć przekładnie mechaniczne jakie znajdują się pomiędzy silnikami trakcyjnymi a zestawami napędnymi tego pojazdu.

Charakterystyki pojazdów trakcyjnych najczęściej sporządza się w odniesieniu do osi ich zestawów napędnych.

Wzory opisujące opory ruchu pojazdów trakcyjnych najczęściej sporządza się w odniesieniu do osi ich zestawów napędnych.

Wzory opisujące opory ruchu pojazdów doczepnych sporządza się w odniesieniu do urządzeń cięgłowo - zderznych.

2.8. Wybrane wzory szczegółowe opisujące opory ruchu:

- Wzór Strahla dla lokomotyw normalnotorowych:

WoL = anQn + atQt + CA(V+Vw)2 [N];

gdzie:

Qn, Qt - naciski na tor zestawów - odpowiednio - napędnych i tocznych [kN],

an, at - współczynniki oporu toczenia zestawów napędnych i tocznych [N/kN]; an= 2,5 3,5; at = 1,8 3; wartości wyższe dla wózków trzyosiowych,

A - przekrój poprzeczny lokomotywy. Dla taboru normalnotorowego przyjmuje się A = 10 11 [m2]; wartości wyższe dla taboru z pantografem.

C - współczynnik oporu aerodynamicznego. Dla lokomotyw elektrycznych

C = Cel = 0,635; dla lokomotyw spalinowych C = Csp = 0,38; Przy dobrze oprofilowanych powierzchniach czołowych wartość współczynnika obniża się ok. 20%.

- Wzór CNTK dla lokomotyw PKP:

WoL = (0,9 + 0,054V)QL + 147n + 4,45V2 [N];

gdzie: QL - nacisk lokomotywy na tor [kN], n - liczba osi lokomotywy,

V - prędkość jazdy lokomotywy [m/s].

- Wzór CNTK dla zespołów trakcyjnych:

Wozt = (0,65 + 0,054V)Q + 147n + (2,7 + z)1,271V2 [N];

gdzie: Q - nacisk ładownego zespołu trakcyjnego na tor [kN], z - liczba wagonów w zespole trakcyjnym, n - liczba osi w zespole trakcyjnym,

V - prędkość jazdy zespołu [m/s].

- Wzór kolei francuskich dla pociągu TGV do prędkości 83,3 [m/s];

pociąg o masie 192 [t], nacisk Q składu na tor 1883,52 [kN]:

Wozt = (0,748 + 0,0344V)Q + 3,63V2 [N];

- Wzór kolei japońskich dla pociągu TOKAIDO do prędkości 70 [m/s];

Wozt = (1,65 + 0,0864V)QnZn + (0,78 + 0,01V)QdZd + [3,56 + (Z-1)]V2 [N];

gdzie: indeksy "n" i "d" odnoszą się do wagonów napędnych i doczepnych,

Z - liczba wagonów w składzie pociągu.

- Wzór kolei niemieckich (Sauthoffa) dla 4-osiowych wagonów pasażerskich:

Ww = (1,5 + 0,09V)Q + 0,885(2,7 + Z)(V+Vw)2 [N];

Vw - prędkość wiatru; w Europie środkowej średnio 2,7 - 4,2 [m/s].

- Wzór kolei niemieckich dla pociągów pasażerskich prowadzonych lokomotywą:

Wpoc = 3QL+1,59ALV2+1,5Qw+0,09QV+0,0763(m+2)Aw(V+4,17)2 [N];

gdzie: m - liczba wagonów; indeksy odnoszą się: L - do lokomotywy; W - do wagonów.

- Wzór Strahla dla wagonów towarowych:

Ww = [a + 0,1296(0,007 + m)V2]Qw [N];

gdzie a - współczynnik oporu łożysk i toczenia się kół po szynach [N/kN]; w taborze normalnotorowym przyjmuje się a = 1,7; m - współczynnik zależny od rodzaju pociągu (według tabeli). Prędkość jazdy V [m/s].

Tabela 2.1. Wartości współczynnika m oporu ruchu wagonów towarowych

RODZAJ SKŁADU WAGONOWEGO	m
Węglarki załadowane	0,025
Wagony kryte, ruch przyśpieszony	0,04
Skład mieszany (różne wagony)	0,05
Węglarki próżne	0,10

Warto zwrócić uwagę na to, że we wzorze Strahla dla wagonów towarowych, które nie mają tłumików hydraulicznych w zawieszeniu, nie występuje - liniowo zależny od prędkości jazdy - człon oporu ruchu składu.

2.9. Opór dodatkowy ruchu pociągu [13].

♦ Opór ruchu pociągu przy pokonywaniu wzniesień

Opór pojawiający się przy pokonywaniu wzniesień „i” [%o] ma oddziaływanie superpozycyjne z oporami zasadniczymi. Opór ten, w polu grawitacyjnym, wyznacza się metodą elementarną zgodnie z rysunkiem 2.4.

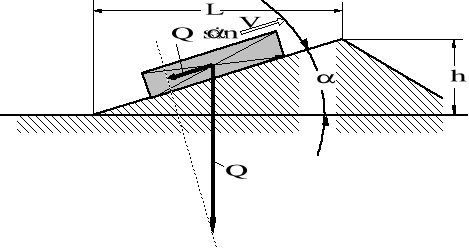
Rysunek 2.4. Szkic pomocniczy do wyznaczenia oporu wzniesienia.

(2.28)

Ponieważ w kolejowej trakcji adhezyjnej największe wzniesienia nie przekraczają 1^°43'= 0,03 [rad] = 30 [%o], to możemy przyjąć w przybliżeniu:

(2.29)

W przypadku gdy „h” wyrazimy w metrach zaś „L” w kilometrach, to pochylenie sin  ≈ tg  możemy opisywać w promilach [%o], czyli w [m/km]. Przy takim podejściu wzór (31) przekształca się do następującej postaci:

gdy nacisk Q jest wyrażony w niutonach albo

(2.30)

gdy nacisk Q jest wyrażony w kiloniutonach.

Należy w tym miejscu zauważyć, że matematyczna ścisłość opisu oporu wzniesień zgodnie z (33), dotyczy jedynie przypadku, gdy cały skład pociągu znajduje się na jednakowym wzniesieniu. W kolejnictwie takie przypadki zdarzają się sporadycznie. Z tej przyczyny, dla dowolnego położenia składu pociągu na pochyleniach szlaku, wyznacza się tak zwany profil zastępczy toru, który uwzględnia zarówno rzeczywistą rzeźbę geodezyjną szlaku jak też długość składu pociągu. Szczególną skrupulatność w tym zakresie należy przejawiać w odniesieniu do długich składów wolnobieżnych pociągów towarowych.

Opór ustalonego ruchu składu pociągu, pracującego w ruchu szybkobieżnym, charakteryzującego się dużymi wartościami energii kinetycznej, jest tak znaczny, zwłaszcza z przyczyn aerodynamicznych, że wpływ dodatkowego oporu wzniesień jest stosunkowo niewielki.

♦ Opór ruchu pociągu w krzywiznach toru [10],[13].

Badania wykazały, że w obrębie krzywizny toru pociąg napotyka dodatkowy opór, którego wartość jest niemal liniowo proporcjonalna do nacisku pojazdu na tor i odwrotnie proporcjonalna do promienia krzywizny. Bezluzowe konstrukcje prowadników osi zestawów o dużej sztywności podłużnej względem ramy sprawiają, że w łukach toru występują znaczne wartości kątów nabiegania kół na szyny, poślizgi wiertne w rejonie obrzeża oraz poślizgi podłużne kół po szynach. W literaturze szeroko cytowany jest wzór Röckla:

(2.31)

Wzór (34) wykazuje dobrą zgodność z rzeczywistością pomiarową przy wartościach promieni R ≥ 350 [m]. Nacisk Q jest przy tym wyrażony w [kN] zaś współczynnik a w [Nm/kN]. W torze normalnym (UIC) obowiązują następujące wartości tego współczynnika:

• dla wagonów dwuosiowych a = 650,

• dla wagonów czteroosiowych a = 370,

Dla pracujących na torach UIC (1435 mm) wagonów ramowych ze sztywnymi prowadnikami osi przyjmuje się wzór Franka:

(2.32)

gdzie l - rozstawienie skrajnych osi w sztywnej ramie [m], Q - nacisk pojazdu na tor [kN], R - promień krzywizny toru [m]; m - współczynnik: dla pociągów towarowych m = 2000, dla pasażerskich m = 1000.

Dla kolei wąskotorowych obowiązuje wzór Hillera:

(2.33)

gdzie s - szerokość toru [m]; pozostałe oznaczenia jak dla wzoru (35).

Podobny zakres zastosowań ma wzór Langroda:

(2.34)

według oznaczeń opisanych powyżej.

W przypadku, gdy skład pociągu znajduje się w torze o zmiennej krzywiźnie, opór dodatkowy składu należy obliczać jako sumę oporów częściowych przy potraktowaniu znaków wszystkich promieni krzywizny jako dodatnie. Przy składzie niejednolitym, (niejednakowe wagony) podobnie: łączne opory dodatkowe oblicza się jako sumę oporów składowych. Przy wyznaczaniu wartości oporów dodatkowych pociągu w rozjazdach, wygodniej jest operować pojęciem oporu jednostkowego w_Ri=W_i/Q_i [N/kN]. Wtedy średnia wartość oporu dodatkowego, odnosząca się do całego składu pociągu, wynosi:

(2.35)

gdzie l_i - długość pojedynczego rozjazdu o promieniu R_i [m], L - długość składu pociągu [m].

2.10. Zasady doświadczalnego badania oporów ruchu pociągu [10].

Celem doświadczalnego badania oporów ruchu pociągu jest eksperymentalna identyfikacja wartości współczynników a, b i c we wzorze (2.26) lub A, B i C we wzorze (2.27).

W przypadku badań oporów ruchu pociągów prowadzonych przez lokomotywę, badania oporów lokomotywy i składu wagonowego prowadzi się oddzielnie.

Ogólnie, wyróżnia się dwie metody badawcze:

• metodę bezpośredniego pomiaru siły trakcyjnej (pociągowej lub pchającej) przy zadanej i ustalonej prędkości jazdy (metoda Sauthoffa), oraz:

• metodę „wybiegu” na podstawie zarejestrowanych parametrów bezwładnego ruchu pojazdu od prędkości maksymalnej aż do zatrzymania.

Pierwszą z nich stosuje się przede wszystkim do badania wagonów, często też do badania oporu ruchu lokomotyw; drugą z nich - z zasady - do badania oporów ruchu zespołów trakcyjnych. W metodzie pierwszej korzysta się z dodatkowej lokomotywy oraz wagonu dynamometrycznego. W metodzie drugiej zespół trakcyjny rozpędza się do prędkości maksymalnej za pomocą napędu własnego. Aparatura pomiarowa jest umieszczona w badanym składzie.

Do badań metodą pomiaru bezpośredniego siły trakcyjnej należy wybrać odcinek toru prostego o stałej wartości nachylenia (spadku), stabilną temperaturę (ze względu na gęstość powietrza) i stałą prędkość wiatru o kierunku zgodnym z kierunkiem toru, z dokładnością do około 0,1 [rad]. Podczas badań lokomotywy jej przekładnie powinny być rozłączone tuż przy zestawach. Przy stałych, lecz kolejno różnych, prędkościach realizuje się pary przejazdów „tam' i „z powrotem”.

Przy badaniach metodą „wybiegu” tor (najkorzystniej) powinien być prosty i poziomy. Realizuje się co najmniej jedną parę przejazdów „tam' i „z powrotem” rejestrując konieczne parametry w dziedzinie czasu.

2.11. Zarys metodyki badania oporów ruchu pociągu według Sauthoffa [10]

Metoda Sauthoffa jest metodą bezpośredniego pomiaru siły pociągowej (lub pchającej) przy zadanej prędkości jazdy, przy użyciu urządzeń pomiarowych i rejestracyjnych stanowiących wyposażenie wagonu pomiarowego.

Sygnał siły na urządzeniu pociągowo - zderznym F_h = W_poc rejestruje się w funkcji drogi lub / oraz czasu. Badany pociąg, wraz z wagonem dynamometrycznym, jest prowadzony dodatkową lokomotywą.

Sauthoff, jako pierwszy, wprowadził oryginalną zasadę „podwójnych jazd”: „tam” [T] i „z powrotem” [P], na tym samym odcinku toru prostego, o stałym wzniesieniu, z takimi samymi prędkościami V_poc, możliwie przy tej samej prędkości wiatru V_wiatru, którego kierunek powinien być zbliżony do kierunku toru, z dokładnością do ok. 5^o.

Najprostsza, najogólniej pojmowana, wielomianowa postać wzoru opisującego opór ruchu pociągu na torze prostym i poziomym, jest następująca:

(2.36a)

Bardziej szczegółowa, dość powszechnie stosowana, postać tego wzoru, uwzględniająca wyartykułowane wartości prędkości wiatru i wzniesienia toru, jest następująca:

(2.36b)

W celu szczegółowej identyfikacji współczynników A, B i C wzoru (2.36a) w istniejących warunkach geodezyjnych i atmosferycznych, Sauthoff przyjął bardziej rozwiniętą postać wzoru (2.36b), uwzględniającą opory wzniesienia i[%o] oraz udział prędkości wiatru w oporach aerodynamicznych pociągu

V=V_poc ± V_wiatru.

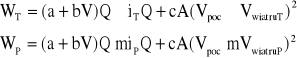
(2.37)

W zapisie (2.37) przyjęto, że występująca niejawnie we współczynniku c, gęstość powietrza ρ, podczas podwójnej jazdy, nie zmienia się. W przypadku szybkich zmian ciśnienia i temperatury powietrza powyższe wzory należy skorygować odpowiednio wprowadzając gęstości ρ_T i ρ_P.

Oznaczenia: Q [N] - nacisk grawitacyjny badanego składu na tor; Q=Mg;

A [m²] - powierzchnia poprzecznego przekroju taboru (skrajnia taboru).

Odejmując stronami (2.37), dla przypadku i_T > 0, i_T = −i_P;

V_wiatruT > 0, V_wiatruP = −V_wiatruT, otrzymujemy:

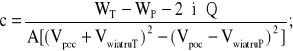
(2.38)

Wartość (stałego) współczynnika oporu aerodynamicznego c, w ujęciu wzoru (2.38), powinna być niezależna od prędkości jazdy badanego pociągu. W celu uściślenia poprawnej wartości tego współczynnika, otrzymanej według powyższego wzoru z nieuniknionym błędem pomiarowym, należy badanie powtórzyć przy zmienionej prędkości pociągu. W praktyce wykonuje się kilka par jazd „tam” [T] i „z powrotem” [P]. Wartość współczynnika „c” jest wynikiem uśrednienia. Mając zidentyfikowaną wartość współczynnika c, na podstawie zarejestrowanych wyników pomiarów dwóch kolejnych par jazd z prędkościami V₁ i V₂, wyznaczamy wartości współczynników a i b.

Dodając stronami równania (2.37), otrzymujemy jedną postać równania algebraicznego dla dwóch prędkości. Dla przypadku jak wyżej, na mocy wyników pomiarów dwóch kolejnych par jazd z prędkościami V₁ i V₂, eliminujemy wpływ wzniesień (i spadków) toru na odcinku pomiarowym:

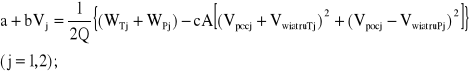
(2.39)

Z powyższych dwóch równań wyznaczamy wartości współczynników a i b, gdyż wszystkie wielkości występujące po prawej stronie znaku równości, dla prędkości V₁ i V₂, są zarejestrowane lub obliczone, a więc znane.

Praktyczna użyteczność zidentyfikowanego zapisu (2.36b) dodatkowo rośnie, gdy we współczynniku c uwzględni się długość pociągu lub liczbę wagonów (jeśli są jednakowe). Aby uzyskać dodatkowe informacje należy ponownie przeprowadzić wyżej opisane badania lecz z inną - niż poprzednio - liczbą wagonów (np. zmniejszoną o połowę).

Wyrażając współczynnik c jako liniową funkcję długości l składu, to dla dwóch długości składu l₁ i l₂, możemy napisać:

(2.40)

skąd bezpośrednio wyznaczamy:

(2.41)

Ogólnie więc zapis c (2.36b) możemy przedstawić jako:

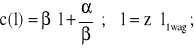
(2.42)

2.12. Badanie oporów ruchu metodą „wybiegu” czyli biegu z rozpędu aż do zatrzymania [10].

Rys. 2.5. Szkic pomocniczy ilustrujący ruch składu aż do zatrzymania.

Przyspieszenia w przedziałach ΔV_j wyznacza się przy stałym przedziale czasowym Δt według zasady:

(2.43)

Charakterystyka zależnych od wartości wzniesienia “i” [%o] oporów ruchu ma następującą ogólną postać wykreślną i analityczną:

Rys. 2.6. Charakter oporów ruchu składu na wzniesieniu

[N] (2.44)

Dla każdego j-tego punktu można sporządzić zapis oporów ruchu zasadniczego w ujęciu jednostkowym:

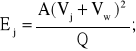
(2.45)

Minimalna liczba punktów pomiarowo - obliczeniowych „n” nie może być mniejsza od liczby (trzech) współczynników w równaniu (2.36): (j=1,2,...n); n≥3; Wartości pomiarowe w tych punktach wyznacza się obliczeniowo na podstawie zarejestrowanego przebiegu V(t), odpowiednio posługując się przebiegiem a_j(t), obliczonym według (2.36) w wybranych przedziałach prędkości „j”.

W ten sposób, każdemu j-temu przedziałowi prędkości przyporządkowuje się przyśpieszenie. Znając wszystkie n wartości przyśpieszeń a_j możemy wyznaczyć wartości siły całkowitych oporów ruchu, według (2.37), podczas jazdy w obydwóch kierunkach zarówno dla i_T [%o] jak też i_P. W ten sposób otrzymujemy co najmniej 6 wartości oporów ruchu odpowiadających 6 punktom według rysunku 2.

Związek oporów ruchu W_jT i W_jP w j-tym przedziale prędkości z wartością (zawsze ujemnego) przyśpieszenia a_j (podczas jazdy w obydwóch kierunkach „T - tam” oraz „P - z powrotem”) jest następujący:

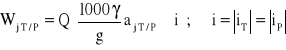
(2.46)

Odejmując stronami dwie postacie równania (2.46) odpowiednio dla kierunków „T” i „P”, eliminuje się wpływ wzniesienia.

Na mocy równań (2.47) zapisanych dla trzech, odpowiednio od siebie oddalonych, przedziałów prędkości V₁, V₂ i V₃, możemy wyznaczyć wartości współczynników A, B i C:

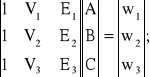
(2.47)

gdzie w_j = w_{zas j};

Celem badań jest wyznaczenie oporów ruchu pojazdu w funkcji prędkości. Jednakże łatwo możemy podczas badań zmierzyć każdorazowo drogę na jakiej pojazd zatrzymał się po jeździe w obydwóch kierunkach. Jeżeli badanie jest prowadzone na niewielkim wzniesieniu, przy ustalonym wietrze o znanej prędkości, skierowanym wzdłuż toru, to czas do zatrzymania składu (od takiej samej prędkości początkowej) będzie za każdym razem inny.

Obliczeniową wartość drogi s(t) traktujemy jako czynnik kontroli poprawności procesu pomiarowego i obliczeniowego z wartością zmierzoną:

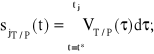
(2.48)

2.13. Aproksymacyjna metoda najmniejszych kwadratów błędów w opracowywaniu wyników pomiarów [10].

Aproksymacyjna metoda najmniejszych kwadratów błędów stanowi uogólnienie, na przypadek wielomianowy, metody wyznaczania wartości skutecznej RMS (Root Mean Square Value).

Przyjmijmy ogólną postać wielomianu m- tego stopnia, aproksymującego krzywą F(x):

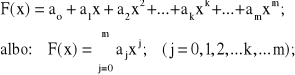
(2.49)

Krzywa F(x) ma aproksymować, w sposób ciągły, przebieg procesu zarejestrowanego w postaci n dyskretnych wartości pomiarowych Zi(x); (i=1,2,3,...n) przy czym liczba n wartości pomiarowych musi być większa od stopnia m wielomianu.

n > m (2.50)

Ogólnie znana zarówno w statystyce matematycznej jak i w technice pomiarowej wartość skuteczna RMS jest pierwiastkiem wartości średniokwadratowej, czyli momentu rzędu drugiego. Jej cechą jest to, że średnie odchylenie standardowe (będące pierwiastkiem wariancji czyli momentu centralnego rzędu drugiego) względem wartości RMS, jest zerowe. Uogólniając pojęcie wartości skutecznej do dziedziny funkcji (wielomianu), należy zapewnić minimalizację sumy kwadratów błędów. Taką sumę możemy zapisać następująco:

(2.51)

Błąd aproksymacji, ze względu na wspólczynnik ak wielomianu F(x) osiągnie minimum, gdy:

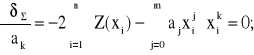
(2.52)

gdzie: i - liczba punktów pomiarowych (i=1,2,3,....n);

j - stopień wielomianu aproksymującego (j=0,1,2,...k,...m);

Wyrażenie (2.51) możemy następująco przedstawić w rozwinięciu:

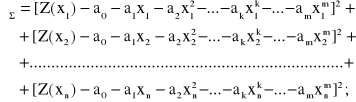
(2.53)

Kolejne operacje różniczkowania według (55) mają następującą postać:

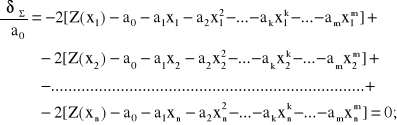
(2.54)

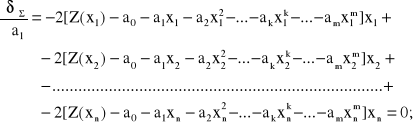
(2.55)

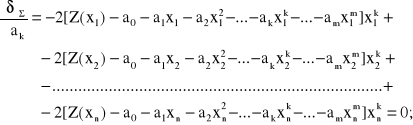
(2.56)

W wyniku odpowiedniego przemnożenia wyrazów w wierszach i kolumnowego zsumowania powyższych wyrażeń, otrzymujemy kolejno po uporządkowaniu:

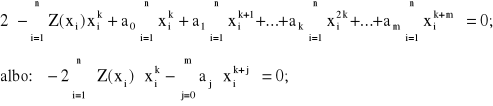
(2.57)

Ponieważ wielomian F(x), według (2.36), ma (m+1) współczynników, to w praktycznym przypadku, n ≥ m+1;

Dla kolejnych wartości k ∈ j, na podstawie (2.57) otrzymujemy (m+1) równań algebraicznych, z których wyznaczamy wartości współczynników aproksymacji aj.

2.14. Przykład obliczeniowy [10].

Wyznaczymy wartości współczynników A, B i C identyfikacyjnego wielomianu drugiego stopnia:

(2.58)

Rozwinięta postać odpowiednich równań w liczbie m+1=3, wynikająca wprost z górnego zapisu (2.57), kolejno dla k=0; k=1; oraz k=2; jest następująca:

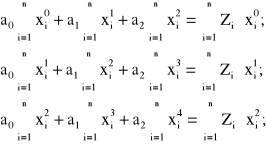
(2.59)

Podczas pomiaru zarejestrowano wartości parametrów według tabeli 2.2.

Tabela 2.2. Wartości zarejestrowane podczas pomiaru

Numer punktu	symbol "i"	1	2	3	4	5	6	7	8
Wartość V [m/s]	xi	10	20	30	40	50	60	70	80
Siła F=W [kN] oporów	Zi	12	20	30	43	60	80	103	130

dla k=0, otrzymujemy następujące wyrazy kolejnych równań (2.59):

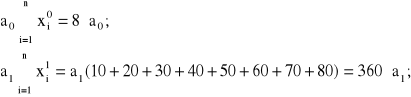
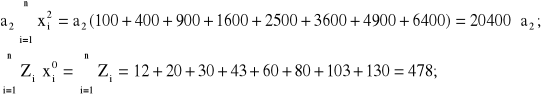
dla k=1, otrzymujemy następujące wyrazy kolejnych równań (2.59):

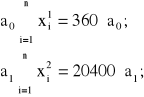
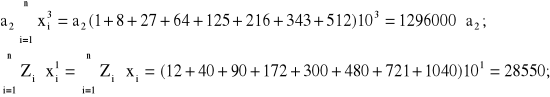
dla k=2, otrzymujemy następujące wyrazy kolejnych równań (2.59):

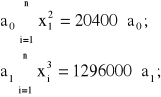
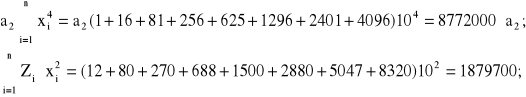
Podstawiając w dalszym ciągu a0=A; a1=B; a2=C; x=V, otrzymujemy ukad trzech równań algebraicznych względem jawnych współczynników wielomianu (2.58):

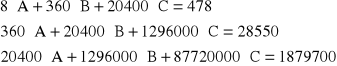
albo:

skąd bezpośrednio otrzymujemy: A=8,6097; B=0,21884; C=0,01619; zaś odpowiadające wyrażeniu (2.27) równanie aproksymacyjne z jawnymi współczynnikami, ma następującą postać:

Na podstawie powyższego wyrażenia obliczamy wartości wielomianu, które możemy porównać, z obarczonymi nieuniknionym błędem odczytu, wartościami pomiarowymi.

Tabela 2.3. Wartości aproksymowane na tle wartości pomiarowych

Numer punktu	1	2	3	4	5	6	7	8
Prędkość V [m/s]	10	20	30	40	50	60	70	80
Wartość W(V) [kN] aproksymacyjna	12,419	19,462	29,746	43,267	60,027	80,024	103,259	129,733
Wartość W [kN] pomiarowa	12	20	30	43	60	80	103	130

1

51

1,1

1,2

1,3

1,4

1,5

ρ kg/m³]

-5

0

5

10

20

15

T (°C)

920 [Hpa]

960 [Hpa]

1000

1040

1080 [Hpa]

760 [mm Hg] = 1013,25 [Hpa] = 101325 [N/m²]

OPORY RUCHU POCIĄGU

(dotyczy każdego pojazdu trakcji adhezyjnej)

POCHODZĄCE OD POJAZDU (ZASADNICZE)

POCHODZĄCE OD NAWIERZCHNI (NAWIERZCHNI)

AERODYNAMICZNE

MECHANICZNE

LEPKOŚĆ POWIETRZA

GĘSTOŚĆ POWIETRZA

KSZTAŁT POJAZDU I GŁADKOŚĆ

JEGO POWIERZCHNI

DŁUGOŚĆ POJAZDU

TARCIE W ŁOŻYSKACH

TOCZENIE KÓŁ PO NAWIERZCHNI

POŚLIZGI KONTAKTOWE KÓŁ

UDERZENIA KÓŁ W NIERÓWNOŚCI

DYSSYPACYJNE POCHODZĄCE OD

PRACY ZAWIESZENIA

DYSSYPACYJNE POCHODZĄCE OD

ODKSZTAŁCEŃ NAWIERZCHNI

POKONYWANIE WZNIESIEŃ

POKONYWANIE KRZYWIZN NA SZLAKU

KRZYWIZNY MANEWROWE

ΔV_j

t

V

V*

V_j

Δt

t_j

t*

V₁

V₂

V₃

V

W

i_T

i_P

---