1. Wstęp teoretyczny:

Odwrotność oporu nazywana jest przewodnictwem elektrycznym.

gdzie

π - przewodnictwo

R - opór

ρ - opór właściwy

q - przekrój przewodzącego słupa elektrolitu

l - długość przewodzącego słupa elektrolitu

k - przewodnictwo właściwe

Przewodnictwem właściwym nazywamy odwrotność oporu kostki sześciennej elektrolitu o długości krawędzi 1 cm. Ładunki elektryczne w elektrolicie przenoszą jony, wynika z tego, że tym większe jest przewodnictwo właściwe im większe jest stężenie jonów, oraz im większa jest szybkość jonów. Wynika z tego, że przewodnictwo właściwe jest zależne od stężenia elektrolitu oraz jego rodzaju.

W elektrochemii często jest stosowane pojęcie przewodnictwa równoważnikowego lub molowego λ, a związek przewodnictwa równoważnikowego z przewodnictwem właściwym przedstawia równanie:

gdzie

c - stężenie elektrolitu [grówn / l]

V = 1/c - rozcieńczenie, liczba litrów w których mieści się 1 grówn (lub 1 mol)

Związek pomiędzy przewodnictwem równoważnikowym, stopniem dysocjacji oraz ruchliwością jonów dla najprostszych przypadków dysocjacji przedstawiają równania:

λ = Fα(u_{a +} u_k)

dla c → 0 ; v → ∞ otrzymujemy λ₀ = F (u⁰_a + u⁰_k) .

gdzie

F - stała Faradaya (96500 C)

α - stopień dysocjacji.

Gdy podzielimy powyższe równania stronami otrzymujemy:

Otrzymane równanie jest wykorzystywane do obliczania stopnia dysocjacji w oparciu o pomiary przewodnictwa. W rzeczywistości w powyższy sposób można obliczyć iloczyn stopnia dysocjacji
i stosunku sum ruchliwości jonów.

Miareczkowanie konduktometryczne jest metodą polegającą na wyznaczaniu przewodnictwa właściwego roztworu, jako funkcji liczby mililitrów dodawanego stopniowo roztworu miareczkującego o znanym stężeniu.

W procesach elektrolizy przemysłowej bardzo duże znaczenie ma przewodnictwo elektryczne. Wraz ze wzrostem przewodnictwa właściwego można stosować coraz niższe napięcia, w celu uzyskania takiego samego natężenia prądu, dzięki czemu w znacznie mniejszym stopniu jest zużywana energia elektryczna. W procesach przemysłowych często do kąpieli elektrolitycznych dodaje się substancji nie biorących udziału w procesach elektrodowych, lecz zwiększających przewodnictwo kąpieli. Na przykład w procesie elektrorafinacji miedzi stosuje się dodatek kwasu siarkowego. Zwiększenie przewodnictwa roztworu można uzyskać także podwyższając tempera-turę, np. elektrorafinacja miedzi jest prowadzona w temperaturze ok. 50 ^oC .

Miareczkowanie konduktometryczne jest metodą bardzo przydatną do wyznaczania stężenia
w roztworach mętnych lub barwnych, podobnie jak w roztworach, dla których nie jesteśmy w stanie wskazać indykatorów mogących wskazać punkt zmiareczkowania.

2. Cel ćwiczenia:

• wyznaczenie przewodnictwa właściwego roztworów: CuSO₄, H₂SO₄ oraz CH₃COOH
  o różnych stężeniach oraz sporządzenie w oparciu o uzyskane wyniki wykresów: k = f(c),
  λ = f(V) , oraz α = f(c)

• wyznaczenie stężenia roztworu ZnCl₂ w oparciu o pomiar przewodnictwa oraz dane tabelaryczne

• wyznaczenie stężeń na drodze miareczkowania konduktometrycznego:

mocnego kwasu - mocną zasadą

słabego kwasu - mocną zasadą

3. Opracowanie wyników:

elektrolit	stężenie c [grówn/l]	stężenie c [mol/l]	przewod-nictwo właściwe k [S/cm]	tempera-tura [^oC]	przewod-nictwo molowe λ [S⋅cm^2/mol]	λ / λ0	rozcieńcze-nie V [dm^3/mol]
H2SO4 λ0 = 766,6 [S⋅cm^2/mol]	2,0	1,0	0,422	21,6	422	0,550483	1
		1,0	0,5	0,228	22,6	456	0,594834	2
		0,2	0,1	0,053	21,5	530	0,691364	10
		0,04	0,02	0,013	22,1	650	0,8479	50
		0,008	0,004	0,00333	22,5	832,5	1,085964	250
		0,0016	0,0008	0,00081	22,1	1012,5	1,320767	1250
	CH3COOH λ0 = 349,9 [S⋅cm^2/mol]	2,0	2,0	0,00174	21,3	0,87	0,002486	0,5
		1,0	1,0	0,00147	21,6	1,47	0,004201	1
		0,2	0,2	0,00074	21,4	3,7	0,010574	5
		0,04	0,04	0,00034	21,8	8,5	0,024293	25
		0,008	0,008	0,00015	21,5	18,75	0,053587	125
		0,0016	0,0016	0,0000665	21,6	41,56	0,118784	625
	CuSO4 λ0 = 227,2 [S⋅cm^2/mol]	2,0	1,0	0,0463	20,9	46,3	0,203785	1
		1,0	0,5	0,0295	21,7	59	0,259683	2
		0,2	0,1	0,0088	20,6	88	0,387324	10
		0,04	0,02	0,0025	20,5	125	0,550176	50
		0,008	0,004	0,000727	21,1	181,75	0,799956	250
		0,0016	0,0008	0,000191	20,8	238,75	1,050836	1250

Obliczanie stałej dysocjacji K dla kwasu octowego:

stężenie c [mol/l]	λ / λ0	stała dysocjacji K	stężenie c [mol/l]	stopień dysocjacji α	stała dysocjacji K
2,0	0,002486	1,24 ⋅ 10^-5	0,04	0,024293	2,42 ⋅ 10^-5
1,0	0,004201	1,77 ⋅ 10^-5	0,008	0,053587	2,43 ⋅ 10^-5
0,2	0,010574	2,26 ⋅ 10^-5	0,0016	0,118784	2,56 ⋅ 10^-5

Wyznaczamy K_śr = 2,11334 ⋅ 10^-5.

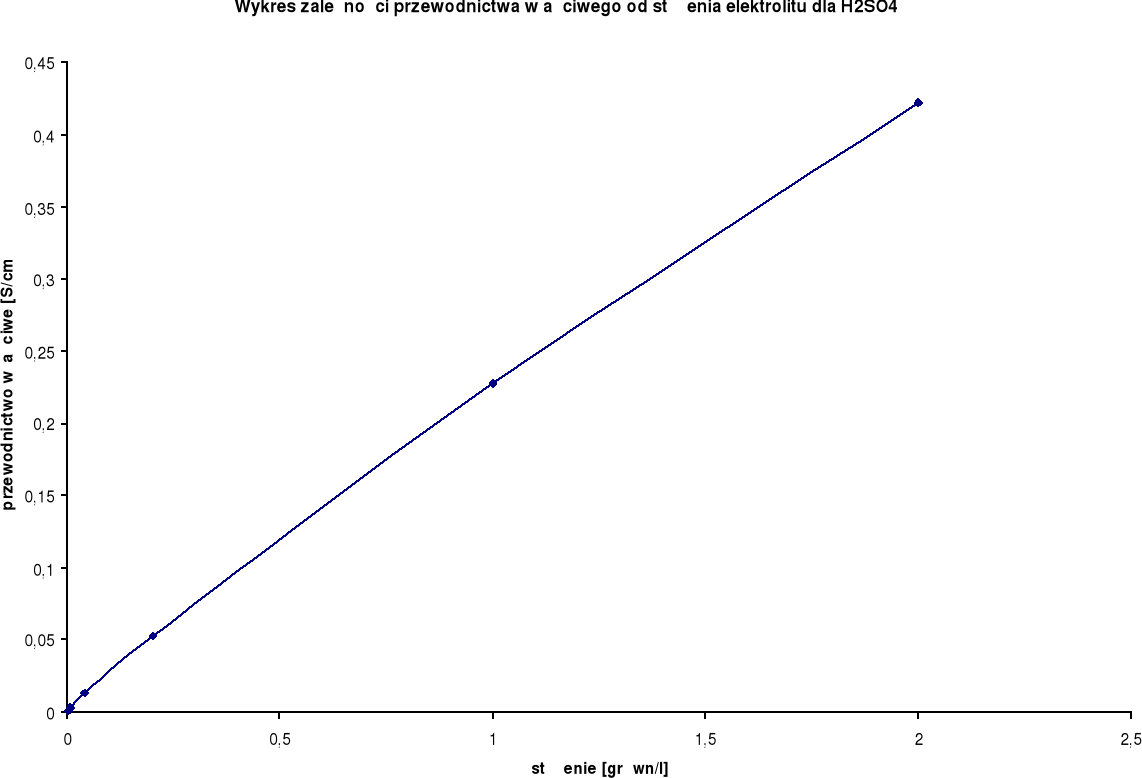
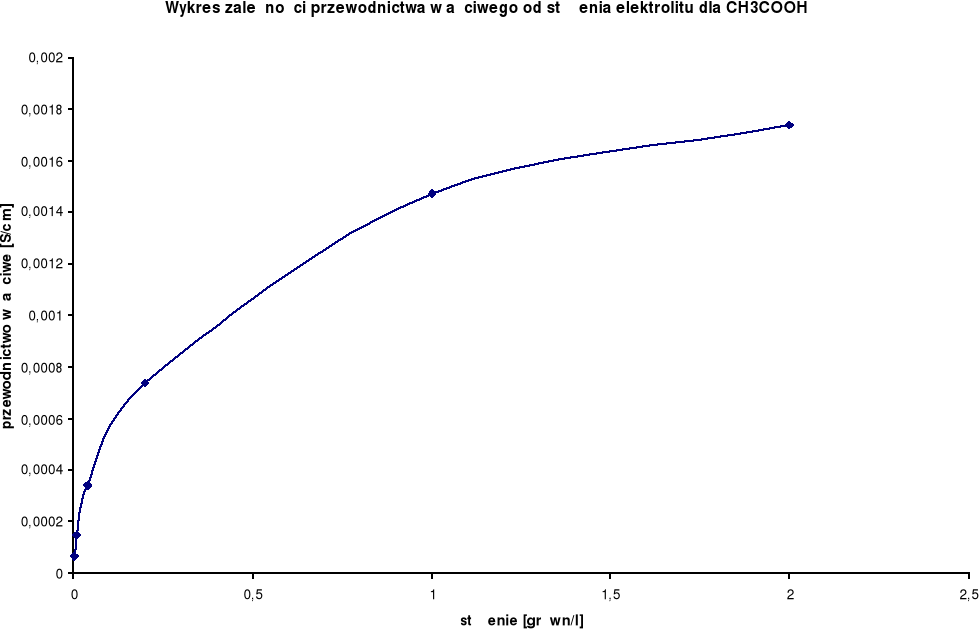
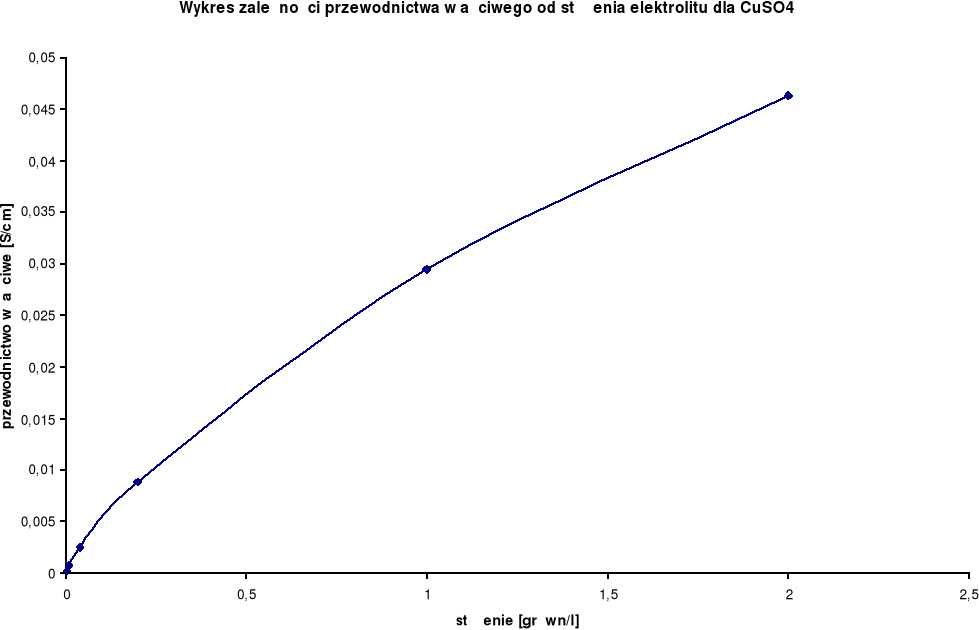
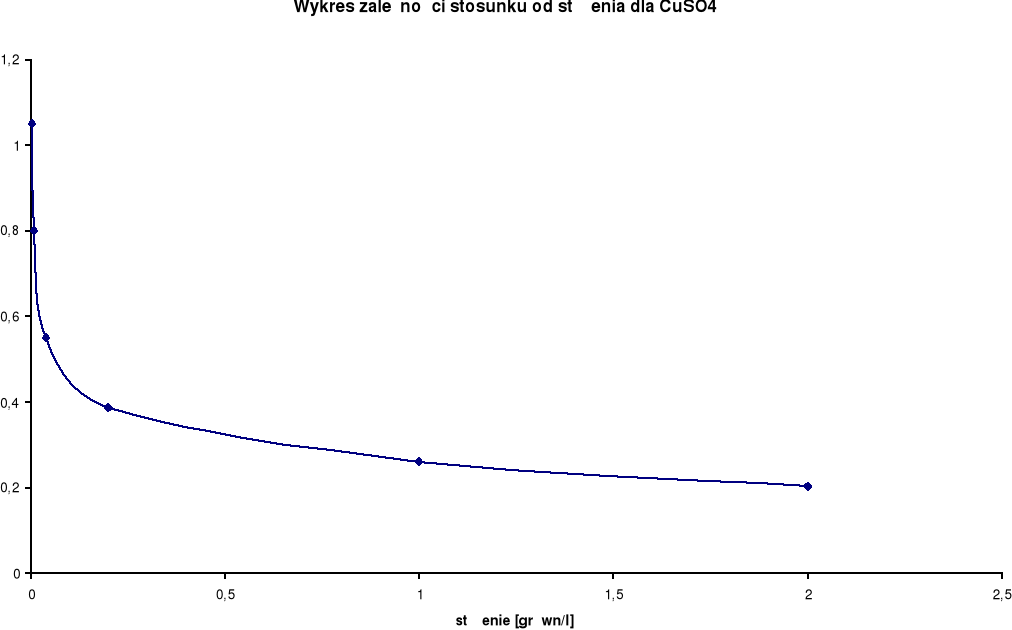
Wykresy zależności przewodnictwa właściwego od stężenia elektrolitu:

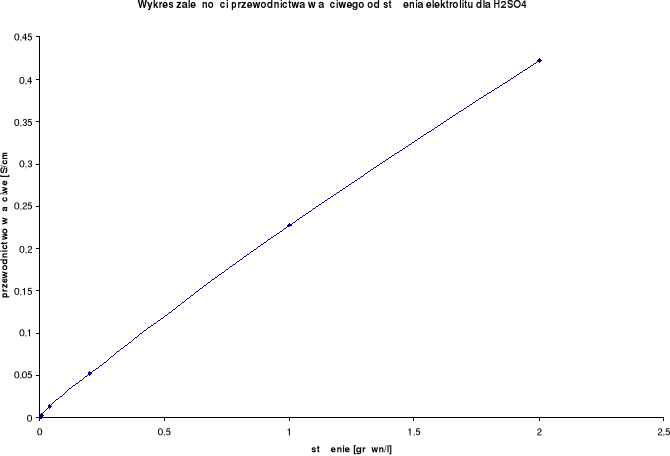
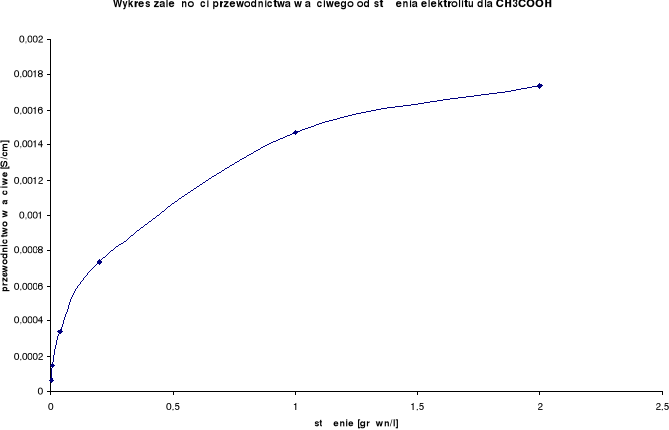
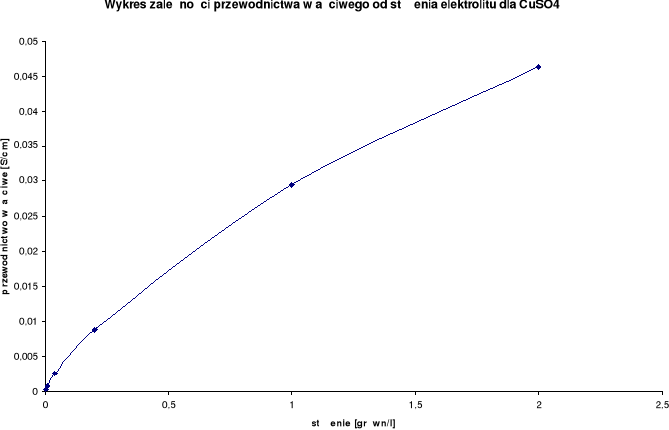
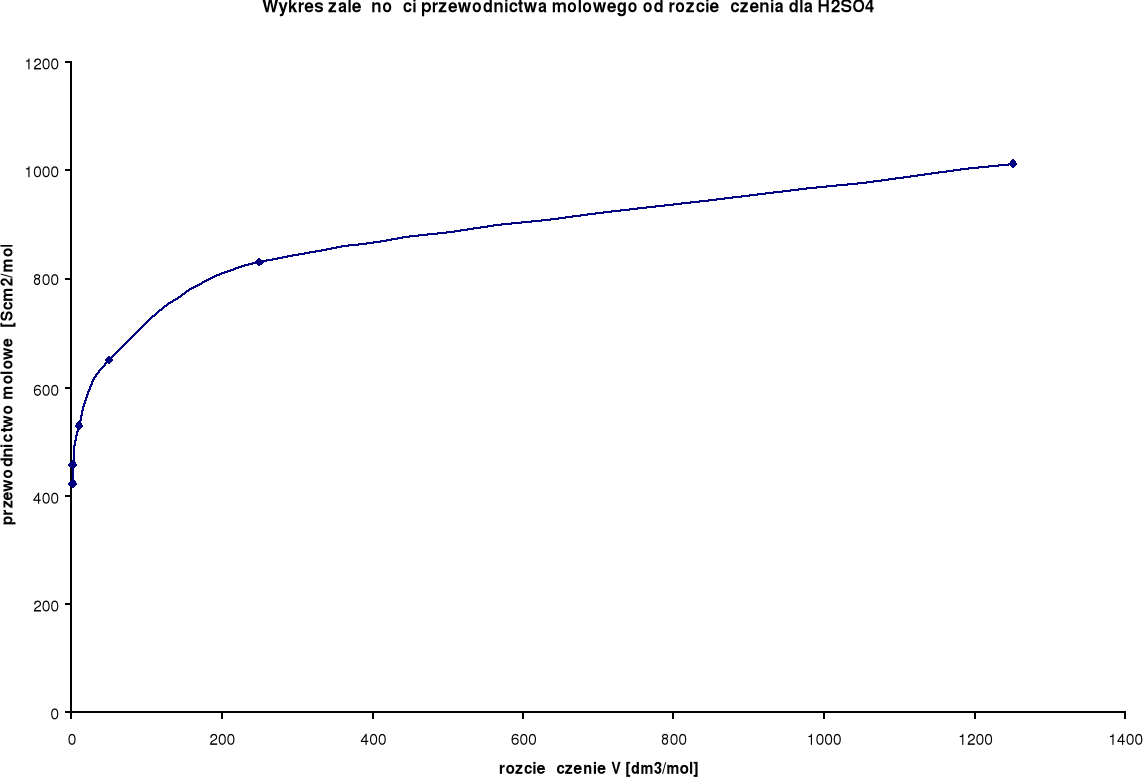
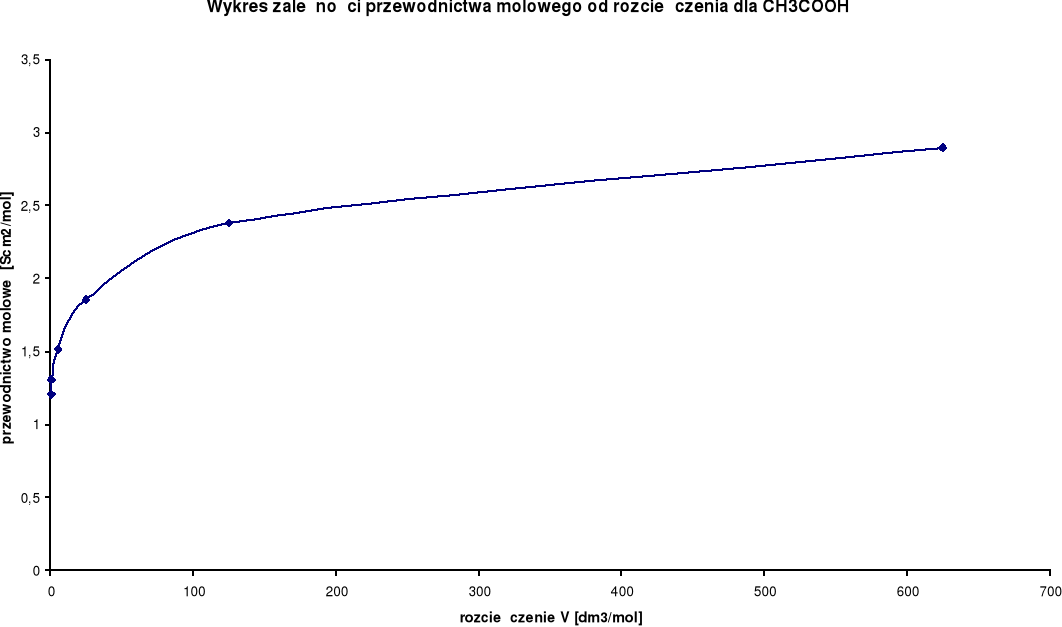
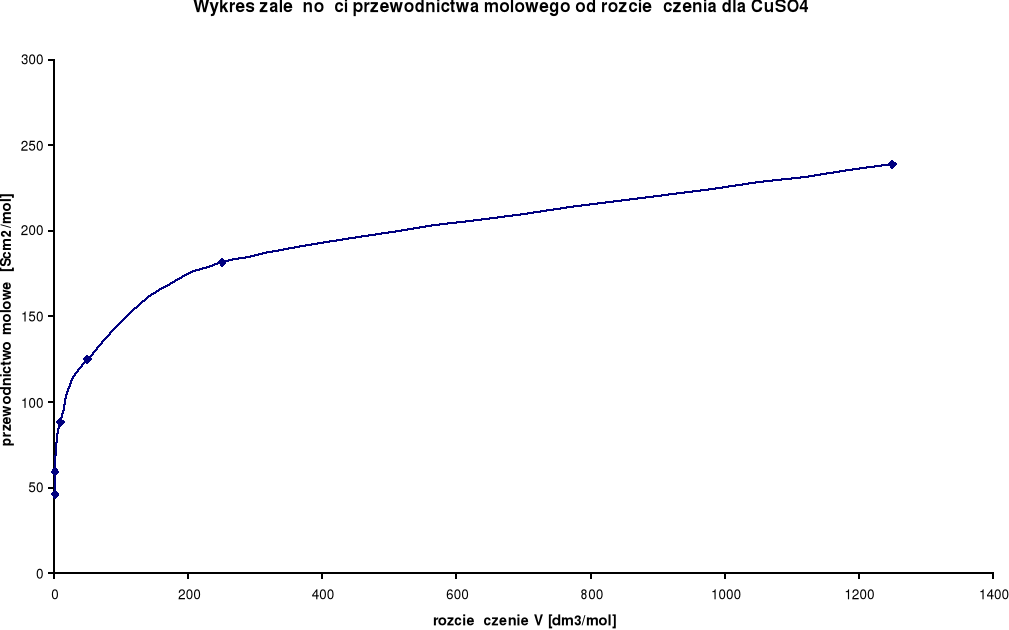
Wykresy zależności przewodnictwa molowego od rozcieńczenia:

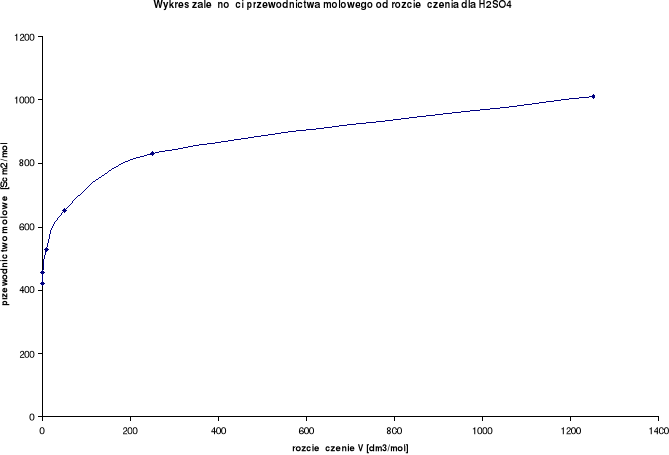
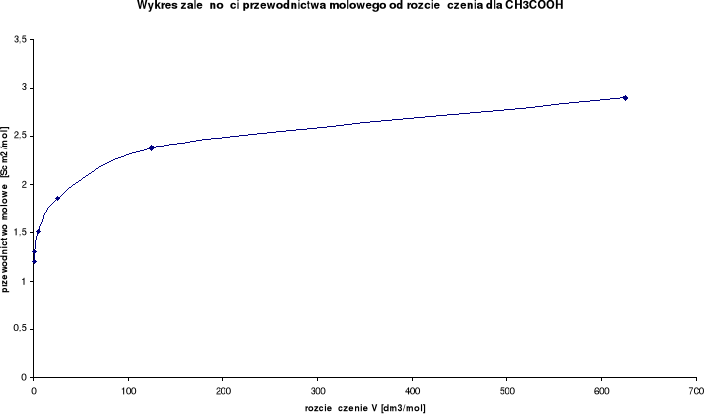
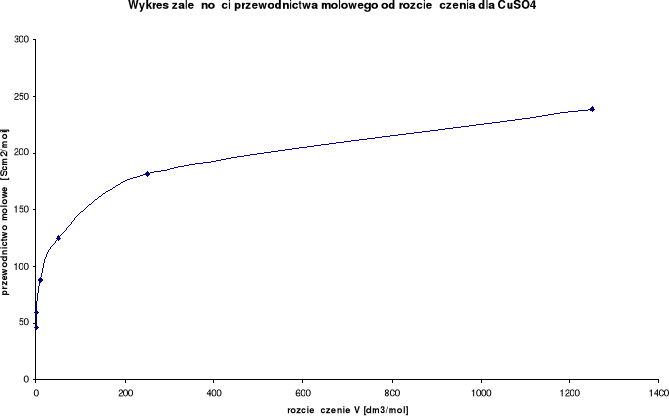
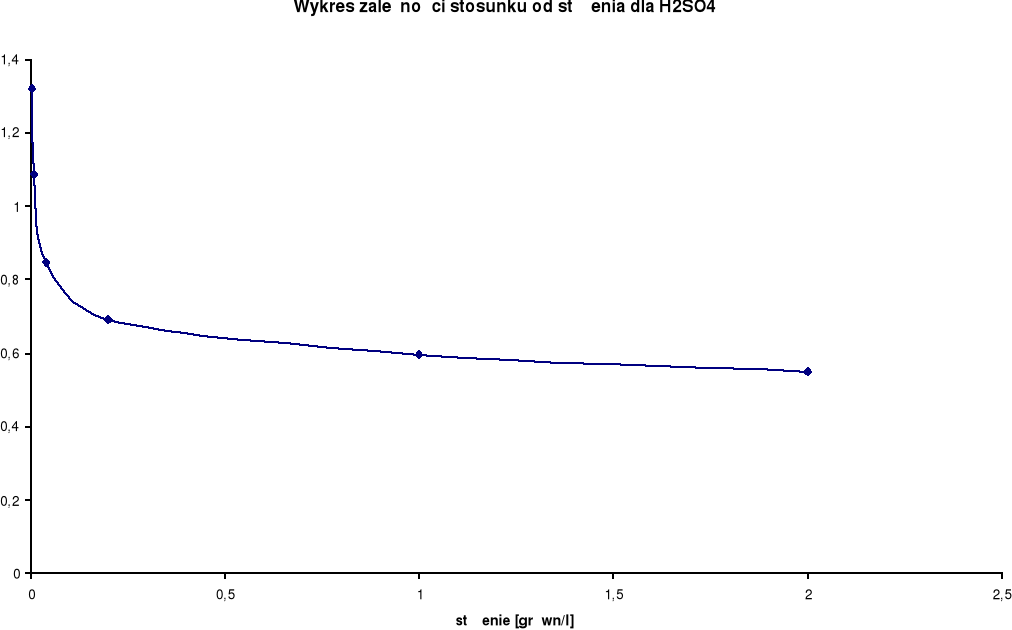
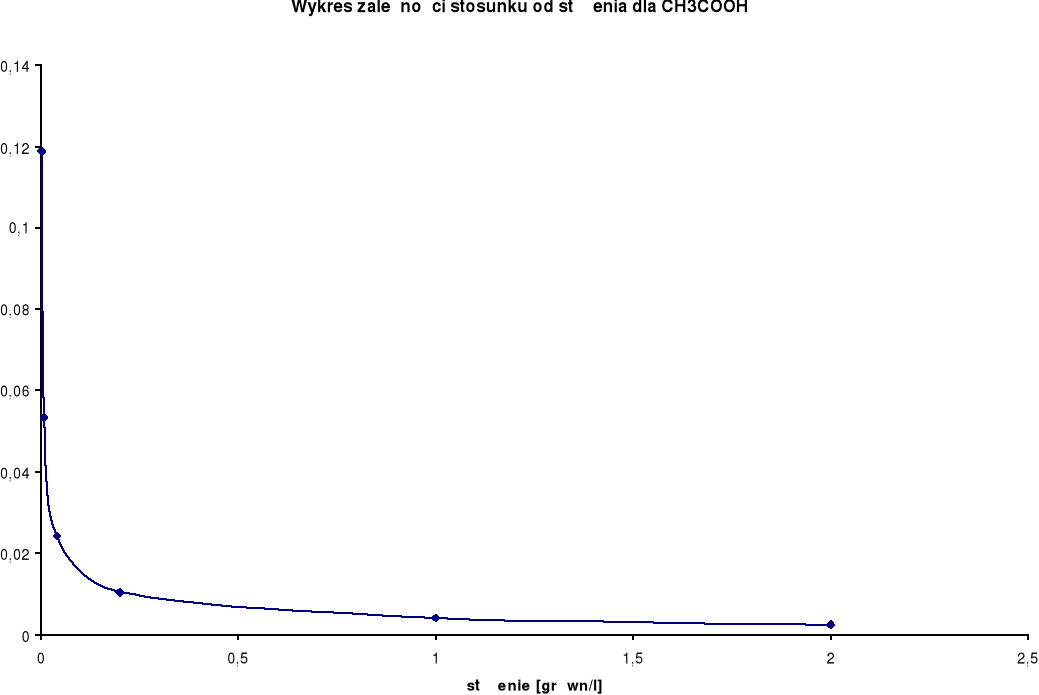
Wykresy zależności stosunku λ/λ₀ od stężenia:

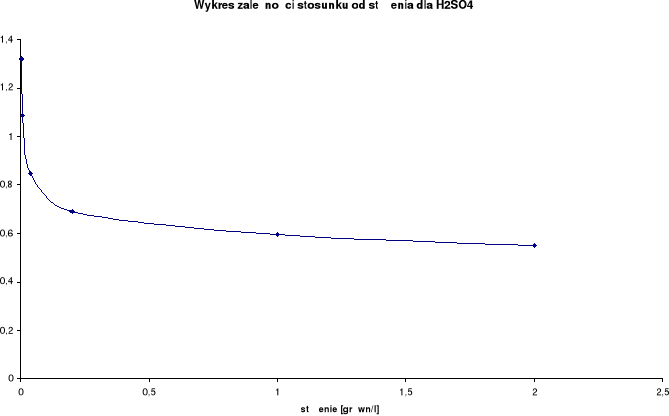
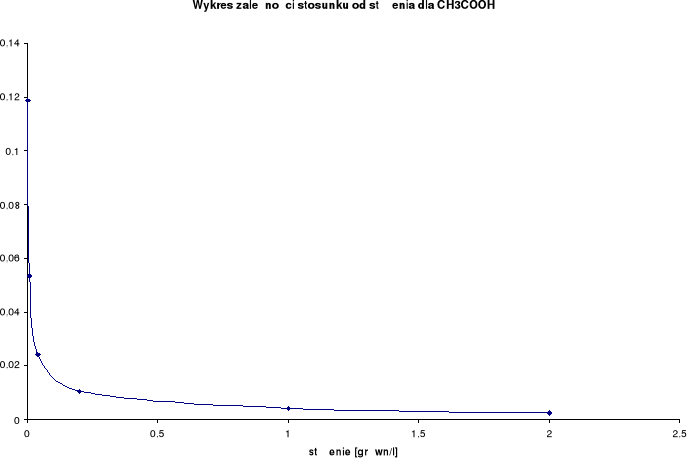
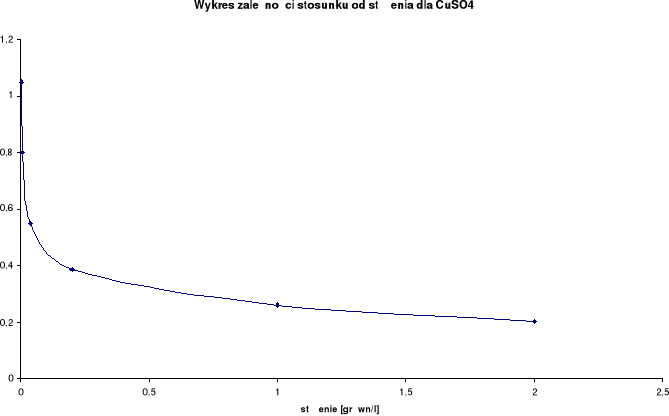
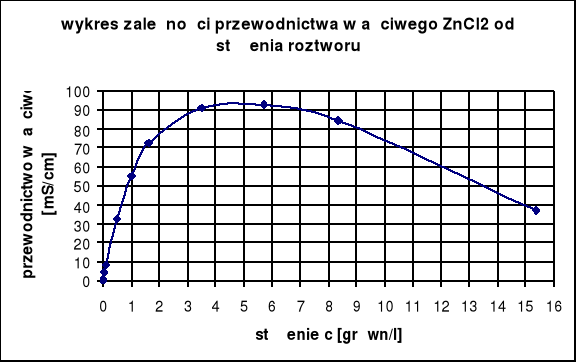
Wyznaczenie stężenia roztworu ZnCl₂:

dane: szukane:

k = 66,7 [mS/cm] c = ?

t = 21,3 [^oC]

dane tabelaryczne dla ZnCl₂:

stężenie c [grówn/l]	przewodnictwo właściwe k [mS/cm]	stężenie c [grówn/l]	przewodnictwo właściwe k [mS/cm]
0,0005	0,0508	1	55
0,001	0,107	1,606	72,7
0,005	0,508	3,493	91,2
0,01	0,98	5,72	92,6
0,05	4,35	8,353	84,5
0,1	8,2	15,37	36,9
0,5	32,5

Korzystając z tabeli odczytujemy:

c = 1 [grówn/l] → k = 55,0 [mS/cm]

c = 1,606 [grówn/l] → k = 72,7 [mS/cm]

i układamy zależność funkcji liniowej y = ax + b

55,0 = 1⋅a + b

72,7 = 1,606⋅a + b

Rozwiązując powyższy układ równań otrzymujemy:

a = 29,2; b = 25,8

zatem równanie funkcji liniowej ma postać:

y = 29,2x + 25,8

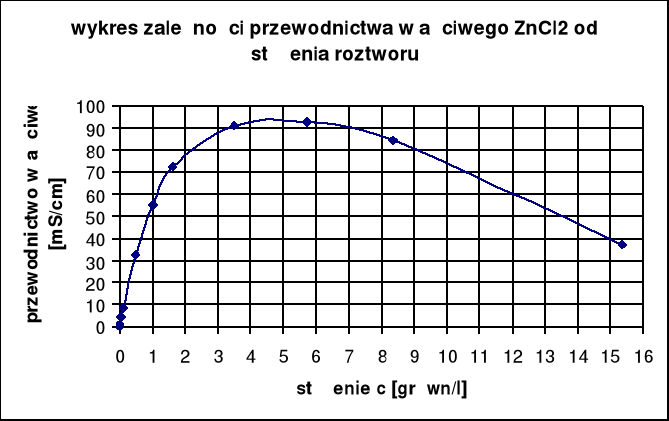
Podstawiając wyznaczone przewodnictwo właściwe k = 66,7 [mS/cm] możemy wyliczyć szukane stężenie ZnCl₂

66,7 = 29,2x + 25,8

x = 1,4

Odp: stężenie roztworu ZnCl₂ wynosi 1,4 [grówn/l]

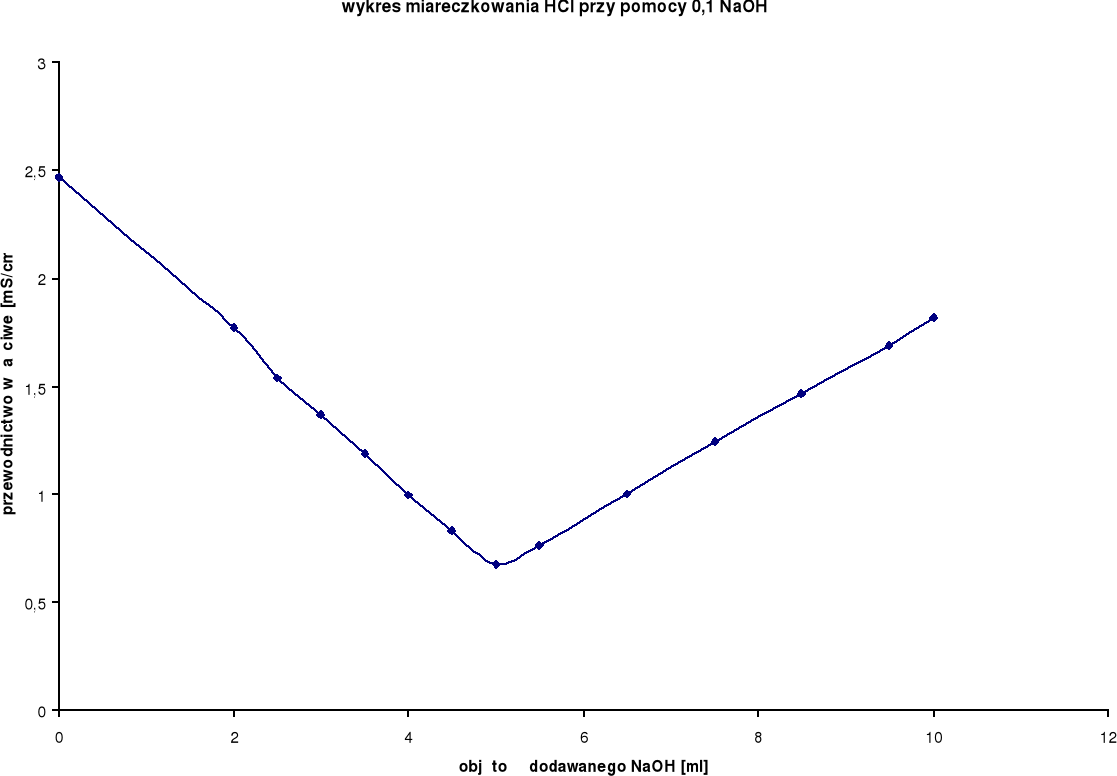
Wyniki miareczkowań konduktometrycznych dla HCl:

Rozwór miareczkowany: HCl

Rozwór miareczkujący: 0,1 n NaOH

0,1 n NaOH [ml]	przewodnictwo właściwe [mS/cm]	temperatura [^oC]	0,1 n NaOH [ml]	przewodnictwo właściwe [mS/cm]	temperatura [^oC]
0,0	2,47	21,7	5,0	0,678	21,5
2,0	1,77	21,6	5,5	0,762	21,5
2,5	1,54	21,6	6,5	1,001	21,5
3,0	1,37	21,6	7,5	1,245	21,5
3,5	1,19	21,6	8,5	1,467	21,5
4,0	0,997	21,6	9,5	1,688	21,5
4,5	0,830	21,5	10,0	1,818	21,5

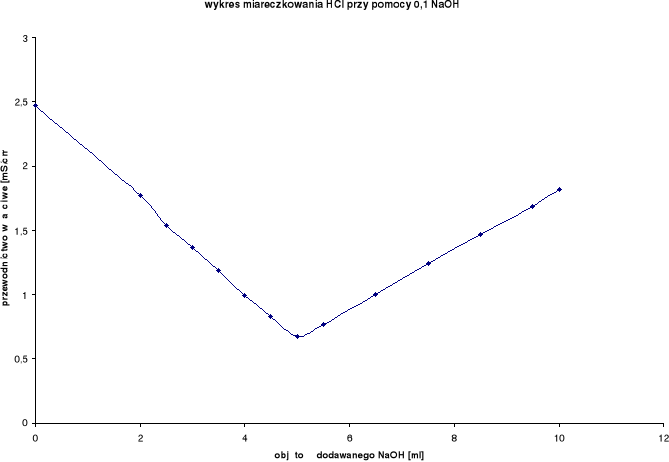
Z wykresu wynika, iż zmiareczkowanie wystąpiło po dodaniu ok. 5 ml NaOH.

Uwzględniając równanie zobojętnienie:

HCl + NaOH → NaCl + H₂O

wynika, iż do zobojętnienia 1 mola HCl potrzebny jest 1 mol NaOH. Możemy z tego wyliczyć:

5,0 ml - 0.1n (NaOH)

5,0 ml - x (HCl)

5 ⋅ x = 5 ⋅ 0,1 ⇒ x = 0,5 / 5 = 0.1 n

Odp: stężenie miareczkowanego HCl wynosiło 0.1 n.

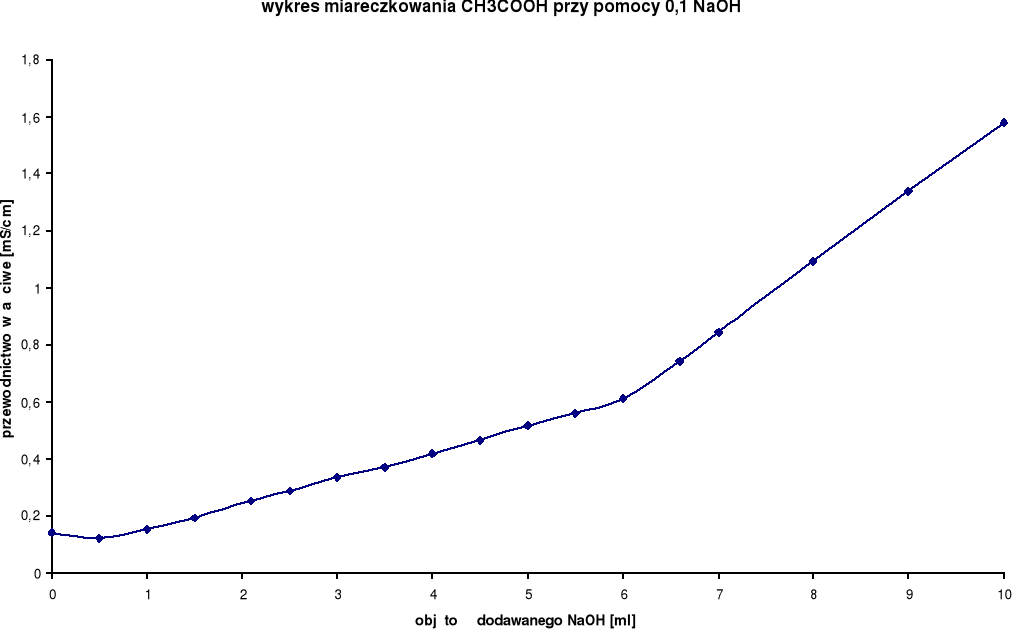
Wyniki miareczkowań konduktometrycznych dla CH₃COOH:

Rozwór miareczkowany: CH₃COOH

Rozwór miareczkujący: 0,1 n NaOH

0,1 n NaOH [ml]	przewodnictwo właściwe [mS/cm]	temperatura [^oC]	0,1 n NaOH [ml]	przewodnictwo właściwe [mS/cm]	temperatura [^oC]
0,0	0,141	21,6	4,5	0,466	21,7
0,5	0,121	21,8	5,0	0,519	21,7
1,0	0,153	21,8	5,5	0,559	21,6
1,5	0,193	21,7	6,0	0,613	21,6
2,1	0,253	21,7	6,6	0,743	21,6
2,5	0,290	21,7	7,0	0,845	21,6
3,0	0,334	21,7	8,0	1,093	21,6
3,5	0,372	21,7	9,0	1,340	21,6
4,0	0,419	21,7	10,0	1,577	21,6

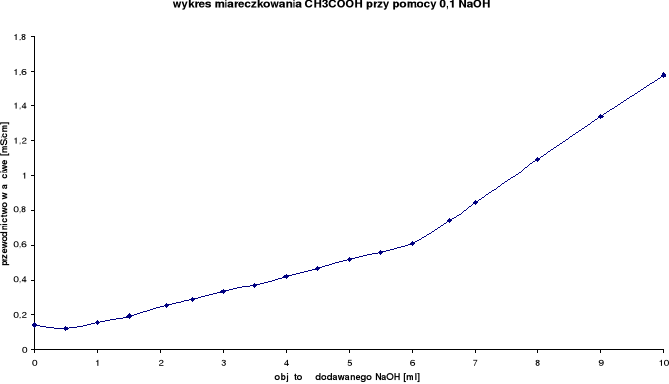
Z wykresu wynika, iż zmiareczkowanie wystąpiło po dodaniu ok. 6 ml NaOH.

Uwzględniając równanie zobojętnienie:

CH₃COOH + NaOH → CH₃COONa + H₂O

wynika, iż do zobojętnienia 1 mola HCl potrzebny jest 1 mol NaOH. Możemy z tego wyliczyć:

6,0 ml - 0.1n (NaOH)

5,0 ml - x (HCl)

6 ⋅ x = 5 ⋅ 0,1 ⇒ x = 0,5 / 6 = 0.83 n

Odp: stężenie miareczkowanego CH₃COOH wynosiło 0.83 n.

4. Wnioski:

Przewodnictwo molowe oraz stosunek λ / λ₀ wzrastają wraz ze wzrostem rozcieńczenia. Wynika to z faktu, iż wraz ze wzrostem rozcieńczenia wzrasta liczba jonów uczestniczących w przenoszeniu ładunków, a co za tym idzie wzrasta przewodnictwo molowe.

Przewodnictwo właściwe wzrasta wraz ze wzrostem stężenia.

Błąd wyznaczonej wartości stężenia ZnCl₂ może wynikać z różnicy temperatur: doświadczalnej
t = 21,3 ^oC oraz tabelarycznej t = 18 ^oC

Podczas miareczkowania mocnego kwasu solnego HCl mocną zasadą sodową NaOH na początku można zaobserwować spadek przewodnictwa właściwego, lecz po przekroczeniu granicy miarecz-kowania można zaobserwować znaczny wzrost przewodnictwa właściwego, co było spowodowane początkową wymianą „ruchliwego” kationu H⁺ na dużo wolniejszy kation Na⁺.

Podczas miareczkowania słabego kwasu octowego CH₃COOH mocną zasadą sodową NaOH można zaobserwować, po początkowym, nieznacznym zmniejszeniu przewodnictwa właściwego, spowodowanym zmniejszeniem zawartości jonów kwasu octowego, można zaobserwować wolny wzrost, spowodowany pojawieniem się szybszych jonów CH₃COONa, a po przekroczeniu granicy miareczkowania można zaobserwować, iż wzrost przewodnictwa właściwego stał się szybki, bowiem zaczęły przewodzić jony zasady sodowej.

---