Kapitalizacja złożona

K_n = K₀ (1 + r)ⁿ

K₀ =

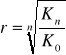
- 1

K₀ - kapitalizacja wyjściowa

r - stopa procentowa /stopa dyskontowa

n - ilość okresów

K_n - kapitalizacja po n okresach

Przykład 1.

Ile wynosi średnie roczne tempo wzrostu w latach 2000 - 2003 ?

Lata	2000	2003
koszty	300	320

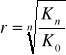
- 1

- 1

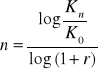
Przykład 2.

Po ilu latach kapitalizacja wyjściowa (K₀) wzrośnie trzykrotnie jeśli średnie roczne tempo wzrostu tej kapitalizacji wynosi 20% ?

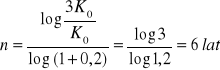
K_nm = K₀ (1 +

m - ilość podokresów w okresie

Stopa efektywna

r_ef = (1 +

Przyszła wartość renty płaconej z dołu

PWR = R

R - okresowa płatność

Przyszła wartość renty płaconej z góry

PWR = R

(1 + r)

Przykład 3.

Z końcem każdego roku pracownik wpłacał na fundusz emerytalny 5 000 zł przez okres 10 lat. Jaka będzie wartość zgromadzonych funduszy emerytalnych na koniec dziesiątego roku jeśli wpłaty te będą gromadzone na rachunku bankowym oprocentowanym 6% rocznie ?

PWR = R
= 5 000

Teraźniejsza wartość renty płatnej z dołu

TWR = R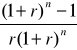

Teraźniejsza wartość renty płatnej z góry

TWR = R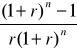

Przykład 4.

Kredyt wynosi 1 000 zł, spłata nastąpi w dwóch ratach rocznych, roczne oprocentowanie wynosi 10%.

I sposób:

Zadłużenie na początek roku	Rata kapitałowa	Odsetki	Rata spłaty	Zadłużenie na koniec roku
1	2	3	4 (2 + 3)	5 (1 - 2)
1 000	500	1 000 0,1 = 100	600	500
500	500	500 0,1 = 50	550	0
	1 000	150	1 150

Zadłużenie na koniec roku pierwszego przechodzi na początek roku następnego

II sposób:

Zadłużenie na początek roku	Rata kapitałowa	Odsetki	Rata spłaty	Zadłużenie na koniec roku
1	2 (4 - 3)	3	4	5 (1 - 2)
1 000	476,20	1 000 0,1 = 100	576,20	523,8
523,8	523,80	523,8 0,1 = 52,40	576,20	0
	1 000	152,40	1 152,40

TWR = R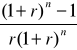

Za R podstawiam KR

K R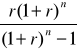
= 1 000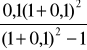
= 576,20

Teraźniejsza wartość renty wieczystej

TWR_wiecz.=

Wartość bieżąca obligacji

WBO =

ODS - odsetki

WN - wartość nominalna

Przykład 5.

Wartość nominalna obligacji wynosi 100 zł, termin wykupu obligacji - 4 lata, stopa oprocentowania obligacji wynosi 10% = stopa rynkowa. Oblicz teraźniejszą wartość obligacji.

• Jeśli nie jest podane w treści to zakładamy, że odsetki wypłacane są z dołu.

Odsetki = 100
0,1 = 10 zł - z końcem każdego roku

r = 10%

W_o=

Gdy np. r = 15%

WBO₁=

WBO₂ =

Zysk kapitałowy = 91,87 - 88,58 = 3,29

Stopa zysku kapitałowego =

Odsetki = 10 zł

Stopa bieżącego dochodu =

Stopa ogólnego dochodu =
13,29 = 10 + 3,29 (zysk kapit.)

Gdy np. stopa rynkowa = 5%

WBO₁=

WBO₁=

Stopa straty kapitałowej =

Strata kapitałowa = 113,62 - 109,30 = - 4,32

Odsetki = 10 zł

Stopa bieżącej straty kapitałowej =

Stopa ogólnej straty kapitałowej = 10 - 4,32 = 5,68

Przykład 6.

Wartość bieżąca czteroletniej obligacji wynosi 15 000 zł, a nominalna stopa oprocentowania - 11%. Oblicz nominalną wartość tej obligacji jeżeli stopa rynkowa równa się 12%.

15 000 =

15 000 = WN
0,11 + WN

15 000 = WN

WN =

Przykład 7.

Oblicz wartość rocznych odsetek od trzyletniej obligacji o wartości nominalnej 1000 zł jeśli jej cena rynkowa wynosi 1200 zł a rynkowa stopa dyskontowa równa się 20%.

1200 =

1200 = r (

1200 = r

1200 - 579 = r

621 = r

r = 0,29

Przykład 8.

Wartość nominalna obligacji wynosi 100 zł, nominalna stopa oprocentowania - 8%, okres do wykupu - 2 lata, wartość bieżąca obligacji - 105 zł. Oblicz stopę rynkową.

105 = zdyskontowane odsetki + zdyskontowana wartość nominalna

105 =

105 (1 + r)² = 8 (1 + r) + 108

105 (1 + 2r + r²) = 8 + 8r + 108

105 + 210r + 105r² = 8 + 8r + 108

105r² + 202r - 11 = 0

r₁=

r₂ =
wewnętrzna stopa zwrotu musi być +

Ryzyko

Stopa dochodu prawdopodobieństwo

A B

Głęboka recesja 4% 2% 0,1%

Łagodna recesja 6% 6% 0,2%

Stagnacja 12% 10% 0,4%

Łagodny wzrost 8% 14% 0,2%

Szybki wzrost 5% 18% 0,1%

Średnia ważona =

= 4%

dla wariantu A:

= 4 - 8,5 = - 4,5 (

)² = 20,25

6 - 8,5 = - 2,5 6,25

12 - 8,5 = 3,5 12,25

8 - 8,5 = -0,5 0,25

5 - 8,5 = -3,5 12,25

(

)²
= 20,25

6,25
0,2 = 1,25

12,25
0,4 = 4,90

0,25
0,2 = 0,05

12,25
0,1 = 1,225

9,45 = S² wariancja

S_A =

S_B = 4,4%

V_A=

V_B=

Model Gordona

P_o=
D₁ = D_o (1 + g)

g - tempo wzrostu dywidendy (stopa wzrostu dywidendy)

r - oczekiwana stopa zwrotu

D - dywidenda

Przykład 9.

Przedsiębiorstwo zamierza w końcu roku wypłacić dywidendę przypadającą na 1 akcję w kwocie 2,50 zł. Wymagana przez inwestora stopa zwrotu wynosi 12%, a stopa wzrostu dywidendy jest równa 5%. Oblicz bieżącą cenę akcji.

r = 12%, D₁ = 2,50 zł, g = 5%

P_o=
=

Jaka będzie cena P₁ po 1 roku ?

P₁=

D₂ = D₁ (1 + g)

D₂ = 2,50 (1 + 0,05) = 2,625

P₁ =

Tempo wzrostu ceny =

Tempo wzrostu dywidendy

g = stopa zysku zatrzymanego
zyskowność kapitałów własnych

stopa zysku zatrzymanego =

stopa wypłaty dywidendy =

zyskowność kapitałów własnych =

g =

Przykład 10.

Przedsiębiorstwo spodziewa się okresu szybkiego wzrostu i w związku z tym zyski i dywidendy będą rosły w tempie 15% przez następne 2 lata, 13% w trzecim roku, a w kolejnych latach to tempo ustabilizuje się na poziomie 6%. Ostatnio wypłacona dywidenda wynosiła 1,15 zł, a wymagana przez akcjonariuszy stopa dochodu z akcji wynosi 12%. Oblicz bieżącą cenę akcji tego przedsiębiorstwa.

D₁ = D_o (1 + g)

D_o = 1,15

D₁ = 1,15 (1 + 0,15) = 1,3225

D₂ = 1,3225 (1 + 0,15) = 1,5209

D₃ = 1,5209 (1 + 0,13) = 1,7186

Zdyskontowanie dywidend

= 3,62

P₃ =

D₄ = 1,7186 (1 + 0,06) = 1,8217

P₃ =

Zdyskontowanie dywidendy

P = 21,61 + 3,62 = 25,23 - cena bieżąca akcji (teoretyczna)

P_o=

r - g =

r =
stopa zwrotu

Przykład 11.

Przedsiębiorstwo wypłaca 4 zł dywidendy na 1 akcję z końcem pierwszego roku, bieżąca cena tej akcji wynosi 50 zł, a stopa wzrostu dywidendy jest równa 6%. Oblicz stopę zwrotu z tej akcji.

r =

r =

Przykład 12.

Akcje firmy X można kupić za 21,40 zł. Nabywca spodziewa się, że akcje te będą przynosiły dywidendę w pierwszym roku - 1,07 zł, w drugim - 1,1449 zł, a w trzecim roku - 1,225 zł. Nabywca spodziewa się że przy końcu trzeciego roku te akcje zostaną sprzedane za 26,22 zł. Oblicz stopę wzrostu dywidendy. Oblicz oczekiwaną dochodowość z tytułu dywidend. Jaka jest całkowita stopa dochodu w przypadku tej akcji.

D₁ = 1,07

D₂ = 1,1449

D₃ = 1,225

g₁ =

g₂ =

tempo wzrostu dywidendy wynosi 7%

stopa dywidendy =

1 rok

2 rok

3 rok

stopa dywidendy wynosi 5%Dochód z akcji ogółem wynosi (5% + 7%) 12%

Przykład 13.

W przedsiębiorstwie zasoby rudy żelaza wyczerpują się a w związku z tym sprzedaż maleje. W tym samym czasie pogłębiane są szyby górnicze a więc wzrastają koszty wydobycia. W wyniku tych zdarzeń dochody firmy i dywidendy stale się zmniejszają i spadek ten wynosi 5% rocznie. Jeżeli D_o = 5 zł a oczekiwana przez inwestorów stopa zwrotu wynosi 15% to jaka jest wartość akcji tej firmy.

D_o = 5%

g - w tym przypadku jest wartością ujemną (spadek)

D₁ = 5(1 - 0,05) = 4,75

P_o=
=

Przykład 14.

Inwestorzy wymagają 15% stopy dochodu za akcje firmy X. Jaka będzie wartość akcji tej firmy jeżeli poprzednio wypłacona dywidenda D_o =2 zł a inwestorzy spodziewają się że dywidendy te będą rosły według stałej rocznej stopy wynoszącej:

1. - 5%

2. 0% r = 0,15

3. 5% D_o = 2

4. 10%

ad. a)

D_o = 2

D₁ = 2
(0,95 = 1 - 0,05)

P_o=
=

ad. b)

P_o =

ad. c)

D₁ = 2
= 2,1 (1,05 = 1 + 0,05)

P_o=
=

ad. d)

D₁ = 2

P_o=
=

Zad. 1)

Przedsiębiorstwo lokuje w banku kwotę 1000 zł na okres 3 lat. Bank oferuje roczną stopę oprocentowania - 30%. Jaką kwotę przedsiębiorstwo będzie dysponowało po 3 latach jeśli odsetki będą kapitalizowane półrocznie.

Zad. 2)

Przy oprocentowaniu lokat bank stosuje kapitalizację miesięczną przy nominalnej stopie rocznej - 30%. Jednakże w następnym roku bank chce stosować kapitalizację półroczną. O ile należy podnieść nominalną roczną stopę procentową aby zachować tę samą atrakcyjność oprocentowania ?

Zad. 3)

Księgarnia zakupiła w wydawnictwie książki za 140 tys. zł tj. o 30% taniej w stosunku do wartości w cenach detalicznych. Jaką kwotę marży uzyskała księgarnia ?

Zad. 4)

Cena kalkulatora została najpierw zwiększona o 20% w stosunku do ceny wyjściowej a następnie obniżona o 20%. O ile procent zmieni się cena po tych operacjach w stosunku do ceny wyjściowej ?

Zad. 5)

Obligacja zapewnia stałe oprocentowanie 10% w skali roku. Nominalna wartość tej obligacji wynosi 800 zł a bieżąca wartość rynkowa 814 zł. Jaka jest roczna stopa dochodu z tej obligacji w terminie wykupu który nastąpi za 2 lata ?

---