Wstęp

Celem ćwiczenia było wyznaczenie pozornego współczynnika tarcia w czopach mechanizmu korbowego oraz wyznaczenie współczynnika tarcia suchego dla układu o 1 stopniu swobody.

Dla dowolnego przegubu mechanizmu korbowego zachodzi nierówność , gdzie

jest współczynnikiem tarcia w czopach .

Między a ( współczynnik tarcia suchego powierzchni płaskich) zachodzą następujące zależności:

W położeniu granicznym tzn. takim, przy którym zachowana jest równowaga lub, przy którym już następuje obrót, prawdziwa jest równość:

Moment tarcia wynosi :

Po przekształceniach

W ćwiczeniu korzystałem z mechanizmu korbowego przedstawionego na poniższym schemacie

Cały mechanizm korbowy był zamocowany na płycie . Korba jest połączona z korbowodem 2. Drugi koniec korbowodu jest połączony przegubowo za pośrednictwem suwaka z łącznikiem 3 wykonującym ruch posuwisto-zwrotny, przenosząc oddziaływanie sprężyny na mechanizm. Sprężyna 4 powoduje powstawanie momentu obrotowego powodującego obrót korby 1. Wychylenie graniczne, przy którym zachowana jest jeszcze równowaga mierzyłem za pomocą głębokościomierza mikrometrycznego 5.

Parametry geometryczne tego układu ( układ znajduje się w położeniu granicznym)

Wyglądają następująco:

Z zależności geometrycznych można wyprowadzić wzór : ,

z którego obliczałem współczynnik tarcia w czopach.

Do wyznaczenia współczynnika tarcia suchego dla układu o jednym stopniu swobody wykorzystałem wykres- rozwiązanie układu równań:

Obliczenia

Lp.	Pomiar w położeniu „0” [mm]	Pomiar przy odskoku [mm]	Wychylenie X [mm]	σ'xi=xi-xśr	(σ'xi)^2
1	46,20	39,20	7,00	-1,08	1,1664
2	46,20	38,35	7,85	-0,23	0,0529
3	46,20	39,85	6,35	-1,73	2,9929
4	46,20	36,20	10,00	1,92	3,6864
5	46,20	38,40	7,80	-0,28	0,0784
6	46,20	37,30	8,90	0,82	0,6724
7	46,20	39,45	6,75	-1,33	1,7689
8	46,20	37,30	8,90	0,82	0,6724
9	46,20	38,00	8,20	0,12	0,0144
10	46,20	37,15	9,05	0,97	0,9409

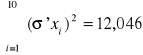
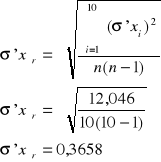
Z rozkładu t - Studenta na poziomie ufności  = 0.05

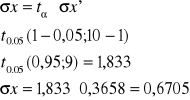
wychylenie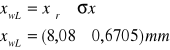

L=500 mm R=100 mm

Analiza błędów metodą różniczki zupełnej

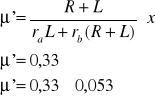
Wyznaczanie współczynnika tarcia suchego dla układu o jednym stopniu swobody

Do komputera wprowadzono następujące dane :

tłumienie tarciem tłumienie tarciem

wiskotycznym suchym

masa drgająca 1 kg 1 kg

współ. tłumienia 7,5 60

przemieszczenie 1 m 1 m

prędkość początkowa -5 m/s -5 m/s

liczba okresów 15 15

współczynnik sprężystości 1 N/m 1 N/m

Współczynnik tarcia suchego oblicza się ze wzoru :

Korzystając z wykresu określiłem amplitudy: x₀ = 4,10, x_n+2 = 2,47

 = 0.25(4,10 - 2,47)1 / 1∗10 =0,38

Wnioski

1. Wyznaczony współczynnik tarcia mieści się w granicach teoretycznych (0.23-0.34), zatem został obliczony poprawnie

2. O własnościach ruchu tłumionego tarciem suchym można powiedzieć, że:

- obwiednią drgań jest linia prosta

- kolejne amplitudy zmieniają się wg postępu arytmetycznego

- przemieszczenie ma skończoną liczbę miejsc zerowych

- okres drgań jest stały i równy okresowi drgań swobodnych bez tarcia

- ruch ustaje po skończonej liczbie wahnięć

- ponieważ przy małych wychyleniach siła jest mniejsza od siły tarcia, to ruch ustaje nie w miejscu zerowym

3. Różnice w wyglądzie trajektorii ruchu ciała tłumionego tarciem suchym i lepkim określają rozwiązania równań różniczkowych:

dla tłumienia tarciem suchym

dla tłumienia tarciem lepkim

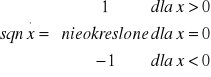
4. Dla trajektorii ruchu ciała tłumionego tarciem lepkim wiskotycznym obwiednią jest krzywa wykładnicza (odmiennie niż dla trajektorii ruchu ciała tłumionego tarciem suchym). Liczba miejsc zerowych zależy od warunków początkowych, okres drgań jest stały i wyraża się wzorem:

2

---