Wykład 2

Kinematyka ciała sztywnego (CS)

2.1 Ruch ciała sztywnego swobodnego

Ciało sztywne - zbiór punktów, między którymi wzajemne odległości są stałe.

Ruch ciała sztywnego w przestrzeni E³ jest jednocześnie opisany za pomocą trzech punktów sztywno związanych z tym ciałem i nie leżących na jednej prostej.

Dla trzech punktów: A(x_A, y_A, z_A), B(x_B, y_B, z_B), C(x_C, y_C, z_C) mamy równania wektorowe ruchu:
,
,

Liczba stopni swobody ciała sztywnego:

Zauważmy, że dla ciała sztywnego odległości między punktami A, B, C są stałe:

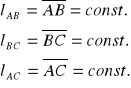
Stąd mamy trzy równania więzów:

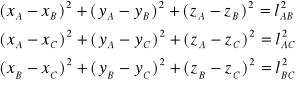
Liczba stopni swobody ciała sztywnego - liczba niezależnych współrzędnych określających położenie tego ciała. W przestrzenie E³ ciało sztywne w ruchu dowolnym posiada: k = 9 - 3 = 6 stopni swobody. Po nałożeniu na ciało sztywne pewnych ograniczeń w ruchu (więzów) zmniejszamy liczbę stopni swobody, np.: w ruchu obrotowym wokół stałej osi ciało sztywne ma 1 stopień swobody (kąt obrotu wokół tej osi).

Prędkości dwóch dowolnych punktów ciała sztywnego:

Obieramy punkty A i B ciała sztywnego i prowadzimy przez nich prostą. Zakładamy, że punkty A i B mają prędkości
i
, które tworzą z tą prostą kąty odpowiednio α i β. Wtedy:

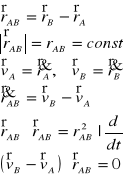
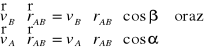
Twierdzenie o prędkościach dwóch dowolnych punktów ciała sztywnego:

Rzuty wektorów prędkości dwóch dowolnych punktów ciała sztywnego na prostą łączącą te punkty są sobie równe.

Klasyfikacja ruchów ciała sztywnego:

Ogólnym przypadkiem ruchu ciała sztywnego jest ruch dowolny (swobodny) względem nieruchomego układu Oxyz.

1. Ruch dowolny ciała sztywnego, k=6.

2. Ruch postępowy ciała sztywnego, k=3.

3. Ruch obrotowy ciała sztywnego wokół własnej osi, k=1.

4. Ruch płaski ciała sztywnego, k=3.

5. Ruch kulisty ciała sztywnego, k=3.

2.2 Ruch dowolny ciała sztywnego:

Do opisu tego ruchu wprowadzimy dwa układy odniesienia:

- Oxyz - układ stały (nieruchomy).

- O₁x₁y₁z₁ - układ ruchomy względem Oxyz.

Z układem O₁x₁y₁z₁ jest związane pewne ciało sztywne C₁.

Interpretacja geometryczna ruchu dowolnego:

Ruch punktu A
C₁ ruch bieguna O₁ + ruch wokół bieguna O₁.

- wektor wodzący punktu A w układzie Oxyz.

- wektor wodzący punktu A w układzie O₁x₁y₁z₁.

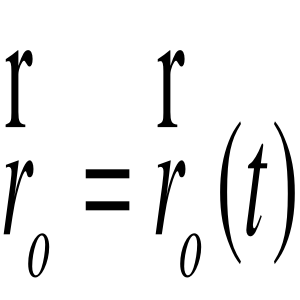
- wektor wodzący bieguna O₁ w układzie Oxyz.

Chwilowy ruch obrotowy ciała C₁ (Ruch wokół bieguna O₁):

- wektor małego obrotu [rad] względem chwilowej osi obrotu l.

Wektor chwilowej prędkości kątowej ciała C₁:

[rad/s]

- wektor zmieniający swój kierunek, lecz zawsze leżący na chwilowej osi obrotu.

Prędkość punktu A ciała w jego chwilowym ruchu obrotowym:

Torem punktu A jest łuk okręgu o promieniu h.

h=rთsina

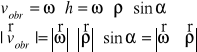
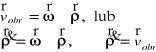
- wektor prędkości punktu A ciała sztywnego w chwilowym ruchu obrotowym.

Prędkość dowolnego punktu A:

,

,

Przyspieszenie dowolnego punktu A:

Przyspieszenie punktu A ciała sztywnego względem Oxyz:

Podstawiamy: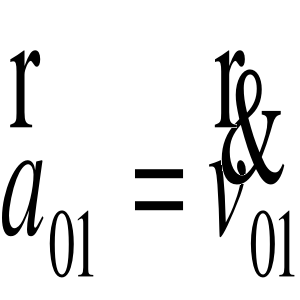
,
,
,

- wektor przyspieszenia kątowego, [rad/s²]

- przyspieszenie bieguna O₁ względem Oxyz.

- przyspieszenie obrotowe.

- przyspieszenie doosiowe (dośrodkowe)

natomiast

2.3 Ruch postępowy ciała sztywnego:

Ruch postępowy ciała sztywnego - występuje wtedy, kiedy prosta łącząca dwa dowolne punkty tego ciała przemieszcza się równolegle względem swego położenia początkowego w czasie ruchu.

AB||A1B1 ρ=const

r_B = r_A + ρ

Po zróżniczkowaniu:

W ruchu postępowym wszystkie punkty ciała sztywnego mają takie same wektory prędkości i przyspieszenia i poruszają się po torach przystających.

Wnioski

:

- Ruch postępowy ciała sztywnego jest określony, jeżeli znamy ruch dowolnego punktu tego ciała.

Równania ruchu dowolnego punktu A ciała:
,
,

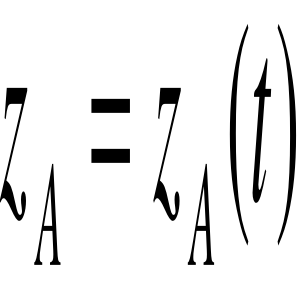
- Ciało sztywne w ruchu postępowym na 3 stopnie swobody.

2.4 Ruch obrotowy ciała sztywnego względem stałej osi:

Ruch obrotowy ciała sztywnego - występuje wtedy, kiedy jedna prosta związana z tym ciałem jest nieruchoma.

Każdy punkt ciała sztywnego w ruchu obrotowym porusza się po okręgu, którego płaszczyzna jest prostopadła do osi obrotu.

Liczba stopni swobody: k=3-2=1

Prędkość i przyspieszenie kątowe w ruchu obrotowym:

Wektor prędkości kątowej:

,

Wektor przyspieszenia kątowego:

,

Wartości prędkości i przyspieszenia:

,

Prędkość i przyspieszenie dowolnego punktu A (patrz wykład 3):

Wektor prędkości dowolnego punktu A:

Wartość (moduł) wektora prędkości dowolnego punktu A:

Wektor przyspieszenia dowolnego punktu A:

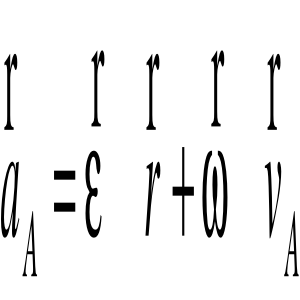
Wprowadzamy oznaczenia:

,
przyspieszenie styczne

,
przyspieszenie normalne (dośrodkowe)

Wartość (moduł) wektora przyspieszenia punktu A:

Przyspieszenie styczne i dośrodkowe dowolnego punktu A:

- Wniosek:
nie zależy od wyboru punktu A.

Ruch obrotowy jednostajny i jednostajnie zmienny ciała sztywnego:

1. Ruch obrotowy jednostajny:

Równanie ruchu jednostajnego

2. Ruch obrotowy jednostajnie zmienny:

Równania ruchu jednostajnie zmiennego:
,

2.5 Ruch płaski ciała sztywnego:

Ruch płaski ciała sztywnego - ruch, w którym wszystkie punkty tego ciała poruszają się w nieruchomych płaszczyznach równoległych do pewnej płaszczyzny π₀ - zwanej płaszczyzną kierującą.

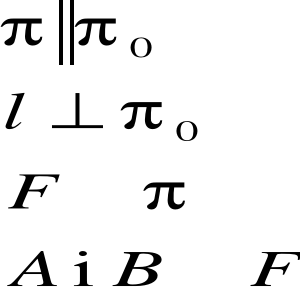
F - figura płaska będąca przekrojem ciała sztywnego płaszczyzną
.

Zauważmy, że w ruchu płaskim wszystkie punkty ciała sztywnego leżące na prostej l mają jednakowe prędkości i przyspieszenia oraz poruszają się po identycznych torach.

Wniosek: Ruch płaski ciała sztywnego można zastąpić ruchem figury płaskiej F, pozostającej w czasie ruchu na płaszczyźnie
.

Do opisu położenia tej figury wystarczy wybrać dwa dowolne punkty A(x_A, y_A) i B(x_B, y_B) a więc 4 współrzędne kartezjańskie.

---