Podciąg
Materiał.
BETON B-25 STAL AIII
Zestawienie obciążeń.
Obciążenie stałe powierzchniowe.
Materiał |
grubość |
γ(n) |
qk |
γf |
g0 |
|
[cm] |
[kN/m3] |
[kN/m2] |
- |
[kN/m2] |
Lastrico |
3 |
22 |
0,66 |
1,2 |
0,792 |
Płyta żelbetowa |
9 |
24 |
2,16 |
1,1 |
2,376 |
Tynk cem.-wap. |
1,5 |
21 |
0,315 |
1,3 |
0,410 |
|
|
|
Σ=3,135 |
|
Σ=3,578 |
Obciążenie stałe.
Element |
wymiary |
γ(n) |
qk |
γf |
g0 |
|
[cm] |
[kN/m3] |
[kN/m] |
- |
[kN/m] |
Żebro |
20×40 |
24 |
1,92 |
1,1 |
2,11 |
Podciąg |
25×75 |
24 |
5,04 |
1,1 |
5,54 |
Obciążenie zmienne.
pk=10,5[kN/m2] γf=1,2 p0=12,6[kN/m2]
Obciążenie siłami skupionymi.

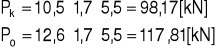
Długotrwała część obciążenia zmiennego:
![]()
Schemat statyczny.
Obliczenie sił wewnętrznych.
|
MA |
M1 |
M2 |
M3 |
MB |
M4 |
M5 |
M6 |
MC |
TA |
TBl |
TBp |
TCl |
|
0 |
2,057 |
2,516 |
1,275 |
-1,666 |
-1,139 |
-0,611 |
-0,083 |
0,444 |
1,270 |
-1,730 |
0,310 |
0,310 |
|
0 |
-0,304 |
-0,622 |
-0,941 |
-1,260 |
1,264 |
2,088 |
1,212 |
-1,364 |
-0,187 |
-0,187 |
1,485 |
-1,515 |
|
0 |
0,083 |
0,170 |
0,256 |
0,343 |
-0,084 |
-0,511 |
-0,938 |
-1,364 |
0,051 |
0,051 |
-0,251 |
-0,251 |
|
0 |
-0,027 |
-0,055 |
-0,083 |
-0,112 |
0,027 |
0,166 |
0,305 |
0,444 |
-0,017 |
-0,017 |
0,082 |
0,082 |
Mmax |
0 |
350,69 |
406,30 |
207,99 |
-106,44 |
155,80 |
327,23 |
205,74 |
4,35 |
|
|
|
|
Mmin |
0 |
59,59 |
29,71 |
-93,01 |
-504,76 |
-140,38 |
-70,50 |
-93,26 |
-421,65 |
|
|
|
|
Msdk |
0 |
192,68 |
229,17 |
99,71 |
|
|
165,48 |
|
|
|
|
|
|
Tmax |
|
|
|
|
|
|
|
|
|
216,82 |
-96,61 |
309,74 |
-28,69 |
Tmin |
|
|
|
|
|
|
|
|
|
37,16 |
-330,46 |
59,04 |
-282,93 |
RA |
|
|
|
|
|
|
|
|
|
206,97 |
|
|
|
RB |
|
|
|
|
|
|
|
|
|
|
644,71 |
|
|
RC |
|
|
|
|
|
|
|
|
|
|
|
|
565,44 |
Geometria przekroju.
Wymiary podciągu wynoszą 0,25×0,75 m. Wysokość użyteczna przekroju w licu podpory wynosi (otulina 0,029):
![]()
Wysokość użyteczna przekroju w przęśle (pręty ∅22, otulina 0,02, pręty w płycie ∅8, pręty w żebrze ∅18):
![]()
Szerokość współpracująca płyty (ze względu na występowanie sił skupionych redukcja o 20%):
przęsło skrajne
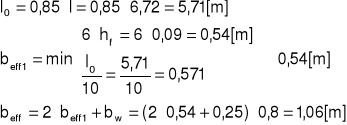
przęsło środkowe
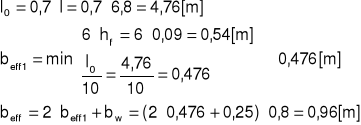
Zbrojenie na zginanie.
Momenty przęsłowe:
M2=406,3[kNm]
![]()
![]()
- przekrój pozornie teowy
![]()
Przyjęto 5×∅22, AS=19,01[cm2], ρ=0,918%
M5=327,23[kNm]
![]()
![]()
Przyjęto 4×∅22, AS=15,2[cm2], ρ=0,811%
Momenty podporowe:
Moment w osi podpory: MB=-504,76[kNm]. Moment w licu podpory wynosi:
![]()
![]()
![]()
![]()
Przyjęto 3×∅32, AS=24,13[cm2], ρ=1,29%
Moment w osi podpory: MC=-421,65[kNm]. Moment w licu podpory wynosi:
![]()
![]()
![]()
![]()
Przyjęto 3×∅32, AS=24,13[cm2], ρ=1,29%
Zbrojenie na ścinanie.
Podpory skrajne A, E
VSd=TA=216,82[kN]
Przyjmuje się, że do podpory zostaną doprowadzone dołem 3×∅22 o AS=11,40[cm2].
![]()
![]()
(przyjęto1,0)
![]()
![]()
konieczne zbrojenie na ścinanie.
![]()
![]()
Odcinek ltA-1 sięga do siły skupionej w odległości 1,615[m], podzielono go na dwa równe odcinki zbrojone samymi strzemionami ∅8.
![]()
VSd=216,82[kN]
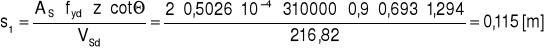
Przyjęto rozstaw 11[cm]. Zastosowano takie samo zbrojenie na drugiej części odcinka ltA-1.
Podpory pośrednie B, D
VSd=TBl=330,46[kN]
Przyjmuje się, że do podpory zostaną doprowadzone dołem 3×∅22 o AS=11,40[cm2].
![]()
konieczne zbrojenie na ścinanie.
Odcinek ltB-3 sięga do siły skupionej w odległości 1,7[m], podzielono go na dwa równe odcinki zbrojone samymi strzemionami ∅8.
![]()
VSd=330,46[kN]
![]()
Przyjęto rozstaw 8[cm]. Zastosowano takie samo zbrojenie na drugiej części odcinka ltB-3.
![]()
- konieczne zbrojenie na ścinanie
![]()
Zbrojenie na odcinku 3-2
VSd=T3p=158,15[kN]
Odcinek lt3-2 sięga do siły skupionej w odległości 1,7[m], podzielono go na dwa równe odcinki zbrojone samymi strzemionami ∅8.
![]()
VSd=158,15[kN]
![]()
Przyjęto rozstaw 16[cm]. Zastosowano takie samo zbrojenie na drugiej części odcinka lt3-2.
Z uwagi na podobną wartość siły tnącej z prawej strony podpory B i z lewej strony podpory D zastosowano symetryczne zbrojenie.
Podpora C
VSd=TCl=282,93[kN]
Przyjmuje się, że do podpory zostaną doprowadzone dołem 3×∅22 o AS=11,40[cm2].
![]()
![]()
(przyjęto1,0)
![]()
![]()
konieczne zbrojenie na ścinanie.
![]()
Odcinek ltC-6 sięga do siły skupionej w odległości 1,7[m], podzielono go na dwa równe odcinki zbrojone samymi strzemionami ∅8.
![]()
VSd=282,93[kN]
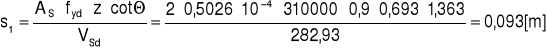
Przyjęto rozstaw 9[cm]. Zastosowano takie samo zbrojenie na drugiej części odcinka ltC-6.
![]()
- konieczne zbrojenie na ścinanie
![]()
Zbrojenie na odcinku 6-5
VSd=T5p=110,625[kN]
Odcinek lt6-5 sięga do siły skupionej w odległości 1,7[m], podzielono go na dwa równe odcinki zbrojone samymi strzemionami ∅8.
![]()
VSd=158,15[kN]
![]()
Przyjęto rozstaw 23[cm]. Zastosowano takie samo zbrojenie na drugiej części odcinka lt6-5.
Z uwagi na identyczną wartość siły tnącej z prawej strony podpory C zastosowano symetryczne zbrojenie.
Minimalny stopień zbrojenia na ścinanie.
![]()
Zbrojenie strefy przekazania siły skupionej na podciąg.
Maksymalna reakcja z żebra: Rmax=117,81+54,49=172,30[kN]
![]()
Zastosowano 4 strzemiona (po dwa z każdej strony) w odległości 20mm i 70mm od lica żebra.
Stan graniczny ugięcia.
Msdk=229,17[kNm]
Przyjęto wiek betonu w chwili pełnego obciążenia 90 dni.
![]()
RH=50%
Końcowy współczynnik pełzania ![]()
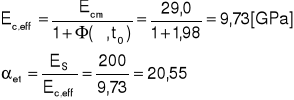
Przekrój pozornie teowy, zbrojenie 5∅22 o As=19,04[cm2].
![]()
charakterystyka przekroju niezarysowanego - położenie osi obojętnej.

Moment bezwładności.

Wskaźnik zginania
![]()
Moment rysujący
![]()
Przekrój pracuje jako zarysowany
charakterystyka przekroju zarysowanego
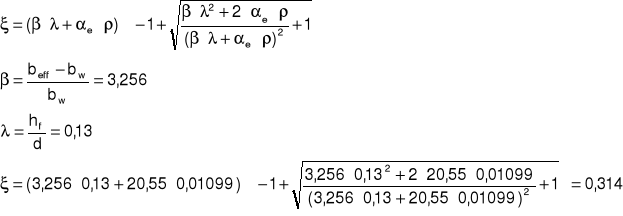
Moment bezwładności
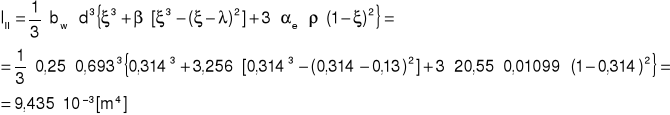
Sztywność przekroju

Ugięcie belki
![]()
Ugięcia nie zostały przekroczone.
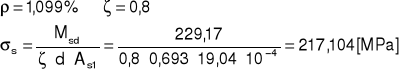
Nie oblicza się szerokości rozwarcia rys ze względu na warunek normowy:
Szerokość rozwarcia rys można uważać za ograniczoną do 0,3[mm] jeśli maksymalna średnica prętów (20mm) jest mniejsza niż 32mm (wartość maksymalna przy danym ρ i σs).
Długość zakotwienia.
Zakotwienie zbrojenia dolnego:
Podstawowa długość zakotwienia
![]()
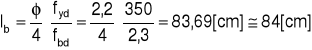
Wymagana długość zakotwienia
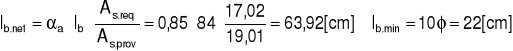
Długość zakotwienia prętów zbrojenia rozciąganego elementu zamocowanego w murze
![]()
Przedłużenie pręta poza krawędź podpory
![]()
![]()
Zakotwienie zbrojenia górnego:
Podstawowa długość zakotwienia
![]()
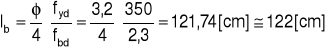
Wymagana długość zakotwienia
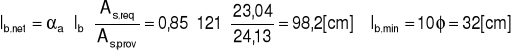
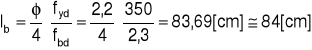
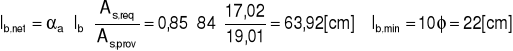
![]()
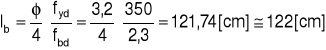
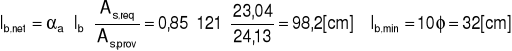
Wyszukiwarka
Podobne podstrony:
Kierowanie procesem inwestycyjnym, Budownictwo bez segregacji
Budownictwo wodne kolokwium 2, Budownictwo bez segregacji
BETONY , Budownictwo bez segregacji
elektryka, Kierunki studiów, Architektura, Materiały do nauki=), Budownictwo, Segregacja tematyczna,
!DRUK! Sciaga (beta) bez krzyzykow, Budownictwo, beton, zaliczenie
elektryka, Kierunki studiów, Architektura, Materiały do nauki=), Budownictwo, Segregacja tematyczna,
BUDOWNICZY NOWEGO ŚWIATA BEZ BOGA I
Segregacja śmieci
Segregacja poszkodowanych
bez makijazu www prezentacje org
Budown stropy
BUDOWNICTWO OGÓLNE WYKŁAD10S4
miesnie szkieletowe glowy, szyji, brzucha i grzbietu bez ilustr
Bez tytułu 1
1 Budownictwo ogólne sem IV
więcej podobnych podstron