SPRAWOZDANIE Z LABORATORIUM MECHANIKI PŁYNÓW

Temat 16: Przepływ w przedowach wentylacyjnych

Skład zespołu:

Magdalena Kozak

Marzena Daśko

Radosław Kalinowski

Sergiusz Goławski

1.Wprowadzenie

Gaz rzeczywisty ma podobne właściwości jak ciecz, a więc przy przepływie przez np.: zwężki, przewody wentylacyjne, kolanka itp. napotyka na opory tarcia. Opory te są pokonywane kosztem energii kinetycznej, która jest zamieniana na ciepło lub drgania.

Do pomiaru strugi powietrza w przewodzie wentylacyjnym zastosowany został pierścień Recknagla, który zainstalowano w części przewodu o kołowym poprzecznym przekroju. Jest zbudowany z zespołu rurek Pitote`a usytuowanych osiowo-symetrycznie w ten sposób, że ciśnienie dynamiczne mierzone jest w takiej odległości od środka przewodu, w której prędkość jest równa prędkości średniej. Przy średnicy przewodu D=200 mm odległość ta wynosi y=22,3 mm.

Średnia prędkość w przewodzie:

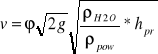
(na potrzeby ćwiczenia
=1) (1.1)

Objętościowe natężenie przepływu:

(1.2)

gdzie: A_o - pole powierzchni poprzecznego przekroju przewodu

Do wyznaczenia zależności λ = λ (Re) służy prosty odcinek przewodu. Opory liniowe (współczynnik λ) w przewodach wentylacyjnych oblicza się na podstawie wzoru Darcy - Weisbacha, którego ostateczna postać po przekształceniach jest następująca :

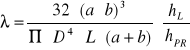
(1.3)

gdzie : h_L - wysokość dynamicznego ciśnienia mierzonego pierścieniem Recknagla [m _H2O]

h_PR - wysokość dynamicznego ciśnienia mierzonego na odcinku prostym [m _H2O]

Liczbę Reynoldsa (Re) wyznaczamy ze wzoru :

(1.4)

Dla
- kinematyczny współczynnik lepkości

Wartość współczynnika oporów liniowych ζ określa się za pomocą wzoru na całkowite opory hydrauliczne :

h_C = h_L + h_M

gdzie : h_C - opory całkowite

h_l - opory liniowe

h_m - opory miejscowe

Wzór na współczynnik oporów miejscowych :

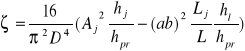
(1.5)

gdzie : D_r - średnica równoważna przewodu

A_j- pole przekroju poprzecznego rozpatrywanego odcinka, na którym występują straty miejscowe

h_j - łączne straty wysokości ciśnienia na odcinku o długości L_x

Współczynnik chropowatości natomiast wyznaczany będzie ze wzoru Prandtla-Nikuradsego:

(1.8)

Gdzie: D- średnica równoważna przewodu

Po przekształceniu wzoru:

2. Warunki laboratoryjne.

- średnica pierścienia Recknagla D=200mm=0.2m

- temperatura otoczenia t=22^oC

stąd:

- gęstość cieczy manometrycznej
_cm= 997,77 kg/m³

- gęstość powietrza
^'=
= 1.17 kg/m³

- kinematyczny współczynnik lepkość
=15.06*10^-6 m²/s

- współczynnik prędkości
= 1

- przyspieszenie ziemskie g= 9.81 m²/s

- wymiary przewodu a= 0.2004 m b=0.15m

- średnica równoważna przewodu D_r= 171,575 mm=0,1716m

- długość prostego odcinka przewodu L= 9.15 m

- długość łuku segmentowego L_x= 6,47 m

- długość łuku L_x= 6,35 m

Ciecz manometryczna WODA.

3. Wyniki doświadczenia

Tabela 1. Odczyty mikromanometrów MK - 1 dla poszczególnych elementów układu

Lp.	Pierscień Recknagla h7		Łuk h8		Łuk segmentowy h6		Prosty odcinek przewodu hL
	h8 [mm]	h8śr [m]	h8 [mm]	h8śr [m]	h6 [mm]	h6śr [m]	hL [mm]	hLśr [m]
1	4,75	0,00475	3,40	0,003395	3,50	0,0035	4,80	0,004795
			4,75				3,39			3,50		4,79
	2		4,10		0,004075		3,05		0,003045	3,04	0,003035	4,30	0,00429
			4,05				3,04			3,03		4,28
	3		3,70		0,00369		2,90		0,002895	2,70	0,002695	3,90	0,003895
			3,68				2,89			2,69		3,89
	4		3,25		0,003245		2,57		0,002565	2,35	0,002345	3,45	0,003445
			3,24				2,56			2,34		3,44
	5		2,25		0,002245		2,05		0,002045	1,70	0,00169	2,55	0,002545
			2,24				2,04			1,68		2,54
	6		2,20		0,00219		1,75		0,00174	1,50	0,00149	2,25	0,002245
			2,18				1,73			1,48		2,24
	7		1,30		0,001295		1,50		0,00149	1,05	0,00104	1,65	0,00164
			1,29				1,48			1,03		1,63
	8		0,65		0,00064		1,05		0,00104	0,26	0,00026	0,95	0,00094
			0,63				1,03			0,26		0,93
	9		0,03		0,00003		0,70		0,000695	0,04	0,00004	0,40	0,00039
			0,03				0,69			0,04		0,38
	10		0,01		0,00001		0,40		0,000395	0,01	0,00001	0,01	0,00001
			0,01				0,39			0,01		0,01

4. Obliczenia wielkości fizycznych.

1. Wyznaczenie objętościowego natężenia przepływu Q oraz zależności
   :
   

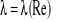
Schemat i wyniki wyliczeń przedstawiono dla pierwszej serii pomiarowej.

Pozostałe wykonane analogicznie i zestawione zostały w tabeli 2 .

Prędkość strumienia w przewodzie kołowym:

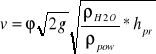
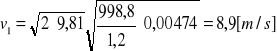
Pole przekroju przewodu kołowego Ao :

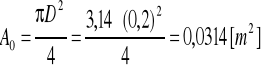
Natężenie strumienia powietrza

Pole przekroju przewodu prostokątnego Ap:

Prędkość w przewodzie prostokątnym Vp[m/s]:

Liczba Reynoldsa:

Współczynnik strat liniowych:

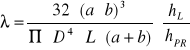
Tabela 2.

Lp.	Predkość w przewodzie kołowym Vo [m/s]	Q[m^3/s]	Prędkość w przewodzie prostokątnym Vp [m/2]	Re
1						8,900	0,2795	9,2971	105919,492	0,01738
						2	8,252	0,2591	8,6203	98208,828	0,01809
						3	7,853	0,2466	8,2030	93454,432	0,01814
						4	7,364	0,2312	7,6925	87638,325	0,01824
						5	6,125	0,1923	6,3983	72894,522	0,01948
						6	6,050	0,1900	6,3195	71996,068	0,01762
						7	4,652	0,1461	4,8595	55363,253	0,02176
						8	3,270	0,1027	3,4162	38920,347	0,02524
						9	1,961	0,0616	2,0480	23331,929	0,02242
						10	0,409	0,0128	0,4270	4865,043	0,01719

2. Współczynnik chropowatości: k

Obliczenia dla pierwszej serii pomiarowej, pozostałe wykonane analogicznie i zestawione w tabeli 3:

Średnia wartość współczynnika chropowatości została obliczona ze średniej arytmetycznej:

Tabela 3.

Lp.	k [mm]
1	0,000102734
		2	0,000122062
		3	0,000123454
		4	0,000126516
		5	0,00016658
		6	0,00010884
		7	0,000259787
		8	0,000453653
		9	0,000291253
		10	9,76734E-05
kśr=	0,000185255

3. Zależność współczynnika oporów miejscowych
od liczby Re

Obliczenia:

Opory miejscowe:

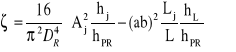
po podstawieniu wartości
i g oraz wymiarów przewodu, otrzymuje się:

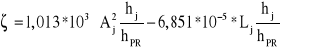
Ujemna wartość współczynnika oporów miejscowych świadczy o popełnionym błędzie grubym podczas doświadczenia.

Tabela 5. Wielkość strat miejscowych na poszczególnych elementach.

Lp.	ζ 6	ζ 8	Re
1				0,2212	0,2094	105919,492
				2	0,2091	0,2201	98208,828
				3	0,1946	0,2530	93454,432
				4	0,1848	0,2557	87638,325
				5	0,1801	0,3343	72894,522
				6	0,1625	0,2756	71996,068
				7	0,1665	0,4952	55363,253
				8	-0,2877	0,8404	38920,347
				9	-0,4266	2,1916	23331,929
				10	0,4664	35,7231	4865,043

5. Rachunek błędów

W rachunku błędów stosuję metodę różniczki zupełnej

1. Błąd w odczycie z mikromanometru:

2. Błąd prędkości:

3. Błąd współczynnika oporów liniowych:

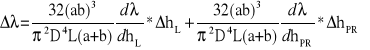
3. Błąd liczby Reynoldsa:

5. Błąd współczynnika oporów miejscowych

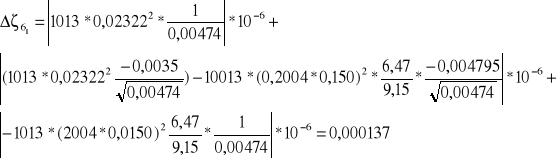
Zestawienie rachunku błędów:

Lp.	błąd v	błąd	błąd liczby Re	błąd współczynnika oporów miejscowych 6	błąd współczynnika oporów miejscowych 8
1	0,000655087	7,27641E-06	69,5006	0,000137	0,000783
2	0,000707265	8,66441E-06	75,0363	0,000245	0,000455
3	0,000743246	9,58145E-06	73,0363	0,000345	0,0008459
4	0,000792572	1,09276E-05	74,1130	0,000235	0,000456
5	0,000952879	1,63467E-05	83,5579	0,00785	0,0001465
6	0,00096477	1,5905E-05	70,3679	0,000346	0,0005654
7	0,001254617	3,01021E-05	90,3806	0,000145	0,0005332
8	0,001784662	6,63477E-05	98,8629	0,00983	0,00065443
9	0,002977022	0,000172325	115,9349	0,000872	0,0034564
10	0,014277294	0,00344	333,3130	0,000678	0,006533

6. Wnioski

Na podstawie wykonanych obliczeń możemy zauważyć następującą zależność:

• Wraz ze wzrostem przepływu wzrasta liczba Reynolds'a oraz współczynnik oporów liniowych λ w pewnym przedziale liczby Reynoldsa od ok. 4800 do ok. 38000 rośnie natomiast później maleje.

• Podczas obliczania chropowatości oraz współczynników miejscowych otrzymaliśmy wyniki ujemne. Jest to wynikiem popełnionych błędów grubych.

• Współczynnik oporów miejscowych maleje wraz ze wzrostem logarytmowanej liczby Reynoldsa dla łuku segmentowego oraz nieznacznie rośnie dla łuku.

12

---