Nr ćwiczenia 74 |
Temat ćwiczenia Polarymetr |
Ocena z teorii |
Nr zespołu 10 |
Imię i Nazwisko Miłosz Gąsiorowski |
Ocena z wykonania |
Data 20.02.2001 |
Wydział, kierunek, rok, grupa EAIiE, Automatyka i Robotyka, rok 1, gr.2 |
Uwagi |
Konspekt.
Celem ćwiczenia jest wyznaczanie kąta skręcenia płaszczyzny kąta polaryzacji oraz wykorzystanie tego zjawiska do wyznaczania stężenia roztworów cukru i grubości płytek z materiałów optycznie czynnych wpierw wzorcując przyrząd posiadanymi wzorcami.
Zapoznanie się z podstawą teoretyczną ćwiczenia.
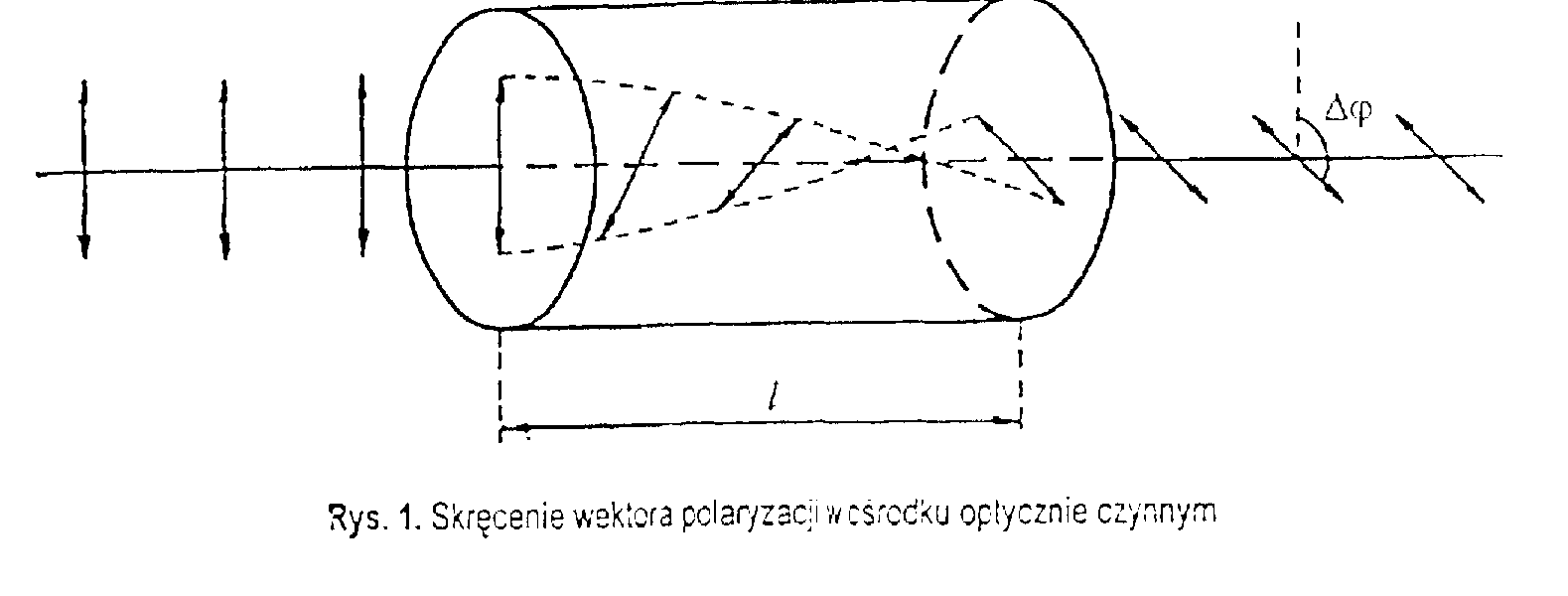
Światło liniowo spolaryzowane rozchodzi się bez zmiany płaszczyzny polaryzacji w próżni i w większości ośrodków przeźroczystych. Istnieją jednak ośrodki zwane optycznie aktywnymi, które wywołują skręcenie kierunku polaryzacji. Wektor E fali elektromagnetycznej w tych ośrodkach nie leży w jednej płaszczyźnie, lecz zatacza linie śrubową.
Skręcenie wektora polaryzacji w ośrodku optycznie czynnym
Wyjaśnienie mechanizm skręcenia wektora polaryzacji rozważyć można przy pomocy wyimaginowanej cząsteczki w kształcie śruby. Padające światło w kierunku osi y posiada pole Ey poruszające ładunkami w górę i w dół po lini śrubowej. W skutek więzów cząsteczkowych elektrony muszą pozostawać na linii śrubowej, czyli także w kierunku x .
Tak więc powstaje dodatkowa x składowa pola elektrycznego, która w wyniku superpozycji daje wypadkową zrotowaną do padającej o mały kąt
Zapoznanie się z budową przyrządu
Budowa polarymetru
Pomiar stężenia
Dla niezbyt dużych stężeń przyjąć można, że kąt skręcenia płaszczyzny polaryzacji będzie proporcjonalny do liczby cząstek, jakie napotka światło na swojej drodze. Oznacza to, że kąt skręcenia płaszczyzny polaryzacji będzie proporcjonalny do długości l i stężenia roztworu c:
k·c·l
Współczynnik proporcjonalności k nazywamy skręceniem właściwym roztworu
Dla substancji stałych możemy wykorzystać do wyznaczanie grubości płytek gdyż kąt skręcenia jest proporcjonalny do grubości:
k1·l
Wykonanie:
Ustawić położenie zerowej polarymetru.
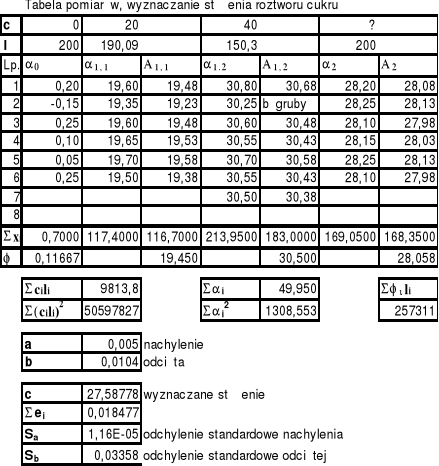
Pomiar grubości płytki (pomiar polegający na wykorzystaniu znanych wzorców):
Ustawić pusty polarymetr w pozycji zerowej- 0, powtórzyć 5-10 razy
Wyznaczyć położenie dla których pole jest zaciemnione rownomiernie- dla płytek o znanych grubościach z tego wyznaczyć kąt skręcenia płaszczyzny polaryzacji dla płytek o znanych grubościach- =0o zacząć od najcieńszej, (wykorzystując także kombinacje kilku płytek na raz, pomiar powtórzyć 5-10 razy
Wyznaczyć położenie dla których pole jest zaciemnione rownomiernie- dla płytki o nieznanej grubości, z tego wyznaczyć kąt skręcenia płaszczyzny polaryzacji dla płytki o nieznanej grubości- =0, pomiar powtórzyć 5-10 razy
Wyznaczyć prostą regresji dla otrzymanych pomiarów metoda najmniejszych kwadratów, wyliczyć współczynniki prostej.
Ze znanych współczynników regresji wyznaczyć grubość płytki.
Pomiar stężenia roztworu (pomiar polegający na wykorzystaniu znanych wzorców):
Ustawić położenie zerowe dla kuwety z rozpuszczalnikiem- 0, powtórzyć 5-10 razy
Wyznaczyć położenie dla których pole jest zaciemnione rownomiernie- dla kuwet z roztworami o znanych stężeniach z tego wyznaczyć kąt skręcenia płaszczyzny polaryzacji dla płytek o znanych grubościach- =0 zacząć od najcieńszej, pomiar powtórzyć 5-10 razy
Wyznaczyć położenie dla których pole jest zaciemnione rownomiernie- dla kuwety z roztworem o nieznanym stężeniu, z tego wyznaczyć kąt skręcenia płaszczyzny polaryzacji dla kuwety z roztworem o nieznanym stężeniu - =0, pomiar powtórzyć 5-10 razy
Wyznaczyć prostą regresji dla otrzymanych pomiarów metoda najmniejszych kwadratów, wyliczyć współczynniki prostej.
Ze znanych współczynników regresji wyznaczyć stężenie roztworu.
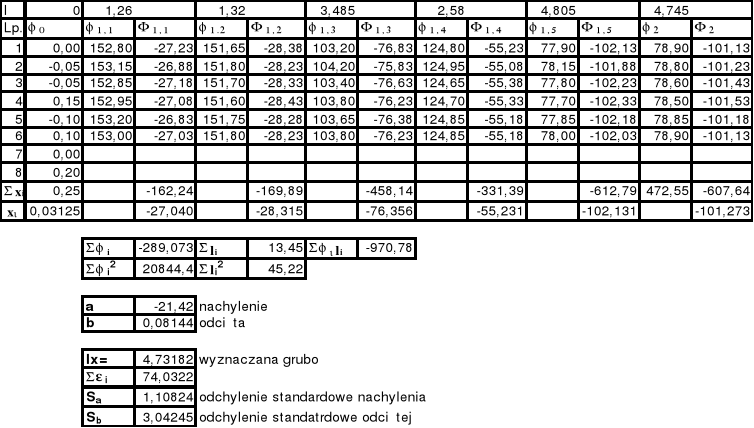
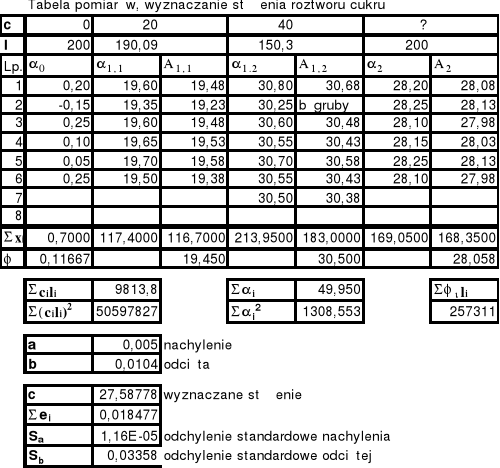
Ocena błędów oraz wyniki pomiarów.
Stosujemy metodę wyrównawczą Gaussa do analizy wyników (wynik zastosowania metody najmniejszych kwadratów):
![]()
Ogólna zależność wyników w zależności liniowej:
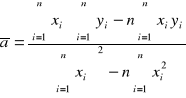
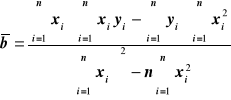
Wzory na wyliczenie współczynników zależności liniowej, mając n par punktów pomiarowych xi yi zależnych liniowo.
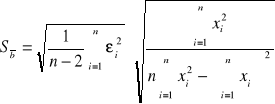
Sposób wyliczenia odchylenia standardowego:
![]()
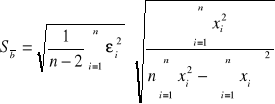
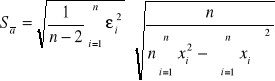
![]()
Jeżeli znajdziemy współczynniki a i b oraz znając obliczymy l oraz odchylenie standardowe Sa gdyż
![]()
![]()
identycznie jeżeli będziemy znali średnie obliczymy stężenie cx
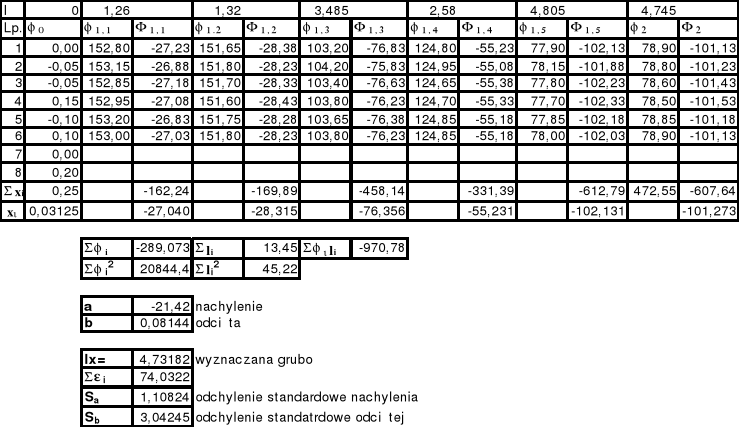
Błąd wyznaczanie zarówno stężenia roztworu jak i grubości płytek kwarcowych zależy od kilku zmiennych tak wiec błędy będziemy wyznaczać metodą różniczki zupełnej. Sam błąd pomiar kąta wynika przy ocenianiu różnic oświetlenia płytki Laurenta. W takich przypadkach słuszne jest prawo psycho-fizjologiczne związane z budową oka (prawo Webera-Fechnera), mówiące że bezwzględną różnicą oświetleń E którą oko może zauważyć, jest proporcjonalna do wielości oświetlenia E=kE , k współczynnik proporcjonalności. W zasadzie pomiar był przeprowadzany tak, że polaryzator i analizator były skręcone o 90o, więc oświetlenie było minimalne, ale występowały różnice pomiędzy poszczególnymi płytkami SiO2 najjaśniejsze światło było dla płytki najcieńszej, oczywiście ze względu na najmniejszy współczynnik pochłaniania zależny od grubości. Dużą trudność sprawiało znalezienie miejsca równooświetlonej płytki Laurenta dla kombinacji wielu płytek, gdyż następowała kumulacja błędu wprowadzanego przez zanieczyszczenia na powierzchniach płytek kwarcowych.
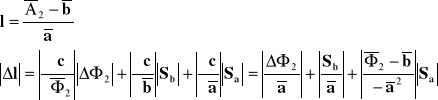
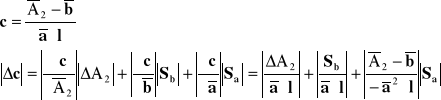
Wyliczenie błędów wyznaczanych wielkości metodą różniczki zupełnej:
Wnioski?
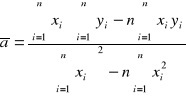
![]()
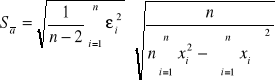
![]()
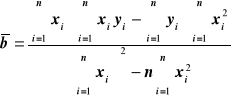
![]()
![]()
![]()
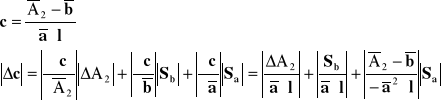
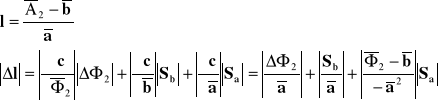
Wyszukiwarka
Podobne podstrony:
Fizyka 1, AGH, i, Laborki, Laborki, Lab, FIZYKA - Laboratorium, WAHADŁA FIZYCZNE
Fizyka 14b, AGH, agh, programinski, Laborki, Laborki, Lab, FIZYKA - Laboratorium, fiz lab, franko
Polarymetr Laurenta, AGH, agh, programinski, Laborki, Laborki, Lab, FIZYKA - Laboratorium, Polarymet
cw82 - Efekt fotoelektryczny, AGH, i, Laborki, Laborki, Lab, FIZYKA - Laboratorium, Struna i Krzychu
cw 13 - Lepkosc, AGH, agh, programinski, Laborki, Laborki, Lab, FIZYKA - Laboratorium, Struna i Krzy
TERMOPAR, AGH, i, Laborki, Laborki, Lab, FIZYKA - Laboratorium, lab-fizyka, Wyznaczanie temperatury
FIZYKA~6, AGH, agh, programinski, Laborki, Laborki, Lab, FIZYKA - Laboratorium, lab-fizyka, Moduł sz
cw 3 - Wahadlo Rewersyjne, AGH, i, Laborki, Laborki, Lab, FIZYKA - Laboratorium, Struna i Krzychu
LAB31+, AGH, i, Laborki, Laborki, Lab, FIZYKA - Laboratorium, kondensator
Fizyka 9, AGH, agh, programinski, Laborki, Laborki, Lab, FIZYKA - Laboratorium, fiz lab, franko
cw41 - Busola Stycznych, AGH, agh, programinski, Laborki, Laborki, Lab, FIZYKA - Laboratorium, Strun
FIZYK~51, AGH, agh, programinski, Laborki, Laborki, Lab, FIZYKA - Laboratorium, SOCZEWKI
FIZ5=, AGH, agh, programinski, Laborki, Laborki, Lab, FIZYKA - Laboratorium, 052 zalamanie dla ciecz
Fizyka 12b, AGH, agh, programinski, Laborki, Laborki, Lab, FIZYKA - Laboratorium, fiz lab, franko
więcej podobnych podstron