PRACOWNIA ZAKŁADU FIZYKI PL
Radosław Michałek		Wydział Elektryczny Grupa EDi 2.1
Data wykonania ćwiczenia: 1999-03-03	Numer ćwiczenia: E 6.1	Temat ćwiczenia: Zjawisko rezonansu elektrycznego
Zaliczenie:	Ocena:	Data:	Podpis:

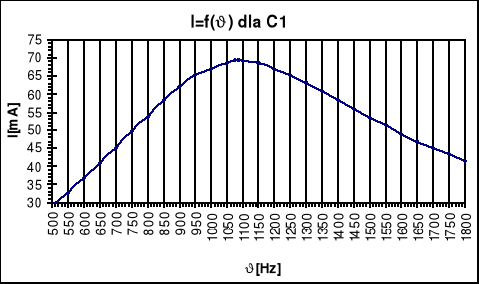
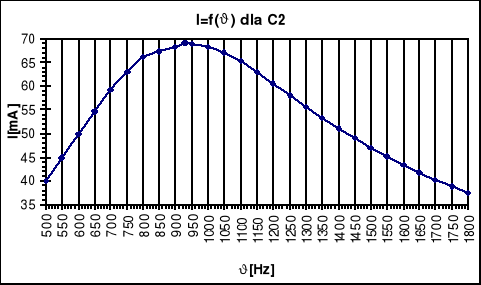
1. Tabela pomiarów

L.p	υ	I		L.p	υ	I
-	Hz	mA		-	Hz		mA
1	500	29		1	500		40
2	550	32,8		2	550		44,9
3	600	36,7		3	600		49,8
4	650	40,9		4	650		54,6
5	700	45,2		5	700		59,1
6	750	49,7		6	750		63
7	800	53,7		7	800		66,1
8	850	58,3		8	850		67,2
9	900	62,1		9	900		68,3
10	950	65,2		10	925		69,1
11	1000	67,1		11	930		69,1
12	1050	68,5		12	931		69,1
13	1075	69,5		13	950		68,8
14	1084	69,5		14	1000		68,2
15	1087	69,5		15	1050		67
16	1100	69		16	1100		65,2
17	1150	68,5		17	1150		63
18	1200	67,1		18	1200		60,6
19	1250	65,3		19	1250		58
20	1300	63,2		20	1300		55,6
21	1350	60,8		21	1350		53,3
22	1400	58,3		22	1400		51,1
23	1450	55,9		23	1450		49
24	1500	53,4		24	1500		47
25	1550	51,2		25	1550		45,1
26	1600	49		26	1600		43,4
27	1650	47		27	1650		41,8
28	1700	45,1		28	1700		40,3
29	1750	43,2		29	1750		38,8
30	1800	41,6		30	1800		37,5

2. 
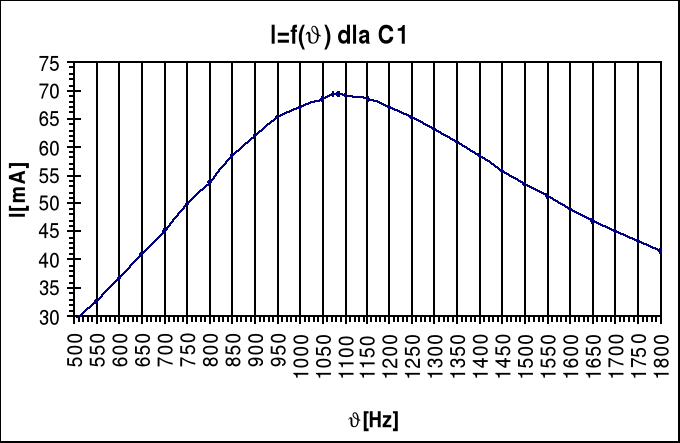
   Wykresy




3. Obliczenia

C₁=1,3*10^-6 F ν_r1=1084 Hz

C₂=1,8*10^-6 F ν_r2=930 Hz




L - indukcyjność

C - pojemność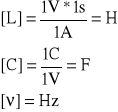


ν - częstotliwość

4. Krótka teoria

Zjawisko rezonansu napięć przedstawia taki stan pracy obwodu elektrycznego, przy którym reaktancja wypadkowa obwodu jest równa zeru. W stanie rezonansu napięcie i prąd na zaciskach rozpatrywanego obwodu są zgodne w fazie, tzn. argument impedancji zespolonej obwodu jest równy zeru(ϕ=0). Obwód będący w stanie rezonansu nie pobiera za źródła mocy biernej, następuje zjawisko kompensacji mocy. Moc bierna indukcyjna pobierana przez obwód jest równa mocy biernej pojemnościowej. Ponieważ znaki mocy biernej indukcyjnej i pojemnościowej są przeciwne, dlatego w warunkach rezonansu całkowita moc bierna obwodu jest równa zeru.

Częstotliwość, przy której reaktancja wypadkowa obwodu jest równa zeru nazywana jest częstotliwością rezonansową. Obwód elektryczny osiąga stan rezonansu, jeśli częstotliwość doprowadzonego do obwodu napięcia sinusoidalnego jest równa częstotliwości rezonansowej.




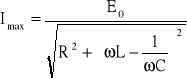
a w rezonansie ωL=1/ωc to





Kąt przesunięcia fazowego :




5. Wykonanie ćwiczenia

W celu przeprowadzenia pomiarów zestawiamy obwód taki, jak na rysunku:




Obwód składa się z kondensatora C (C1 i C2), miliamperomierza oraz cewki L, której indukcyjność L wyznaczamy. Źródłem zasilania jest generator drgań sinusoidalnych o regulowanej częstotliwości. Zmieniając częstotliwość obserwujemy oraz zapisujemy zmiany prądu płynącego w obwodzie. Prąd maksymalny będzie płynął przy częstotliwości rezonansowej. Pomiary przeprowadzamy dla dwóch różnych wartości kondensatora.

6. Opracowanie wyników pomiarów

Błąd względny maksymalny - metoda różniczkowa uproszczona




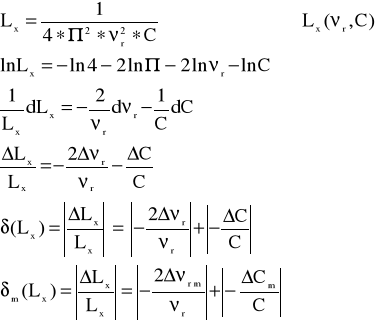
Kondensator

C1 zakres - 1μF 0,3μF

klasa - 0,1% 0,5%

C2 zakres - 1μF 0,8μF

klasa - 0,1% 0,5%

ΔC _max=ΔC'+ΔC''

ΔC' i ΔC'' - błędy wynikające z klasy niedokładności poszczególnych zakresów dekady kondensatora


ΔC1_max=1*10^-9F + 1,5*10^-9F=2,5*10^-9F


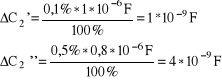
ΔC2_max=1*10^-9F + 4*10^-9F=5*10^-9F

Amperomierz

zakres - 200mA

klasa - 1

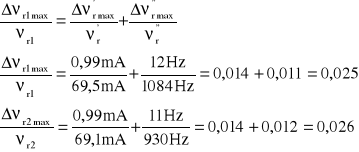
Δν_rm=Δν_r'+Δν_r''

Δν_r' - błąd bezwzględny pomiaru wynikający z klasy niedokładności miernika

Δν_r'' - błąd równy maksymalnemu przedziałowi częstotliwości, przy którym (w momencie rezonansu) wskazania miliamperomierza nie ulegają zmianie.

Δν_r'=klasa*wskazanie+3c , c=0,1mA

Δν_r1'=1%*69,5 mA+3*0,1mA=0,695mA+0,3mA=0,99mA

Δν_r1''=1087Hz-1075Hz=12Hz

Δν_r2'=1%*69,1 mA+3*0,1mA=0,691mA+0,3mA=0,99mA

Δν_r2''=931Hz-925Hz=11Hz







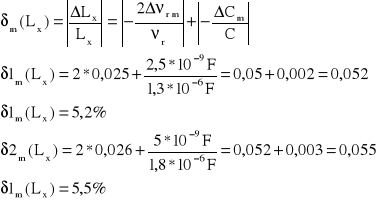
1

2







---