uplastycznienie w pobliŻu wierzchoŁka szczeliny

Sprężysto-plastyczne pole naprężeń w pobliżu wierzchołka szczeliny

Model Irwina

Zakładając, że materiał jest idealnie sprężysto-plastyczny naprężenia nie mogą przekroczyć wartości granicy plastyczności σ_ys. Rozkład naprężeń musi być taki, aby w strefie przywierzchołkowej naprężenia były stałe i równe σ_ys, a poza tą strefą malały wraz z oddalaniem się od wierzchołka szczeliny. Problem sprowadza się do wyznaczenia długości strefy plastycznej r_p oraz rozkładu naprężeń poza tą strefa.

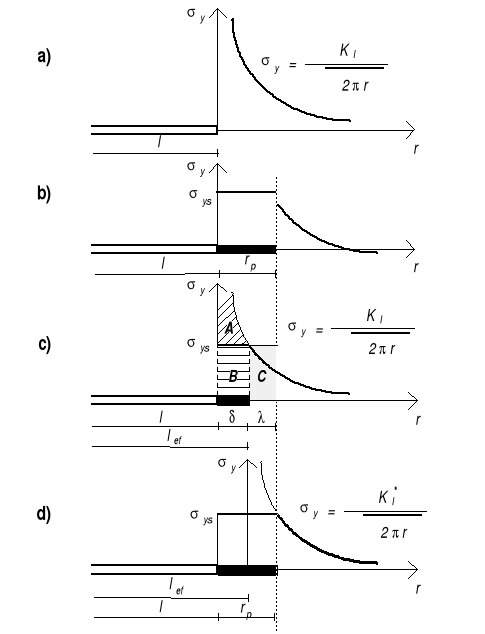
Koncepcja Irwina : rozkład ten może być uzyskany w oparciu o osobliwy, sprężysty rozkład naprężeń poprzez "obcięcie" tego wykresu na poziomie σ_y =σ_ys. Jest to tzw. pierwsze przybliżenie przyjmuje się, że strefa plastyczna ma długość , która wynika z warunku :

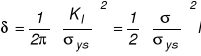
Niezrównoważone naprężenia w obszarze A



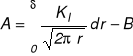
Niezrównoważoną siłę A równoważymy poprzez powiększenie długości strefy plast. o odc. , co jest równoważne poszerzeniu prostokątnego, plastycznego rozkładu naprężeń o obszar C.

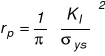
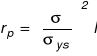
W płaskim stanie odkształcenia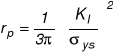

Rozkład naprężenia poza strefą plastyczną.

Irwin wprowadził pojęcie tzw. szczeliny zastępczej o długości efektywnej

l ef = l +

Na skutek tej "fikcyjnej" zmiany długości szczeliny zmienia się wartość WIN

Zmodyfikowany rozkład naprężeń sprężystych poza strefą plastyczna o długości rp

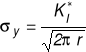
Model Dugdale 'a

Schematyzacja sprężysto-plastycznego zachowania się szczeliny zaproponowana przez Dugdale'a również bazuje na czysto sprężystych rozwiązaniach dotyczących pola naprężeń i przemieszczeń. U podstaw modelu leżały obserwacje doświadczalne zachowania się szczeliny w cienkiej blasze ze stali miękkiej. Dugdale stwierdził, że uplastycznienie w pobliżu wierzchołka szczeliny objawia się powstaniem krzyżowych płaszczyzn poślizgu, nachylonych pod katem 45° do płaszczyzny blachy. Wysokość strefy plast. jest więc równa grubości blachy t. Zakładając, że grubość jest znikomo mała w stosunku do pozostałych wymiarów blachy, a także długości strefy plast., Dugdale przyjął, że prostokątny kształt strefy plastycznej można aproksymować odcinkiem. Model Dugdale'a dotyczy wyłącznie plaskiego stanu naprężenia.

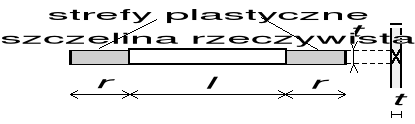
Koncepcyjnie model Dugdale'a jest podobny do modelu Irwina, gdyż i tu strefę plastyczną traktuje się jak część "nowej" szczeliny, tzw. szczeliny zastępczej o długości równej sumie długości szczeliny rzeczywistej i strefy plastycznej . Strefę plastyczną usuwa się myślowo z materiału, tworząc fikcyjną szczelinę do powierzchni której przykłada się obciążenie wywołane oddziaływaniem "odrzuconej" części materiału, równe granicy plastyczności σ_ys.

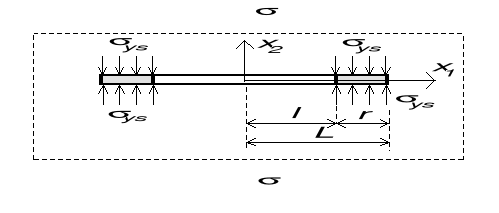
Warunki "brzegowe":

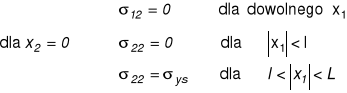
Założenie : ciało zachowuje się jak ośrodek liniowo sprężysty, a uplastycznienie strefy brzegowej jest uwzględniane jedynie poprzez jej obciążenie σ_ys.

Skutek : możliwe jest zastosowanie zasady superpozycji.

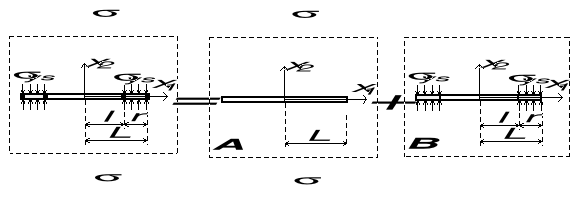
Metoda Westergaarda

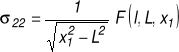
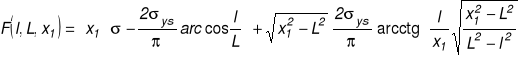
Warunek skończonej wartości naprężenia w wierzchołku szczeliny zastępczej:

Długość strefy plastycznej

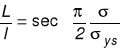
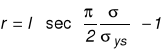
Rozwijając funkcję sec w szereg potęgowy i biorąc jedynie pierwszy wyraz rozwinięcia, :

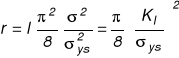
Rozkład naprężenia σ₂₂

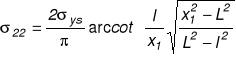
Kształt stref plastycznych

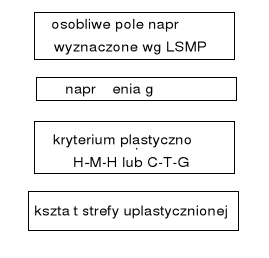
Algorytm wyznaczania strefy plastycznej w pobliżu wierzchołka szczeliny.

Kryterium wytężeniowe Hubera-Misesa-Hencky'ego

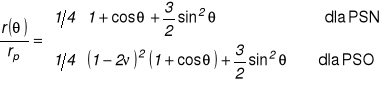
gdzie

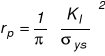
Dla =0 (wzdłuż osi szczeliny x1) i dla = 1/3

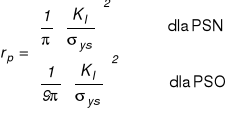
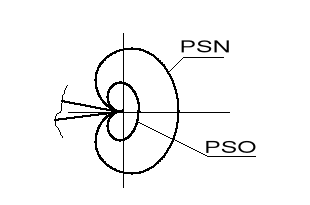
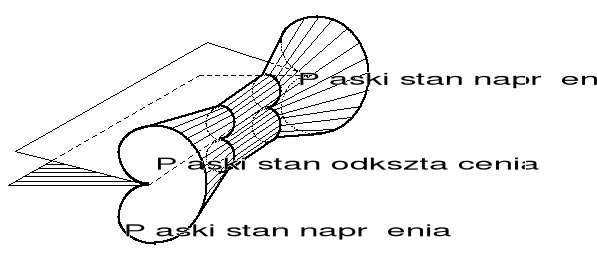
Kształt stref plastycznych dla PSN i PSO

Grubość ciała, a kształt strefy plastycznej

Za miarodajne oszacowania strefy plastycznej wzdłuż osi szczeliny przyjmuje się związki:

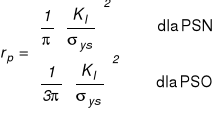
Na podstawie badań przyjęto, że PSN jest dominujący gdy zachodzi związek:

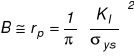
Warunek PSO, zgodnie z normą amerykańską - ASTM E-399-81

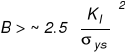
PRZYKŁAD 1

Odporność materiału na pękanie (krytyczny współczynnik intensywności naprężeń) wynosi
KIc = 80 MPa m^1/2, a granica plastyczności σ_ys = 410 MPa. Uwzględniając uplastycznienie w wierzchołku szczeliny w warunkach płaskiego stanu odkształcenia wyznaczyć "poprawkę" w wartości odporności na pękanie.

Rozwiązanie:

Długość strefy plastycznej w warunkach PSO wynosi

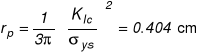
"Poprawiona" (efektywna) wartość odporności na pękanie wyraża się zależnością

a wyjściowa odporność związkiem

zachodzi zatem relacja

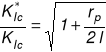
Weźmy szczelinę o dowolnej długości np. l = 2.5 cm

Tak więc uwzględnienie poprawki plastycznej spowodowało 4% wzrost odporności na pękanie.

MECHANIKA PÊKANIA.

Uplastycznienie w pobliżu wierzchołka szczeliny 6

65

---