Wprowadzenie do systemów telekomunikacyjnych

Temat: Podstawowe charakterystyki analogowych sygnałów telekomunikacyjnych

Autor: Błażej Zięba

I. Pojęcie sygnału

Pojęcie sygnału wiąże się ściśle z systemami telekomunikacyjnymi. Obieg informacji w systemie telekomunikacyjnym zachodzi dzięki przesyłaniu i przetwarzaniu wielkości elektrycznych (bądź np. akustycznych, optycznych itd.) zawierających informację czyli sygnałów.

Pojęcie sygnału należy jednak rozszerzyć o różne inne przebiegi elektryczne o charakterze pomocniczym , jak na przykład zasilające , nośne synchronizujące. Ponad to niezależnie od użytkowników i twórców systemu telekomunikacyjnego w systemie pojawiają

się i na system oddziaływają z zewnątrz niepożądane przebiegi zakłócające (np. szumy, sygnały z innych systemów). W poniższym wykładzie pojęcie sygnału będzie traktowane w sensie „szerokim” (sygnały pomocnicze sygnały informacyjne, sygnały zakłócające).

II. Przebieg czasowy sygnału i jego analiza

Przebieg czasowy sygnału uważa się za jego postać naturalną. Traktuje się sygnały przede wszystkim jako funkcje argumentu rzeczywistego czasu i w tym sensie mówi się o „wartości sygnału”. Przebieg czasowy sygnału należy traktować jako punkt wyjścia do innych przekształceń, tak więc sygnały istniejące obiektywnie w rzeczywistości fizycznej lub technicznej mogą być badane doświadczalnie.

Najprościej jest w tym celu dokonać pomiarów wartości sygnałów x(t) stanowiącego np. rzeczywisty ciąg funkcji czasu, otrzymamy wówczas tablicę par wartości {t;x(t)}punktowo charakteryzującą przebieg tej funkcji. Inną metodą poznawczą jest modelowanie danego układu lub systemu, należy wówczas przedstawić strukturę fizyczną jako zespół idealizowanych elementów i pobudzeń, wyrazić na podstawie praw fizyki relacje między nimi i w ten sposób dochodzić do równań matematycznych zawierających funkcję czasu opisujących sygnały bez ograniczeń czasu trwania i dokładności. Zbiór wartości sygnałów fizycznych istniejących i badanych doświadczalnie jest ciągłym podzbiorem ,przedziałem na osi liczb rzeczywistych x∈R(a,b), jednakże przy matematycznym modelowaniu sygnału niezbędne niekiedy jest założenie x∈R(-∞,∞). Wszelkie sygnały istniejące w rzeczywistości oraz niektóre sygnały modelowane opisuje się przy użyciu zbiorów ograniczonych |t|<∞ ; |x|<∞ . Jeżeli funkcja czasu opisująca sygnał znika (tożsamościowo równa się zero), a poza domkniętym przedziałem x(t)=0, t∈[a,b]. Przedział argumentu [a,b] nazywamy wyznacznikiem sygnału o trwaniu ograniczonym. Analogicznie tworzy się pojęcie sygnału o ograniczonym zakresie wartości. Wobec tego modele sygnałów można podzielić na cztery klasy wg następującego schematu klasyfikacji.

		Zakres wartości
Czas trwania	ograniczony	ograniczony	nieograniczony
	nieograniczony	ograniczony	nieograniczony

III. Energia i moc

Powszechnie przyjętą konwencją teoretyczną jest wyznaczenie mocy sygnału
(prądowego lub napięciowego) na jednostkowej rezystancji. Wówczas moc chwilową P_t(t) jest równa kwadratowi wartości chwilowej sygnału.

P_t(t)=x²(t)

Energia sygnału:

W(T)=

Klasyfikacja sygnałów wg cech energetycznych

Sygnały o energi ograniczonej	Sygnały o energii nieograniczonej
	| Sygnały o mocy średniej ograniczonej	| Sygnały o mocy średniej nieograniczonej

W dziedzinie czasu można wykonywać na sygnałach-funkcjach działania algebraiczne i operacje analityczne. Analiza i algebra sygnałów ciągłych jest całkowicie konwencjonalna. W szczególności definiuje się operacje uśredniania czasowego w celu wyznaczenia:

Wartości średniej:
=

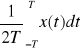
Wartości średnio kwadratowej:
=

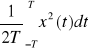
Wartości skutecznej : x_sk=
^1/2= [

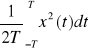
]^1/2

IV. Analiza częstotliwości

Bardzo istotną rolę odgrywa opis sygnałów w dziedzinie częstotliwości od postaci naturalnej przechodzi się do zapisu pośredniego opartego z reguły na rozwinięciach i przekształceniach Fouriera. Analiza cech częstotliwościowych umożliwia prawidłowe dopasowanie sygnałów do torów transmisyjnych i odwrotnie. Sygnał x(t) można przedstawić za pomocą wzoru całkowego Fouriera:

x(t)=

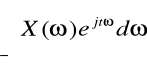
przy czym X(ω) jest transformatą Fouriera sygnału x(t):

X(ω)=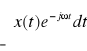

Przekształcenie całkowe zapisujemy w skrócie:

x(t)
X(ω)

Transformatą Fouriera jest funkcja widmowa określona w dziedzinie częstotliwości lub pulsacji.

Biegunowe składowe funkcji widmowej

X(ω)=|X(ω)|exp{arg[X(ω)]}

nazywają się odpowiednio:

widmo amplitudowe |X(ω)|

widmo fazowe φ(ω)= arg[X(ω)]

W całej dziedzinie ω∈(-∞,∞) widmo amplitudowe jest parzyste, a widmo fazowe nieparzyste.

Dla funkcji o energii ograniczonej jego składowe są ciągłe można wiec te składowe interpretować jako widmo gęstości amplitud i faz.

Korzystając ze wzoru Perssevalla

W=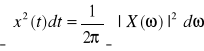

Można stwierdzić, że |X(ω)|² ma sens gęstości energii w dziedzinie pulsacji i nazywa się widmem (gęstości) energii o wymiarze [J/m/s]

Przykład sygnału o skończonej energii: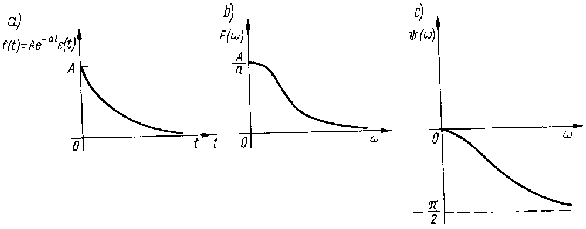

Sygnały o nieskończonej energii

Funkcja rzeczywista x(t) całkowalna bezwzględnie w przedziale [t₀,t₀+T] jest w tym przedziale rozwijalna w szereg nieskończony Fouriera.

x(t)=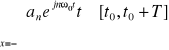

przy czym pulsacja podstawowa ω₀=
, a współczynniki zespolone są równe

a_n=

e^jnωtdt

Na tej podstawie wyznaczamy widmo zespolonej funkcji okresowej x(t)=x(t+nT)

Przekształcając i transformując powyższe wyrażenie otrzymujemy widmo prążkowe


X(ω)=ω₀
(ω-nω₀)

Przy czym zespoloną wagę n-tego prążka wyznaczamy ze wzoru

X_n=Ta_n=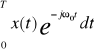

Przykład sygnału o energi nieskończonej:

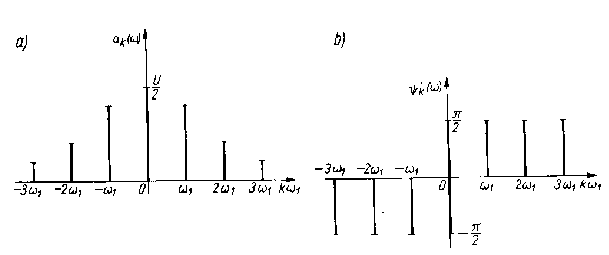
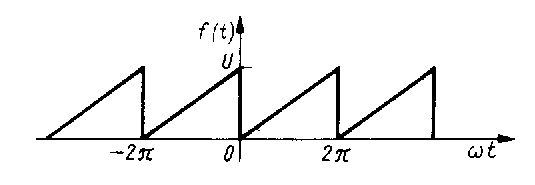
Wychodząc z definicji mocy dla sygnałów rzeczywistych rozważmy rozkład mocy średniej w dziedzinie częstotliwości, aby z sygnału o mocy ograniczonej x(t) utworzyć sygnał o energii ograniczonej należy pobrać jego wycinek obcięty przy ± T, czyli x_T(t), t∈(-T,T). Mamy wówczas

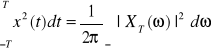
Przejście graniczne T→∞ rekonstruuje całość sygnału x(t) i otrzymamy moc średnią

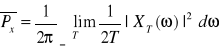
Widać wyraźnie, że funkcja podcałkowa stanowi widomą gęstość mocy o wymiarze [W/
], oznaczaną przez S_x(ω)

S_x(ω)=

Jeżeli granica istnieje, gęstość mocy jest funkcją rzeczywistą, nieujemną parzystą. Moc sygnału jest całką z gęstości mocy w całej dziedzinie pulsacji, ω- ze współczynnikiem 1/2π

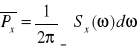
V. Klasyfikacja sygnałów i ich modeli według cech częstotliwościowych

	Sygnały rzeczywiste
Sygnały o widmie ciągłym ω∈R	Sygnały o widmie prążkowym ω∈D	Sygnały o widmie złożonym (część ciągła + prążki)

	Sygnały rzeczywiste
Sygnały monochromatyczne |ω|=const	Sygnały pasmowe |ω|∈(ω1,ω2)	Sygnały wszechpasmowe |ω|∈(-∞,∞)

Reasumując można opisywać i analizować w dziedzinie częstotliwości dowolne sygnały zdeterminowane. Prawie zawsze można wyznaczyć zespolone widmo fourierowskie, które zawiera, które zawiera - w części ciągłej lub/i w prążkach - cała informację o sygnale. Odnośne widmo (gęstości) energii jest już pozbawione informacji typu fazowego. Widmo (gęstości) mocy może być wyznaczane jedynie dla sygnałów o niezerowej mocy średniej i jest również pozbawione informacji fazowych.

---