1. Geometria elipsoidy obrotowej jako powierzchni odniesienia w geodezji; współrzędne prostokątne i krzywoliniowe (geodezyjne) oraz ich wzajemne relacje.
Elipsoida obrotowa:
jest powierzchnią przybliżającą kształt Ziemi
pozwala na proste rozpatrywanie związków matematycznych sieci geodezyjnych
pozwala na odwzorowanie powierzchni elipsoidy na płaszczyznę w celu sporządzenia map
Kształt i rozmiar elipsoidy:
posiada dwie półosie: dłuższa równikowa a≈6378km; krótsza biegunowa b
do określenia kształtu potrzebne są: dwa elementy liniowe (a, b; a-b≈20 km)
lub jeden element liniowy i element kształtuelementy kształtu elipsoidy obrotowej:
spłaszczenie
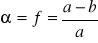
pierwszy i drugi mimośród
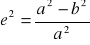
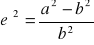
środek układu w środku elipsoidy obrotowej
płaszczyzna XY leży na płaszczyźnie tworzonej przez półosie a (płaszczyzna równika)
płaszczyzna XZ pokrywa się z płaszczyzną południka L0
szerokość geodezyjna B - kąt jaki tworzy normalna do elipsoidy w punkcie z płaszczyzną równika geodezyjnego; wartości od +90º do -90º (na równiku B=0)
południk krawędź przecięcia powierzchni elipsoidy z płaszczyzną zawierającą półosie b (oś Z)
długość geodezyjna L - kąt pomiędzy płaszczyzną południka początkowego a płaszczyzną południka zawierającego dany punkt; wartości od +180º do -180º (E, W) lub od 0º do 360º E
Wysokość H odległość od powierzchni elipsoidy do punktu po linii normalnej do elipsoidy
B, L, H→ x, y, z
x, y, z→ B, L, H (metoda Hirvonena- kolejność obliczeń)
Promień równoleżnika
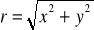
pierwsze przybliżenie B
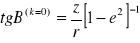
N i H dla aktualnego N
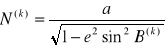
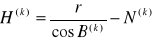
Kolejne przybliżenie B
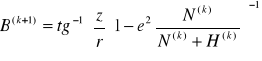
Jeżeli B(k+1)-B(k)<0,0001” niespełnione to powrót do podpunktu c; jeżeli spełnione to:
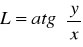
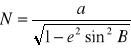
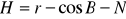
Współrzędne prostokątne:
Współrzędne krzywoliniowe:
Zależności :
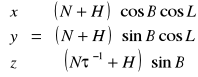
gdzie ![]()
i ![]()
4. Układ współrzędnych geograficznych astronomicznych. Trójkąt paralaktyczny.
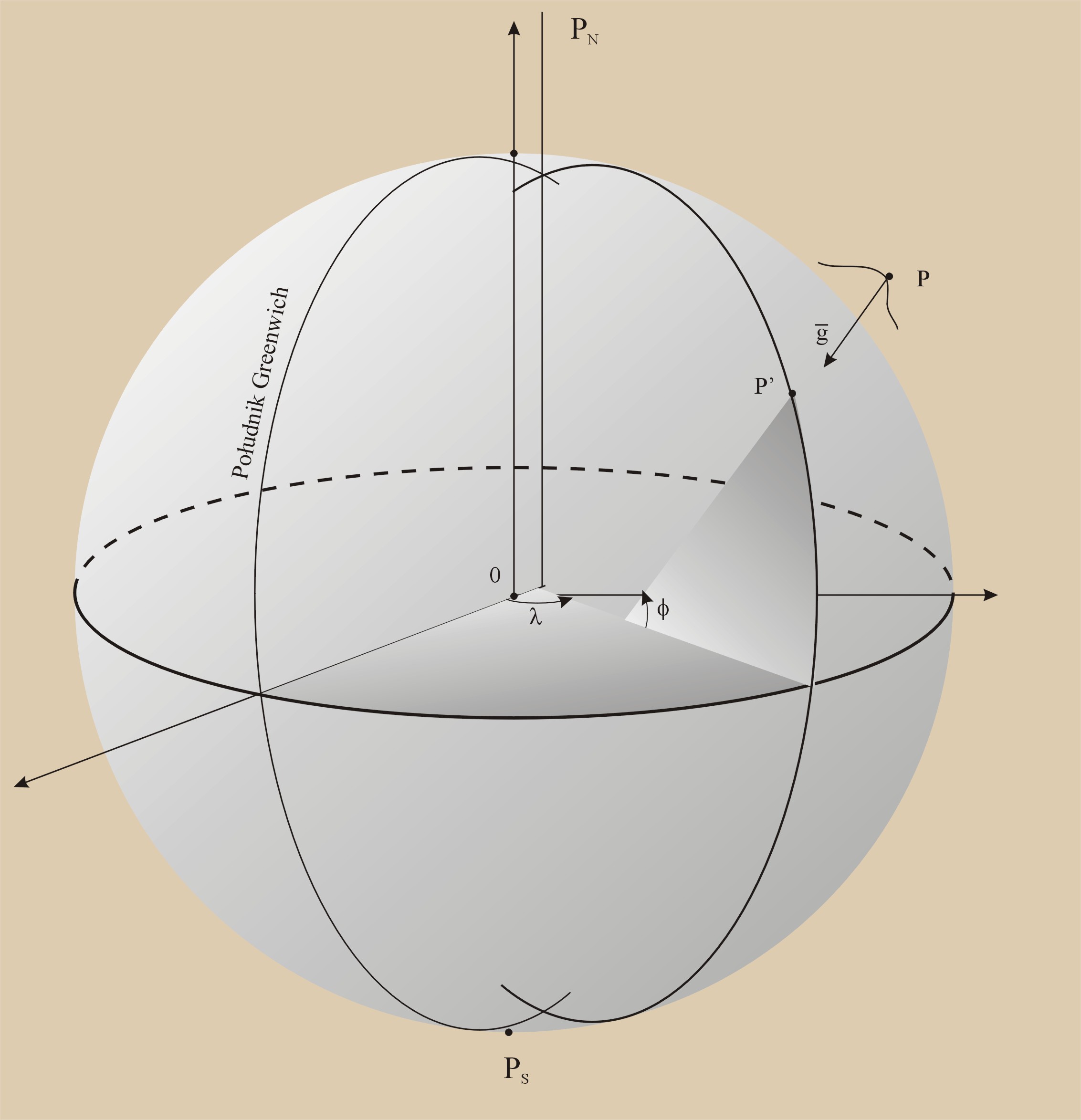
Początek układu w środku mas Ziemi
g- wektor przyspieszenia siły ciężkości w punkcie
f- kąt zawarty pomiędzy kierunkiem siły ciężkości i płaszczyzną równika; wartości od +90º do -90º (lub N, S)
l- kąt dwuścienny zawarty pomiędzy płaszczyzną południka zerowego (przyjęty Greenwich) i płaszczyzną południka zawierającą punkt; wartości od +180º do -180º (lub E, W)
Trójkąt paralaktyczny
Jest to trójkąt sferyczny o wierzchołkach w: biegunie niebieskim, zenicie i gwieździe
Oznaczenie Kąt w wierzchołku Kąt naprzeciw wierzchołka
PN- biegun niebieski t (kąt godzinny) kąt zenitalny=90 º-h(wysokość)
Z- zenit 360 º-AN(azymut na gwiazdę) 90 º-d(deklinacja)
G- gwiazda q(kąt paralaktyczny) 90 º-F(szerokość geogr.)
Znając 3 wielkości trójkąta jesteśmy w stanie obliczyć pozostałe jego elementy
Wyszukiwarka
Podobne podstrony:
7-Wpływ stosunku bazowego na dokładność opracowania wysokościowego, Geodezja PW, Stare dzieje, Egzam
Ogólne opracowanie zagadnień z fotki, Geodezja PW, Stare dzieje, Egzamin inż, Fotka - odpowiedzi
GW - 24, Geodezja PW, Stare dzieje, Egzamin inż, GW - odpowiedzi
GW-16, Geodezja PW, Stare dzieje, Egzamin inż, GW - odpowiedzi
GW - 27, Geodezja PW, Stare dzieje, Egzamin inż, GW - odpowiedzi
GW - 8, Geodezja PW, Stare dzieje, Egzamin inż, GW - odpowiedzi
GW - 31, Geodezja PW, Stare dzieje, Egzamin inż, GW - odpowiedzi
GW - 22, Geodezja PW, Stare dzieje, Egzamin inż, GW - odpowiedzi
GW - 12, Geodezja PW, Stare dzieje, Egzamin inż, GW - odpowiedzi
GW - 30, Geodezja PW, Stare dzieje, Egzamin inż, GW - odpowiedzi
GW - 29, Geodezja PW, Stare dzieje, Egzamin inż, GW - odpowiedzi
GW - 3, Geodezja PW, Stare dzieje, Egzamin inż, GW - odpowiedzi
więcej podobnych podstron