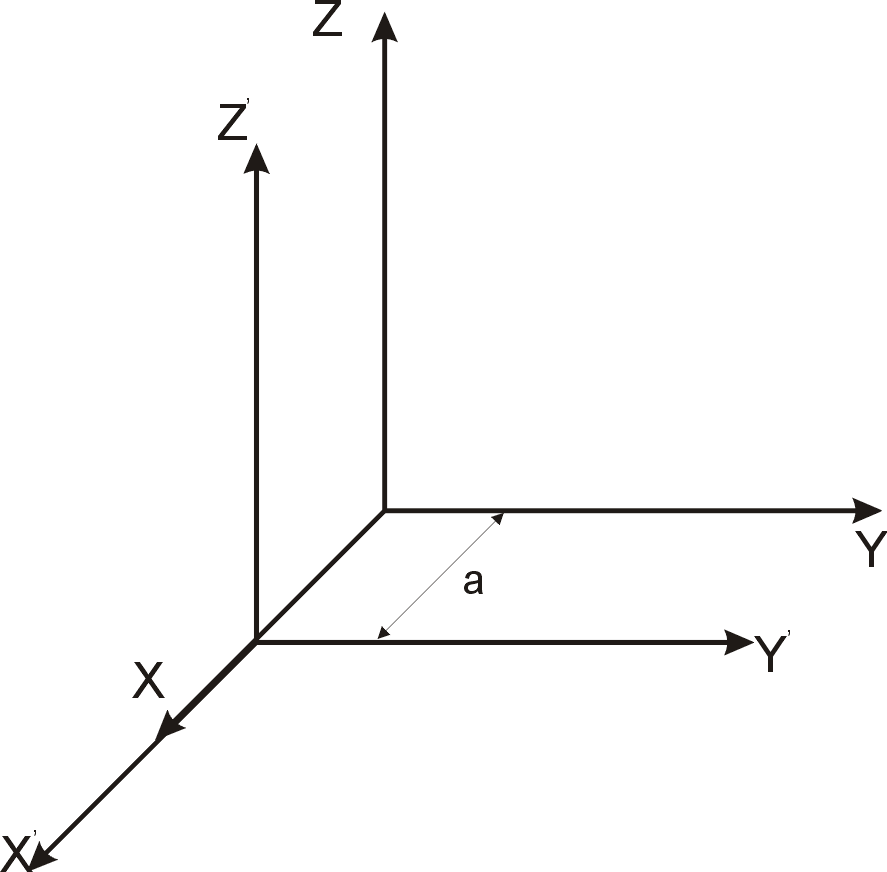
Ruch ciała sztywnego w przestrzeni euklidesowej.
Załóżmy, że zwarty podzbiór ![]()
oznacza ciało sztywne zgodnie z poniższym rysunkiem:
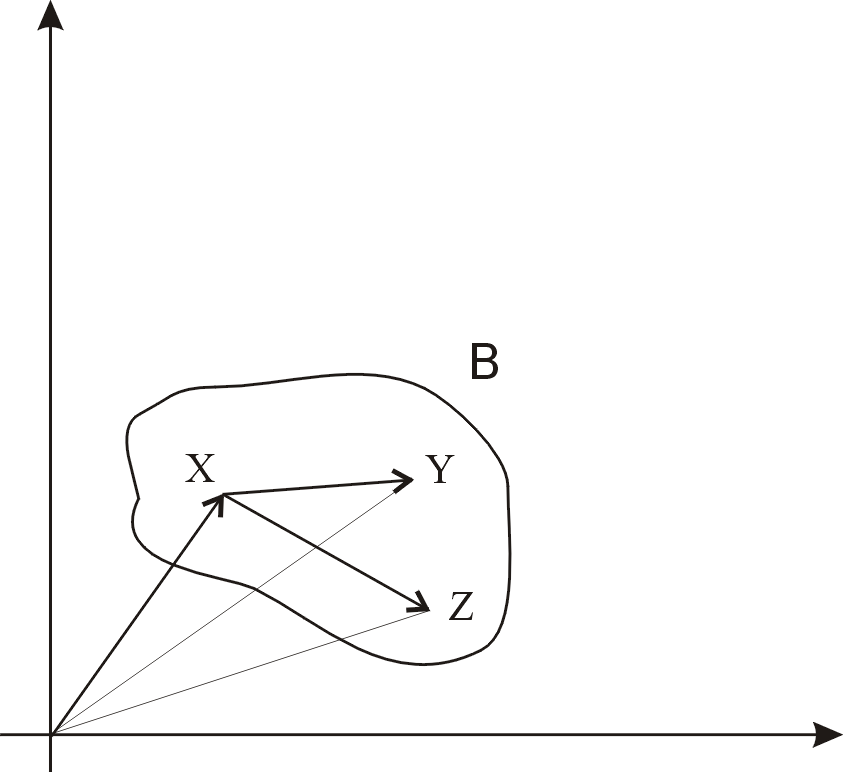
Wybierając punkty x,y,z ![]()
B i definiując wektory swobodne jako:
v = y - x oraz w = z -x łączące punkt x z punktami y i z, możemy afiniczne przekształcenie: ![]()
gdzie: ![]()
przenieść na wektory swobodne określając:
![]()
. Przekształcenie to nazywamy przemieszczeniem ciała sztywnego w przestrzeni euklidesowej, jeżeli D* zachowuje iloczyn skalarny i iloczyn wektorowy, tzn.: ![]()
( inwariantność (niezmienniczość)), ![]()
( ekwiwariantność (równozmienność)). Na mocy definicji, przemieszczenie ciała sztywnego zachowuje długość wektorów swobodnych (odległość między punktami) oraz kąt miedzy wektorami swobodnymi tj: ![]()
.Uwzględniając podane definicje i właściwości przemieszczenie ciała sztywnego w przestrzeniu euklidesowej możemy opisać następującą charakterystyką: 1.macierz R jest ortogonalna tj. RRT = RTR == I3; 2.![]()
; 3.![]()
; 4. Wektor T (przesunięcie) jest dowolny.
Macierze R spełniające pierwsze trzy warunki nazywają się macierzami obrotu i tworzą specjalną grupę obrotów. SO(3).
Specjalna grupa euklidesowa.
Wprowadzając do przestrzeni euklidesowej tzw. współrzedne jednorodne pozwalające opisać punkt o współrzędnych x =(x1,x2,x3)T układem liczb (x1,x2,x2,1)T, można przedstawić przemieszczenie ciała sztywnego przy pomocy macierz rozmiaru 4x4 postaci: ![]()
. Wówczas:
![]()
Do interpretacji tej transformacji należy rozważyć przemieszczenie ciała sztywnego w przestrzeni euklidesowej. Ponieważ podczas przemieszczania odległość między punktami ciała sztywnego nie ulega zmianie, jego ruch jest zdeterminowany przez ruch dowolnie wybranego punktu ciała. Wybierając taki punkt i umieszczając w nim prawoskrętny, kartezjański układ współrzędnych związany z ciałem sztywnym (układ ciała) oraz zakładając, że w chwili początkowej układ ciała i układ przestrzeni pokrywają się możemy stwierdzić, że po przemieszczeniu R i T wyznaczają położenie i orientację układu ciała względem układu przestrzeni. W konsekwencji, ruch ciała sztywnego w przestrzeni euklidesowej może być rozumiany jako gładkie przekształcenie czasu w grupę przesunięć R3 oraz w specjalną grupę obrotów SO(3), ![]()
które określa w każdej chwili położenie i orientację układu ciała względem układu przestrzeni. Obiekt SE(3) nazywamy specjalną grupą euklidesową i stanowi ona przestrzeń konfiguracyjną ciała sztywnego. Ponadto elementy tej grupy są reprezentowane przy pomocy macierzowej reprezentacji: S =![]()
. dimSE(3) = 6.
Prędkość kątowa ciała sztywnego w przestrzeni i w ciele.
W celu wprowadzenia pojęcia prędkości ruchu ciała sztywnego dla ruchu ![]()
obliczamy pochodną względem czasu ![]()
W ten sposób definiujemy dwa rodzaje prędkości ciała sztywnego: 1.prędkość w układzie przestrzeni: ![]()
2.prędkość w układzie ciała: ![]()
. W powyższych wyrażeniach ![]()
definiujemy jako prędkość kątową w układzie przestrzeni, ![]()
jest prędkością kątową w układzie ciała. Z ortogonalności macierzy obrotu wynika, że każda z macierzy ΩS, Ωb jest skośnie symetryczna rozmiaru 3x3, a zatem zdeterminowana przez wektory prędkości kątowej w układzie przestrzeni ωS i w układzie ciała ωb. Związek między macierzowymi a wektorowymi prędkościami kątowymi jest opisany przy pomocy odwzorowania zdefiniowanego formułą: ![]()
. To odwzorowanie jest wzajemnie jednoznaczne i określa wektorową reprezentację prędkości w układzie przestrzeni i w układzie ciała: ΩS=[ωS], ΩS=[ωb]. Ponadto, dla każdego wektora ![]()
jest spełniona zależność: ![]()
.
Związek między obydwiema prędkościami można wyrazić formułą: ![]()
, zatem:![]()
.
Parametryzacje grupy obrotów.
Elementarne obroty i przesunięcia.
Dla: ![]()
gdzie: ![]()
elementarne obroty i przesunięcia można ogólnie zdefiniować jako: ![]()
, ![]()
.
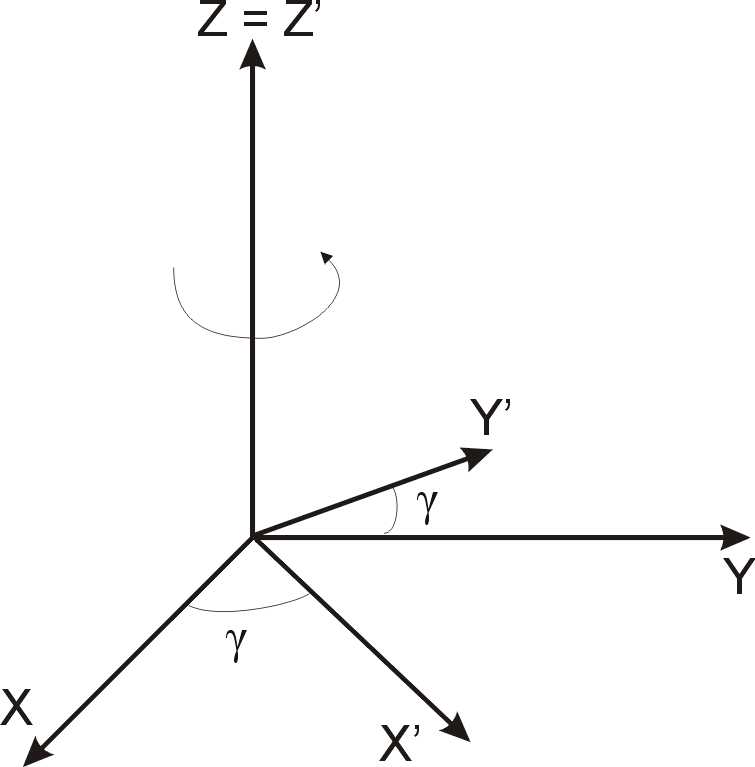
Przesunięcie dla poszczególnych osi definiujemy następująco: ![]()
- wzdłuż osi x o a,
![]()
![]()
Obroty dla poszczególnych osi definiujemy następująco:
- rotacja wokół osi z o kąt γ:
![]()
![]()
![]()
. Elementarne obroty i przesunięcia posiadają następujące właściwości: 1.Składanie przesunięć elementarnych jest przemienne. 2,Składanie obrotów elementarnych jest przemienne. 3.Składanie obrotów i przesunięć względem tej samej osi jest przemienne.
Kinematyka manipulatora: algorytm Denavita-Hartenberga.
Powszechnie przyjęty w robotyce sposób reprezentowania kinematyki manipulatora pochodzi od Denavita i Hartenberga. Algorytm ich konstrukcji polega na związaniu z każdym przegubem manipulatora lokalnego układu współrzędnych, a następnie określeniu ciągu transformacji sąsiednich układów współrzędnych, i prowadzi do wyliczenia kinematyki manipulatora jako złożenia tych transformacji.
Rozpatrując manipulator złożony z n ramion połączonych za pośrednictwem n przegubów, gdzie układ (X0, Y0, Z-0) jest związany z jego początkiem, zaś układ (Xn, Yn, Z-n) z jego efektorem, zaś qi oznacza kąt obrotu lub przesunięcie w i-tym przegubie algorytm Denavita-Hartenberga składa się z następujących kroków: 1.Z każdym przegubem wiążemy układ współrzędnych, tak żeby ruch w przegubie zachodził względem osi Z; 2. Układ (X0, Y0, Z-0) i (Xn, Yn, Z-n) umieszczamy orbitalnie; 3.Załóżmy, że znamy położenie układu (Xi-1, Y i-1, Z- i-1). Konstruujemy normalna do osi Zi-1i Zi. Początek układu (Xi, Yi, Z-i) umieszczamy na przecięciu normalnej z osią Zi. Oś Xi biegnie wzdłuż normalnej. Oś Yi dopełnia. Ponadto: -jeżeli Zi-1 || Zi to wybieramy normalną przechodzącą przez środek przegubu i+1; -jeżeli Zi-1 = Zi to postępujemy zgodnie „ze zdrowym rozsądkiem”; -jeżeli Zi-1 i Zi przecinają się, to poczatek układu (Xi, Yi, Z-i) umieszczamy w punkcie przecięcia, a Xi = Zi-1 x Zi.
4.Wyznaczamy przemieszczenie (Xi-1, Y i-1, Z- i-1). → (Xi, Yi, Z-i) jako złożenie elementarnych przesunięć i obrotów: ![]()
5.Definiujemy kinematykę manipulatora jako złożenie przemieszczeń ![]()
: ![]()
.
Odwrotne zadanie kinematyki manipulatora.
Odwrotnym zadaniem kinematyki nazywamy zadanie polegające na wyznaczeniu ruchu przegubów manipulatora zapewniającego wykonanie określonego ruchu efektora na przestrzeni zadaniowej. Zadanie formułuje się w następujący sposób: Mając daną trajektorię ruchu yd w przestrzeni zadaniowej i kinematykę ![]()
, wyznaczyć odpowiadająca jej trajektorię ruchu przegubów qd taką że: ![]()
. Z matematycznego punktu widzenia, odwrotne zadanie kinematyki polega na rozwiązaniu układu równań nieliniowych zadanych powyższą nierównością ze względu na wektor współrzędnych przegubowych qd(t). Jeżeli: 1.m>n to układ ten nie ma rozwiązania; 2.jeżeli n=m to układ posiada skończoną liczbę rozwiązań; 3.jezeli m<n to układ posiada nieskończoną liczbę rozwiązań. Układ ten można rozwiązać stosując metody analityczne lub numeryczne.
Jakobian analityczny.
Jakobinem analitycznym manipulatora nazywamy macierz Jacobiego: ![]()
reprezentacji kinematyki manipulatora we współrzędnych: k Rn → Rm, y=k(q) Jakobian analityczny można traktować jako przekształcenie prędkości zmian współrzędnych przegubowych w prędkość zmian współrzędnych zadaniowych, przy zadanej konfiguracji manipulatora, ![]()
. Postać jakobianu analitycznego zależy od wyboru układu współrzędnych (parametryzacji) dokonanego w celu zdefiniowania odwzorowania k.
Jakobian manipulatora.
Jakobian manipulatora jest to macierz przekształcenia prędkości ruchu w przegubach w prędkość liniową i prędkość kątową w przestrzeni efektora względem układu podstawowego tj.: ![]()
.
Rozpatrując manipulator złożony z n ramion połączonych za pośrednictwem n przegubów, gdzie układ (X0, Y0, Z-0) jest związany z jego początkiem, zaś układ (Xn, Yn, Z-n) z jego efektorem, zaś qi oznacza kąt obrotu lub przesunięcie w i-tym przegubie, jakobian manipulatora wyraża się jako: ![]()
Zatem: ![]()
. Aby wyliczyć ![]()
zatrzymujemy qk dla k≠i (![]()
) i analizujemy ruch efektora będący efektem ruchu w i-tym przegubie dla ![]()
. Jeżeli i-ty przegub jest obrotowy, to: ![]()
. Jeżeli i-ty przegub jest przesuwny, to: ![]()
. Ponadto istnieje związek między jakobianem manipulatora a jakobianem analitycznym. Dla y=(kartezjańskie, KKM) mamy: ![]()
gdzie: ![]()
.
Algorytmy jakobianowe kinematyki odwrotnej.
Konfiguracje osobliwe manipulatora.
Konfiguracje, jakie przyjmuje manipulator w czasie ruchu dzielą się na dwie klasy: konfiguracje regularne (nieosobliwe) i konfiguracje osobliwe. Konfigurację q manipulatora, w której rząd jakobianu analitycznego Jα(q) o ramiarze mxn jest mniejszy od m (wymiaru przestrzeni zadaniowej) tj.:
Jα(q) < m nazywamy konfiguracją osobliwą. W konfiguracji osobliwej istnieją ruchy przegubów, które nie powodują ruchu efektora manipulatora. Oznacza to ż manipulator traci zręczność ruchu. Stopień utraty zręczności ruchu w konfiguracji osobliwej mierzy się liczbą zwaną korzędem tej konfiguracji: corank q = m - rank Jα(q). Ponadto w konfiguracji osobliwej istnieją siły działające na efektor, których zrównoważenie nie wymaga siły w przegubach.
Elipsoida manipulowalności.
Rozważmy jakobian analityczny ![]()
. Zdefiniujmy sferę jednostkową w przestrzeni prędkości przegubowych ![]()
i wyznaczmy jej obraz w przestrzeni prędkości zadaniowych. W wyniku otrzymujemy elipsoidę ![]()
zwaną elipsoidą manipulowalności. Macierz ![]()
rozmiaru mxm nazywamy macierzą manipulowalności. Z definicji macierzy manipulowalności i twierdzenia Rayleigha-Tirza wynika następujące oszacowanie: ![]()
, gdzie ![]()
, ![]()
oznaczają, odpowiednio, najmniejsza i największą wartość własną macierzy M(q). W konsekwencji elipsoida zawiera się w pierścieniu sferycznym ograniczonym dwiema sferami: ![]()
oraz ![]()
o promieniach ![]()
,![]()
. Elipsoida manipulowalności obrazuje zdolności manipulacyjne manipulatora zwane zręcznością manipulatora. Przykładem miary liczbowej tej zdolności w danej konfiguracji jest objętość elipsoidy manipulowalności: ![]()
, gdzie funkcja m(q) nazywa się funkcją manipulowalności manipulatora. Własnością manipulowalności jest fakt, że w konfiguracjach osobliwych maleje do zera.
Rysunek przedstawia przykładową elipsoidę manipulowalności dla manipulatora typu podwójne wahadło oraz wpływ odległości od konfiguracji osobliwej na kształt elipsoidy.
Dynamika manipulatora sztywnego.
Energia kinetyczna i potencjalna manipulatora sztywnego o n stopniach swobody składa się z energii kinetycznej i energii potencjalnej każdego z ramion manipulatora wraz z jego układem napędowym.
Rozważmy manipulator przedstawiony na rysunku poniżej:
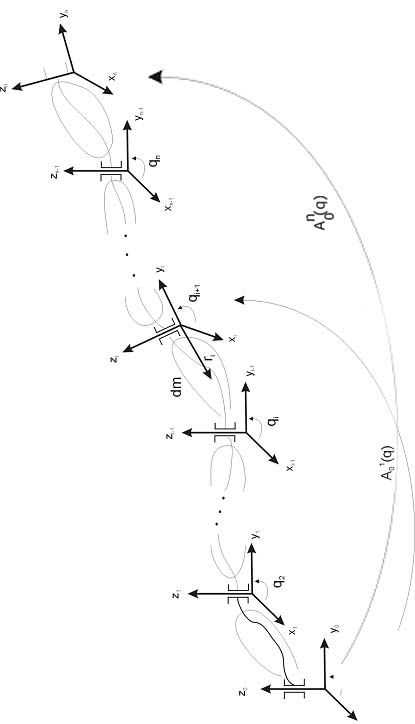
Rozważmy najpierw energię kinetyczna elementu masy dm ramienia o numerze i, którego położenie względem układu XiYiZi związanego z tym ramieniem jest określone przy pomocy współrzędnych jednorodnych ri=(xi,yi,zi,1)T. Zakładając, że transformacja kinematyczna: ![]()
, gdzie qi=(q1,...,qi)T, układu podstawowego X0Y0Z0 w układ XiYiZi jest znana obliczmy współrzędne elementu dm w układzie podstawowym jako ![]()
. Prędkość elementu dm względem układu podstawowego wynosi ![]()
. W konsekwencji, energia kinetyczna elementu dm i-tego ramienia: ![]()
Całkując energie kinetyczne wszystkich elementów ramienia nr i, wyliczamy energię kinetyczną ramienia: ![]()
![]()
gdzie 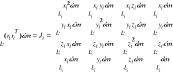
jest macierzą bezwładności i-tego ogniwa. Sumaryczna energia kinetyczna wszystkich ramion i układów napędowych manipulatora sztywnego jest opisana formuła: ![]()
![]()
,gdzie:![]()
gdzie: ![]()
oznacza funkcję zwaną deltą Kroneckera, określaną formułą: ![]()
. Energia potencjalna manipulatora pochodzi od oddziaływania pola grawitacyjnego Ziemi. W celu obliczenia tej energii dla i-tego ramienia można je potraktować jako masę punktową mi skupioną w środku masy ramienia. Zakładając, że Ri oznacza współrzędne jednorodne środka masy w układzie XiYiZi, obliczamy energię potencjalną i-tego ramienia jako: ![]()
jest wektorem przyśpieszenia ziemskiego w układzie podstawowym. Całkowita energia potencjalna manipulatora: ![]()
. Forma energii kinetycznej definiuje dwa pierwsze elementy modelu dynamiki (macierz inercji Q(q) i macierz sił odśrodkowych i sił Coriolisa ![]()
), natomiast gradient energii potencjalnej ![]()
wyznacza wektor sił grawitacji D(q). Ponadto występuje składni niepotencjalny ![]()
. Jeżeli składnik ten nie występuje, równania dynamiki manipulatora sztywnego mają postać: ![]()
gdzie u to wektor sterowania.
Dynamika manipulatora o elastycznych przegubach.
Dynamika manipulatora o elastycznych ramionach.
Zadanie śledzenia: metoda obliczanego momentu.
Ograniczenia holonomiczne i nieholonomiczne.
Załóżmy, że mamy dany pewien układ robotyczny opisany współrzędnymi uogólnionymi q=(q1,q2,...,qN)T należącymi do RN, oraz, że ruch układu jest opisany gładkim przekształceniem t →q(t). Oznaczmy przez ![]()
prędkości uogólnione układu. Wzajemne związki między elementami układu, a także między układem a jego otoczeniem, będziemy reprezentować w formie ograniczeń konfiguracyjnych: f(q)=(f1(q),f2(q),...,fk(q))T=0 oraz ograniczeń fazowych: ![]()
. Obecność ograniczeń fazowych może, ale nie musi, prowadzić do dalszego ograniczenia dopuszczalnych konfiguracji układu. Zależy to od własności ograniczeń fazowych zwanej holonomicznością. Ograniczenia fazowe nazywamy holonomicznymi, jeżeli jest możliwe ich scałkowanie i zastąpienie ograniczeniami postaci f(q)=(f1(q),f2(q),...,fk(q))T=0. Zatem w przypadku ograniczeń holonomicznych istnieje odwzorowanie h(q) = (h1(q),h2(q),...,hk(q))T, takie że ![]()
jest równoważne warunkowi h(q)=0. Ponadto ograniczenia ![]()
są holonomiczne jeżeli ![]()
pełnego rzędu i ![]()
, taka że ![]()
. Wówczas: ![]()
. Holonomiczne ograniczenia fazowe można dołączyć do ograniczeń konfiguracyjnych. Inaczej jest w przypadku ograniczeń nieholonomicznych. Nieholonomiczność ograniczeń ![]()
oznacza, że scałkowanie tego systemu nie jest możliwe, a obecność tych ograniczeń nie zmniejsza osiągalności konfiguracji w obrębie przestrzeni konfiguracyjnej. Utrudnieniu może ulec natomiast sposób osiągania pewnych konfiguracji. Ponadto jeżeli przez Dp oznaczymy dystrybucje układu, to jeżeli ![]()
gdzie ![]()
to ograniczenia ![]()
są nieholonomiczne.
Kinematyka robota mobilnego.
Kinematyka robota mobilnego określonego na uniwersum fazowym R2N, podlegającego l niezależnym ograniczeniom fazowym typu Pfaffa ![]()
jest zdefiniowana za pośrednictwem bezdryfowego układu sterowania ![]()
. Przy założeniu, że układ robotyczny nie podlega ograniczeniom konfiguracyjnym (k=0) wymiar przestrzeni stanu tego układu wynosi n=N. Macierz G(q)=[g1(q),g2(q),...,gn-1(q)], której kolumny rozpinają przestrzeń zerową macierzy A(q) jest rozmiaru nxm, gdzie m=n-l. Ponadto wektor ![]()
reprezentuje część składowych wektora prędkości ![]()
Mała flag układu, wektor wzrostu i stopień nieholonomiczności.
Nich G(q)=[g1(q),g2(q),...,gn-1(q)] będzie macierz, której kolumnami są wektory rozpinające przestrzeń linową Ker A(q) w konfiguracji q. Z niezależności ograniczeń fazowych wynika, że w każdym punkcie rząd G(q) jest pełny, rank G(q)=n-l=m, oraz że własność ![]()
jest równoważna istnieniu wektora ![]()
, takiego że ![]()
. Dystrybucją nazywamy obiekt geometryczny ![]()
wyznaczony w uniwersum fazowym przez pola wektorowe g1,g2,...,gm. Elementami dystrybucji są kombinacje pól g1,g2,...,gm mnożone przez funkcje gładkie.
Małą flagą dystrybucji nazywamy ciąg dystrybucji ![]()
. Jest ona generowana na podstawie rekurencyjnego wzoru: ![]()
dla i=0,1,... gdzie [D0,Di] jest operacją „mnożenia” zwaną nawiasem Liego i definiowaną następująco: ![]()
.
Zdefiniujmy ciąg (r0(q), r1(q),..., rP(q)) gdzie: ![]()
. Ciąg ten nazywamy wektorem wzrostu dystrybucji D0 w punkcie q. Jeżeli w każdym punkcie wektor wzrostu jest taki sam to flagę ![]()
nazywamy regularną.
Jeżeli istnieje granica ciągu ![]()
to najmniejsze p, przy którym ![]()
nazywa się stopniem nieholonomiczności układu w punkcie q.
Dynamika robota mobilnego.
Załóżmy, że mamy daną kinematykę mobilnego układu robotycznego podlegającego l niezależnym ograniczeniom fazowym typu Pfaffa, zdefiniowaną za pośrednictwem bezdryfowego układu sterowania ![]()
Aby otrzymać model dynamiki układu różniczkujemy tą kinematykę względem czasu: ![]()
i korzystamy z Zasady d'Alemberta, w myśl której siły uogólnione F zapewniające spełnienie ograniczeń fazowych nie wykonują pracy na dopuszczalnych przemieszczeniach. Z Zasady d'Alemberta wynika równość ![]()
, która wobec założonej niezależności ograniczeń fazowych prowadzi do wniosku, że istnieje wektor mnożników Lagrange'a ![]()
. Uwzględniając tą zależność w ogólnej postaci równań dynamiki układu robotycznego ![]()
oraz przy założeniu, że oddziaływania sterujące wpływają na m stopni swobody układu za pośrednictwem pewnej macierzy sterowań B(q), równania dynamiki mobilnego układu robotycznego z ograniczeniami nieholonomicznymi można zapisać w postaci: ![]()
. Macierz sterowań B(q) ma rozmiar nxm i składa się z elementów bij(q), takich że: ![]()
. W celu wyeliminowania mnożników λ korzystamy z własności: ![]()
. Ostatecznie równanie dynamik mobilnego układu robotycznego z ograniczeniami nieholonomicznymi przyjmuje postać: ![]()
.
![]()
Podstawy robotyki, III r. AiR lato 2007
1. Ruch ciała sztywnego w przestrzeni euklidesowej.
2. Specjalna grupa euklidesowa.
3. Prędkość kątowa ciała sztywnego w przestrzeni i w ciele.
4. Parametryzacje grupy obrotów.
5. Elementarne obroty i przesunięcia.
6. Kinematyka manipulatora: algorytm Deravita - Hartenberga.
7. Odwrotne zadanie kinematyki manipulatora.
8. Jakobian analityczny.
9. Jakobian manipulatora.
10. Algorytmy jakobianowe kinematyki odwrotnej.
11. Konfiguracje osobliwe manipulatora.
12. Elipsoida manipulowalności.
13. Dynamika manipulatora sztywnego.
14. Dynamika manipulatora o elastycznych przegubach.
15. Dynamika manipulatora o elastycznych ramionach.
16. Zadanie śledzenia: metoda obliczania momentu.
17. Ograniczenia holonomiczne i nieholonomiczne.
18. Kinematyka robota mobilnego.
19. Mała flaga układu, wektor wzrostu i stopień nieholonomiczności.
20. Dynamika robota mobilnego.
Literatura:
1. K. Tchoń et al.: manipulatory i roboty mobilne. Akademicka Oficyna Wydawnicza, W-wa, 2000.
2. M. W. Spong, M. Vidyasgar: Dynamika i sterowanie manipluatorow, WNT, W-wa, 1997.
3. J. J. Craig: Wprowadzenie do robotyki, WNT, W-wa, 1992
Poniżej jest opracowane 15 zagadnień z powyższej listy. Pytania opracowałem na podstawie książki prof. Tchonia „Manipulatory i Roboty Mobilne - Modele, planowanie ruchu, sterowanie” + notatki z wykładu. Pozostałe pytania zostawiam wam do opracowania, jest ich tylko 5!, więc niech to będzie wasz wkład w rozwój zasobów naszego portalu :]
Jeśli znajdziecie jakiś błędu to zróbcie z nimi porządek i uaktualnijcie ten plik w dziale downoload.
Na egzaminie trzeba było opisać dwa zagadnienia z powyższej listy.
.
Wyszukiwarka
Podobne podstrony:
SPRAWOZDANIE PARAMETRY, PWr, Automatyka i Robotyka, II semestr, Miernictwo 2, Laboratorium
L.2 Zasady drgania, PWr, Automatyka i Robotyka, II semestr, Fizyka 1.1A Radosz, Ćwiczenia
Zagadnienia na egzamin, PWR - Automatyka i Robotyka W10, Semestr 1, air
sciagaCAM - odlewnictwo, PWR - Automatyka i Robotyka W10, semestr 4, Obróbka bezubytkowa1, Odlewnict
Odlewnictwo sciaga, PWR - Automatyka i Robotyka W10, semestr 4, Obróbka bezubytkowa1, ODLEDNICTWO1,
wynikiI, PWR - Automatyka i Robotyka W10, Semestr 1, air
Odlewnictwo Janus Zestaw1, PWR - Automatyka i Robotyka W10, semestr 4, Obróbka bezubytkowa1, Odlewni
sylabus mikroekonomia, PWR - Automatyka i Robotyka W10, Semestr 1, Mikroekonomia
Wyklad10ALG2001, PWR - Automatyka i Robotyka W10, Semestr 1, air
opr zadan, PWR - Automatyka i Robotyka W10, Semestr 1, air, materialy, Nowy folder
Odlewnictwo wyk1, PWR - Automatyka i Robotyka W10, semestr 4, Obróbka bezubytkowa1, ODLEDNICTWO1, od
aspec wyklad234, PWR - Automatyka i Robotyka W10, semestr 4, Podstawy automatyki, Podstawy Automatyk
lista 1 i 2, PWR - Automatyka i Robotyka W10, Semestr 1, air
Półprzewodniki ZENER SPRAWKO, PWr, Automatyka i Robotyka, II semestr, Fizyka 3.3, Laboratoria
Regulatory, PWR - Automatyka i Robotyka W10, semestr 4, Podstawy automatyki
Przyklad Test, PWR, Automatyka i Robotyka (AIR), Semestr II, Fizyka 3.3, Wykład
51-60, PWR - Automatyka i Robotyka W10, Semestr 1, air, Fizyka 1.2, Zagadnienia Egzmin Popko
!!! Zagadnienia, Automatyka i robotyka air pwr, VI SEMESTR, Syst. monit. i diagn. w przem, Opracowan
Pytanie nr 9, Automatyka i robotyka air pwr, VI SEMESTR, Syst. monit. i diagn. w przem, Opracowane z
więcej podobnych podstron