Numer ćwiczenia 105	Data 18.03.2008	Bucholc Tytus Burdach Hubert	Wydział Elektryczny Informatyka	Semestr II	Grupa 5
prowadzący: dr Aleksander Skibiński			Przygotowanie:	Wykonanie:	Ocena ostat.:

Wyznaczanie współczynnika rozszerzalności liniowej ciał stałych

1. Wstęp teoretyczny:

Zmianie temperatury ciała towarzyszy na ogół zmiana jego wymiarów liniowych, a więc i zmiana objętości. Elementarny przyrost temperatury dt ciała, którego długość całkowita wynosi l, powoduje przyrost długości dl określony wzorem:

(1)

Współczynnik α nazywamy współczynnikiem rozszerzalności liniowej. Jego wartość liczbowa równa jest względnemu przyrostowi długości dl/l spowodowanemu zmianą temperatury o 1^oC i zależy od rodzaju ciała a także od temperatury. W związku z zależnością współczynnika α od temperatury, długość ciała jest na ogół nieliniową funkcją temperatury. Dla niewielkich zmian temperatury w przybliżeniu można przyjąć, że współczynnik α jest stały (mówimy wówczas o średnim współczynniku rozszerzalności liniowej), a długość wzrasta wprost proporcjonalnie do temperatury. W tej sytuacji odpowiednikiem wzoru (1) jest następujący wzór:

(2)

Przyczyny zjawiska rozszerzalności cieplnej należy szukać w strukturze mikroskopowej ciał. Ciała stałe np. zbudowane są z atomów (jonów) rozłożonych regularnie w przestrzeni i tworzących sieć krystaliczną. Atomy są wzajemnie ze sobą powiązane siłami pochodzenia elektrycznego, co uniemożliwia im trwałą zmianę położenia. Dostarczona do kryształu energia cieplna wywołuje drgania atomów wokół położeń równowagi. Amplituda tych drgań rośnie wraz z temperaturą. Częstotliwość drgań cieplnych atomów sięga 10¹³ Hz.

W tej sytuacji pojęcie odległości międzyatomowej ma sens tylko jako odległość między środkami drgań sąsiednich atomów.

Energia potencjalna dwóch oddziałujących ze sobą atomów jako funkcja odległości między atomami wyrażona jest krzywą przedstawioną na rys. 1. Gdyby energia kinetyczna atomów była równa zeru, znajdowały by się one w odległości r_o od siebie, dla której to odległości energia potencjalna posiada minimum. W rzeczywistości atomy wykonują drgania wokół położeń równowagi, tzn. mają określoną energię kinetyczną, która wzrasta wraz z temperaturą. W temperaturze T₁ odległość między atomami zmienia się od wartości a₁ do wartości b₁.

Rysunek 1. Energia potencjalna dwóch atomów jako funkcja ich wzajemnej odległości.

Wskutek asymetrii krzywej potencjalnej średnie położenie drgającej cząsteczki nie będzie się pokrywać z wartością r_o, lecz przesunie się w prawo osiągając wartość r₁.

Przy podwyższeniu temperatury do T₂ atom przejdzie na wyższy poziom energetyczny E_k2 - jego ruch drgający będzie się odbywał między punktami a₂ i b₂, a średnie położenie osiągnie wartość r₂.

Z powyższego opisu wynika, że wraz ze wzrostem temperatury rośnie nie tylko amplituda drgań atomów, lecz także ich średnia wzajemna odległość, co makroskopowo objawia się jako rozszerzalność cieplna.

Wartość współczynnika rozszerzalności liniowej w ciałach polikrystalicznych nie zależy od kierunku, natomiast w monokryształach (ciała anizotropowe) zależność od kierunku jest wyraźna - zamiast jednego występują tutaj trzy główne współczynniki rozszerzalności liniowej określone dla trzech głównych osi krystalograficznych kryształu.

2. Wykorzystane zależności:

Podczas przeprowadzania ćwiczenia wykorzystaliśmy następujące zależności:

1. zależność przyrostu długości ciała w zależności od jego temperatury:

Skąd można wyprowadzić bezpośredni wzór na współczynnik rozszerzalności liniowej:

2. Błąd współczynnika rozszerzalności obliczamy z różniczki zupełnej:

3. Wzór na odchylenie standardowe:

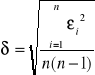
3. Tabela pomiarów i obliczenia:

- Mosiądz l₀ = 0.77 m Δ(ΔT) = ± 1⁰C Δ(Δl) = ± 10^-5 m Δl₀ = ± 0,05mm

Temp	ΔT	Δl	l	αśr	Δαśr
^0C ± 1	^0C ± 1	m ± 0.00001	m ± 0.00001	[1/^0C]	[1/^0C]
20	0	0	0.77000	-	-
25	5	0.00008	0.77008	2,07792E-05	6,7546E-06
30	10	0.00015	0.77015	1,94805E-05	3,24802E-06
35	15	0.00022	0.77022	1,90476E-05	2,13688E-06
40	20	0.00029	0.77029	1,88312E-05	1,59213E-06
45	25	0.00036	0.77036	1,87013E-05	1,26875E-06
50	30	0.00043	0.77043	1,86147E-05	1,0546E-06
55	35	0.00050	0.77050	1,85529E-05	0,90234E-06
60	40	0.00057	0.77057	1,85065E-05	0,78854E-06
55	35	0.00050	0.77050	1,85529E-05	0,90234E-06
50	30	0.00044	0.77044	1,90476E-05	1,06906E-06
45	25	0.00036	0.77036	1,87013E-05	1,26875E-06
40	20	0.00029	0.77029	1,88312E-05	1,59213E-06
35	15	0.00022	0.77022	1,90476E-05	2,13688E-06
30	10	0.00016	0.77016	2,07792E-05	3,37797E-06

Średnia arytmetyczna z α_śr α_śr = 1,91053E-05

Średnia arytmetyczna z Δα_śr Δα_śr = 0,20066E-05

Odchylenie standardowe α_śr od α_śr δ = 0,02022E-05

Błąd całkowity Δα_śr^c = Δα_śr + 3δ ≈ 0,26132E-05

Uzyskana z doświadczenia wartość średnia współczynnika rozszerzalności liniowej dla mosiądzu wynosi:

α_śr = (1,91 ± 0,26) 10^-s 1/⁰C

- Stal l₀ = 0.77 m Δ(ΔT) = ± 1⁰C Δ(Δl) = ± 10^-5 m Δl₀ = ± 0,05mm

Temp	ΔT	Δl	l	αśr	Δαśr
^0C ± 1	^0C ± 1	m ± 0.00001	m ± 0.00001	[1/^0C]	[1/^0C]
20	0	0	0.77000	-	-
25	5	0.00002	0.77002	5,19481E-06	3,6367E-06
30	10	0.00005	0.77005	6,49351E-06	1,94847E-06
35	15	0.00007	0.77007	6,06061E-06	1,27023E-06
40	20	0.00011	0.77011	7,14286E-06	1,00696E-06
45	25	0.00014	0.77014	7,27273E-06	8,10862E-07
50	30	0.00018	0.77018	7,79221E-06	6,93147E-07
55	35	0.00021	0.77021	7,79221E-06	5,94198E-07
60	40	0.00025	0.77025	8,11688E-06	5,28124E-07
55	35	0.00022	0.77022	8,16327E-06	6,04824E-07
50	30	0.00018	0.77018	7,79221E-06	6,93147E-07
45	25	0.00015	0.77015	7,79221E-06	8,31675E-07
40	20	0.00012	0.77012	7,79221E-06	1,03947E-06
35	15	0.00009	0.77009	7,79221E-06	1,38579E-06
30	10	0.00006	0.77006	7,79221E-06	2,07843E-06

Średnia arytmetyczna z α_śr α_śr = 7,35644E-06

Średnia arytmetyczna z Δα_śr Δα_śr = 1,223E-06

Odchylenie standardowe α_śr od α_śr δ = 2,30951E-07

Błąd całkowity Δα_śr^c = Δα_śr + 3δ ≈ 1,91586E-06

Uzyskana z doświadczenia wartość średnia współczynnika rozszerzalności liniowej dla stali wynosi:

α_śr = (0,74 ± 0,2) 10^-s 1/⁰C

4. Wykresy:

5. Wnioski:

Zestawienie wyników doświadczenia wypadło następująco :

	TABLICE	DOŚWIADCZENIE
mosiądz	α = (1.88 ÷ 1.93) * 10^-5 [1/^0C]	α = (1.91 ± 0.26) * 10^-5 [1/^0C]
stal	α = 1.2 * 10^-5 [1/^0C]	α = (0.74 ± 0.2) * 10^-5 [1/^0C]

Jak widać otrzymane w wyniku doświadczenia wartości są zbliżone do danych tablicowych. Zaistniałe różnice mogą być przyczyną błędów odczytu i nierównomierną temperaturą na całej długości prętów. Uważam, że cel ćwiczenia został osiągnięty, a wyniki są zadowalające.

1

---