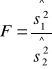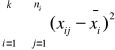Statystyka matematyczna modele i zadania, Jerzy Greń, W-wa 1976, PWN

parametr-charakteryzuje rozkład

Estymator nieobciążony - estymator Z spełniający równość E(Z)= θ, oznaczającą, że estymator Z szacuje parametr θ bez błędu systematycznego

Estymator efektywny - estymator Z o możliwie małej wariancji D²(Z). Stosowanie estymatora efektywnego oznacza popełnianie małego błędu przeciętnego szacunku D(Z)

Estymator zgodny - estymator Z parametru θ spełniający warunek lim P{|Z_n-θ|<ε}=1, tzn. estymator, który jest stochastycznie zbieżny do parametru θ, czyli jest to estymator podlegający działaniu prawa wielkich liczb. Gdy używa się estymatora zgodnego parametru θ, to stosowanie większych prób poprawia dokładność szacunku tego parametru

Estymator wystarczający (dostateczny) - estymator Z skupiający w sobie wszystkie informacje o parametrze θ zawarte w próbie losowej

estymacja przedziałowa - estymacja parametru θ polegająca na budowaniu tzw. przedziału ufności dla tego parametru

przedział ufności - losowy przedział wyznaczony za pomocą rozkładu estymatora, a mający tą własność, że z dużym, z góry danym prawdopodobieństwem, pokrywa wartość szacowanego parametru θ. Zapisujemy go zwykle w postaci P(a<θ<b)=1-α, gdzie a i b noszą nazwę dolnej i górnej granicy (końca) przedziału ufności, a prawdopodobieństwo 1-α jest dane z góry.

Współczynnik ufności - prawdopodobieństwo 1-α występujące po prawej stronie wzoru na przedział ufności, a oznaczające prawdopodobieństwo, z jakim parametr θ jest pokryty tym przedziałem.

Hipoteza statystyczna - jakiekolwiek przypuszczenie dotyczące rozkładu populacji generalnej

Hipoteza parametryczna - hipoteza precyzująca wartość parametru w rozkładzie populacji generalnej znanego typu

Hipoteza nieparametryczna - hipoteza statystyczna precyzująca typ rozkładu populacji generalnej

Hipoteza zerowa - podstawowa hipoteza statystyczna sprawdzana danym testem. Oznacza się ją H₀

Hipoteza alternatywna - hipoteza statystyczna konkurencyjna w stosunku do hipotezy zerowej w tym sensie, że jeżeli odrzuca się hipotezę zerową, to przyjmuje się hipotezę alternatywną. Oznacza się ją H₁

Błąd pierwszego rodzaju - polega na odrzuceniu testowanej hipotezy prawdziwej

Błąd drugiego rodzaju - polega na przyjęciu testowanej hipotezy fałszywej

Poziom istotności - prawdopodobieństwo popełnienia błędu pierwszego rodzaju w postępowaniu testującym hipotezę. Poziom istotności oznacza się symbolem α i obiera go z góry, zwykłe jako małe prawdopodobieństwo, 0,1, 0,05, 0,01, 0,001. Odrzucenie sprawdzanej hipotezy na poziomie istotności np. α=0,05 oznacza, że ryzyko popełnienia błędu pierwszego rodzaju przy tej decyzji wynosi 5%.

Test statystyczny - reguła postępowania, która na podstawie wyników próby ma doprowadzić do decyzji przyjęcia lub odrzucenia postawionej hipotezy statystycznej. Za pomocą testu weryfikujemy zatem hipotezę statystyczną.

Moc testu - prawdopodobieństwo podjęcia decyzji prawidłowej przy weryfikacji hipotezy statystycznej danym testem, a polegającej na odrzuceniu testowanej hipotezy fałszywej

Test istotności - test pozwalający na odrzucenie hipotezy z małym ryzykiem popełnienia błędu (mierzony poziomem istotności α). Ze względu na to, że w teście istotności uwzględnia się jedynie błąd pierwszego rodzaju, to w wyniku tego testu możliwa jest decyzja odrzucenia hipotezy zerowej lub nie ma podstaw do jej odrzucenia (co nie oznacza jej przyjęcia).

Obszar krytyczny testu - podzbiór przestrzeni próby o tej własności, że jeżeli otrzymamy w próbie punkt przestrzeni próby należący do tego podzbioru, to podejmuje się decyzję odrzucenia hipotezy zerowej. Obszar krytyczny testu dwustronny ma postać nierówności ≠. Obszar jednostronny ma postać nierówności < (lewostronny) lub > (prawostronny)

ESTYMACJA PRZEDZIAŁOWA PARAMETRÓW

Niemal wszystkie parametry szacowane w postaci przedziału mają jednakową regułę postępowania. Model I opiera się na założeniu, że populacja generalna ma rozkład normalny N(m, σ), gdzie m to średnia w populacji generalnej, a σ to znane odchylenie standardowe w populacji generalnej. Z populacji tej wylosowano próbę o liczebności n-elementów . Z tablic rozkładu normalnego dla danego współczynnika ufności 1-α odczytuje się wartość u_α . Model III stosuje te same wzory, z tym, że populacja może mieć rozkład normalny lub dowolny, ale nieznane jest odchylenie standardowe (lub wariancja σ²) z populacji generalnej, lecz próba musi być duża n>=30. Model II stosowany jest gdy próba losowa jest mała n<30. Dla n-1 stopni swobody oraz dla α odczytuje się z tablic rozkładu t-studenta współczynnik t_α.

Przedział ufności dla średniej.

średnia arytmetyczna z próby x ma wszystkie pożądane własności estymatorów: zgodność, nieobciążoność, efektywność, dostateczność.

Model I

populacja generalna o rozkładzie N(m,σ), wartość m jest nieznana, próba o liczebności n

Przedział ufności dla średniej m populacji otrzymuje się ze wzoru

P{x - u_α * σ/pierwiastek z n < m < x + u_α * σ/pierwiastek z n}=1-α

x-średnia arytmetyczna z próby

wartość u_α wyznacza się z tablicy (dystrybuanty) rozkładu normalnego dla 1-α w taki sposób, by spełniona była relacja P(-u_α < U < u_α )=1-α.

Dla najczęściej przyjmowanego współczynnika ufności 1-α=0,95 mamy u_α=1,96

Model II

populacja o rozkładzie normalnym N(m,σ) nieznana ani średnia m ani odchylenie standardowe σ. próba mała losowana niezależnie.

P{x-t_α * s/pierwiastek(n-1) < m < x+t_α * s/pierwiastek(n-1)}=1-α

lub wg wzoru równoważnego

P{x-t_α * sd/pierwiastek z n < m < x + t_α * sd/pierwiastek z n}=1-α

s=pierwiastek (1/n * ∑(x_i -x)²) dla i=1 do n) a sd=pierwiastek(1/(n-1) * ∑(x_i -x)²) dla i=1 do n}

σWartość t_α to wartość zmiennej t Studenta odczytaną z tablicy tego rozkładu dla n-1 stopni swobody, że dla 1-α spełniona jest relacja P(-t_α < t < t_α )=1-α

Model III

populacja generalna o rozkładzie normalnym N(m,σ) lub dowolnym innym o średniej m i skończonej wariancji σ² (nieznanej). populacja próbna o liczebności dużej n>30.

Dla szeregu rozdzielczego obliczamy średnią i odchylenie standardowe z środków przedziałów.

Gdy liczba r przedziałów klasowych jest mała, tzn. gdy długość h każdego przedziału jest duża, należy przed spierwiastkowaniem s² zastosować poprawkę na grupowanie, th.. odjąć od s² 1/12h²

P1

Wytrzymałość pewnego materiału budowlanego jest zmienna losową o rozkładzie N(m,σ). W celu oszacowania nieznanej średniej m wytrzymałości tego materiału dokonano pomiarów wytrzymałości dla n=5 wylosowanych niezależnie sztukach tego materiału. Wyniki pomiarów były następujące w kG/cm² : 20,4, 19,6, 22,1, 20,8, 21,1. Przyjmując współczynnik ufności 1-α=0,99 zbudować przedział ufności dla średniej wytrzymałości m tego materiału

x=20,8 kG/cm² s=0,82 kG/cm²

dla 1-α=0,99 oraz dla n-1=4 stopni swobody t_α =4,604

20,8-4,604* (0,82/pierw(4)) < m < 20,8 +4,604 * (0,82/pierw(4))

20,8-1,9 < m < 20,8 +1,9

skąd 18,9 < m < 22,7

Zatem przedział liczbowy o końcach 18,9 i 22,7 kG/cm² z ufnością 0,99 pokrywa nieznaną średnią wytrzymałość tego materiału. Do obliczeń inżynierskich należy wziąć pod uwagę także 18,9 kG/cm²

Z1

oszacować żywotność wyprodukowanej partii świetlówek.

Z2

Oszacować z ufnością 0,999 średnią ilość wydzielonej w doświadczeniu chemicznym substancji.

Z3

Oszacować średnią miesięczną kwotę wydatków studentów na rozrywki

Przedział ufności dla wskaźnika struktury

Dla cech jakościowych stosuje się następujące wzory

Podstawowym parametrem populacji szacowanym w tym badaniu jest frakcja elementów wyróżnionych w populacji, zwana wskaźnikiem struktury populacji. Wskaźnik struktury oznacza się przez p.

Frakcję p elementów wyróżnionych szacuje się z tych wzorów w oparciu o wyniki dużej próby (n >=100).

Model.

Populacja generalna o rozkładzie dwupunktowym z parametrem p. Elementy podzielone na dwie klasy, gdzie frakcja elementów wyróżnionych wynosi p i jest >0,05. Próba losowana niezależnie.

Przedział ufności dla p gdzie m - liczba elementów wyróżnionych w próbie

P{ m/n - u_α * pierwiastek ( (m/n * (1-m/n))/n) < p < m/n +u_α * pierwiastek ( (m/n * (1-m/n))/n)}=1-α

P1

Jaki procent pracujących mieszkańców Warszawy jada obiady w stołówkach pracowniczych. Pobrano w tym celu n=900 osób wylosowanych niezależnie do próby i znaleziono w tej próbie m=300 osób, które jedzą obiady w stołówkach. Przyjmując współczynnik ufności 1-α=0,95 zbudować przedział ufności dla procentu badanej kategorii pracujących.

m/n=300/900 = 1/3 = 0,333

człon pod pierwiastkiem = pierwiastek( (1/3 * 2/3)/900 = 0,016

z tablicy rozkładu normalnego N(0,1) dla 1-α=0,95 tzn. dla α=0,05 znajdujemy u_α =1,96.

0,333-1,96*0,016 < p < 0,333 + 1,96 *0,016 czyli 0,302 < p < 0,364

Z

Spośród skrzynek zmagazynowanej broni wylosowano do kontroli 240 skrzynek. Po otwarciu okazało się, że 18 skrzynek wykazuje obecność rdzy. Przyjmując współczynnik 0,999 ufności oszacować procent magazynowanych skrzynek z bronią dotknięta procesem korozyjnym.

Przedział ufności dla wariancji

Gdy populacja generalna ma rozkład normalny (lub zbliżony) to można zbudować przedział ufności dla wariancji σ² populacji. Budowę przedziału ufności dla wariancji opiera się zwykle na rozkładzie statystyki, będącej jej estymatorem.

estymator s² (z daszkiem) jest nieobciążonym estymatorem wariancji σ² (ale s² nim nie jest).

Gdy chodzi o przedział ufności to estymatory te są równoważne.

Estymatory s i s(daszek) są obciążonymi estymatorami odchylenia standardowego σ.

W zależności od tego czy próba jest mała czy duża, przedział ufności dla wariancji budujemy odpowiednio w oparciu bądź o dokładny rozkład statystyki s² (rozkład ² )

bądź też o jej rozkład graniczny (rozkład normalny)

Obliczając pierwiastek kwadratowy z otrzymanych końców przedziału ufności dla wariancji σ² otrzymujemy przedział ufności dla odchylenia standardowego σ.

W dużej próbie można podać od razu przedział ufności dla odchylenia standardowego σ, korzystając z faktu, że s ma rozkład asymptotyczny N(σ,σ/pierw(2n)).

Model I

populacja generalna ma rozkład normalny N(m,σ), o nieznanych obu parametrach. Z populacji tej wylosowano niezależnie do próby n elementów (n<30). Z próby oblicza się s² lub sd²

przedział ufności dla wariancji σ² populacji generalnie określony jest wzorem

P(ns² / c₂ < σ² < ns² / c₁ }=1-α

lub Pn-1)*sd² /c₂ < σ² < (n-1)*sd² / c₁ } 1-α

gdzie c1 i c2 SA wartościami zmiennej ² wyznaczonymi z tablicy rozkładu ² dla n-1 stopni swobody oraz współczynnika ufności 1-α tak by

P(² < c1)=1/2α oraz P(² >=c2)=1/2α

Ponieważ powszechnie używane tablice rozkładu ² podają prawdopodobieństwo P(² >=²_α } zatem dla określonego współczynnika ufności 1-α wartość c1 znajdujemy z tablic rozkładu ² dla prawdopodobieństwa 1-1/2α, natomiast c2 dla 1/2α.

Otrzymany przedział ufności nie jest symetryczny względem wartości s²

Model II

populacja generalna ma rozkład N(m,σ) lub zbliżony o obu nieznanych parametrach. Z populacji wylosowano niezależnie dużą liczbę elementów (N>=30). Z próby oblicza się s, wtedy przybliżony przedział ufności dla odchylenia standardowego σ populacji generalnej określony jest wzorem

P(s/(1+u_α /pierw(2n)) < σ < s/ (1- u_α /pierw(2n))}=1-α

P1.

Badając wytrzymałość elementu konstrukcyjnego dokonano n=4 niezależnych pomiarów wytrzymałości i otrzymano następujące wyniki (w kG/cm² ) : 120, 102, 135, 115. Należy zbudować przedział ufności dla wariancji σ2 wytrzymałości tego elementu dla 1-α=0,96

Przyjmujemy, że rozkład wytrzymałości jest zbliżony do normalnego, ze względu na małą próbę jest to model I

obliczamy ns²

∑x_i =472 ∑(x_i - x)² =558

x=118 ns² =558

Z tablicy rozkłady ² dla n-1=3 stopni swobody odczytujemy dla 1-1/2α=0,98 wartość c₁ =0,185 oraz dla 1/2α=0,02 wartość c₂ =9,837,

Przedział ufności:

558/9,837 < σ² < 558 / 0,185

czyli

56,7 < σ² < 3016

dla σ

7,5 < σ < 54,9

Z

W celu oszacowania dokładności pewnego przyrządu pomiarowego dokonano w nim 5niezależnych pomiarów długości pewnego odcinka i otrzymano następujące wyniki w mm: 15,15, 15,20, 15,04, 15,14, 15,22. Przyjmując współczynnik ufności 0,98, zbudować przedział ufności dla nieznanej wariancji pomiarów tym przyrządem.

Z

Wyznaczanie niezbędnej liczby pomiarów do próby

Szacując metodą przedziałową parametr θ populacji generalnej, budujemy dla niego przedział ufności w oparciu o rozkład estymatora, przy założeniu posiadanych wyników próby o ustalonej z góry liczebności n. Otrzymany przedział liczbowy ma pewną długość 2d i może okazać się, że d , która jest miarą maksymalnego błędu szacunku parametru, jest za duże.

Model I

Populacja generalna ma rozkład normalny N(m,σ) bądź zbliżony do normalnego. Wariancja z populacji σ² jest znana. Chcemy oszacować nieznaną średnią wartość m populacji na podstawie próby złożonej z n niezależnych pomiarów. Jeżeli żądamy, by przy ustalonym współczynniku ufności 1-α maksymalny błąd szacunku średniej m (tj. połowa długości przedziału ufności) nie przekroczył z góry danej liczby d, to niezbędną do uzyskania tego celu liczebność próby n oblicza się z wzoru

n = (u_α² σ² ) / d²

gdzie d to dopuszczalny maksymalny błąd szacunku średniej m

Model II

populacja generalna ma rozkład N(m, σ) Wariancja σ² jest nieznana, ale znana jest wartość statystyki sd² ( dla n-1) uzyskana z małej próby wstępnej o liczebności n₀ elementów.

n = (t_α² sd² ) / d²

t_α odczytana z tablicy t-Studenta dla n₀ -1 stopni swobody

Liczebność zaokrągalmy do 1 zawsze w górę.

Jeżeli liczebność właściwej próby spełnia nierówność n <=n₀ to liczebność n₀ próby wstępnej jest wystarczająca. Jeśli zaś nie, to należy doloswać do właściwej próby n-n₀ elementów.

Model III

populacja generalna ma rozkład dwupunktowy z parametrem p (p - frakcja elementów wyróznionych w populacji)

a) jeżeli znany jest spodziewany rząd wielkości szacowanej frakcji p to

n = (u_α ² pq)/d² q=1-p

b) jeżeli nie znamy rzędu wielkości szacowanego wskaźniki to przymujemy największą jego wartość tj. ¼

n = u_α ² /4d²

Jeżeli prawdziwa wartość p spełnia nierówność p≠ ½ to obliczona wielkość próby jest za duża.

P1

Należy oszacować średnią wartość masy pewnej substancji wydzielającej się w pewnym doświadczeniu chemicznym. Ile niezależnych doświadczeń należy przeprowadzić aby przy współczynniku ufności 0,95 oszacować metodą przedziałową tę średnią masę z błedem maksymalnym 0,01 g jeżeli próba wstępna 5 niezależnych doświadczeń dała wyniki: 2,10, 2,12, 2,12, 2,16, 2,10?

x=10,6/5 = 2,12

sd² =0,0024/4 =0,0006

t_α =2,776 (4 stopnie swobody, α=0,05)

n = (2,776² * 0,0006)/ (0,01)² = 7,73 * 6 ≅ 47

n=47>5=n₀

zatem należy jeszcze dokonać 42 dodatkowe pomiary masy

P2

Zbadać, ile należy wylosować studentów uczelni, do próby, by oszacować procent studentów tej uczelni palących papierosy z błędem maksymalnym 5%, przy współczynniku ufności 0,90. Przypuszcza się, że szacowany procent palących studentów jest rzędu 70%..

Z tablicy rozkładu normalnego dla 1-α=0,90 odczytujemy wartość u_α =1,64. Mamy d=0,05 oraz p=0,7, czyli q=0,3.

n = (1,64² 0,7*0,3)/0,05² = 5649/25 =225,96 ok. 226

gdyby nie był znany rząd wielkości, otrzymalibyśmy

n=1,64² / 4* 0,05² = 2,69 / 0,01 =269

Z.

Ile sztuk pewnego wyrobu należy pobrać do kontroli wagi, aby oszacować średnią wagę tego wyrobu z błedem maksymalnym 0,5dkg przy współczynniku ufności 0,99, jeżeli wiadomo, że wariancja wagi wynosi 1 dkg?

Z

Ile należy wylosować puszek konserwowych do badania jakości partii konserw, aby oszacować procent zepsutych konserw, który wynosi przypuszczalnie 10% z błędem maksymalnym 5%. Współczynnik ufności 0,90

Z

Ilu mieszkańców miasta należy wylosować, aby oszacować procent mieszkańców chorych na choroby reumatyczne, jeżeli nie chcemy się pomylić o więcej niż 5%

Z

Ile należałoby wykonać doświadczeń fizycznych aby oszacować z błędem maks. 8% nieznany procent doświadczeń, w którym powstaje efekt akustyczny (1-α=0,95)

Parametryczne testy istotności

Przyjęcie lub odrzucenie hipotezy statystycznej w teście statystycznym nie jest równoznaczne z logicznym udowodnieniem jej prawdziwości lub fałszywości. Należy bowiem pamiętać, że odrzucając sprawdzaną hipotezę kierujemy się jedynie tym, że dane liczbowe wynikające z badania rzeczywistości dają nam małą szanse prawdziwości tej hipotezy, nie zgadzają się z nią. Możliwe jednak, że jest na odwrót, tzn hipoteza jest prawdziwa, a tylko nasze dane liczbowe z próby są złe lub po prostu mało prawdopodobne przy tej hipotezie.

W ogólnej teorii weryfikacji hipotez statystycznych rozpatruje się różne rodzaje testów, np. testy najmocniejsze, nieobciążone itd. , lecz największe praktyczne znaczenie ma jeden typ testów, zwany testami istotności.

Testy istotności, to taki rodzaj testów, w których na podstawie wyników próby losowej podejmuje się jedynie decyzję odrzucenia hipotezy sprawdzanej lub stwierdzenia, że brak jest podstaw do jej odrzucenia. Nie podejmuje się natomiast w teście istotności decyzji o przyjęciu sprawdzanej hipotezy, gdyż bierze się pod uwagę jedynie błąd pierwszego rodzaju (prawdopodobieństwo to poziom istotności), a nie uwzględnia się konsekwencji popełnienia błędu drugiego rodzaju.

Mimo to, testy te są zupełnie wystarczające. Jest tak dlatego, że najczęściej hipotezę badawczą da się zamienić na odpowiednią odwrotną hipotezę statystyczną, której odrzucenia pragnie praktyk, a na przyjęciu której wcale mu nie zależy.

Ogólnie rzecz biorąc, statystyczne testy istotności powstają w taki sposób, że w zależności od postaci hipotezy zerowej buduje się pewną statystykę Z z wyników n-elementowej próby i wyznacza się rozkład tej statystyki przy założeniu prawdziwości hipotezy H₀ W rozkładzie tym wybiera się taki obszar Q wartości statystyki Z, by spełniona była równość

P{Z⊂Q}=α

gdzie α jest ustalonym z góry, dowolnie małym prawdopodobieństwem. Obszar Q nazywa się obszarem krytycznym testu, gdyż ilekroć wartość statystyki Z z próby znajdzie się w nim, to poedejmuje się decyzję odrzucenia hipotezy H₀ na korzyśc jej alternatywy H₁

Uzasadnienie:

Obszar krytyczny Q został tak dobrany, że przy prawdziwości hipotezy H₀ prawdopodobieństwo otrzymania z próby n-elementowej wartości statystyki Z należącej do tego obszaru jest znane i jest bardzo małą liczbą. Takie zdarzenie losowe nie powinno się więc zrealizować w jednym doświadczeniu. Jeżeli jednak zrealizowało się, to musiało mieć większe prawdopodobieństwo niż to wynika z założenia prawdziwości hipotezy H₀ więc skłonni jesteśmy uznać hipotezę za fałszywą i odrzucamy ją. Jeżeli natomiast wartość statystyki Z z próby znalazła się poza obszarem krytycznym, to prawdopodobieństwo tego zdarzenia, przy prawdziwości hipotezy zerowej jest równe 1-α, co jest bliskie 1. Zaszło więc zdarzenie, które powinno przy prawdziwości hipotezy zajść, bo miało duże prawdopodobieństwo, więc nie ma podstaw do odrzucenia hipotezy zerowej.

Odrzucenie sprawdzanej hipotezy zerowej na poziomie istotności np. 0,01 oznacza, że odrzucając tę hipotezę albo się nie mylimy (tzn. że hipoteza jest naprawdę fałszywa) albo popełniamy błąd pierwszego rodzaju (tzn. odrzucamy hipotezę prawdziwą, o której w gruncie rzeczy nie wiemy że jest prawdziwa), ale w tym ostatnim przypadku częstość popełnienia takiego błędu jest tylko 1 na 100 przypadków stosowania tego testu istotności.

Test dla wartości średniej populacji

Model I

Populacja generalna ma rozkład normalny N(m, σ) przy czym odchylenie standardowe σ jest znane. Sprawdzamy na podstawie wyników próby losowej n-elementowej hipotezę H₀ : m=m₀

(gdzie m₀ jest konkretną wartością hipotetyczną średniej) wobec hipotezy alternatywnej H₁ : m≠m₀

Na podstawie wyników próby oblicza się wartość statystyki x, tj. średniej z próby, a następnie wartość zmiennej normalnej standaryzowanej U według wzoru

x - m₀

u = σ * pierwiastek z n

Z tablicy rozkładu normalnego N(0,1) wyznacza się taką wartość krytyczną u_α by dla założonego z góry prawdopodobieństwa α (poziomu istotności) zachodziła równość

P{| U | ≥ u_α } = α

Zbiór wartości U określony nierównością | U | ≥ u_α jest obszarem krytycznym tego testu, tzn. gdy z próby otrzymamy taką wartość u, że | u | ≥ u_α to hipotezę H₀ odrzucamy. Gdy zaś | U | < u_α to nie ma wtedy podstaw do odrzucenia hipotezy H₀

Powyższy wzór jest dla testu z dwustronnym obszarem krytycznym, tj. stosowany dla hipotezy alternatywnej w postaci m ≠ m₀

Test z lewostronnym obszarem krytycznym

H₁: m < m₀

wtedy nierówność ma postać U ≤ u_α Wtedy wartość u_α wyznaczamy tak by zachodziła równość

P{ U ≤ u_α} = α

Test z prawostronnym obszarem krytycznym

H₁: m > m₀

U ≥ u_α bo P{U ≥ u_α } = α

Model II.

Populacja generalna ma rozkład normalny N(m, σ) przy czym odchylenie standardowe σ jest nieznane. W oparciu o n elementową próbę losową weryfikuje się hipotezę

H₀ : m = m₀

H₁ : m ≠ m₀

Test istotność jest następujący

Z wyników próby oblicza się wartość średnią X oraz estymator odchylenia standardowego s lub sd (nieobciążone) a następnie wartość statystyki t według wzoru

x - m₀ x - m₀

t = -------------- √ n -1 = -------------- * √n

s sd

Statystyka ma przy założęniu prawdziwości H₀ rozkład Studenta o n-1 stopniach swobody. Z tablicy tego rozkładu dla ustalonego poziomu istotności α i dla n-1 stopni swobody odczytuje się taką wartość t_α że P{ |t| ≥ t_α }= α

Nierówność |t| ≥ t_α określa dwustronny obszar krytyczny

Hipotezę odrzuca się gdy zajdzie nierówność |t| ≥ t_α

W przypadku obszarów lewostronnych lub prawostronnych nierówności przyjmują postać jak w modelu I czyli dla m<m₀ t ≤ t_α a dla m > m₀ t ≥ t_α

Model III

Populacja generalna ma rozkład N(m, σ) lub dowolny inny o wartości średniej m i skończonej wariancji σ² choć nieznanej. Na podstawie wyników dużej próby (n≥30) weryfikuje się hipotezy jak wyżej

Test istotności przyjmuje postać jak w modelu I (czyli ze zmienną U) lecz w miejsce wartości σ przyjmuje się wyznaczoną wartość s z dużej próby

Przykład 1

Pewien automat w fabryce czekolady wytwarza tabliczki czekolady o nominalnej wadze 250 g. Wiadomo, że rozkład wagi produkowanych tabliczek jest normalny N(m, 5). Kontrola techniczna w pewnym dniu pobrała próba 16 tabliczek czekolady i otrzymała z nich średnią wagę 244 g. Czy można twierdzić, że automat rozregulował się i produkuje tabliczki czekolady o mniejszej niż przewiduje norma wadze? Na poziomie istotności α=0,05 zweryfikować odpowiednią hipotezę statystyczną.

Hipoteza ma postać

H₀: m = 250 g

H₁: m < 250 g

Znane jest odchylenie standardowe σ z populacji więc stosujemy model I z lewostronnym obszarem krytycznym

Z tablicy rozkładu normalnego N(0, 1) odczytujemy dla P{ U ≤ u_α }=0,05 wartość u_α = -1,64

Z próby wyznaczamy wartość

244 - 250

u = ----------------- * √16 = - 24 /5 = -4, 8

5

Ponieważ wartość ta znalazła się w obszarze krytycznym

u = -4,8 < - 1,64 = u_α

więc hipotezę H₀ należy odrzucić na korzyść alternatywnej.

Oznacza to, że z prawdopodobieństwem błedu mniejszym niż 0,05 możemy twierdzić, że średnia waga produkowanych obecnie tabliczek czekolady jest za niska (mówi się istotnie niższa) w stosunku do wagi nominalnej i automat należy uregulować.

Przykład 2

W szpitalu wylosowano niezależnie spośród pacjentów leczonych na pewną chorobę próbę 26 chorych i otrzymano dla nich średnią ciśnienia tętniczego krwi x=135 oraz odchylenie standardowe s=45. Należy na poziomie istotności α=0,05 zweryfikować hipotezę, że pacjenci ci pochodzą z populacji o średnim ciśnieniu tętniczym 120.

Odchylenie standardowe populacji (generalnej) nie jest znane, a próba jest mała.

Jest to więc model II z dwustronnym obszarem krtycznym.

Z tablicy rozkładu t-Studenta należy odczytać taką wartość t_α że dla α=0,05 i dla n-1=25 stopni swobody P{ | t_α | ≥ t} = 0,05

wartością tą jest t=2,06

Należy obliczyć wartość t

t=((x-m0)/s) * √n-1 = (135-120)/45 * 5 =15/9=1,67

|t|=1,67 < 2,06=t_α

Oznacza to, że nie znaleźliśmy się w obszarze krytycznym, zatem nie ma podstaw do odrzucenia hipotezy H₀ . Róznica uzyskana z próby nie jest w stosunku do hipotetycznej wartości statystycznie istotna, tzn. da się usprawiedliwić przypadkiem

Z1

Miesięczne dodatkowe dochody studentów w zbadanej grupie 120 osób były następujące

dochody l. studentów

150-250 7

250-350 10

350-450 21

450-550 30

550-650 19

650-750 15

750-850 10

850-950 6

950-1050 2

Na poziomie istotnośc α=0,10 zweryfikować hipotezę, że średni dochód studentów tej uczelni wynosi 500 zł.

Z2

Na podstawie danych liczbowych sprawdzić na poziomie istotności α=0,05 że średni czas snu pacjentów wynosi 7 godzin

Z3

Wylosowano 10 gospodarstw rolnych i otrzymano wielkości uzyskanych plonów. Zweryfikować hipotezę (α=0,1) że średni plon w tej wsi wynosi 18q/ha

Test dla dwóch średnich

Typowymi zastosowaniami tego testu jest porównanie metody nowej ze stary, populacji zdrowych z populacją chorych itd.

W zależności od ilości posiadanych informacji wyróżniamy trzy modele. W każdym z nich weryfikować można hipotezę H₀ : m₁ = m₂ czyli m₁ - m₂ =0 gdzie m₁ i m₂ to wartości średnie pierwszej i drugiej populacji generalnej..

Model I

Badamy 2 populacje generalne o rozkładzie normalnym N(m₁ , σ₁ ) i N(m₂ , σ₂ ). Odchylenia standardowe σ1 i σ2 tych populacji są znane. W oparciu o wyniki dwu niezależnych prób, odpowiednio o liczebnościach n₁ i n₂, należy sprawdzić hipotezę H₀: m₁=m₂, wobec hipotezy alternatywnej H₁: m₁≠ m₂.

Z wyników prób losowych obliczamy wartości średnie x₁ i x₂ a następnie wartość statystyki U wg wzoru

x₁ - x₂

u = -------------------------------

√( σ₁² / n₁ + σ₂² / n₂ )

Statystyka przy założeniu prawdziwości hipotezy H₀ ma rozkład N(0,1).

Z tablicy rozkładu normalnego N(0,1) należy dla przyjętego poziomu istotności α wyznaczyć taką wartość krytyczną u_α by spełniona była równość

P{ |U| ≥ u_α }=α

Nierówność określa dwustronny obszar krytyczny, czyli gdy przy porównywaniu wartości u wyznaczonej z wzoru z wartością u_α odczytaną z tablicy zajdzie nierówność |u|≥u_α to sprawdzaną hipotezę H₀ odrzucamy na korzyść jej alternatywy H₁ .

Dla hipotezy alternatywnej H₁: m₁ < m₂ stosujemy test z lewostronnym obszarem krytycznym U ≤ u_α

Dla hipotezy H₁: m₁ > m₂ stosujemy test z prawostronnym obszarem krytycznym U ≥ u_α . Wartość krytyczną u_α odczytujemy tak by zachodziła P{U≥u_α }=α

Model II

Badamy 2 populacje generalne o rozkładzie normalnym przy czym odchylenia standardowe σ tych populacji są nieznane ale jednakowe, tzn. zachodzi σ₁=σ₂ Na podstawie wyników dwu małych prób o liczebnościach n₁ i n₂ wylosowanych niezależnie weryfikujemy hipotezy jak w modelu I

Z wyników obu tych prób obliczamy wartości średnie x oraz wariancje s² a następnie wartość statystyki t z wzoru

x₁ - x₂

t =----------------------------------------------------------------------

√ ((( n₁*s₁² +n₂*s₂² ) / (n₁ + n₂ -2) ) * (1/n₁ + 1/n₂) )

Statystyka ta ma przy założeniu prawdziwości hipotezy H₀ rozkład t Studenta o n₁+n₂-2 stopniach swobody. Z tablicy rozkładu t-Studenta należy odcczytać dla α i n1+n2-2 stopni swobody taką wartość krytyczną t_α by spełniona była równość

P{|t|≥t_α }=α

gdy nierówność |t|≥t_α jest spełniona to hipotezę H₀ odrzucamy.

Czasem zdarza się, że wyniki obu prób możemy traktować jako wyniki pomiarów na tym samym elemencie populacji. Jest tak wtedy, gdy stanowią one pary uporządkowanych sobie liczb. Typową sytuacją jest tu model: wynik x_i przed jakąś operacją i wynik y_i po niej dla tego samego i.

Wtedy należy analizować wyniki obu prób jako wyniki jednej próby biorąc różnice y_i - x_i, a zamiast testu zamieszczonego w modelu II użyć testu dla średniej różnicy

z_i

t = ----- √ (n-1)

s_z

gdzie z_i = y_i - x_i a n jest liczbą par. Weryfikujemy hipotezę H₀: Z=0 gdzie Z oznacza średnią w populacji

Model III

Badamy 2 populacje generalne mające rozkłady normalne lub inne, byle o skończonych wariancja σ₂ , które nie są znane. Na podstawie wyników dwóch dużych prób n > 30 weryfikujemy hipotezę

Test istotności dla sprawdzanej hipotezy H0 budujemy analogicznie jak w modelu I, z tą różnicą, że przy obliczeniach wartości u zamiast nieznanych wariancji σ₂ przyjmujemy wartości s² uzyskane z dużych prób.

x₁ - x₂

u = -------------------------------

√( s₁² / n₁ + s₂² / n₂ )

Przykład I

Pragniemy stwierdzić, czy słuszne jest mniemanie, że zatrudnione na tych samych stanowiskach kobiety otrzymują przeciętnie niższą płacę niż mężczyźni. Z populacji kobiet zatrudnionych na określonych stanowiskach wylosowano w tym celu niezależnie próbę n₁ =100 kobiet i otrzymano z niej średnią płacę x₁ = 2180 zł oraz wariancję płac s₁² =6400. Z populacji mężczyzn zatrudnionych w tym przemyśle na tych samych stanowiskach wylosowano niezależnie n₂=80 mężczyzn i otrzymano średnią płacę x₂ = 2280 zł oraz wariancję s₂² = 10000. Na poziomie istotności α=0,01 należy sprawdzić hipotezę, że średnie płac kobiet są niższe.

Z treści wynika, że nie znamy wariancji, ale mamy duże próby. Mamy więc do czynienia z modelem III.

Hipotezę badawczą o niższych przeciętnie zarobkach kobiet zamieniamy na hipotezę statystyczną, że średnie zarobki kobiet m₁ oraz mężczyzn m₂ są takie same i zależy nam oczywiście na odrzuceniu tej ostatniej hipotezy statystycznej. Formalnie rzecz biorąc, stawiamy hipotezę

H₀: m₁=m₂ wobec hipotezy alternatywnej H₁: m₁ < m₂

Obliczamy wartość u

2180-2280 -100

u = -------------------- = ----------------- = -7,27

√ ( 6400/100 + 10000/80) √ 189

Z tablicy rozkładu N(0,1) należy odczytać w taki sposób krytyczną wartość u_α by P{U≤u_α }=0,01

Jest to wartość u_α = -2,33

U=-7,27 < - 2,33 = u_α

znaleźliśmy się w obszarze krytycznym, zatem hipotezę H₀ o równości średnich odrzucamy na korzyść alternatywy H₁

Otrzymany wynik oznacza, że rzeczywiście w tym przemyśle kobiety zarabiają przeciętnie mniej niż mężczyźni zatrudnieni na tych samych stanowiskach. Często mówi się że (dla α=0,001) otrzymana różnica średnich (100 zł) jest statystycznie bardzo istotna.

Przykład II

Wysunięto hipotezę, że czas potrzebny na obróbkę metalowego detalu można zmniejszyć przez zastosowanie innego niż dotychczas typu obrabiarki. Zmierzono czasy wykonywania detalu dla obrabiarki nowej II następujące wyniki w min: 15,12,10,18,14,15,13

a dla obrabiarki I starej : 17,11,22,18,19,13,14,16

Zweryfikować hipotezę na poziomie α=0,05

Ze względu na małe próby stosujemy model II

n₁=8 n₂=7

Stawiamy hipotezę H₀: m₁=m₂ wobec H1: m₁ > m₂ gdzie m₁ oznacza średni czas toczenia przy użyciu obrabiarki starej, a m₂ - nowej.

Dla α=0,05 oraz dla n₁+n₂-2=13 stopni swobody mamy t_α =1,771

zauważamy, że n₁s₁² = suma (x_i1 - xsr₁)²

wystarczy zatem obliczyć średnie x oraz sumy kwadratów odchyleń od nich

x1=16 min x2=14 min n1s1² =88, m2s2² =39

16-14 2

t = ------------------------------------------------ = ----------------------=1,23

√ ( (88+39)/(8+7-2) * (1/8 + 1/7) √ (2,62)

t=1,23 < 1,771=t_α czyli nie znaleźliśmy się w obszarze krytycznym t≥t_α. Nie ma więc podstaw do odrzucenia hipotezy H₀ I oznacza to, że różnica średnich czasów toczenia obu metodami nie jest statystycznie istotna i da się usprawiedliwić przypadkiem. Nie została zatem udowodniona przewaga nowej obrabiarki.

Z1

Pojemność życiowa płuc studentów uprawiających czynnie sport ma odchylenie standardowe 440 cm3,natomiast studentów nie uprawiających 620 cm3. Wylosowano próbę z sportowców n=20 x=4080 cm3, a dla nie uprawiających sportu n=15 x=3610. Przyjmując α=0,05 sprawdzić hipotezę, że uprawianie przez studentów sportu zwiększa pojemność życiową ich płuc

Z2

W grupie pacjentów leczonych na nadciśnienie podawano lek. Otrzymano pomiary. Zweryfikować hipotezę, że lek powoduje spadek ciśnienie u pacjentów.

Test dla wskaźnika struktury (procentu)

W badaniu statystycznym prowadzonym ze względu na cechę niemierzalną (jakościową) zachodzi czasem konieczność sprawdzenia hipotezy o wartości wskaźnika struktury populacji tj. frakcji elementów wyróżnionych w populacji (lub po przemnożeniu przez 100 - procentu)

Model.

Populacja generalna ma rozkład dwupunktowy z parametrem p, tzn. frakcja elementów wyróżnionych w populacji jest p. Z populacji tej wylosowano niezależnie do próby dużą liczbę n elementów populacji n>100 W oparciu o wyniki tej próby należy zweryfikować hipotezę H₀: p=p₀ wobec hipotezy alternatywnej H₁: p≠p₀ gdzie p₀ jest hipotetyczną wartością parametru p.

Test istotności dla tej hipotezy jest następujący

Obliczamy wskaźnik struktury z próby m/n gdzie m jest liczbą elementów wyróznionych znalezioną w próbie. Następnie obliczamy wartość statystyki

m/n - p₀

u=---------------------------

√( (p₀*q₀)/n)

gdzie q₀=1-p₀

Statystyka ta ma przy założeniu prawdziwości hipotezy H0 rozkład asymptotycznie normalny N(0, 1). Z tablicy rozkładu normalnego znajdujemy taką krytyczną wartość u_α by spełniona była równość

P{|U|≥u_α }=α

Zbiór określony nierównością jest dwustronnym obszarem krytycznym.

gdy z porównania wartości u z wartością krytyczną u_α wyniknie, że |u|≥u_α wówczas hipotezę H₀ odrzucamy na korzyść alternatywy H₁

dla hipotezy alternatywnej w postaci H₁:p<p₀ obszar krytyczny U≤u_α

dla H1:p>p₀ obszar krytyczny U>p₀

P1

Wysunięto hipotezę, że wadliwość produkcji pewnego zespołu w aparatach radiowych wynosi 10%. W celu sprawdzenia tej hipotezy wylosowano niezależnie próbę 100 podzespołów i otrzymano w niej 15 podzespołów wadliwych. Na poziomie istotności α=0,05 zweryfikować hipotezę.

m/n = 15/100 = 0,15=15% wadliwych podzespołów

Obszar krytyczny testu można zbudować dwustronnie.

Stawiamy hipotezę H₀ : p=0,1 wobec H₁: p≠0,1

Z tablicy rozkładu normalnego N(0,1) odczytujemy taką wartość u_α by P(|U|≥u_α}=0,05 jest towartość u_α=1,96

Na podstawie wzoru obliczamy u

0,15-0,10 0,05

u = -----------------------------------= ------------ =1,67

√(0,1*0,9/100) 0,03

|u|=1,67 < 1,96=u_α

Nie ma podstaw do odrzucenia hipotezy H₀, że wadliwość wynosi 10%. Różnica 5% otrzymana w próbie okazała się nieistotna.

Z1

W magazynie wylosowano 120 składowanych skrzynek z cytrusami, po zbadaniu okazało się że w 16 skrzyniach znaleziono zepsute owoce. Na poziomie α=0,05 zweryfikować tezę, że przechowywana partia zawiera więcej niż 5% skrzynek z zepsutymi cytrynami.

Z2

Na podstawie 800 zbadanych pacjentów 320 miało grupę krwi zero. Na poziomie istotności α=0,05 zweryfikować hipotezę, że procent pacjentó z tą grupą wynosi 35%.

Z3

W badaniach ankietowych wylosowano 800 studentów. Na pytanie, czy student po ukończeniu studiów pragnie pracować w swym rodzinnym powiecie, odpowiedziało tak 120. czy na poziomie istotności α=0,01 można odrzucić hipotezę, że procent tych studentów w populacji wynosi 20%?

Test dla dwóch wskaźników struktury (procentów)

Badając dwie populacje ze względu na cechę niemierzalną często musimy sprawdzić, czy frakcje elementów wyróżnionych w obu populacjach są takie same.

Test opisany poniżej może być zastąpiony testem niezależności χ² dla czteropolowej tabicy niezależności.

Model

dane są dwie populacje generalne o rozkładach dwupunktowych z parametrami odpowiednio p₁ i p₂ Na podstawie dwu dużych prób n>100 o liczebnościach n₁ i n₂ należy sprawdzić hipotezę H₀:p₁=p₂ wobec H1:p₁≠p₂

Test istotności dla tej hipotezy jest następujący. Z obu prób wyznaczamy parametry m₁ i m₂ elementów wyróżnionych w próbach.

następnie obliczamy wartość średniego wskaźnika struktury z obu prób p(śr.)

m₁+m₂

p=--------------

n₁+n₂

oraz

n₁*n₂

n=---------------

n₁+n₂

wartość pseudoliczebności z próby n.

Następnie obliczamy wartość statystyki u

m₁/n₁ - n₂/n₂

u= ------------------------------ gdzie q=1-p(śr)

√ ((p * q )/n)

obszar krytyczny jest określony nierównością |u|≥u_α

P1

W celu sprawdzenia, czy zachorowalność na gruźlicę jest w pewnym województwie taka sama w mieście jak i na wsi, pobrano z ludności wiejskiej i miejskiej dwie losowe próby, mianowicie z ludności miejskiej wylosowano n₁=1200 osób i otrzymano m₁=40 chorych

a z ludności wiejskiej wylosowano n₂=1500 osób i otrzymano m₂=100 chorych

Przyjmując poziom istotności α=0,05 należy zweryfikować hipotezę o jednakowym procencie chorych na gruźlicę w mieści i na wsi w tym województwie.

Hipoteza jak w modelu z dwustronnym obszarem krytycznym

m₁/n₁ = 40/1200 = 0,033 = 3,3%

m₂/n₂=100/1500=0,067=6,7%

_ _

p = (m1+m2)/(n1+n2)=140/2700=0,052 q=0,948

n=n1*n2/(n1+n2)=1200*1500/(1200+1500)=18000/27=667

u=(0,033-0,067)/(pierw(0,052*0,948/667))=-0,034/pierw(0,0000739)≈-3,9

|u|=3,9>1,96=u_α

Hipotezę odrzucamy. Nie można twierdzić, że w tym województwie jednakowa jest zachorowalność na gruźlicę na wsi i w mieście.

Z1

Wysunięto przypuszczenie, że jakość produkcji pewnego wyrobu po wprowadzeniu nowej, tańszej technologii, nie uległa zmianie. Sprawdzić hipotezę o jednakowym odsetku braków przy produkcji obu metodami

Z2

W pewnym doświadczeniu farmakoloigcznym otrzymano na 120 badanych szczurów, którym podano preparat, 57 takich, które doszły do pokarmu w labiryncie w czasie 1 minuty. Natomiast na 100 szczurów, którym nie podano preparatu, 71 wkonało to zadanie w tym samym czasie. Zweryfikować hipotezę o otępiającym działaniu badanego preparatu na szczury.

Z3

Badając wpływ nowego leku na poprawę stanu zdrowia chorych na cukrzycę podano n1 chorym nowy lek i u m1 z nich stwierdzono powrót poziomu cukru do normy. Natomiast w drugiej grupie n2 badanej chorych leczonych metodami tradycyjnymi u m2 stwierdzono poprawę. Zweryfikować hipotezę o większym procencie wyzdrowień w grupie pacjentó leczonych nowym lekiem.

Test dla wariancji populacji generalnej

Wariancja jako miara rozproszenia (rozrzutu) wartości badanej cechy bywa szczególnie często w różnych badaniach naukowych wykorzystywana do oceny stopnia jednorodności czy też powtarzalności wyników liczbowych uzyskiwanych w eksperymentach. W szczególności ocena dokładności przyrządu pomiarowego, za pomocą którego mierzy się wyniki eksperymentu, wymaga często sprawdzenia hipotez o wariancji σ² populacji. W odróżnieniu od odchylenia standardowego rozkład estymatora s² jest znany i stablicowany - χ² Wygodnie więc jest sprawdzić hipotezy nie o wartości odchylenia standardowego lecz o wariancji.

Rozkład χ² został powszechnie stablicowany do 30 stopni swobody. Ze względu na szybką zbieżność tego rozkładu do rozkładu normalnego, gdy liczba stopni swobody rośnie nieograniczenie, w praktycznych przypadkach w rozkładzie χ² dla liczby stopni swobody większej niż 30 można już korzystać z rozkładu normalnego..

Mianowicie, gdy liczba stopni swobody k w rozkładzie χ² dąży do nieskończoności, dystrybuanta zmiennej losowej √ (2χ² ) dąży do dystrybuanty rozkładu normalnego N(√ 2k-1, 1)

Dla liczby stopni swobody k > 30 zamiast tablicy rozkładu χ² korzystamy z tablicy rozkładu N(0,1) dla zmiennej √ (2χ² ) - √ (2k-1)

Ze względu na to, że zwykle w praktyce jedynie większa wariancja od pewnej ustalonej jest niekorzystna, w poniższym teście istotności dla wariancji przyjmuje się zwykle obszar krytyczny prawostronny.

Model

Populacja generalna ma rozkład normalny N(m,σ) o nieznanych parametrach m i σ. Z populacji tej wylosowano niezależnie n elementów do próby, na podstawie której należy sprawdzić hipotezę

H₀:σ² =σ₀² wobec hipotezy alternatywnej H₁:σ² > σ₀²

gdzie σ₀² jest hipotetyczną wartością wariancji σ²

Test istotności dla tej hipotezy jest następujący

Z wyników n elementowej próby losowej obliczamy wartość s² , następnie statystyki

ns² (n-1)s_n²

χ² = ----------- = ------------------------- = 1/σ₀² * ∑ (dla i=1 do n) (x_i-xśr)²

σ₀² σ₀²

gdzie s_n to odchylenie standardowe nieobciążone (to z daszkiem)

xśr to średnia arytmetyczna

Statystyka ta ma przy założeniu prawdziwości hipotezy H₀ rozkład χ² z n-1 stopniami swobody.

Dla ustalonego z góry poziomu istotności α i dla n-1 stopni swobody odczytujemy z tablicy rozkładu χ² taką wartość krytyczną χ_α² aby spełniona była równość

P{χ² ≥ χ₀² }=α

Nierówność χ² ≥ χ_α² określa prawostronny obszar krytyczny (a więc obszar dla odrzucenia hipotezy H₀). Jeśli nierówność jest prawdziwa to hipotezę H₀ odrzucamy. Jeśli zaś χ² <χ_α² to nie ma podstaw do odrzucenia hipotezy że wartość wariancji σ² populacji generalnej jest σ₀²

Krzywa rozkładu χ² nie jest symetryczna. Lewy obszar jest wyższy niż obszar prawy, który jest spłaszczony, rozciągnięty.

P1

Dokonano 12 pomiarów woltomierzem pewnego napięci prądu i otrzymano z tej próby sd² (s² nieobciążone) 0,9V² . Należy na poziomie istotności α=0,05 sprawdzić hipotezę, że wariancja pomiarów napięcia tym woltomierzem wynosi 0,6V²

W celu stwierdzenia, czy wariancja pomiarów nie jest większa od wariancji hipotetycznej, stawiamy hipotezę H₀:σ² =0,6, wobec hipotezy alternatywnej H₁:σ² >0,6

Na podstawie wzoru wyznaczamy wartość statystyki

χ² = (11*0,9)/0,6 = 16,5

Dla przyjętego poziomu istotności α=0,05 i dla n-1=11 stopni swobody odczytujemy χ_α²

Tablice podają prawdopodobieństwo zdarzenia określone nierównością z modelu, a więc

P(χ² ≥ χ_α² )=α

χ_α² =19,675

χ² =16,5 < 19,675=χ_α²

Nie znaleźliśmy się w obszarze krytycznym, nie ma więc podstaw do odrzucenia hipotezy H₀. Oznacza to, że w próbie przypadkowo otrzymano wariancję większą niż hipotetyczna.

Nie można powiedzieć, że rozproszenie wyników pomiarów napięcia tym woltomierzem jest większe niż założone.

Gdyby w powyższym przykładzie tę samą wariancję sd² =0,9 uzyskano z próby 61 pomiarów (próba duża), wówczas otrzymalibyśmy wartość statystki χ² =90

Ponieważ liczba stopni swobody w tablicach wynosi co najwyżej 30, więc w tym przypadku należałoby skorzystać z granicznego rozkładu normalnego, do którego dąży rozkład χ²

Otrzymaną wartość χ² przekształcamy na u=√ (2χ² ) - √ (2k-1) i porównujemy z wartością u_α zmiennej normalnej N(0,1) odczytaną tak by

P(U≥ u_α}=0,05

Otrzymalibyśmy wtedy

u=√ (2*90)-√ (2*60-1)=√ 180 - √ 119 = 13,4-10,9 ≈ 2,5

u_α=1,64

zatem u=2,5 > 1,64=u_α

zatem hipotezę H₀ należałoby odrzucić.

Z1

Dokonano 11 pomiarów średnicy odlewanych rur. Na poziomie istotności α zweryfikować hipotezę, że wariancja uzyskiwanych średnic rur jest 0,04

Z2

na podstawie danych liczbowych zweryfikować hipotezę, że wariancja plonów owsa w indywidualnych gospodarstwach rolnych wynosi 0,25 (q/ha)²

Test dla dwóch wariancji

Najczęściej podany tu test służy jako sprawdzenie założenia wymaganego przy teście t-Studenta dla dwu średnich. Założenie występujące tam dotyczy właśnie równości wariancji w obu populacjach, których średnie chcemy porównać.

Rozkładem, który posługujemy się w tym teście jest rozkład F Snedecora. Ze względu na to, że dostępne tablice tego rozkładu zostały sporządzone tak, iż podają taką wartość F_α , dla której zachodzi równość P{F≥ F_α}=α, w omawianym teście obszar krytyczny jest prawostronny. Dlatego oznaczenia populacji numerami 1 i 2 należy tak przyjąć, aby w ilorazie dwu wariancji z prób licznik był zawsze większy od mianownika. Przy odczytywaniu z rozkładu F Snedecora wartości krytycznej F_α dla tego testu należy pamiętać, że występują w nim dwa rodzaje stopni swobody - licznika i mianownika, przy czym w tabelach tego rozkładu w główce umieszczone są stopnie swobody licznika, a w boczku stopnie swobody mianownika.

W omawianym teście wygodniej jest używać statystyki s² nieobciążone

^s² =1/(n-1) ∑ (x_i - xśr)² dla i=1 do n

jeśli więc obliczono tylko s² można przekształcić ją na wartość ^s² wg wzoru

^s² = (n/(n-1)) * s²

Model

Dane są dwie populacje generalne mające odpowiednio rozkłady normalne N(m₁, σ₁) i N(m₂, σ₂) gdzie parametry tych rozkładów są nieznane. Z populacji tych wylosowano niezależnie dwie próby o liczebności n₁ i n₂ elementów. Na podstawie wyników tych prób należy sprawdzić hipotezę H₀:σ₁² =σ₂² wobec hipotezy alternatywnej H₁: σ₁² > σ₂²

Test istotności dla tej hipotezy jest następujący.

Z obu prób wyznaczamy wartości ^s₁² i ^s₂² przy czym ^s₁² >s₂² . Z kolei wyznaczamy według wzoru

F= ^s₁² / ^s₂²

wartość statystyki F, która przy założeniu prawdziwości hipotezy H₀ ma rozkład F Snedecora z n₁-1 i n₂-1 stopniami swobody.

Dla ustalonego z góry poziomu istotności α odczytujemy z tablicy rozkładu F Snedecora wartość krytyczną F_α tak by spełniona była równość P(F≥ F_α) = α.

Nierówność F≥ F_α określa prawostronny obszar krytyczny, więc gdy zajdzie nierówność hipotezę H₀ odrzucamy, gdy zaś F<F_α nie ma podstaw do odrzucenia hipotezy o równości wariancji.

Rozkład F Snedecora ma kształt podobny do rozkładu χ²

P1

Przed zastosowaniem testu t-Studenta dla hipotezy, że średnie zarobki pracowników zatrudnionych na tych samych stanowiskach roboczych w dwu różnych fabrykach są jednakowe, należy sprawdzić założenie tego testu, że wariancje zarobków w obu fabrykach są identyczne.

Z jednej fabryki wylosowano w tym celu niezależnie 16 pracowników i otrzymano z tej próby wariancję ^s² =22500 (zł)² . Natomiast z drugiej fabryki wylosowano 21 pracowników do próby i otrzymano z niej ^s² =40000 (zł)² . Można przyjąć, że rozkłady zarobków w obu fabrykach są normalne. Na poziomie istotności α=0,05 sprawdzić hipotezę, że wariancje zarobków badanych pracowników są takie same w obu fabrykach.

Aby otrzymać w tym teście większą wartość należy oznaczyć

n₁=21 i ^s₁² =40000 oraz n₂=16 i ^s₂² =22500

F=40000/22500 = 1,78

F_α=2,33

F=1,78 < 2,33=F_α

zatem nie ma podstaw do odrzucenia hipotezy H₀, że wariancje zarobków w obu populacjach pracowników są jednakowe. W następstwie otrzymanego wyniku możliwe jest zastosowanie testu t-Studenta dla średnich zarobków w obu fabrykach.

Z1

W celu sprawdzenia dokładności pomiarów natężenia prądu dwoma różnymi amperomierzami, wykonano 7 pomiarów natężenia prądu 7A jednym ampteromierzem oraz 6 pomiarów natężenia prądu 4A drugim amperomierzem. Na poziomie istotności α sprawdzić hipotezę o jednakowej wariancji pomiarów natężenia prądu obu amperomierzy.

Test jednorodności wielu wariancji Bartletta

Test dotyczy przypadku populacji normalnych, dla których chcemy sprawdzić hipotezę o równości wariancji we wszystkich populacjach.

Aby uniknąć kłopotów z logarytmami naturalnymi, poniżej będzie podana postać wzoru z wykorzystaniem jedynie logarytmów dziesiętnych - stąd stała 2,303 występująca we wzorze.

Model

Danych jest k populacji normalnych N(m_i, σ_i) (i=1,,,j}. Z każdej tych populacji wylosowano niezależnie do próby n_i elementów. Mamy więc k losowych prób o liczebnościach n_i. Wyniki każdej próby oznaczamy symbolem x_ij (i=1...k, j=1..n_i}, a ich srednie symbolem _x_i. Na podstawie wyników tych prób chcemy sprawdzić hipotezę o jednakowych wariancjach we wszystkich populacjach, tj. hipotezę H₀: σ₁² =σ₂² =...σ_k² wobec hipotezy alternatywnej H₁: nie wszystkie te wariancje są równe.

Z wyników prób o liczebnościach n_i obliczamy według wzorów kolejno

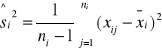
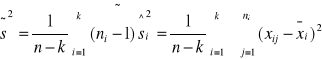
gdzie n=∑n_i dla i=1 do k

Następnie obliczamy wartość statystyki χ² wg wzoru

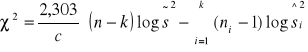
Statystyka ta ma przy założeniu prawdziwości hiptezy H₀ rozkład asymptotyczny χ² z k-1 stopniami swobody. Z tablicy rozkładu χ² dla ustalonego poziomu istotności α i dla k-1 stopni swobody odczytujemy wartość krytyczną χ_α² w taki sposób, by zachodził P{χ² ≥ χ_α² }=α. Nierównośc χ² ≥ χ_α² określa prawostronny obszar krytyczny dla tego testu. Jeśli więc spełniona jest powyższa nierówność to hipotezę H₀ odrzucamy.

P

Należy sprawdzić, czy trzy rózne metody produkcji pewnego wyrobu charakteryzują się taką samą wariancją wydajności pracy robotników stosujących je. Losowo zmierzone wydajności pracy przy produkcji tego wyrobu w liczbach sztuk na godzinę są następujące:

metoda I	2	5	3	6	4	n1=5
metoda II	10	12	12	14		n2=4
metoda III	20	23	26	24	22	n3=5

Na poziomie istotności α=0,05 należy zweryfikować hipotezę o jednorodności wariancji wydajności pracy robotników pracujących tymi trzema metodami.

Zakładając zbliżony do normalnego rozkład wydajności pracy dla tych metod, stawiamy formalnie rzecz biorąc hipotezę H₀:σ₁² =σ₂² =σ₃² , wobec hipotezy alternatywnej H₁: nie wszystkie wariancje są sobie równe.

x1j	x2j	x3j	(x1j-_x1)^2	(x2j-_x2)^2	(x3j-_x3)^2
2	10	20	4	4	9
5	12	23	1	0	0
3	12	26	1	0	9
6	14	24	4	4	1
4	-	22	0	-	1
20	48	115	10	8	20

_x₁=4

_x₂=12

_x₃=23

^s₁² =2,50

^s₂² =2,67

^s₃² =5,00

~s² =(1/(14-3))*38 = 3,45

^si^2	log^si^2	ni-1	(ni-1)log^si^2
2,50	0,398	4	1,592
2,67	0,426	3	1,278
5,00	0,699	4	2,796
			5,666

Stąd

log ~s² =log3,45=0,538

(n-k)log~s² =(14-3)*0,538=5,918

c=1+(1/(3*2))*[(1/4 + 1/3 + ¼)-1/11]=1,124

Obliczamy

χ² =2,303/1,124 * (5,918-5,666)=0,516

Dla α=0,05 i k-1=2 stopni swobody wartość χ_α² =5,99. Ponieważ otrzymaliśmy χ² =0,516<5,99=χ_α² przeto nie ma podstaw do odrzucenia hipotezy H₀. Oznacza to, że nie udowodniono róznego stopnia rozproszenia wydajności pracy przy badanych trzech róznych sposobach produkcji danego wyrobu

Test analizy wariancji (klasyfikacja pojedyncza) dla wielu średnich

Testy analizy wariancji są podstawowym narzędziem statystyki eksperymentalnej, tj. szeroko rozbudowanej dla potrzeb doświadczalnictwa rolnego, medycznego, statystycznej metody planowania i oceny wyników eksperymentów naukowych. Testy te pozwalają na sprawdzenie, czy pewne czynniki, które można dowolnie regulować w toku eksperymentu, wywierają wpływ, a jeśli tak, to jak wielki, na kształtowanie się średnich wartości badanych cech mierzalnych. Istotą analizy wariancji jest rozbicie na addytywne składniki (których liczba wynika z potrzeb eksperymentu) sumy kwadratów wariancji całego zbioru wyników. Prównanie poszczególnej wariancji wynikającej z działania danego czynnika oraz tzw. wariancji resztowej, czyli wariancji mierzącej losowy błąd (które to proównanie odbywa się przez zastosowanie testu F Snedecora) daje odpowiedź, czy dany czynnik odgrywa istotną rolę w kształtowaniu się wyników eksperymentu.

W tym miejscu zostanie przedstawiona analiza mająca zastosowanie w ogólnej statystyce, nie tylko doświadczalnej.

Klasyfikacja pojedyńcza

Sumę kwadratów wariancji ogólnej rozbija się tu jedynie na dwa składniki mierzące zmienność między grupami (populacjami) i wewnątrz grup. Porównując testem F wariancję między grupami z wariancją wewnętrzną grup rozstrzygamy, czy średnie grupowe różnią się istotnie od siebie czy nie. Jeżeli podział na grupy np. przebiegał ze względu na różne poziomy badanego czynnika, to można w ten sposób wykryć wpływ poziomu na efekt wartości badanej cechy.

Test analizy wariancji zwykle przeprowadza się według określonego schematu, ujętego w postaci tzw. tablicy analizy wariancji, mającej różną liczbę wierszy w zależności od konkretnego schematu, ale kolumny zawsze następujące.

źródło zmienności	Suma kwadratów	Stopnie swobody	Wariancja	Test F

Do tabelki tej wpisuje się odpowiednie dane liczbowe obliczone z wyników próby. Dzieląc odpowiednią sumę kwadratów przez stopnie swobody otrzymujemy pewne oceny wariancji, które porównujemy testem F z wariancją resztową na przyjętym poziomie istotności. Jeżeli F≥ F_α, to efekt danego czynnika jest istotny.

Testem podanym w tym modelu weryfikuje się hipotezę, że średnie wartości wielu populacji są takie same. Potrzebne w tym teście założenie jednorodności wariancji można sprawdzić testem Bartletta.

Model

Danych jest k populacji o rozkładzie normalnym N(m_i, σ_i) (i=1, 2,..., k) lub o rozkładzie zbliżonym do normalnego. Zakłada się przy tym, że wariancje wszystkich k populacji są równe, tzn. σ₁² =σ₂² =...=σ_k² =σ² (lecz nie muszą być znane). Z każdej z tych populacji wylosowano niezależnie próby o liczebności n_i elementów. Wyniki prób oznaczone są przez x_ij (i=1, 2, ..., k, j=1, 2, ..., n_i) przy czym x_ij=m_i+ε_ij , gdzie ε_ij jest wartością zmiennej losowej nazywanej składnikiem losowym, mającej rozkład N(0,σ). Na podstawie wyników x_ij należy zweryfikować hipotezę H₀: m₁=m₂=...=m_k wobec hipotezy alternatywnej H₁: nie wszystkie średnie badanych populacji są równe.

Test istotności dla tej hipotezy jest następujący

Obliczamy z wyników poszczególnych prób średnie grupowe _x_i i średnią ogólną ⁼x (dwie kreski u góry).

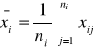
dla i=1, 2, ..., k,

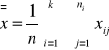
gdzie

Z kolei obliczamy odpowiednie sumy kwadratów i wypełniamy wartościami liczbowymi następującą tablicę analizy wariancji; występująca w niej statystyka F ma przy założeniu prawdziwości hipotezy H₀ rozkład F Snedecora o k-1 i n-k stopniach swobody:

Zródło zmienności	Suma kwadratow	Stopnie swobody	Wariancja	Test F
między populacjami (grupami)		k-1	^s1^2
wewnętrz grup (składnik losowy)		n-k	^s2^2

Obliczoną w tablicy analizy wariancji wartość F porównujemy w końcu z wartością krytyczną F_α odczytaną z tablicy rozkładu F Snedecora dla ustalonego z góry poziomu istotności α i dla odpowiedniej liczby k-1 oraz n-k stopni swobody. Spełniona ma być przy tym równość P(F≥ F_α)=α. Jeżeli spełniona jest nierówność F≥ F_α to hipotezę H₀ należy odrzucić.

Gdy F<1 to bez porównywania z F_α nie ma podstaw do odrzucenia hipotezy H₀. Odrzucenie hipotezy H₀ oznacza udowodnienie istotnego wpływu podziału na te populacji. W przeciwnym wypadku wszystkie grupy (populacje) można uznać za równoważne z punktu widzenia otrzymanych wartości badanej cechy.

P

Koszty materiałowe pewnego wyrobu, który można produkować trzema różnymi metodami, mają rozkład normalny o jednakowej wariancji dla każdej z tych metod. Wylosowane sztuki tego wyrobu dały następujące koszty materiałowe dla poszczególnych metod proukcji (w zł)

Metoda
A	B	C
25	40	5
15	20	15
20	25	20
30	50	20
10	10	40
-	35	10
-	-	30

Na poziomie istotności α=0,05 należy zweryfikować hipotezę, że średnie koszty materiałowe są jednakowe dla wszystkich trzech metod produkcji tego wyrobu.

Stawiamy hipotezę H₀:m₁=m₂=m₃ gdzie m₁, m₂, m₃ oznaczają średnie koszty materiałowe odpowiednie dla każdej z metod produkcji. Hipotezę tę można zweryfikować za pomocą testu analizy wariancji w przypadku pojedynczej klasyfikacji. W celu wypełnienia danymi liczbowymi odpowiedniej dla tego testu tablicy analizy wariancji, przeprowadzamy niezbędne obliczenia średnich i i sum kwadratów

n=n₁+n₂+n₃=5+6+7=18

_x₁=100/5=29

_x₂=180/6=30

_x₃=140/7=20

=x = 420/18=23,3

=250

=1050

=850

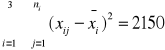
(_x₁ - ⁼x)² *n₁=54,45

(_x₂ - ⁼x)² *n₂ =269,34

(_x₃ - ⁼x)² *n₃ = 76,23

=400,0

Otrzymujemy zatem następującą tablicę analizy wariancji;

Zródło zmienności	Suma kwadratow	Stopnie swobody	Wariancja	Test F
między populacjami (grupami)	400,0	2	200,0	F=200/143,3=1,39
wewnętrz grup (składnik losowy)	2150	15	143,3

Z tablicy rozkładu F Snedecora dla przyjętego poziomu istotności α=0,05 i dla liczby stopni swobody 2 i 15 odczytujemy krytyczną wartość F_α=3,68

Ponieważ nie otrzymaliśmy wartości F z obszaru krytycznego, bo F=1,39 < 3,68=F_α więc nie ma podstaw do odrzucenia hipotezy H₀ o równości średnich kosztów materiałowych przy produkcji tego wyrobu trzeba róznymi metodami. Oznacza to, że nie udowodniliśmy, że metody te dają różne średnie koszty materiałowe tego wyrobu.

Z

Trzech nauczycieli j. polskiego oceniało w skali punktowej wypracowania wylosowanych 4 uczniów pewnej szkoły. Zweryfikować hipotezę, że wszyscy trzej nauczyciele są tak samo surowi (wystawiają średnie oceny takie same)

Z

Na podstawie danych liczbowych zweryfikować hipotezę, że średnie plony pszenicy są takei same przy zastosowaniu trzech róznych kombinajcji nawożenia gleby.

Z

Na podstawie danych liczbowych zweryfikować hipotezę, że średnie wytrzymałości na ściskanie wytworzonych trzech betonów budowlanych są takie same.

Test analizy wariancji (klasyfikacja podwójna)

W zastosowaniach nieraz zachodzi potrzeba klasyfikacji wyników obserwacji według wielu naraz kryteriów. Przy dwóch kryteriach mówimy o tzw. klasyfikacji podwójnej. Z klasyfikacją podwójną mamy do czynienia w takich eksperymentach, w których na realizację badanej zmiennej losowej mogą wpływać dwa niezależne czynniki dające addytywne (sumujące się) efekty.

Podstawą testu analizy wariancji według klasyfikacji podwójnej jest rozbicie sumy kwadratów wariancji wyników próby na trzy składniki odpowiadające zmienności wywoałenj pierwszym czynnikiem, drugim czynnikiem oraz zmienności resztowej.

Klasyfikację n obserwacji zmiennej losowej X na r grup według przyjętego pierwszego kryterium (czynnik A) i na k grup według drugiego kryterium (czynnik B) możemy zapisać jako tablicę.

A/B	1	k
1	x11	x1k
r	x21	xrk

Występujące w tej bablicy liczby x_ij (i=1..r, j=1..k) oznaczają zaobserwowane w doświadczeniu w grupie i (ze względu na czynnik A) oraz w grupie j( ze względu na czynnik B) wartości badanej cechy X.

Należy zwrócić uwagę, że we wnętrzu tablicy wpisuje się nie liczebności, lecz wartości mierzalnej cechy X.

W każdej klasyfikacyjnej podgrupie, tj. w kratce (i,j) występuje tylko jedna obserwacja x_ij (np. ze względu na wysokie koszty eksperymentu),

Model

Danych jest r * k populacji o rozkładzie normalnym N(m_ij, σ), gdzie i=1..r, j=1..k, a σ jest nieznane. Z każdej z tych populacji wylosowano niezależnie do jednej obserwacji x_ij otrzymując r*k obserwacji zestawionych w tablicy o r wierszach i k kolumnach. Na podstawie tych informacji należy zweryfikować hipotezę o ich jednorodności, tj. hipotezę H₀:m₁₁=m₁₂ =...=m_rk że wszystkie wartości średnie m_ij są sobie równe. Hipotezę H₀ na gruncie eksperymentu statystycznego z podwójną klasyfikacją można interpretować jako brak istotnego wpływu klasyfikacyjnych czynników na wartości obserwowanej cechy X

Test istotności dla hipotezy H₀ jest następujący:

Z wyników obserwacji x_ij obliczamy:

średnie arytmetyczne w wierszach

_x_i. = (1/k) ∑ x_ij (dla j=1 do k) i=1..r

średnie arytmetyczne w kolumnach

_x_.j = (1/r) ∑ x_ij (dla i=1.r) j=1..k

średnią arytmetyczną ogólną

_x=(1/rk) * ∑(dla i=1..r) ∑ x_ij (dla j=1 ..k) (suma podwójna)

Z kolei obliczamy sumy kwadratów:

dla zmiennej całkowitej

SK_c=

dla zmienności między wierszami (czynnik A)

SK_A = k * ∑ (_x_i. - _x)² (dla i=1 ..r)

dla zmienności między kolumnami (czynnik B)

SK_B= r * ∑ (_x_.j - _x)² (dla j=1 ..k)

dla zmiennej resztowej

SK_R=
= SK_C - SK_A - SK_B

Dzieląc sumy kwadratów przez odpowiadające im stopnie swobody, otrzymujemy wariancje z próby będące estymatorami wariancji σ² populacji. Wariancje z próby są podstawą obliczenia wartości statystyki F, zgodnie z następującą tablicą analizy wariancji.

Żródło zmienności	Suma kwadratów	Stopnie swobody	Wariancja	Test F
między wierszami (czynnik A)	SKA	r-1	^s1^2	FA=^s1^2 / ^s3^2
między kolumnami (czynnik B)	SKB	k-1	^s2^2	FB=^s2^2 / ^s3^2
resztowa (błąd losowy)	SKR	(r-1)(k-1)	^s3^2

Gdy hipoteza H₀ jest prawdziwa, wtedy statystyka F_A ma rozkład F Snedecora o (r-1) i (k-1) stopniach swobody, natomiast statystyka F_B ma wtedy rozkład F Snedecora o (k-1) i (r-1) stopniach swobody.

Obliczone w tablicy wartości statystyk F_A i F_B porównujemy z odczytanymi z tablicy rozkładu F Snedecora wartościami krytycznymi F_A,α i F_B,α dla przyjętego poziomu istotności α i odpowiednich liczb stopni swobody.

Jeśli zachodzi nierówność F_A ≥ F_A,α to hipotezę H₀ odrzucamy (co oznacza wykazanie istotnego wpływu czynnika A w doświadczeniu). Podobnie jeśli F_B≥ F_B,α to hipotezę H₀ odrzucamy (istotny wpływ czynnika B)

Jeżeli zachodzi F_A < F_A,α lub F_B < F_B,α to nie udowodniono istotnego wpływu danego czynnika.

P

Koszty materiałowe pewnego wyrobu produkowanego trzema różnymi metodami (technologiami) w czterech różnych zakładach, mają rozkład normalny o jednakowej wariancji. Losowe obserwacje tych kosztów dały następujące wyniki (w zł):

Zakłady / Metody	I	II	III
1	25	30	23
2	20	40	18
3	30	40	20
4	25	50	27

Na poziomie istotności α=0,05 zweryfikować hipotezę o braku wpływu metod produkcji oraz zakładów produkcyjnych na poziom kosztów materiałowych wyrobu.

Wpływ metod produkcji oraz zakładów produkcyjnych na poziom kosztów zostanie wykazany, gdy odrzucimy statystyczną hipotezę H₀, że średnie wartości m_ij kosztów są równe dla i=1,2,3,4 (zakłady) oraz j=1,2,3 (metody produkcji). Hipotezę tę zweryfikujemy testem analizy wariancji dla klasyfikacji podwójnej. Przyjmijmy jako pierwszy czynnik A, według którego klasyfikujemy obserwacje kosztów, rodzaj zakładu produkcyjnego. Drugim czynnikiem klasyfikacyjnym B, niech będzie rodzaj metody (technologii) produkcji.

Dla r=4, k=3 mamy:

_x_1.=78/3=26

_x_2.=78/3=26

_x_3.=90/3=30

_x_4.=102/3=34

_x_.1=100/4=25

_x_.2=160/4=40

_x_.3=88/4=22

_x=348/12=29

SKc=1040

SK_A=3*44=132

SK_B=4*186=744

SK_R=1040-132-744=164

Żródło zmienności	Suma kwadratów	Stopnie swobody	Wariancja	Test F
czynnik A (zakłady)	132	3	44	FA=44/27,33=1,61
czynnik B (metody)	744	2	372	FB=372/27,33=13,61
resztowa (błąd losowy)	164	6	27,33

Z tablicy rozkłady F Snedecora dla przyjętego poziomuy istotności idla liczby stopni swobody 3 i 6 odczytujemy krytyczną wartość F_A,α=4,76. Natomiast dla liczby stopni swobody 2 i6 odczytujemy wartość F_B,α=5,14

Ponieważ F_A=1,61<4,76=F_A,α zatem nie ma istotnego wpływu czynnika A, tj. zakładów produkujących na poziom kosztów.

Natomiast F_B=13,61>5,14=F_B,α zatem wpływ czynnika B (metodaa produkcji) okazał się statystycznie istotny na poziom kosztów materiałowych wyrobu. Grupowanie kosztów ze względu na metodę produkcji jest więc konieczne, gdyż typ technologii zmienia poziom badanych kosztów materiałowych.

Z

Przeprowadzono doświadczenie w celu stwierdzenia wpływu sposobów uprawy (pionowo) oraz nawożenia (poziomo) na plon ziemniaków.

Z

W celu sprawdzenia efektów różnych rodzajów paliwa rakietowego wystrzelono z trzch różnych wyrzutni rakiety z róznymi paliwami.

Z

W celu zbadania wpływu różnych receptur sporządzania betonu i różnego surowca na wytrzymałość betonu przeprowadzono eksperyment.

NIEPARAMETRYCZNE TESTY ISTOTNOŚCI

Test zgodności χ²

Nieparametryczne testy istotności, w których weryfikowana hipoteza dotycząca rozkładu badanej cechy nie precyzuje wartości parametrów rozkładu. Testy te można podzielić na dwie grupy: testy zgodności i testy dla hipotezy, że dwie próby pochodzą z jednej populacji (czyli że dwie populacje mają ten sam rozkład).

Test zgodności χ² pozwala na sprawdzenie hipotezy, że populacja ma określony typ rozkładu (tj. określoną postać funkcyjną dystrybuanty). Może to być typ rozkładu skokowego lub ciągłego. Jedynym ograniczeniem w teście zgodności χ² jest to, że próba musi być duża, bo wyniki jej dzielimy na pewne klasy wartości.

Dla każdej klasy z rozkładu hipotetycznego oblicza się liczebności teoretyczne, które porównuje się z empirycznymi za pomocą odpowiedniej statystyki χ² . Gdy rozbieżności między liczebnościami empirycznymi a teoretycznymi są zbyt duże, hipoteza, że populacja ma właśnie ten rozkład teoretyczny, musi być odrzucona.

Najczęściej zachodzi potrzeba sprawdzenia, czy populacja ma rozkład normalny.

Należy pamiętać, że klasy, na jakie dzieli się wyniki próby, w tym teście, nie powinny być zbyt mało liczne, tak by do każdej klasy wpadało co najmniej 8 wyników próby.

Model

Populacja generalna m dowolny rozkład o dystrybuancie należącej do pewnego zbioru Ω rozkładów o określonym typie postaci funkcyjnej dystrybuanty. Z populacji tej wylosowano niezależnie dużą próbę (n co najmniej kilkadziesiąt), której wyniki podzielono na r rozłącznych klas o liczebnościach n_i w każdej klasie, przy czym n=∑n_i Otrzymano w ten sposób tzw. rozkład empiryczny. Na podstawie wyników tej próby należy sprawdzić hipotezę,H₀, że populacja generalna ma rozkład typu Ω, tzn. H₀: F(x)∈ Ω, gdzie F(x) jest dystrybuantą rozkładu populacji.

Test istotności, zwany testem zgodności, dla tej hipotezy jest następujący.

Z hipotetycznego rozkładu typu Ω obliczamy dla każdej z r klas wartości badanej cechy X prawdopodobieństwa p_i, że zmienna losowa X o rozkładzie Ω przyjmie wartości należące do klasy o numerze i (i=1,2,...,r). Z kolei mnożąc p_i przez liczebność całej próby n otrzymuje się liczebności teoretyczne np_i, które powinny były wystąpić w klasie i, gdyby populacja miała rozkład typu Ω, tzn. gdyby hipoteza H₀ była prawdziwa. Ze wszystkich liczebności empirycznych n_i oraz hipotetycznych np_i wyznacza się następnie wartość statystyki

r (n_i - np_i )²

χ² = ∑ -----------------------

i=1 np_i

która przy założeniu prawdziwości hipotezy H₀ ma rozkład asymptotyczny χ² o r-1 stopniach swobody lub o r-k-1 stopniach swobody, gdy z próby szacowano k parametrów rozkładu Ω metodą największej wiarygodności.

Obszar krytyczny w tym teście buduje się prawostronnie w oparciu o rozkład χ² , tzn. odczytuje się taką wartość krytyczną χ_α² by zachodziło

P{χ² ≥ χ_α² }=α

Jeśli zachodzi nierówność χ² ≥ χ_α² to hipotezę o rozkładzie należy odrzucić.

W przeciwnym przypadku, tzn. gdy χ² <χ_α² nie ma podstaw do odrzucenia hipotezy H₀, że rozkład populacji jest typu Ω. Oczywiście nie oznacza to, że możemy ją przyjąć, lecz test χ² jest tak zbudowany, że im jest bliższa zeru wartość χ² , tym hipoteza H₀ jest bardziej wiarygodna.

Gdy w rozkładzie empirycznym z próby występuje w pewnej klasie liczebność mniejsza od 8, to należy połączyć ją z sąsiednią, uzyskując większą liczebność.

P1

Losowa próba n=200 niezależnych obserwacji miesięcznych wydatków na żywność 3-osobowych dała następujący rozkład tych wydatków (w tys. zł)

Wydatki	Liczba rodzin
1,0-1,4	15
1,4-1,8	45
1,8-2,2	70
2,2-2,6	50
2,6-3,0	20

Na poziomie istotności α=0,05 zweryfikować hipotezę, że rozkład wydatków na żywność jest normalny.

Stawiamy hipotezę H₀:F(x)∈ Ω, gdzie Ω jest klasą wszystkich dystrybuant normalnych.

Hipotezę weryfikujemy za pomocą testu χ² . Dwa parametry rozkładu, średnią m i odchylenie standardowe σ, szacujemy z próby za pomocą estymatorów uzyskanych metodą największej wiarygodności i uzyskujemy wartości _x=2,0 tys. zł oraz s=0,43 tys. zł

Niech u_i oznacza standaryzowaną wartość prawego końca przedziału klasowego (u_i=(x_i-_x)/s), a F(u_i) wartość dystrybuanty rozkładu N(0,1) w punkcie u_i.

xi	ni	ui	F(ui)	pi	npi	(ni - npi)^2	(ni-npi)^2 /npi
1,4	15	-1,39	0,082	0,082	16,4	1,96	0,12
1,8	45	-0,46	0,323	0,241	48,2	10,24	0,21
2,2	70	+0,46	0,677	0,354	70,8	0,64	0,01
2,6	50	1,39	0,918	0,241	48,2	3,24	0,07
3,0	20	-	-	0,082	16,4	12,96	0,79
	200			1,000	200,0		1,20

Prawdopodobieństwo dla ostatniego przedziału wyznaczamy jako 1-F(1,39). Otrzymaliśmy wartość statystyki χ² =1,2

Dla 5-2-1=2 stopni swobody z tablicy rozkładu χ² di dla α=0,05 mamy χ_α² =5,991

χ² =1,20 < 5,991 = χ_α²

nie ma podstaw do odrzucenia hipotezy H₀, że rozkład miesięcznych wydatków na żywność w populacji rodzin 3osobowych jest normalny.

Test zgodności λ Kołmogorowa

Podczas gdy w teście χ² dla zweryfikowania hipotezy, że populacja ma określony typ rozkładu, rozpatruje się liczebności szeregu empirycznego i porównuje się je z liczebnościami szeregu hipotetycznego, to w teście λ Kołmogorowa porównuje się dystrybuantę empiryczną i hipotetyczną. Jeśli bowiem populacja generalna ma rozkład zgodny z hipotezą, to wartości dystrybuanty empirycznej i hipotetycznej powinny być we wszystkich badanych punktach zbliżone. Punktem wyjście w teście λ jest analizowanie bezwzględnych wartości różnic między tymi dwoma dystrybuantami. Największa różnica służy do budowy statystyki λ, której rozkład niezależny od postaci dystrybuanty hipotetycznej, podał Kołmogorow.. Rozkład ten służy do budowy obszaru krytycznego w omawianym teście, przy czym jeżeli maksymalna różnica w pewnym punkcie obszaru zmienności badanej cechy jest zbyt duża, to hipotezę, że rozkład populacji ma taką dystrybuantę jak przypuszczamy, należy odrzucić.

W praktyce korzysta się z granicznego rozkładu, tzn. z dużej próby. Grupując duża próbę w klasy należy to czynić tak, by nie były one zbyt szerokie (tzn. powinno ich być dużo)

Podstawowym wymogiem stosowalności testu λ jest, by dystrybuanta hipotetyczna była ciągła. Do badania zgodności z rozkładem skokowym używać więc należy testy χ² nie λ

Z testem zgodności λ Kołmogorowa wiąże się test Kołmogorowa-Smirnowa dla weryfikacji hipotezy, że dwie próby pochodzą z tej samej populacji, tzn. że dwie populacje mają ten sam rozkład.

Model I

Populacja generalna ma rozkład ciągły o dystrybuancie F(x). Z populacji wylosowano niezależnie do próby n elementów (n co najmniej kilkadziesiąt). Na podstawie wyników tej próby należy zweryfikować hipotezę H₀: F(x)=F₀(x), gdzie F₀(x) jest konkretną, hipotetyczną i ciągłą dystrybuantą.

Wyniki próby porządkujemy w kolejności rosnącej lub grupujemy je w stosunkowo wąskie przeziały, o prawych końcach x_j i odpowiadających im liczebnościach n_j. Wyznaczamy dla każdego x_j wartośc tzw. empirycznej dystrybuanty F_n(x) według wzoru

n_sk

F_n(x_k)=---------------

n

gdzie n_sk oznacza skumulowaną od początku aż do x_k liczebność tj.

n_sk=∑ n_j

_{j≤ k}

Z rozkładu hipotycznego wyznaczamy dla każdego x_j wartość teoretycznej dystrybuanty F(x). Obliczamy dla każdego x_j bezwzględną wartość różnicy F_n(x)-F(x), tj. dystrybuanty empirycznej i teoretycznej.

Z kolei obliczamy wartość statystyki

D=sup | F_n(x)-F(x)| ; sup to wartość najmniejsza z szeregu

_x

oraz wartość statystyki

λ=D√ n

która przy prawdziwości hipotezy H₀ ma rozkład λ Kołmogorowa, niezależny od postaci hipotetycznej dystrybuanty F(x).

Dla ustalonego poziomu istotności α odczytujemy następnie z granicznego rozkładu λ Kołmogorowa taką wartość krytyczną λ_α, aby zachodziło

P{λ≥ λ_α}=α a następnie porównujemy wartość empiryczną λ z krytyczną wartością λ_α. Jeżeli zajdzie nierówność λ<λ_α nie ma podstaw do odrzucenia hipotezy H₀, że rozkład badanej cechy ma dystrybuantę hipotetyczną F(x).

Model II

Dane są dwie populacje generalne o rozkładach z ciągłymi dystrybuantami F₁(x) i F₂(x). Z populacji tej pobrano losowo dwie duże próby o liczebności n₁ i n₂. Na podstawie wyników tych prób należy sprawdzić hipotezę, że obie próby pochodzą z tej samej populacji, tzn. hipotezę H₀:F₁(x)=F₂(x)

Test istotności Smirnowa oparty na statystyce λ jest następujący.

Wyniki obu prób grupujemy w stosunkowo wąskie przedziały klasowe o tych samych końcach x_j. Dla każdego x_j obliczamy wartości empirycznych dystrybuant z obu prób

F_n1(x)= (n_1sk)/n₁ F_n2 (x)=(n_2sk)/n₂

Obliczamy następnie

D=sup|F_n1(x) - F_n2(x)|

oraz

λ=D√ n gdzie n=(n₁ * n₂)/ (n₁ + n₂)

Z tablicy tego rozkładu dla poziomu istotności α odczytujemy wartość krytyczną λ_α, tak by

P{λ≥ λ_α}=α

Gdy obliczona wartość statystyki λ spełnia nierówność λ≥ λ_α hipotezę H₀ odrzucamy.

P1

Na pewnej maszynie toczy się wiertła o określonej średnicy. Losowa próba n=200 dała następujący rozkład średnic (w mm) wyprodukowanych wierteł.

Średnica	Liczba wierteł
29,5-30,5	12
30,5-31,5	23
31,5-32,5	35
32,5-33,5	62
33,5-34,5	44
34,5-35,5	18
35,5-36,5	6

Na poziomie istotności α=0,05 zweryfikować za pomocą testu Kołmogorowa hipotezę, że rozkład średnic wierteł jest normalny.

Typ zadania zgodny zmodelem I.

Weryfikujemy hipotezę H₀:F(x)=F₀(x), gdzie F₀(x) jest dystrybuantą rozkładu N(m,σ). Z próby obliczamy oszacowania obu parametrów rozkładu normalnego, otrzymując _x=32,9 i s=1,4.

Ze względu na dużą próbę przyjmujemy te wartości za m i α.

xj	uj	F(uj) = F(x)	nj	nsk	Fn(x)	| Fn(x)-F(x)|
30,5	-1,71	0,044	12	12	0,060	0,016
31,5	-1,00	0,159	23	35	0,175	0,016
32,5	-0,29	0,386	35	70	0,350	0,036
33,5	+0,43	0,666	62	132	0,660	0,006
34,5	1,14	0,873	44	176	0,880	0,007
35,5	1,86	0,969	18	194	0,970	0,001
36,5	2,57	0,995	6	200	1,000	0,005

Otrzymaliśmy zatem D=0,036. Ponieważ √ n=√ 200=14,14, wartość empiryczna statystyki λ Kołmogorowa wynosi zatem

λ=0,036*14,14=0,509

Z tablicy rozkładu λ Kołmogorowa (granicznego) odczytujemy dla przyjętego poziomu istotności α=0,05 wartość krytyczną λ_α=1,358

Ponieważ rozkład λ Kołmogorowa jest dystrybuantą więc dla α=0,05 przy prawostronnym obszarze krytycznym należy szukać λ dla Q(λ)=0,95!

Ponieważ λ=0,509 < 1,358=λ_α więc nie ma podstaw do odrzucenia hipotezy H₀, że rozkład średnic wierteł jest normalny.

P2

W dwu grupach uczniów wylosowanych ze szkół wiejskich oraz miejskich otrzymano następujące rozkłady pojemności życiowej płuc tych uczniów (w cm3)

Pojemność życiowa płuc	Liczba uczniów szkół miejskich	Liczba uczniów szkół wiejskich
3100-3200	2	-
3200-3300	8	-
3300-3400	12	5
3400-3500	15	10
3500-3600	20	14
3600-3700	24	20
3700-3800	21	26
3800-3900	17	34
3900-4000	13	27
4000-4100	10	22
4100-4200	5	18
4200-4300	3	12
4300-4400	-	8
4400-4500	-	4

Na poziomie istotności α=0,01 zweryfikować za pomocą testu Kołmogorowa-Smirnowa hipotezę, że rozkłady pojemności życiowej płuc są identyczne u uczniów szkół miejskich i wiejskich.

Weryfikujemy hipotezę H₀: F₁(x)=F₂(x), że dystrybuanty obu rozkładów są identyczne.

n₁=150 n₂=200

xj	n1j	n2j	n1sk	n2sk	Fn1(x)	Fn2(x)	| Fn1(x) - Fn2(x)|
3100-3200	2	-	2	0	0,013	0	0,013
3200-3300	8	-	10	0	0,067	0	0,067
3300-3400	12	5	22	5	0,147	0,025	0,122
3400-3500	15	10	37	15	0,247	0,075	0,172
3500-3600	20	14	57	29	0,380	0,145	0,235
3600-3700	24	20	81	49	0,540	0,245	0,295
3700-3800	21	26	102	75	0,680	0,375	0,305
3800-3900	17	34	119	109	0,793	0,545	0,248
3900-4000	13	27	132	136	0,880	0,680	0,200
4000-4100	10	22	142	158	0,947	0,790	0,157
4100-4200	5	18	147	176	0,980	0,880	0,100
4200-4300	3	12	150	188	1,000	0,940	0,060
4300-4400	-	8	150	196	1,000	0,980	0,020
4400-4500	-	4	150	200	1,000	1,000	0

D*=0,305

n=(150*200)/(150+200)=30000/350 =85,7

√ n=9,26

λ=0,305*9,26=2,824

λ_α =1,627

λ=2,824 >1,627=λ_α

zatem hipotezę H₀ trzeba odrzucić. Nie można twierdzić, że pojemność życiowa płuc uczniów ma taki sam rozkład w populacji uczniów wiejskich i miejskich.

Z

Na podstawie danych liczbowych zweryfikować hipotezę, że ilość zapamiętanych przez dzieci elementów w teście psychologicznym ma rozkład normalny.

Test niezależności χ²

Przy badaniu populacji generalnej jednocześnie ze względu na dwie cechy interesuje nas sprawdzenie hipotezy, czy cechy te są ze sobą związane. Gdy obie cechy są mierzalny posługujemy się wtedy pojęciem korelacji i regresji. Gdy przynajmniej jedna z dwu badanych cech jest niemierzalna (tzn. ma jedynie kategorie jakościowe), to posługujemy się pojęciem niezależności stochastycznej zmiennych losowych. Zmienne te są niezależne, gdy dla dystrybuant zachodzi równość F(x,y)=F₁(x)F₂(x)

Wymogiem tego testu jest duża liczebność próby, której wyniki zostały rozdzielone na odpowiednie grupy wartości (kategorie), ze względu na obie cechy od razu. Sporządza się zatem odpowiednią tablicę kombinowaną dla dwu cech, zwaną tablicą niezależności, która po wypełnieniu daje macierz liczebności empirycznych. Nakłada się na nią macierz liczebności teoretycznych, obliczonych przy założeniu niezależności cech znajdujących się w główce i w boczku. Porównanie elementów obu macierzy, czego dokonuje się przez zastosowanie statystyki χ² , daje odpowiedź czy można odrzucić hipotezę o niezależności cech na skutek wystąpienia zbyt dużych różnic liczebności empirycznych i teoretycznych.

Model

Populacja generalna jest równocześnie badana ze względu na dwie cechy, niekoniecznie mierzalne. Z populacji tej wylosowano niezależnie próbę o liczebności n elementów. Wyniki próby klasyfikujemy w kombinowaną tablicę niezależności o r wierszach i s kolumnach. W boczku tablicy jest r grup wartości (kategorii) cechy X, a w główce tablicy jest s grup wartości (kategorii) cechy Y. Wnętrze tablicy wypełniają liczebności n_ij (i=1,...,r, j=1,...,s), oznaczające, ile elementów w próbie miało wartości obu cech należących do kombinacji (i,j). Podział na kategorie obu cech powinien być taki, by n_ij ≥ 8 Sumując wiersze i kolumny otrzymanej z próby macierzy liczebności empirycznych [n_ij] otrzymujemy liczebności brzegowe, które wygodnie jest oznaczyć jako n_i oraz n._j

Zachodzą równości

n_i = ∑ n_ij (j=1 do s) n._j= ∑ nij (i=1 do r)

n= ∑ dla (i=1 do r) ∑ n_ij (j=1 do s) = ∑ n_i (i=1 do r) = ∑ n._j (j=1 do s)

Na podstawie ułożonych w tablicę wyników próby należy sprawdzić hipotezę, że badane cechy są niezależne, tzn. hipotezę H₀: P{X=x_i , Y=y_j}= P(X=x_i) * P(Y=y_j) gdzie x_i oraz y_j oznaczają odpowiednie wartości lub kategorie badanych cech.

Z liczebności brzegowych tablicy niezależności szacujemy prawdopodobieństwo brzegowe

p_i = n_i / n p,_j = n._j / n

Następnie, zakładając prawdziwość hipotezy H₀ tzn. niezależność cech, obliczamy dla każdej kratki tablicy prawdopodobieństwa hipotetyczne

r s

p_ij = p_i * p._j przy czym ∑ ∑ p_ij=1

i=1 j=1

Mnożąc te prawdopodobieństwa przez ogólną liczebność próby otrzymujemy macierz liczebności teoretycznych [np_ij] Z elementów macierzy liczebności empirycznych [n_ij] oraz elementów macierzy liczebności teoretycznych [np_ij} konstruujemy statystykę.

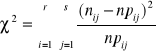
Statystyka ta ma przy założeniu prawdziwości hipotezy H₀ o niezależności cech, asymptotyczny rozkład χ² z (r-1)(s-1) stopniami swobody.

Obszar krytyczny (prawostronny) w tym teście określa nierówność χ² ≥ χ_α² , gdzie χ_α² jest wartością krytyczną odczytaną z tablicy rozkładu χ² dla ustalonego z góry poziomu istotności α i dla (r-1)(s-1) stopni swobody, w taki sposób, aby zachodziła relacja P(χ² >χ_α² )=α

Obliczoną wartość χ² porównujemy z wartością krytyczną χ_α² i jeśli zajdzie nierówność, to hipotezę H₀ o niezależności badanych cech należy odrzucić.

Uwaga.

Ze względu na wymaganą liczebność co najmniej 8 elementów w każdej kratce, zachodzi czasem konieczność połączenia za pomocą spójnika „lub” dwu kategorii danej cechy w jedną. Zmniejszają się przy tym wymiary tablicy niezależności, a co za tym idzie, zmniejsza się liczba stopni swobody statystyki χ² . Najmniejsze wymiary tablicy niezależności wynoszą 2x2 i statystyka χ² ma wtedy tylko jeden stopień swobody (jest to tzw. tablica czteropolowa)

P

W celu stwierdzenia, czy podanie chorym na pewną chorobę nowego leku przynosi poprawę w ich stanie zdrowia, wylosowano dwie grupy pacjentów w jednakowym stopniu chorych na tę chorobę i jednej grupie o liczebności 120 podawano nowy lek, a druga grupa o liczebności 80 pacjentów otrzymywała tradycyjne leki. Po pewnym czasie stwierdzono zestawione w tablicy liczebności chorych w poszczególnych kategoriach stanu zdrowia. Na poziomie istotności α=0,001 zweryfikować hipotezę, że nowy lek istotnie poprawia stan zdrowia pacjentów.

Leczeni	Stan zdrowia po leczeniu
		Bez poprawy	wyraźna poprawa	całkowite wyzdrowienie
badanym lekiem	20	40	60
tradycyjnie	45	20	15

Wysuniętą hipotezę badawczą zmieniamy na hipotezę statystyczną

H_0: P(X=x_i, Y=y_j) = P(X=x_i) P(Y=y_j)

o niezależności obu badanych cech jakościowych (tj. rodzaju leczenia i stanu zdrowia po leczeniu). Jeżeli powyższą hipotezę statystyczną H₀ o niezależności w wyniku zastosowania testu niezależności χ² trzeba będzie odrzucić, to oznaczać to będzie wobec danych zawartych w powyższej tablicy, że stan zdrowia po leczeniu zależy istotnie od zastosowania badanego leku, co udowodniłoby jego przydatność.

Obliczenia w teście χ² niezależności rozpoczynamy od obliczeń liczebności brzegowych n_i i p._j. Przyjmując następnie o niezależności cech obliczamy prawdopodobieństwa teoretyczne p_ij=p_i * p._j. Wyniki obliczeń prawdopodobieństw p_ij zamieszczamy w prawym górnym rogu każdej kratki. Mnożąc te prawdopodobieństwa przez n=200 otrrzymujemy dla każdej kratki liczebności teoretyczne np_ij, które umieszczamy w dolnym lewym rogu.

Trzeba zauważyć, że ze względu na konieczność bilansowania się elementów w wierszach i kolumnach obliczenia przeprowadzamy tylko dla tylu kratek, ile wynosi liczba stopni swobody, tzn. (r-1)(s-1)=(2-1((3-1)=2, a pozostałe elementy zarówno macierzy [p_ij] jak i [np_ij] wyznaczamy z wartości brzegowych.

Leczeni	Stan zdrowia po leczeniu
		bez poprawy	wyraźna poprawa	całkowite wyzdrowienie	ni.	pi.
badanym lekiem	0,195 20 39	0,180 40 36	0,225 60 45	120	0,60
tradycyjnie	0,130 45 26	0,120 20 24	0,150 15 30	80	0,40
n.j	65	60	75	200
p.j	0,325	0,300	0,375		1,00

następnie sporządzamy tabelę do obliczenia wartości statystyki χ²

nij	npij	(nij - npij)^2	(nij - npij)^2 / npij
20	39	361	9,26
40	36	16	0,44
60	45	225	5,00
45	26	361	13,88
20	24	16	0,67
15	30	225	7,50
200	200		36,75

χ² =36,75

Dla α=0,001 i dla (r-1)(s-1)=2 stopni swobody wartość krytyczna χ_α² =13,815

χ² =36,75 > 13,815=χ_α²

znaleźliśmy się w obszarze krytycznym, zatem hipotezę H₀ odrzucamy. Oznacza to, że podawanie pacjentom nowego leku w sposób istotny poprawia ich stan zdrowia.

Z

Pewien produkt można wytwarzać 3 metodami produkcji. Wysunięto hipotezę, że wadliwość produkcji nie zlaeży od metody produkcji.

Jakość	Metoda produkcji
		I	II	III
dobra	40	80	60
zła	10	60	20

Zweryfikować hipotezę o niezależnośc jakości produkcji od metod produkcji.

Z

W celu zweryfikowania hipotezy, że studentki zdają lepiej egzaminy niż studenci, wylosowano próbę i otrzymano wynika zaliczenia letniej sesji egzaminacyjnej

Sesja	Studentki	Studenci
zaliczona	75	25
niezaliczona	55	25

sprawdzić hipotezę o niezależności wyników egzaminacyjnych od płci.

W ankiecie rozesłanej wśród pracowników pewnego resortu pytano czy chcieliby zmienić obecne miejsce pracy.

Zarobek w zł	Odpowiedź
		tak	nie
1000-1500	46	62
1500-2000	94	146
2000-2500	249	501
2500-3000	126	326
3000-3500	43	135
4000-4500	26	70

Zweryfikować hipotezę, że chęć zmiany miejsca pracy nie zależy od wysokości zarobków.

Z

W celu sprawdzenia hipotezy, że plony żyta zależą od rodzaju gospodarstwa (PGR, spółdzielnie, gosp. indywidualne) wylosowano próby.

plony żyta PGR Spłdz indyw.

Z

W celu sprawdzenia hipotezy, że młodzież męska noszące długie włosy ma gorsze wyniki w nauce, wylosowano próbę 492 uczniów i otrzymano następujące dane.

Młodzież męska	Wyniki w nauce
		złe	dobre
ma modną fryzurę	51	43
nie ma	195	203

Zweryfikować hipotezę o niezależności wyników w nauce od fryzury młodzieży męskiej.

Testy serii

Testy te służą sprawdzeniu hipotezy, że dwie populacje mają ten sam rozkład (tj. dwie próby pochodzą z jednej populacji). Zastępują one najczęściej test parametryczny dla dwóch średnich, kiedy nie można przyjąć założeń stosowalności takiego testu.

Testy nieparametryczne mają mniejszą moc od testów parametrycznych, ale górują nad nimi prostotą budowy i rachunków. Są one wszystkie testami istotności, tj. pozwalają jedynie na odrzucenie sprawdzanej hipotezy, ale nie wymagają prawie żadnych krępujących założeń o populacji. Należy wszakże uciekać się do tych testów tylko, gdy nie można zastosować testów parametrycznych.

Serią nazywamy każdy podciąg złożony z kolejnych elementów jednego rodzaju utworzony w ciągu uporządkowanych w dowolny sposób elementów dwu rodzajów. Gdy elementy danego ciągu są losowe, wtedy zarówno długość serii jak i ilość serii utworzona w danym ciągu są zmiennymi losowymi. Znajomość rozkładów tych zmiennych pozwala na zbudowanie prostych testów istotności dla różnych hipotez. Testy niżej omówione oparte są na rozkładzie zmiennej losowej będącej liczbą utworzonych serii w badanym ciągu.

omówione:

test losowości próby

test dla hipotezy, że dwie próby pochodzą z jednej populacji

test dla hipotezy o liniowej postaci funkcji regresji

Model I

Dana jest populacja generalna o dowolnym rozkładzie. Z populacji tej pobrano w pewien określony sposób próbę n elementów. Należy sprawdzić hipotezę, że jest to próba losowa, tzn. że sposób doboru elementów można uznać za losowy.

Z uporządkowanego według kolejności pobierania elementów do próby ciągu wyników próby obliczamy medianę me z próby. Każdemu wynikowi próby x_i w tym uporządkowanym chronologicznie ciągu przypisujemy symbol a, jeżeli x_i<me bądź symbol b, jeżeli x_i>me. Wynik x_i=me można odrzucić. Otrzymujemy w ten sposób zamiast chronologicznego ciągu wartości x_i ciąg złożony z symboli a i b, np. abbaaaabbbbabaab. W ciągu tym otrzymujemy pewną liczbę serii (tutaj np. 8). Oznaczamy przez k statystykę oznaczającą liczbę serii.

Przy założeniu prawdziwości hipotezy o losowości próby, liczba serii k ma znany i stablicowany rozkład zależny tylko od n₁ i n₂ liczebności elementów a i b. Tablice rozkładu liczby serii podają taką wartość k_α, że P{k≤ k_α}=α, W oparciu o ten rozkład budujemy dwustronny obszar krytyczny dla testu losowości w taki sposób, że dla przyjętego poziomu istotności α (najczęściej 0,05) odczytujemy z tablic takie dwie wartości krytyczne k₁ i k₂, aby zachodziły relacje:

P(k≤ k₁}=1/2 * α i P{k≤ k₂}=1- (1/2 *α)

Odczytaną z danego ciągu liczbę serii k porównujemy z tymi wartościami krytycznymi k₁ i k₂. Jeżeli zajdzie jedna z nierówności k≤ k₁ lub k≥ k₂ to hipotezę o losowości próby należy odrzucić. Otrzymaliśmy zbyt małą lub zbyt dużą liczbę serii. Natomiast gdy zajdzie nierówność k₁ < k < k₂ nie ma podstaw do odrzucenia hipotezy o losowości próby.

Model II

Dane są 2 populacje generalne o dowolnych rozkładach badanej cechy. Z populacji tych wylosowano dwie próby o liczebnościach odpowiednio n₁ i n₂. Na podstawie wyników tych prób należy zweryfikować hipotezę, że rozkłady obu populacji nie różnią się, czyli H₀: dwie próby pochodzą z jednej populacji.

Wyniki obu prób ustawiamy w jeden ciąg według rosnących wartości. Oznaczamy elementy próby z jednej populacji za pomocą symbolu a, a zdrugiej populacji za pomocą symbolu b. Odczytujemy z niemalejącego ciągu liczbę serii k. Obszar krytyczny budujemy lewostronnie w taki sposób, że z rozkładu liczby serii odczytujemy dla odpowiednich n₁ i n₂ oraz dla ustalonego z góry poziomu istotności α taką wartość krytyczną k_α, by P(k≤ k_α}=α.

Jeżeli otrzymamy liczbę serii k z danego ciągu, która spełnia nierówność k≤ k_α to hipotezę H₀ odrzucamy, tzn. dwie próby różnią się istotnie. Jeżeli natomiast k>k_α to nie ma podstaw do odrzucenia hipotezy, że rozkłady obu populacji są takie same, czyli dwie próby nie różnią się istotnie.

Model III

Daną populację generalną badamy ze względu na dwie cechy X i Y. Z populacji tej wylosowano n elementów do próby, otrzymując wyniki (x_i, y_i). Na podstawie wyników tej próby należy zweryfikować hipotezę, że funkcja regresji cechy Y względem X w populacji jest liniowa, tzn. jest w postaci y=αx + β

Z wyników próby, metodą najmniejszych kwadratów, wyznaczamy oszacowanie funkcji (^)y=ax+b oraz jej wartość y_i (^) dla wszystkich x_i w próbie. Wartości y_i z próby odpowiadające uporządkowanym według kolejności rosnącej wartościom x_i oznaczamy symbolem a, jeżeli y_i>y_i(^) (tj. punkt empiryczny leży ponad prostą regresji), bądź symbolem b, gdy y_i<y_i(^) (punkt empiryczny leży poniżej prostej). W uprządkowanym według rosnących wartości x_i ciągu wyników próby odczytujemy liczbę serii k. Z tablic liczby serii odczytujemy na n₁ i n₂ liczbę elementów a i b oraz dla ustalonego z góry poziomu istotności α taką wartość krytyczną k_α, że P(k≤ k_α)=α.

Jeżeli zajdzie nierówność k≤ k_α to hipotezę o liniowym charakterze funkcji regresji Y względem X należy odrzucić; oznacza to, że wykres funkcji regresji jest jakąś krzywą.

gdy zaś k>k_α to nie ma podstaw do odrzucenia hipotezy, bo liczba serii jest duża, co oznacza, że przeprowadzona prosta zostawia po obu stronach punkty empirycznie dobrze do nich pasując. Z uwagi na własności metody najmniejszych kwadratów, najmniejsza liczba serii wynosi k=3.

P1

Do pewnych doświadczeń farmakologicznych potrzebne są szczury o określonej wadze ciała. Po otwarciu klatki do próby wzięto pierwszych 15 zwierząt, które same wyszły z klatki. Były to zwierzęta o następujących kolejnych wagach (w g): 530, 620, 560. 320, 480, 550, 490, 500, 460, 430. 380, 390, 360, 400, 370. Za pomocą testu serii na poziomie istotności α=0,10 zweryfikować hipotezę, że taki dobór zwierząt do próby jest losowy.

Typ zadania zgodny z modelem I.

Ponieważ n=15 więc mediana jest ósmy w kolejności rosnącej wynikiem. me=460.

Oznaczając symbolem a wyniki w ciągu podstawowym mniejsze od mediany, a b wyniki większe uzyskujemy ciąg

bbbabbbb aaaaaa, w którym liczba serii wynosi k=4. Liczba elementów a wynosi n₁=7, liczba elementów b wynosi n₂=7.

Z tablicy rozkładu liczby serii dla α=0,10, tj. dla 1/2α=0,05 i 1-1/2α=0,95 odczytujemy wartości krytyczne k₁=4 i k₂=11.

Ponieważ z ciągu otrzymaliśmy k=4, zatem hipotezę należy odrzucić (k=k₁). Oznacza to, że otrzymaliśmy zbyt małą ilość serii, by można było uznać próbę za losową.

P2

Wylosowano z dwu klas po 6 dzieci i otrzymano dla dzieci z klasy A następujące wyniki badania inteligencji (tzw. iloraz inteligencji): 110,112,115,98,130,123, a dla dzieci z klasy B wyniki:88,135,140,138,95,125. Za pomocą testu serii na poziomie istotności α=0,05 zweryfikować hipotezę, że te dwie próby pochodzą z jednej populacji dzieci o określonym rozkładzie ilorazu inteligencji.

Typ zadania modelu II.

W celu uzyskania jednego ciągu łączymy wyniki obu prób i ustawiamy je w kolejności rosnącej. Otrzymamy ciąg 88,95,98,110,112,115,123,125,130,135,138,140. Oznaczając symbolem a wyniki uczniów z klasy A, a symbolem b wyniki ucznioów klasy B, otrzymujemy dla powyższego ciągu ciąg symboli: bbaaaaababbb, w którym liczba serii wynosi k=5. Odczytana z liczby tablicy seri dla lewostronnego obszaru krytycznego wartość krytyczna k_α przy α=0,05 oraz n₁=6 i n₂=6 wynosi k_α=3

Ponieważ k=5 > 3=k_α więc nie ma podstaw do odrzucenia hipotezy, że obie próby pochodzą z jednej populacji, tzn. nie róznią się istotnie pod względem poziomu ilorazu inteligencji.

P3

Badając zależność między dwoma wymiarami pewnego metalowego odlewu otrzymano z próby o liczebności n=12 następujące wyniki (w mm)

xi	16	20	22	24	33	47	55	70	77	82	90	94
yi	25	34	60	83	92	104	110	124	133	150	145	170

Przypuszczamy, że funkcja regresji wymiaru X i Y jest liniową funkcją w postaci y=2x+5. Na poziomie istotności α=0,05 zweryfikować hipotezę o liniowości funkcji regresji.

Porównując wartości funkcji regresji y_i(^) z empirycznymi wartościami y_i dla kolejnych, rosnących wartości x_i z próby otrzymujemy następujący ciąg utworzony z symboli a (gdy punkt leży ponad prostą) oraz z symbolu b (gdy punkt leży poniżej prostej)

bbaaaabbbbbb

Liczba serii w tym ciągu wynosi k=3. Dla n₁=4 i n₂=8 oraz dla α=0,05 odczytujemy dla lewostronnego obszaru krytycznego, wartość krytyczną k_α=3

k=3=k_α, co oznacza, że hipotezę o liniowości funkcji regresji należy odrzucić.

Z

Zbiór jabłek w sadzie pewnego gospodarza w dziesięcioleciu w kolejnych latach był następujący (w q): {....} Na poziomie istotności α=0,10 zweryfikować hipotezę, że jest to próba losowa (tzn. że nie ma cyklicznosci w zbiorze).

Z

W pewnym doświadczeniu farmakologicznym z podawaniem dwu różnych preparatów badano potęgowanie narkozy u myszy. Na poziomie istotnośc α zweryfikować hipotezę, że oba preparaty w jednakowym stopniu przedłużają czas narkozy u myszy.

Test znaków

Bardzo prostym testem nieparametrycznym dla hipotezy, że dwie próby pochodzą z jednej populacji jest test znaków. Nie wymaga on bowiem żadnych operacji rachunkowych, a rozkład populacji może być przy tym dowolny, byle ciągły. Jedynym założeniem jest to, by wyniki porównywanych dwu jednakowo liczebnych prób stanowiły pary odpowiadających sobie wzajemnie liczb.

Test znaków ma najczęściej zastosowanie przy badaniu, czy populacja generalna nie ulega zmianie w czasie (parę stanowią wyniki badania elementu w dwu kolejnych momentach), bądź też przy porównywaniu jakiegoś elementu przed eksperymentem naukowym i po jego przeprowadzeniu.

Statystyką, której rozkład służy do budowy obszaru krytycznego, jest liczba znaków (minus lub plus) różnic wyników stanowiących pary. Rozkład liczby znaków jest rozkładem dwumianowym, został dla wygody stablicowany, przy czym w tablicach podaje się taką liczbę znaków r_α, że P{r≤ r_α }=α, Jeżeli więc w omawianym teście przez r oznaczy się liczbę tych znaków, których w próbie uzyskano mniej, to można wykorzystać bezpośrednio do budowy lewostronnego obszaru krytycznego dla tej liczby znaków.

Model

Dane są dwie populacje generalne o ciągłych dystrybuantach F₁(x) i F₂(x). Z populacji tych wylosowano jednakową liczbę parami odpowiadających sobie n elementów. Na podstawie wyników tych prób należy sprawdzić hipotezę, że obie próby pochodzą z tej samej populacji, tzn. hipotezę H₀:F₁(x)=F₂(x).

Test istotności dla tej hipotezy, zwany testem znaków, jest następujący.

Badamy znak różnicy par wyników w obu próbach i znajdujemy liczbę tych znaków, których jest mniej. Oznaczamy tę liczbę przez r. Zmienna losowa r, przy prawdziwości hipotezy H₀, ma rozkład dwumianowy. Nie powinniśmy otrzymać liczby r zbyt małej. Z tablicy rozkładu liczby znaków odczytujemy dla ustalonego z góry poziomu istotności α i dla liczby par wyników n taką wartość r_α, że P(r≤ r_α}=α. Otrzymaną w próbie liczbę r tych znaków, których jest mniej, porównujemy z wartością krytyczną r_α,. Jeżeli zajdzie nierówność r≤ r_α to hipotezę H₀ odrzucamy, tzn. dwie próby pochodzą z różnych rozkładów, jeżeli natomiast zajdzie nierówność r>r_α, to nie ma podstaw do odrzucenia hipotezy H₀, że obie próby pochodzą z jednej populacji.

Gdyby jakaś para w próbie miała identyczne wyniki, to nie bierzemy jej pod uwagę.

P

W celu stwierdzenia, czy szkolenie zawodowe zwiększa wydajność pracy robotników, wylosowano w pewnych zakładzie próbę n=14 pracowników i zbadano ich średnią wydajność pracy przed i po przeszkoleniu zawodowym. Otrzymano wyniki (ilość sztuk wyprodukowanych na godzinę)

Przed szkoleniem	52	220	125	84	150	92	94	125	78	265	187	113	63	146
Po szkoleniu	66	242	120	107	159	80	115	162	90	241	197	101	85	180

Za pomocą testu znaków na poziomie istotności α=0,10 zweryfikować hipotezę, że wydajność pracy przed szkoleniem i po szkoleniu jest taka sama.

Oznaczając przez + (plus) wzrost wydajności pracy, a przez - (minus) jej spadek, otrzymujemy ciąg znaków + + - + + - + + + - + - + +. Liczba znaków minus wynosi r=4. Z tablicy liczby znaków dla α=0,10 i n=14 odczytujemy wartość krytyczną r_α=3. Ponieważ r=4>3=r_α, więc nie ma podstaw do odrzucenia hipotezy o jednakowej wydajności pracy przed i szkoleniem i po szkoleniu. Oznacza to, że ta próba nie udowodniła poprawy wydajności pracy robotników po szkoleniu zawodowym.

Z

W celu sprawdzenia, czy pewien lek obniża ciśnienie krwi u chorych na nadciśnienie, wylosowano n pacjentów i zmierzono im ciśnienie przed podaniem tego leku i w pewnym czasie po podaniu. Na poziomie istotności α zweryfikować hipotezę, że obie próby pochodzą z jednej populacji.

Z

Wysunięto hipotezę, że ceny artykułów żywnościowych uległy w pewnym okresie czasu podwyżce. W celu sprawdzenia tej hipotezy wylosowano n rodzajów artykułów żywnościowych stwierdzając, że ceny ich na początku i na końcu badanego okresu były następujące. Na poziomie istotności α zweryfikować hipotezę, że ceny artykułów żywnościowych nie uległy zmianie w ciągu badanego okresu.

Z

Na podstawie danych liczbowych zweryfikować hipotezę na poziomie istotności α,, że trening pamięci zwiększa liczbę zapamiętanych przez uczniów elementów.

Omówiony test znaków nie jest testem precyzyjnym, gdyż wykorzystuje on jedynie znak róznicy wyników tworzących parę w dwu próbach.

Test rangowanych znaków

Test rangowanych znaków uwzględnia wielkość danej różnicy dodatniej lub ujemnej. Istotą tego testu jest rangowanie, tj. nadanie kolejnych numerów, według rosnących wartości róznic dodatnich oraz ujemnych branych oddzielnie.

Test rangowanych znaków pozwala na sprawdzenie hipotezy, czy dwie próby, których wyniki są wzajemnie sobie przyporządkowane pochodzą z jednej populacji, czy nie. Rozkład może być dowolny, byle ciągły.

Model

Dane są dwie populacje generalne o ciągłych dystrybuantach F₁(x) i F₂(x). Z populacji tych wylosowano jednakową liczbę n elementów do dwu prób, których wyniki odpowiadają sobie parami. Na podstawie wyników tych prób należy zweryfikować hipotezę, że obie próby pochodzą z tej samej populacji, tzn. hipotezę H₀: F₁(x)=F₂(x).

Obliczamy różnice wyników obu prób dla wszystkich par wyników. Rangujemy wartości bezwzględne tych różnic (tzn. nadajemy im kolejne numery poczynając od 1 dla namniejszej co do wartości bezwzględnej różnicy). Wyznaczone rangi piszemy w dwu grupach, oddzielnie dla różnic dodatnich oraz ujemnych. Sumując rangi w tych dwu grupach, uzyskujemy sumę rang T⁺ dla różnic dodatnich i sumę rang T^- dla różnic ujemnych. Znajdujemy wartość statystyki T, jako mniejszą z tych dwu sum rang, tzn.

T=min{T⁺, T^-}

Statystyka T ma przy założeniu prawdziwości hipotezy H₀, znany rozkład. Tablice tego rozkładu podają dla ustalonego prawdopodobieństwa α i dla liczby par n takie wartości T_α, że zachodzi P{T≤ T_α}=α. Ponieważ tablice te są trudno dostępne, podajemy poniżej wartości T_α dla dwu prawdopodobieństw α=0,05 i α=0,01

Rozkład zmiennej T rangowanych znaków

n	α=0,05	α=0,01
8	4	0
9	6	2
10	8	3
11	11	5
12	14	7
13	17	10
14	21	13
15	25	16
16	30	20
17	35	23
18	40	28
19	46	32
20	52	38
21	59	43
22	66	49
23	73	55
24	81	61
25	89	68

Gdy n>25 można korzystać z granicznego rozkładu normalnego, bo statystyka T ma rozkład asymptotycznie zbliżony do N(m, σ), gdzie m=(1/4)*n*(n+1), σ=√ [(1/24)*n*(n+1)*(2n=1)]

Lewostronny obszar krytyczny w omawianym teście istotności określony jest przez nierówność T≤ T_α. Oznacza to, że gdy porównując obliczoną wartość T z wartością krytyczną T_α otrzymamy nierówność T≤ T_α wtedy hipotezę H₀ odrzucamy. Natomiast gdy zajdzie nierówność T>T_α nie ma podstaw do odrzucenia hipotezy H₀, że obie próby pochodzą z jednej populacji.

Jeżeli przy rangowaniu różnic występują jednakowe wartości tych różnic, to nadajemy każdej z nich rangę (numer) będącą średnią arytmetyczną rang, jakie kolejno te różnice otrzymałyby, gdyby nie były jednakowe.

P

W przykładzie z poprzedniego paragrafu zamieszczono dane dotyczące zbadania wydajności pracy przed i po szkoleniu zawodowym.

Przed szkoleniem	52	220	125	84	150	92	94	125	78	265	187	113	63	146
Po szkoleniu	66	242	120	107	159	80	115	162	90	241	197	101	85	180

Za pomocą testu rangowanych znaków zweryfikować na poziomie istotności α=0,05 hipotezę, że wydajność pracy przed szkoleniem i po szkoleniu jest taka sama.

R.

Stawiamy hipotezę, że obie próby pochodzą z jednej populacji. Ponieważ wyniki obu prób stanowią pary liczb (x_i, y_i), można zweryfikować hipotezę za pomocą testu rangowanych znaków.

x_i oznacza wynik przed szkoleniem, y_i - wynik po szkoleniu. R_i oznacza rangę różnicy.

yi - xi	Ri+	Ri-
16	7
22	9,5
-5		1
23	11
9	2
-12		5
21	8
37	14
12	5
-24		12
10	3
-12		5
22	9,5
34	13
	82,0	23

Otrzymaliśmy zatem T+=82 oraz T-=23. Zatem T=23

Dla ustalonego poziomu istotności α=0,05 i dla n=14 otrzymujemy z tablicy wartość krytyczną T_α=21. Ponieważ T=23>21=T_α zatem nie ma podstaw do odrzucenia hipotezy, że wydajność pracy przed i po szkoleniu zawodowym jest taka sama.

Nie zawsze wynik przy zastosowaniu dwu różnych testów do tego samego zadania jest taki sam. Wtedy należy uznać za właściwy wynik uzyskany za pomocą testu o większej precyzji, wykorzystującym więcej informacji zawartych w próbie.

Z

Zweryfikować hipotezę, że zmiana technologii produkcji obniżyła czas wykonywania pewnego detalu. (Zweryfikować hipotezę, że czas wykonywania tego detalu jest jednakowy przez i po zmianie technologii produkcji.

Test mediany

Czasami sprawdzając hipotezę, że dwie próby pochodzą z jednej populacji, nie mamy przyporządkowania wynikom jednej próby wyników drugiej próby. Wówczas, oprócz wyżej opisanego już testu serii, możemy użyć, gdy próba nie jest zbyt mała, prostego innego testu - testu mediany.

Istotą tego testu jest wyznaczenie mediany ze wszystkich wyników obu prób, a następnie policzenie, ile wyników z każdej próby znalazło się poniżej, a ile powyżej mediany. Jeżeli testowana hipoteza jest prawdziwa, to w obu próbach powinna być taka sama część wyników poniżej oraz powyżej mediany. Uzyskane liczebności zestawia się w czteropolową tablicę niezależności i oblicza wartość statystyki χ² tak samo, jak w teście niezależności χ². Statystyka χ² w teście mediany ma jeden stopień swobody. W teście tym nie zakłada się nic na temat rozkładu populacji, ,można zatem go stosować zamiast testu dla dwu średnich, dla dowolnych populacji.

Model

Dane są dwie populacje generalne o rozkładach z dowolnymi dystrybuantami F₁(x) i F₂(x). Z populacji tych pobrano losowo dwie próby o liczebnościach odpowiednio n₁ i n₂ elementów (n₁ i n₂ są niezbyt małe). Na podstawie wyników tych prób należy sprawdzić hipotezę, że obie próby pochodzą z jednej populacji, tzn. H₀: F₁(x)=F₂(x)

Z wyników obu prób tworzymy jeden ciąg niemalejący, ustawiając wyniki w kolejności rosnące. Z ciągu tego wyznaczamy medianę me. Grupujemy wszystkie obserwacje w tablicę czteropolową:

Wyniki	Próba 1	Próba 2
> me	...	...
≤ me	...	...

We wnętrzu tablicy znajdują się liczebności obserwacji z obu prób w liczbie n₁+n₂. Traktujemy tę tablicę tak, jak tablicę niezależności, i obliczamy z niej wartość statystyki

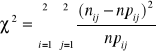
Jeżeli hipotez H₀ jest prawdziwa, to statystyka ta ma asymptotyczny rozkład χ² z jednym stopniem swobody. Z tablicy rozkładu χ² odczytujemy wartość krytyczną χ_α² tak, by P(χ² ≥ χ_α² )=α. Następnie porównujemy wartość χ² z wartością krytyczną χ_α² . Jeżeli zachodzi nierówność χ² ≥ χ_α² to hipotezę H₀ odrzucamy.

P

W dwu przedsiębiorstwach budowlanych sporządzono według tego samego przepisu próbki betonu. W przedsiębiorstwie A otrzymano następujące wyniki badania wytrzymałości na ściskanie (w kG/cm² ): 190, 206, 206, 210, 212, 189, 198, 205, 216, 190, 199, 200, 175, 224, 219, 205, 200, 213, 180, 176, 196, 204, 219, 196, 208, 212

natomiast w przedsiębiorstwie B: 202, 209, 186, 195, 225, 240, 215, 174, 195, 201, 193, 217, 201, 188, 181, 203, 229, 233, 185, 195, 211, 231, 217, 229, 225, 229, 220, 217, 209, 194

Na poziomie istotności α=0,05 za pomocą testu mediany zweryfikować hipotezę, że oba przedsiębiorstwa wykonały beton o tej samej wytrzymałości.

W celu zastosowania testu mediany należy utworzyć jeden ciąg niemalejący i z niego wyznaczyć medianę me. Otrzymujemy

174, 175, 176, 180, 181, 185, 186, 188, 189, 190, 190, 193, 194, 195, 195, 195, 196, 196, 198, 199, 200, 200, 201, 201, 202, 203, 204, 205, 205, 206, 206, 208, 209, 209, 210, 211, 212, 212, 213, 215, 216, 217. 217, 217, 219, 219, 220, 224, 225, 225, 229, 229, 229, 231, 233, 240

Ponieważ ilość elementów wynosi 26+30=56 zatem mediana wynosi me=1/2 *(x₂₈+x₂₉)=205

Grupujemy teraz obserwacje w tablicę czteropolową:

Wyniki	Przedsiębiorstwo A	Przedsiębiorstwo B	ni	pi
> 205	0,224 11 13	0,258 16 14	27	0,482
≤ 205	0,240 15 13	0,278 14 16	29	0,518
n.j	26	30	56
p.j	0,464	0,536		1,00

nij	npij	(nij - npij)^2	(nij - npij)^2 / npij
11	13	4	0,308
16	14	4	0,286
15	13	4	0,308
14	16	4	0,250
			1,152

χ² =1,152

χ_α² =3,841

χ² =1,152 < χ_α² =3,841 nie ma więc podstaw do odrzucenia hipotezy, że wykonany beton w obu przedsiębiorstwach ma taką samą wytrzymałość (że obie próby pochodzą z tej samej populacji)

Z.

Zbadano zawartość wody w jabłkach dwu gatunków. Zweryfikować hipotezę, że oba gatunki jabłek mają ten sam procent zawartości wody.

Z

Na podstawie danych liczbowych zweryfikować hipotezę, że czas snu pacjentów chorych na dwie rózne choroby A i B jest jednakowy.

Test sumy rang

Test sumy rang jest jednym z najwygodniejszych a jednocześnie dość precyzyjnych testów nieparametrycznych dla wielu prób. Nie zakłada się w nim o rozkładach nic oprócz ciągłości.

Test ten do pewnego stopnia zastępuje test analizy wariancji dla średnich.

W teście tym istotą jest nadanie kolejnych numerów (rang) wszystkim wynikom w kilku próbach i obliczenie sumy tych rang dla każdej próby oddzielnie. Jeżeli sprawdzana hipoteza, że wszystkie próby pochodzą z jednej populacji, jest prawdziwa, to sumy rang dla poszczególnych prób nie powinny zbyt dużo różnić się od siebie.

Statystyka ma rozkład graniczny χ² z k-1 stopniami swobody, gdzie k jest liczbą porównywanych prób. Gdy liczebność poszczególnych prób nie jest zbyt mała, to można z rozkładu χ² wyznaczyć prawostronny obszar krytyczny dla tego testu.

Model

Danych jest k populacji generalnych o dowolnych rozkładach z ciągłymi dystrybuantami F₁(x), F₂(x), ..., F_k(x). Z każdej z tych populacji wylosowano niezależnie n_i elementów do próby (i=1, 2, ..., k). Na podstawie wyników tych prób należy sprawdzić hipotezę, że wszystkie próby pochodzą z jednej populacji, tzn. hipotezę H₀:F₁(x)=F₂(x)=...=F_k(x)

Test istotności, zwany testem sumy rang, jest dla tej hipotezy następujący.

Wszystkim wynikom prób w liczbie n=∑n_i nadajemy rangi (numery kolejne) od 1 do n( przy jednakowych wynikach, dajemy średnią z mających kolejno nastąpić rang). Dla każdej próby oddzielnie wyznaczamy sumy rang T_i (i=1,2, ...,k). Z tych sum rang wyznaczamy wartość statystyki

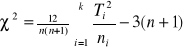
Jeżeli hipoteza H₀ jest prawdziwa, to statystyka ta ma asymptotyczny rozkład χ² o k-1 stopniach swobody. Z tablicy rozkładu χ² dla przyjętego z góry poziomu istotności α i dla k-1 stopni swobody odczytujemy wartość krytyczną χ² , tak by zachodziło P{χ² ≥ χ_α² }=α. Jeżeli spełniona jest nierówność χ² ≥ χ_α² to hipotezę H₀ trzeba odrzucić, w przeciwnym wypadku nie ma podstaw do odrzucenia hipotezy H₀, że wszystkie próby pochodzą z jednej populacji.

P

Z trzech zakładów produkujących telewizory wylosowano odpowiendnio liczby n₁ =10, n₂=8, n₃=12 sztuk i otrzymano następujące wyniki dotyczące badania czułości (w mikrowoltach) tych odbiorników

Zakład
A	B	C
420	400	450
560	420	700
600	580	630
490	470	590
550	470	420
570	500	590
340	520	610
480	530	540
510		740
460		690
		540
		670

Na poziomie istotności α=0,05 za pomocą testu sumy rang zweryfikować hipotezę, że czułość telewizorów produkowanych przez wszystkie zakłady jest jednakowa.

Ogólna liczebność wszystkich prób wynosi

n=n₁+n₂+n₃=10+8+12=30

Nadajemy wszystkim wynikom, od najmniejszego do największego, kolejno rangi od 1 do 30, a następnie sumujemy je dla każdej próby oddzielnie, otrzymując sumy rang T₁, T₂, T₃

Zakład
A		B		C
wynik	ranga	wynik	ranga	wynik	ranga
420	4	400	2	450	6
560	19	420	4	700	29
600	24	580	21	630	26
490	11	470	8,5	590	22,5
550	18	470	8,5	420	4
570	20	500	12	590	22,5
340	1	520	14	610	25
480	10	530	15	540	16,5
510	13			740	30
460	7			690	28
				540	16,5
				670	27
	127		85		253

Otrzymaliśmy T₁=127, T₂=85, T₃=253. Z kolei wyznaczamy wartość statystyki χ² przy czym n=30

χ² =12/(30*31) * (127² /10 + 85² /8 + 253² /12) -3*31 =8,29

χ_α² =5,991.

χ² =8,29>5,991=χ_α² więc hipotezę H₀, że próby pochodzą z jednej populacji trzeba odrzucić. Oznacza to, że wyprodukowane przez zakłady A, B, C telewizory mają różną czułość.

Z

W doświadczeniu chemicznym wyznacza się 3 metodami ciepło spalania gatunku węgla. Sprawdzić hipotezę, że wszystkie trzy metody dają jednakowe wyniki pomiarów.

Z

Na podstawie danych liczbowych zweryfikować hipotezę, że wszystkie trzy kombinacje nawozowe dają na poletkach doświadczalnych jednakowe plony badanej odmiany pszenicy.

ANALIZA REGRESJI I KORELACJI

---