Lekcja 7. Gry dwuosobowe o sumie zero. Czysty i mieszany strategii. Gry statystyczne.

7.1. Podstawowe pojęcia teorii gier.

7.2. Gry macierzowe o sumie zero.

7.3. Czyste i mieszane strategii. Metoda Brown'a przybliżonego rozwiązania zadań teorii gier.

7.4. Zadania teorii gier a zadania planowania liniowego.

7.5. Gry statystyczne. Kryterium powzięciu decyzji.

7.1. Podstawowe pojęcia teorii gier.

W zadaniach ekonomicznych można wyróżnić zadania podejmowania decyzji w warunkach niepewności. Przykładami takich zadań mogą być zadania podejmowania decyzji w przedsiębiorstwie, gdzie mamy do czynienia z sytuacjami, w których nie wiadomo, jaki będzie stan naszego otoczenia lub też, jaką decyzje podejmie nasz konkurent na rynku, od czego będą zależeć wyniki decyzji podejmowanych przez nas. W podobnej sytuacji znajduje się rolnik podejmujący decyzję o wyborze materiału siewnego, nie znający przyszłorocznej pogody, ilości opadów, cen na giełdach zbożowych itp.

W nieco innej sytuacji znajdować się będą dwaj gracze w szachy (niepewna przyszłość, doskonale znana przeszłość, decyzje podejmowane jedna po drugiej). Wreszcie mamy i takie sytuacje, w których uczestniczą więcej niż dwie osoby, znana jest przeszłość, a informacja o przyszłości, o możliwościach podejmowania decyzji jest ograniczona.

Przedstawione tu sytuacje w pewnym sensie klasyfikują problematykę podejmowania decyzji w warunkach niepewności, a w szczególności problematykę teorii gier.

Teoria gier to jest rozdział badań operacyjnych, który zajmuje się opracowaniem metod podejmowania decyzji w warunkach sytuacji konfliktowych i warunkach niepewności.

Ogólnie biorąc, matematyczna teoria gier może byé stosowana do opisu i badania wszystkich tych problemów zarządzania, które rozwiązywane są w sytuacjach niepewnych i konfliktowych, np. badanie popytu, prognozowanie, optymalizacja jakości produkcji, określanie wielkości zapasów, ocena prawdopodobieństwa bezawaryjnej pracy linii technologicznej, wybór optymalnego wariantu cyklu inwestycyjnego, motywacja personelu, i wiele innych. Teoria gier jest działem matematyki badającym problemy typowe dla gier strategicznych, tj. gier, o których wyniku decyduje nie tylko przypadek, ale również umiejętności występujących stron (graczy). Gry strategiczne stanowią matematyczne modele sytuacji konfliktowych, w których występujące strony (gracze) dążą do rozbieżnych celów. Każdy taki model matematyczny określa kto i w jaki sposób jest zainteresowany w określonym wyniku konfliktu (w wygranej). Formalizując matematycznie sytuacji konfliktowe, można przedstawić te sytuacji jako grę dwóch, trzech lub więcej graczy, prześladujących celi maksymalizacji swojej wygranej kosztem innego gracza.

Zbiór reguł definiujących jednoznacznie kolejność działalności jednej ze stron (jednego z graczy) w sytuacji konfliktowej nazywa się strategią.

„Grą” nazywa się zbiór omówionych wcześniej graczami reguł i warunków.

Jeśli n gracze G₁, G₂, ... , G_n, przejmują udział w grze, wtedy podstawowe zadanie teorii gier brzmi: jak powinien postępować gracz z numerem j (j=1, 2, ... , n) dla osiągnięcia swojego celu - maksymalizacji wygranej?

Przepuśćmy dalej, że w końcu gry każdy gracz G_j otrzymuje kwotę v_j, którą nazywamy wygranej w tej grze. Jeżeli v_j >0, to gra jest wygrana graczem G_j, jeśli v_j <0, to przegranej graczem G_j , a jeśli v_j = 0 , to gra skończyła się remisem.

W dużej ilości przypadków mamy gry o sumie zero: v₁ + v₂ + ... + v_n = 0. W takich grach suma wygranej przechodzi od jednego gracza do drugiego, bez wykorzystania zewnętrznych źródeł.

Przykładami gier o sumie zero mogą być zadania ekonomiczne. W takich zadaniach suma wygranej jest stała, zmienia się tylko suma wygranej każdego gracza. W przeciwnym przypadku mamy grę o sumie niezerowej.

W grze może brać udział dwóch lub więcej graczy lub koalicji.

Poniżej rozważamy:

— gry dwuosobowe o sumie zero, w tym tzw. gry z naturą,

— gry dwuosobowe o sumie dowolnej, niekooperacyjne i kooperacyjne,

— gry wieloosobowe, niekooperacyjne i kooperacyjne.

Podstawa matematycznej teorii gier jest schemat gry dwuosobowej z sumą zero. Jest to gra ściśle konkurencyjna, nie ma w niej miejsca na negocjacje między graczami — co jeden z nich wygrywa, co drugi przegrywa. Jeżeli w grze ściśle konkurencyjnej każdy z graczy dysponuje jedynie skończoną liczbą strategii, to nazywa się grą macierzową. Optymalne postępowanie obu graczy określone przez teorię gier ma charakter zasady stabilności: każdemu z graczy niewygodnie jest zmieniaé swoja strategie, jeżeli jego przeciwnik pozostawi swoją strategię nie zmieniona.

W grach dwuosobowych o sumie dowolnej wypłaty dla graczy określa się przy każdym podjęciu decyzji, przy czym interesy obu graczy nie są (nie musza być) dokładnie przeciwne, bardzo często obaj mogą nawet zyskać przez współpracą. Ponieważ zyski jednego gracza nie muszą być równe stratom drugiego, to wypłaty każdego z nich zapisujemy w osobnej macierzy (tablicy), skąd bierze się nazwa gry dwumacierzowe.

Rozróżnią się dwa rodzaje gier dwumacierzowych: 1) niekooperacyjne oraz 2) kooperacyjne.

W grach dwumacierzowych niekooperacyjnych jakiekolwiek porozumienie (np. skorelowane strategie czy wypłaty uboczne) jest zabronione.

W przypadku dwumacierzowych gier kooperacyjnych różnego rodzaju współpraca między obu graczami jest dozwolona. Można zawierać układy dopuszczające skorelowane strategie i przenoszenie wypłaty od jednego gracza do drugiego, chociaż nie zawsze liniowo (proporcjonalnie). W dwumacierzowych grach kooperacyjnych mamy do czynienia z problemami przetargu: jak wiele zechce dać jeden gracz drugiemu? jak mało zgodzi się przyjąć jako ceną za współpracą? Okazuje się, że można wyznaczyć pewną minimalną wartość kwoty, na którą gracz może się zgodzić.

Teoria wieloosobowych gier niekooperacyjnych niewiele różni się od teorii dwuosobowych gier niekooperacyjnych o sumie dowolnej. W przypadku wieloosobowych gier kooperacyjnych występuje pojęcie koalicji, która może powstać i utrzymać się przez pewien czas tylko pod warunkiem, że poszczególni jej członkowie powinni osiągnąć pewnego rodzaju równowagę lub stabilność. Teoria wieloosobowych gier kooperacyjnych analizuje więc pojęcie i warunki tej stabilności. Jest rzeczą intuicyjnie oczywista, że w takiej grze może istnieć bardzo wiele zbiorów stabilnych i wtedy nie wiadomo dokładnie, w jaki sposób dokonają wyboru jednego z nich.

7.2. Gry macierzowe o sumie zero.

Gry macierzowe o sumie zero są matematyczne najbardziej zbadane i mają duże zastosowanie w celach praktycznych.

Rozpatrzymy przykład.

Przykład 7.1. Rzucanie monety. Pierwszy gracz P wybiera jedną z dwóch stron monety. Drugi gracz D nie znając wyboru pierwszego, też wybiera jedną ze stron monety. Reguły gry są następujące: gracz D zapłaci 1 zł graczowi P, jeśli po jednoczesnym rzucaniu monet graczami P i D wypadli takie same stronę (orzeł-orzeł lub reszka-reszka), w przeciwnych przypadkach (orzeł-reszka lub reszka-orzeł) 1 zł płaci gracz P graczowi D (gracz P wygrywa (-1) zł). Przy takim przypuszczeniu mówimy, że gracz D gra na minimum, oraz gracz P - na maksimum.

Wtedy zadanie teorii gier możemy zapisać

Strategii graczy		D
				orzeł	reszka
P	orzeł	1	-1
		reszka	-1	1
1	-1
-1	1

Warunki gry zapisane przez macierz

wierszy której odpowiadają możliwym strategie dla gracza P, a kolumnę - strategie gracza D. Jeżeli gracz P wybiera wiersz, a D - kolumnę, gra będzie skończona i wygrana gracza P równa się wartości na przecięciu odpowiednich wiersza i kolumny.

W ogólnym przypadku gra macierzowa definiuje się przez prostokątną macierz wymiaru m x n. Numer i wiersza macierzy odpowiada numeru strategii A_i gracza P, oraz numer kolumny B_j odpowiada numeru strategii gracza D.

Tabela 7.1.

	B1	B2	...	Bn
A1	a11	a12	...	a1n
A2	a21	a22	...	a2n
...	...	...	...	...
Am	am1	am2	...	amn

Gra jednoznacznie będzie zapisana przez macierz

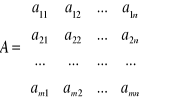
Elementy macierzy a_ij są wartości rzeczywiste i odpowiada sumie, wygranej przez graca P u gracza D, jeśli P wybiera strategie A_i, oraz D wybiera strategie B_j. Macierz A zwykle nazywa się macierzą wypłat.

Każdy gracz wybiera dla siebie najbardziej skuteczną strategie. Pierwszy gracz wybiera strategii, dążącą do maksymalizacji wygranej, drugi gracz wybiera strategii minimalizacji przegranej. Wtedy można wprowadzić pojęcie dolnej i górnej czystej ceną gry.

Dolną czystą ceną gry (maksyminem) nazywa się wartość

(7.1)

Górną czystą ceną gry (minimaksem) nazywa się wartość

(7.2)

Strategii graczy, odpowiadające maksyminu (minimaksu), nazywają się straregii maksyminowymi (minimaksowymi).

3	-3	4	6
3	8	7	4
5	1	4	8
4	6	2	9

Przykład 7.2. Znaleźć się strategii maksyminowe i minimaksowe w grze macierzowej:

Rozwiązanie. Zapiszemy grę w postaci macierzy wypłat.

Na podstawie (7.1) dla każdego wiersza znajdziemy najmniejszą wartość i zapiszemy w kolumnę a: (-3, 3, 1, 2).

	B1	B2	B3	B4	a
A1	3	-3	4	6	-3
A2	3	8	7	4	3
A3	5	1	4	8	1
A4	4	6	2	9	2
b	5	8	7	9

To oznacza, że dla dowolnej strategii gracza D najgorsza wygrana gracza P będzie odpowiednie (-3, 3, 1, 2). Z drugiej strony, gracz P powinien wybrać taką strategie (wiersz), żeby maksymalizować swoją wygraną. Wtedy

a = max(-3, 3, 1, 2) = 3

i strategią maksyminową dla gracza P będzie strategia A₂.

Analogicznie na podstawie (7.2) znajdziemy minimaksową strategie gracza D. Ponieważ gracz D wybiera strategii według kolumn, wtedy w najgorszym przypadku on może przegrać odpowiednie 5, 8, 7, 9. Dla minimalizacji przegranej gracz D wybiera strategię dla min(5, 7, 8, 9), tj. minmaksowi:

b = min(5, 7, 8, 9) = 5

Z macierzy wypłat widać, że strategią minimaksową gracza D będzie B₁.

Sytuacją równowagi a = b reprezentuje punkt siodłowy, utworzony przez pary strategii A_i i B_j odpowiednio graczy P i D, przy których osiągana jest relacja:

(7.3)

Lewa strona równania (7.3) określa maksymalną wygraną gracza P, która otrzyma on wybierając strategię A_i w najbardziej rozsądny sposób, natomiast prawa — minimalną przegrana gracza D, której nie może on w żaden sposób zapobiec (strategia B_j). Gdy gra ma punkt siodłowy, to obie wielkości są sobie równe (zasada minimaksu), a ich wartość nazywana jest czystą wartością gry.

W grach, które nie mają punktu siodłowego, maksimum po lewej stronie równania (7.3) jest mniejsze od minimum po jego prawej stronie. Zrównanie obu stron relacji (7.3) jest możliwe przez pewne rozszerzenie strategicznych możliwości obu graczy. Powinni oni wybierać swoje strategie nie deterministyczne, lecz losowo z określonymi prawdopodobieństwami, które zależą od funkcji wypłat (tzw. strategie mieszane).

7.3. Czysty i mieszany strategii. Metoda Brown'a rozwiązania zadań teorii gier.

Wyróżniają strategii czyste i mieszane. Czysta strategia A_i (i=1,2,...,m) pierwszego gracz P (czysta strategia B_j (j=1,2,...,n) drugiego gracza D) — są to możliwa strategia pierwszego (drugiego) gracza wybrana z prawdopodobieństwem p=1.

Jeśli pierwszy gracz ma m strategii, drugi — n strategii, wtedy dla dowolnej pary strategii pierwszego i drugiego gracza czyste strategii można przedstawić w postaci wektorów jednostkowych. Na przykład, dla strategii A_i i B_j czyste strategii możemy zapisać w postaci:

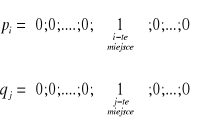
Twierdzenie 7.1. W gry macierzowej dolna czysta cena gry nie przekracza górnej czystej ceny gry, tj. a ≤ b.

Dowód. Z definicji
. Analogicznie,
. Łącząc dwie nierówności, otrzymujemy
. Stąd
i
, (i=1,2,...,m), (j=1,2,...,n). Ta nierówność jest prawidłowa dla dowolnych i i j, i wtedy
.

Jeśli dla strategii czystych A_i i B_j graczy P i D odpowiednie mamy równość a = b , to parę czystych strategii (A_i , B_j) nazywamy punktem siodłowym, element macierzy na przecięciu wiersza i i kolumny j - elementem siodłowym, a wartość v = a = b nazywana jest czystą wartością gry.

6	5	4	6
3	8	4	5
5	1	4	8
4	6	2	9

Przykład 7.3. Znaleźć dolną i górną czyste ceny gry, sprawdzić obecność punktów siodłowych.

Rozwiązanie. Zapiszemy grę w postaci macierzy wypłat.

Na podstawie (7.1) dla każdego wiersza znajdziemy najmniejszą wartość i zapiszemy w kolumnę a: (4, 3, 1, 2).

	B1	B2	B3	B4	a
A1	6	5	4	6	4
A2	3	8	4	5	3
A3	5	1	4	8	1
A4	4	6	2	9	2
b	6	8	4	9

a = max(4, 3, 1, 2) = 4 - dolna czysta cena gry,

i strategią maksyminową dla gracza P będzie strategia A₁.

Analogicznie na podstawie (7.2) znajdziemy minimaksową strategie gracza D.

b = min(6, 8, 4, 9) = 4 - górna czysta cena gry,

Z macierzy wypłat widać, że strategią minimaksową gracza D będzie B₃.

Ponieważ a = b = 4, wtedy mamy jeden punkt siodłowy (A₁ , B₃), a element siodłowy równa się 4.

Odchylenie gracza P od maksyminnej strategii A₁ prowadzi do zmniejszeniu wygranej, oraz odchylenie graca D od minimaksnej strategii B₃ spowoduje wzrost jego przegranej. Innym słowem, jeżeli w grze macierzowej występuje element siodłowy, wtedy optymalnymi dla graczy są ich strategii minimaksne.

Jeżeli gra macierzowa nie maje punktu siodłowego, wtedy a ≤ b i rozwiązanie gry jest skomplikowane. Wykorzystanie strategii minimaksowych powoduje, że dla każdego gracza wygrana jest nie większa niż a , a przegrana jest nie niższa niż b . Dla graczy powstaje pytanie zwiększenia wygranej (zmniejszenia przegranej). Rozwiązanie znajdziemy na podstawie strategii mieszanych.

Mieszaną strategią pierwszego (drugiego) gracza nazywa się wektor
, gdzie
i
(wektor
, gdzie
i
).

Wektor p (q) oznacza prawdopodobieństwo zastosowania i-ej czystej strategii pierwszym graczem (j-ej czystej strategii drugim graczem).

Ponieważ gracze wybierają swoje czyste strategii losowo i niezależnie od drugiego graczy, gra ma przypadkowy charakter i wielkość wygranej (przegranej) też będzie wartością losową. Wtedy średnia wartość wygranej (przegranej) — wartość oczekiwana — jest funkcją od mieszanych strategii р, q:

Funkcja f(р, q) nazywa się funkcją płac gry z macierzą { a_ij }.

Strategii
,
nazywają się optymalnymi, jeśli dla dowolnych strategii
,
są spełnione warunki

(7.4)

Wykorzystanie w grze optymalnych mieszanych strategii gwarantuje pierwszemu graczu wygraną nie mniejszą niż po zastosowaniu im innej dowolnej strategii р; drugiemu graczu — przegraną nie większą niż po wykorzystaniu im innej dowolnej strategii q.

Wartość funkcji płac dla optymalnych strategii jest ceną gry, tj.
.

Rozwiązaniem gry występuje zbiór optymalnych strategii i cena gry.

Twierdzenie 7.2. W mieszanych strategiach dowolna gra macierzowa z ograniczoną ilością kroków ma punkt siodłowy.

Niech mamy grą macierzową { a_ij } i niektóre mieszane strategii р*, q* gracze P i D z sumą wygranej v. Nas interesuje pytanie: jak sprawdzić, że zbiór (р*, q*, v) jest rozwiązaniem gry? Dla tego potrzebnie sprawdzić nierówność (7.4) dla dowolnych strategii mieszanych, pomiędzy których będą strategii р*, q*. Niestety, różnych mieszanych strategii istnieje nieskończona ilość. Wtedy sprawdzić nierówność (7.4) jest niemożliwe. Dla tego bez dowodu przyjmiemy twierdzenie.

Twierdzenie 7.3. Dla tego, żeby mieszane strategii
i
byli optymalne dla graczy P i D w grze z macierzą { a_ij } i wygranej v koniecznie i dostatecznie spełnienia nierówności:

(7.5)

(7.6)

Z twierdzenia 7.3 wynika, jeżeli spełnione są warunki (7.5), (7.6), wtedy jest spełniona nierówność (7.4), i mieszane strategii р* i q* — są optymalne.

Na podstawie twierdzenia 7.3 wnioskujemy:

- jeśli gracz P stosuje optymalną mieszaną strategię р*, a gracz D — inną czystą strategią В_j, wtedy wygrana gracza P będzie nie mniejsza od ceny gry v. Analogicznie,

- jeśli gracz D stosuje optymalną mieszaną strategię q*, a gracz P — inną czystą strategią A_i, wtedy przegrana gracza D będzie nie większa od ceny gry v.

Czyste strategii gracza wchodzące do jego optymalnej mieszanej strategii z prawdopodobieństwami nie równymi zero, nazywają się aktywnymi strategiami gracza.

Jest prawidłowe twierdzenie o aktywnych strategiach (bez dowodu).

Twierdzenie 7.4. Jeśli jeden z graczy wykorzystuje swoją optymalną mieszaną strategię, to jego wygrana zostanie niezmiennej i równa się cenie gry niezależnie od tego, jaką strategie stosuje inny gracz, jeżeli tylko on nie wychodzi za przedziały swoich aktywnych strategii.

Na podstawie twierdzenia 7.4. rozwiązanie gry macierzowej będzie uproszczono, jeśli wyjaśnić dominowanie jednych strategii nad innymi. Na przykład, rozpatrując strategii gracza P, porównujemy elementy wierszy s i t, mianowicie a_sj z elementami a_tj dla (j=1,2,...,n). Jeśli wszystkie a_sj ≥ a_tj (j=1,2,...,n), wtedy wygrana gracza P dla strategii A_s będzie większa, niż dla strategii A_t. Strategia A_s nazywa się dominującą, a strategia A_t. — dominowaną.

Ponieważ gracz D jest zainteresowany w minimalizacji przegranej, wtedy dominującej będzie kolumna z największymi elementami. Na przykład, rozpatrując strategii gracza D, porównujemy elementy kolumny k i r, mianowicie a_ik z elementami a_ir dla (i=1,2,...,m). Jeśli wszystkie a_ik ≥ a_ir (i=1,2,...,m), wtedy graczowi D wygodnie zrobić swój wybór na strategii B_r . Strategia B_r nazywa się dominującą, a strategia B_k — dominowaną.

Jeśli w grze macierzowej mamy wierszy (kolumny) z takimi samymi elementami, wtedy wierszy (kolumny), i odpowiednie strategii graczy P i D nazywają się dublowanymi.

W grze macierzowej dominowane i dublowane wierszy (kolumny) można wyeliminować bez wpływu na rozwiązanie gry.

Twierdzenie 7.5. Optymalne mieszane strategii р* i q* gracy P i D odpowiednie w grze macierzowej { a_ij } z ceną v będą optymalne w grze macierzowej { s*a_ij + g} z ceną s*v + g, gdzie s>0.

Dowód. Na podstawie twierdzenia 7.3 dla optymalnej mieszanej strategii р* gracza P i dla dowolnej czystej strategii B_j gracza D mamy

(7.7)

Pomnożymy obydwie części nierówności (7.7) na niektórą dodatnią wartość s > 0 i dodajemy do lewej i prawej części nierówności iloraz
. Otrzymujemy

(7.8)

Ponieważ
, z (7.8) otrzymujemy

(7.9)

gdzie cena gry v' = s*v + g

Zrobiony dowód twierdzenie dla optymalnej mieszanej strategii р* gracza P.

Analogiczne można zrobić dowód dla optymalnej mieszanej strategii gracza D.

Na podstawie twierdzenia 7.5 możemy przekształcić macierz płac z ujemnymi elementami w macierz z dodatnimi elementami.

-4	-2	5	1	2	7
1	2	4	3	0	10
3	5	6	7	1	9
1	2	4	3	0	10
2	1	3	6	5	4

Przykład 7.4. Uprościć grę macierzową

Rozwiązanie. Ponieważ elementy drugiego i czwartego wiersza są równe, tj. mamy dwa dublujących się wierszy. Wyeliminujemy, na przykład, czwarty wiersz.

Porównujemy elementy wierszy. Wszystkie elementy drugiego wierszu są mniejszy od odpowiednich elementów trzeciego wierszu. Wtedy strategia A₂ jest niewygodna graczowi P. Wyeliminujemy również drugi wiersz.

Porównujemy elementy kolumn. Elementy pierwszej kolumny są dominujące nad elementami trzeciej i szóstej kolumny (są najmniejszy). Wyeliminujemy 3-cią i 6-tą kolumnę. Analogicznie, elementy drugiej kolumny są dominujące nad elementami czwartej kolumny. Graczowi D jest niewygodnie wykorzystać strategii B₃, B₄, B₆.

-4	-2	2
3	5	1
2	1	5

Otrzymujemy uproszczoną macierz gry:

Jeżeli potrzebujemy macierz z dodatnimi elementami, wystarczy dodać do wszystkich elementów, na przykład, wartość +4.

Metoda Brown'a przybliżonego rozwiązania zadań teorii gier.

Metoda Brown'a polega na wzajemnym nauczaniu graczy. Każdy gracz, analizując sposób zachowania przeciwnika, stara się odpowiedzieć samym skutecznym sposobem.

Pierwszy gracz wybiera jedną ze swoich strategii. Drugi gracz odpowiada strategią, która minimalizuje wygraną pierwszego gracza. Każdy gracz odpowiada na kolejny krok przeciwnika taką strategią, która jest optymalna względem poprzednich kroków przeciwnika.

Przykład 7.5. Jako przykład rozpatrujemy rozwiązania gry z macierzą

2	0	9	6
1	3	6	0
4	2	1	3

Niech pierwszy gracz P wybiera strategię A₃ (trzeci wiersz macierzy). Drugi gracz D patrząc na trzeci wiersz wybiera element a₃₃=1 - najmniejszy element wiersza i zaznacza jego gwiazdką (*). Z prawej strony od macierzy wypisujemy elementy trzeciej kolumny (strategia B₃). Pierwszy gracz, znając decyzje drugiego i analizując zaznaczoną kolumnę, wybiera w nim największy element (zaznaczony gwiazdką) i wyznacza strategie A₁ . Drugim wierszem niżej macierzy zapisujemy skumulowaną wygraną pierwszego gracza za dwa kroki.

Minimalizując wygraną pierwszego gracza po dwóch krokach, drugi gracz wybiera strategię B₂ i tak dalej.

Częstość wyboru wierszy lub kolumny definiuje komponenty rozwiązania przybliżonego, elementy z gwiazdkami są skumulowana wygrana za t kroków.

Obliczenia w iteracyjnej metodzie Brown'a wygodnie prowadzić w podanej niżej tabeli. W lewym górnym kącie zapisana macierz gry. W wierszach niżej macierzy są obliczone skumulowana za n kroków wygrana pierwszego gracza. W kolumnach z prawej strony zapisana skumulowana za t kroków przegrana drugiego gracza.

Jeżeli po t krokach pierwszy gracz widzi, że jego przeciwnik wybiera czystą strategię B_j (suma gwiazdek w kolumnie j niżej macierzy gry) s_j razy (j=1,2,...,n), wtedy on może decydować że przeciwnik wykorzysta mieszaną strategię
. Na kolejnym kroku gry pierwszy gracz wybiera czystą strategię, która daje jemu maksymalną średnią wygraną przeciw y_t. Numer czystej strategii jest numerem maksymalnej wartości na t-tym kroku gracza drugiego (kolumna t z prawej strony).

Analogicznie, drugi gracz po t krokach przepuszcza, że optymalną strategią pierwszego gracza jest
, gdzie h_i jest ilość powtórzeń i -tej strategii (i=1,2,...,m) na poprzednich krokach. Na kolejnym t+1 kroku gry drugi gracz wybiera czystą strategię, która daje jemu minimalną średnią przegraną przeciw x_t. Numer czystej strategii jest numerem minimalnej wartości na t-tym kroku gracza pierwszego (wiersz t na dole).

Stopień przybliżenia do rozwiązania zależy od wyboru pierwszego kroku i od ilości kroków. Na przykład, dla

n=5

n=10

Tabela 7.2.

			Krok gracza 2		1	2	3	4	5	6	7	8	9	10
	2	0	9	6	9*	9	9	9	15	21*	23*	23*	23*	23
Krok gracza 1	1	3	6	0	6	9*	12*	15*	15*	15	16	19	22	25*
		4	2	1	3	1	3	5	7	10	13	17	19	21	23
					9	9	12	15	15	21	23	23	23	25
					max				1					5
1	4	2	1*	3	1	min			4					5
2	6	2*	10	9	2				0					0
3	7	5*	16	9	5
4	8	8*	22	9	8
5	9	11	28	9*	9	0	3	1	1
6	10	14	34	9*	9
7	12*	14	43	15	12
8	14	14*	52	21	14
9	16	14*	61	27	14
10	18	14*	70	33	14	1	6	1	2

7.4. Zadania teorii gier a zadania planowania liniowego.

Niech mamy grę rozmiarem m x n z macierzą { a_ij } :

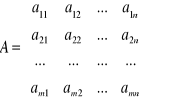
Zaznaczymy przez
i
optymalne mieszane strategii graczy P i D. Strategia р* gracza P gwarantuje jemu wygraną nie niższą niż v niezależnie od wyboru strategii B_j graczem D. Ten fakt możemy zapisać w postaci:

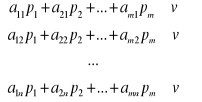
(7.10)

gdzie

Analogicznie, strategia q* gracza D gwarantuje jemu przegraną nie wyższą niż v niezależnie od wyboru strategii A_i graczem P. Ten fakt możemy zapisać w postaci:

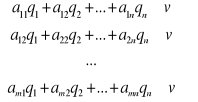
(7.11)

gdzie

Ponieważ elementy macierzy płac można zrobić dodatnimi na podstawie twierdzenia 7.5, wtedy cena gry v>0.

Przekształcimy układy (7.10), (7.11). Dla tego podzielmy nierówności na v>0 i wprowadzimy zaznaczenia
. Otrzymujemy:

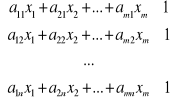
, (7.12)

gdzie

(7.13)

i

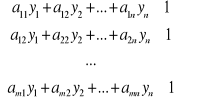
, (7.14)

gdzie

(7.15)

Ponieważ gracz P dąży do maksymalizacji ceny gry
, wtedy
będzie minimalizowana, i dla tego optymalna strategia gracza P będzie znaleziona z zadania PL postaci:

minimalizować funkcje
przy ograniczeniach (7.12), (7.13).

Optymalna mieszana strategia gracza D jest dualną do zadania PL dla gracza P. Zadanie PL dla gracza D brzmi:

maksymalizować funkcje
przy ograniczeniach (7.14), (7.15).

Rozwiązując parę dualnych zadań PL metodą simplex (lub graficznej dla dwóch zmiennych), znajdziemy:

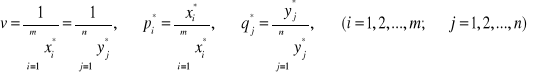
7.5. Gry statystyczne. Kryterium powzięcia decyzji.

Gry z naturą, zwane również grami statystycznymi, wywodzą się z teorii statystycznych funkcji decyzyjnych stworzonej przez A.Walda w latach pięćdziesiątych. Modele gier statystycznych dotyczą tzw. niepewnych sytuacji decyzyjnych, gdy na skutki decyzji wpływają parametry niepewne, o których nie mamy żadnych informacji na temat ich możliwych zmian. Klasyczny model dwuosobowej gry strategicznej o sumie zero (co jeden przeciwnik wygrał, to drugi przegrał) zostaí przez A.Walda rozszerzony na przypadek nieskończonej liczby strategii obu graczy. O naturze powiedziano, że — z definicji — nie jest zainteresowana rozgrywaną grą. Ponadto człowiekowi prowadzącemu grę z naturą zapewniono dodatkową informację o strategiach natury: „Ponieważ natura nie zmienia przez dłuższy czas tego losowego mechanizmu, według którego realizują się stany natury, statystyk może zdobyć pewne informacje o tym losowym mechanizmie, tzn. o rozkładzie prawdopodobieństw stanów natury". Podstawą pozostał jednak schemat dwuosobowej gry strategicznej z suma zero: gra jest ściśle konkurencyjna, nie ma w niej miejsca na negocjacje między graczami (co jeden przeciwnik wygra, drugi przegra).

W odróżnieniu od gry o sumie zero, gry z naturą rozgrywane są przy założeniu pasywnej postawy drugiego gracza. Założenie o pasywnej postawie drugiego gracza wymusza na nas zmianę reguł wyboru decyzji. Najpowszechniej stosowane są cztery przytoczone poniżej:

1. reguła maxmin (Walda),

2. Laplace'a (Bayesa),

3. Hurwicza,

4. Savage'a.

W pierwszym przypadku decyzje opierają się na regule analogicznej do reguły von Neumanna. Podejmujemy taką decyzję, przy której minimalna wygrana (ze względu na stan natury) dla decyzji wybranej przyjmie wartość największą, tzn. szukamy takiego A_i, dla którego:

(7.16)

Można powiedzieć, że jest to reguła asekurancka (wybór wartości najmniejszej — najmniejsza zapewniona wygrana), reguła gracza ostrożnego, ale inteligentnego (stąd poszukiwanie maksimum).

Reguła Laplace'a (Beyes'a) to reguła oparta na założeniu, że wszystkie przyszłe stany natury są jednakowo prawdopodobne (dla reguły Beyes'a są znane prawdopodobieństwa p_j stanów natury) i w związku z tym możliwe jest wyliczenie wartości oczekiwanej rezultatów każdej decyzji. Najlepsza będzie decyzja, dla której oczekiwana wygrana jest największa.

Można to zapisać w następujący sposób: znajdź takie A_i, dla którego:

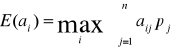
(7.17)

Oczywiście w tym przypadku preferowane będą takie decyzje, dla których suma wszystkich wygranych jest największa, a zatem mogą to być decyzje niekoniecznie najlepsze w sensie pierwszego kryterium.

Trzecim przytoczonym kryterium jest kryterium Hurwicza. Jest to kryterium, które łączy chęć zapewnienia sobie wygranej na możliwie wysokim poziomie z pewną skłonnością do podejmowania ryzyka.

Reguła Hurwicza polega na wyznaczeniu wielkości d, ze wzoru:

, (7.18)

gdzie
,
, γ oznacza współczynnik skłonności do ryzyka i przyjmuje wartości z przedziału [0, 1].

Decyzja optymalna w sensie kryterium Hurwicza określona zostanie przez wartość maksymalną wielkości d_i.

Wyznaczenia decyzji na podstawie reguły Savage'a dokonuje się w dwóch etapach. W pierwszym tworzymy macierz nazywaną „macierzą żalu". Macierz ta zdefiniowana jest w następujący sposób:

(7.19)

Następnie w tak określonej macierzy dla każdego wiersza poszukuje się elementu maksymalnego, a następnie wiersza, w którym wartość ta jest najmniejsza, tzn.:

(7.20)

Regułę tę można wyjaśnić w następujący sposób: dla każdego ze stanów natury z osobna, a następnie dla każdej możliwej decyzji wyznaczamy wielkość utraconych korzyści, które moglibyśmy osiągnąć (w stosunku do decyzji najlepszej przy danym stanie natury). Następnie postępujemy zgodnie z regułą von Neumanna, uwzględniając, że mamy do czynienia z wielkościami niepożądanymi, czyli wśród różnic w wierszu i wybieramy największą, a potem spośród nich najmniejszą. Wybrana wartość wskaże nam decyzję optymalną w sensie kryterium Savage'a.

Przykład 7.6. Bank może kupić na sumę b akcji А_i firmy z cenami a_i (i=1,2,3). Na koniec roku rynek papier wartościowych może być w jednym z dwóch możliwych stanów R₁ lub R₂. Eksperci ustalili, że dywidendy z jednej akcji z cenami a_i (i=1,2,3) firmy dla stanu rynku R_j na koniec roku mają wartości d_ij % od ceny. Potrzebnie:

1) zapisać zadanie w postaci gry, zbadać typ gry i gracze. Dla gracze wskazać możliwe strategii;

2) zapisać macierz płac;

3) zrobić rekomendacji dla banku w sprawie zakupu akcji i otrzymania największego zysku dla następujących przypuszczeń:

a) są znane prawdopodobieństwa р₁ i р₂ stanów rynku R₁ i R₂ na koniec roku;

b) prawdopodobieństwa р₁ i р₂ stanów rynku R₁ i R₂ na koniec roku są nieznane.

b=14 a₁=6 a₂=4 a₃=4 p₁=0,4 p₂=0,6 γ=0,6 d₁₁=7 d₁₂=14 d₂₁=8 d₂₂=10 d₃₁=12 d₃₂=5.

Rozwiązanie.

1) Jednym z uczestników rozpatrywanej w zadaniu sytuacji jest bank, który kupuje akcji firmy dla osiągnięcia największego zysku. Jeżeli przekształcić zadanie do postaci gry, wtedy bank występuje jako pierwszy gracz i dąży do maksymalizacji zysku od akcji firmy. Drugim uczestnikiem (drugim graczem) będzie rynek, gdzie w ogólnym przypadku losowo zmieniają się ceny na akcji. Rynek można traktować jako „naturę”, która losowo realizuje swoi stany. Drugi gracz jest obojętny do wygranej pierwszego gracza. Podobna sytuacja jest charakterystyczna dla gry statystycznej.

b=14 strategii	a1=6	a2=4	a3=4
1	1	1	1
2	1	2	0
3	1	0	2

Kupując akcji na sumę b, bank może kupić akcji w różnych cenach. Możliwe następujące kombinacji kupowania akcji:

Z tabeli wynika, że u pierwszego gracza istnieje 3 czyste strategii:

1-a: kupić 1 akcją z ceną a₁, 1 - z ceną a₂ i 1- z ceną a₃;

2-a: kupić 1 akcją z ceną a₁, 2 - z ceną a₂;

3-a: kupić 1 akcją z ceną a₁, 2 - z ceną a₃;

U drugiego gracza (natury) możliwe dwie strategii R₁ i R₂.

2) zapiszemy macierz płac. Dla tego obliczymy zysk banku na koniec roku. Macierz płac ma postać:

Strategii gracza 1\ graca 2	R1	R2
1	1*7+1*8+1*12-14=13	1*14+1*10+1*5-14=15
2	1*7+2*8-14=9	1*14+2*10-14=20
3	1*7+2*12-14=17	1*14+2*5-14=10

Otrzymujemy macierz 3 х 2, która jest macierzą płac:

Dla rozwiązania gry obliczymy dolną  i górną  czystą ceną gry. Na podstawie definicji
i
. Ponieważ >, gra nie ma punktu siodłowego i dla tego nie ma rozwiązania w czystych strategiach. Dolną ceną gry jest =10 , górną - =15. To oznacza, że bank otrzyma minimalny zysk =10, jeśli kupi 1 akcje z ceną a₁ i 2 akcje z ceną a₃ i stan rynku będzie R₂. Bank otrzyma maksymalny zysk =15, jeśli kupi 1 akcje z cenami a₁ , a₂ , a₃ i stan rynku będzie R₂.

3) zrobimy rekomendacji dla zakupu akcji i otrzymania największego zysku dla następujących przypuszczeń:

a) są znane prawdopodobieństwa р₁ i р₂ stanów rynku R₁ i R₂ na koniec roku;

Dla tego wykorzystujemy kryterium Beyes'a i obliczymy

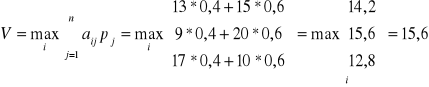
przy i=2, co oznacza, że optymalną będzie strategia A₂: kupić 1 akcją z ceną a₁, 2 - z ceną a₂.

b) prawdopodobieństwa р₁ i р₂ stanów rynku R₁ i R₂ na koniec roku są nieznane.

b.1.) Wykorzystujemy kryterium Laplace'a (prawdopodobieństwa stanów rynka są takie samy i równe 0,5). Obliczamy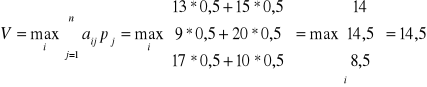
przy i=2, co oznacza, że optymalną będzie strategia A₂: kupić 1 akcją z ceną a₁, 2 - z ceną a₂.

b.2.) Wykorzystujemy kryterium Walda i obliczamy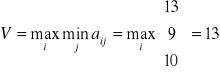
przy i=1, co oznacza, że optymalną będzie strategia A₁: kupić 1 akcją z ceną a₁, 1 - z ceną a₂ i 1- z ceną a₃;

b.3.) Wykorzystujemy kryterium Savage'a i obliczamy

przy i=1. Optymalną będzie strategia A₁.

b.4.) Wykorzystujemy kryterium Hurwicza i obliczamy

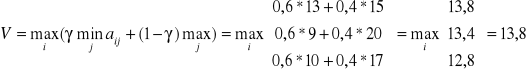
przy i=1. Optymalną będzie strategia A₁.

Możemy zrobić rekomendacji dla banku na wykorzystania pierwszej lub drugiej strategii. Ostateczna decyzja należy do dyrektorów banku.

14

Lekcja 7. Gry dwuosobowe o sumie zero. Czyste i mieszane strategii. Gry statystyczne.

---