Fizyka nr 3 - 29 maja 2010 - Zadania raz jeszcze

Wzory, które będą w zadaniach użyte:

Ruch jednostajny:
Ruch jednostajnie przyspieszony:
,

Ruch po okręgu:
, Prędkość kątowa -
Częstotliwość -

Przyspieszenie dośrodkowe:
Siła dośrodkowa:
Siła grawitacji:

II zasada dynamiki:
Pęd:
Praca:
Moc:

Energia potencjalna:
Energia kinetyczna:

Energia potencjalna układu ciał oddziałujących grawitacyjnie :

Siła sprężystości:
Okres drgań wahadła: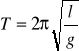

Zadanie 1.

Wzdłuż prostoliniowego odcinka autostrady ustawiono tzw. słupy kilometrowe (odległość pomiędzy dwoma kolejnymi słupami wynosi 1 km). Pozwalają one kierowcy określić, jaką odległość pokonał od wyznaczonego punktu. Poniżej w tabeli zapisano numery kilku kolejnych słupów i odpowiadające im czasy, po upływie których samochód mijał kolejne słupy.

Numer słupa	0	1	2	3	4	5	6
Czas w sekundach	0	50	100	150	200	250	300

1. Ustal na podstawie danych zawartych w tabeli, czy samochód mógł poruszać się
   ruchem jednostajnym. Odpowiedź uzasadnij.

b)Oblicz średnią wartość prędkości samochodu na całym odcinku drogi. Wynik podaj
w m/s.

c)Narysuj wykres zależności drogi od czasu ruchu samochodu. Wykorzystaj dane
zawarte w tabeli.

Zadanie 2.

W tabeli podano wartości przyspieszenia grawitacyjnego na kilku planetach Układu Słonecznego.

Planeta	Merkury	Wenus	Ziemia	Neptun
Wartość przyspieszenia grawitacyjnego (w m/s^2)	3,70	8,87	9,78	11,00

a) Ustal, na której planecie długość wahadła matematycznego o okresie drgań równym
1 s będzie największa. Odpowiedź uzasadnij.

b) Wykaż, że wahadło matematyczne o długości 0,1 m znajdujące się na Merkurym ma
okres drgań równy 1 s.

Zadanie 3.

Bruzdownica jest urządzeniem pozwalającym dokonywać nacięć w ścianach. Zasadniczym jej elementem są dwie tarcze - o promieniu 12,5 cm każda - umieszczone na wspólnej osi. Każda z tarcz podczas pracy wykonuje 8400 obrotów w ciągu jednej minuty.

a) Oblicz okres obrotu tarczy w czasie pracy. Wynik podaj w sekundach

b)Wykaż, że wartość prędkości liniowej punktu leżącego na brzegu wirującej tarczy
wynosi około 110 m/s.

3. Oblicz wartość przyspieszenia dośrodkowego punktu leżącego na brzegu wirującej
   tarczy. Do obliczeń przyjmij, że wartość prędkości liniowej punktu leżącego na brzegu
   tarczy wynosi 110 m/s.

Zadanie 4.

Tomek wchodzi po schodach z parteru na piętro. Różnica wysokości między parterem a piętrem wynosi 3 m, a łączna długość dwóch odcinków schodów jest równa 6 m. Wektor całkowitego przemieszczenia Tomka ma wartość: A. 3 m B. 4,5 m C.6 m D.9 m

Zadanie 5.

Ciężar człowieka o masie 60 kg na pewnej planecie wynosi 600 N. Oblicz wartość przyspieszenia grawitacyjnego na tej planecie.

Zadanie 6.

Na dwóch metalowych kulach, zawieszonych na nieprzewodzących nitkach, umieszczono odpowiednio ładunki elektryczne +2 mC i -5 mC. Po zetknięciu obu kul całkowity ładunek na kulach był równy:

A. +3 mC B. +7 mC C. -3 mC D. -7 mC

Zadanie 7.

Statek wycieczkowy rozwija średnią szybkość v_s =12 km/h. Szybkość prądu rzeki wynosi v_p=18km/h. Z B do C, z prądem rzeki, statek płynie 15 minut.

1. Oblicz odległość między przystaniami.

2. Oblicz, ile czasu będzie płynął statek z C do B.

3. Oblicz średnią szybkość statku na trasie B-C-B, jeżeli w C byt 10 minutowy postój.

Zadanie 8.

Oblicz masę samochodu, który pod wpływem siły F=575 N w ciągu t = 0,5 min, ruszając z miejsca, osiągnął prędkość o wartości v=54 km/h.

Zadanie 9.

W szybkobieżnej windzie umieszczono wagę sprężynową, na której zawieszono ciężarek o masie m = 500 g. Porównaj wskazanie wagi w poruszającej się windzie ze wskazaniem wagi w spoczyn­ku, gdy:

1. winda jedzie ruchem jednostajnym na dół z prędkością o wartości v=3m/s,

2. winda jedzie ruchem jednostajnie przyspieszonym do góry z przyspieszeniem a = 2 m/s²,

Oblicz wartość siły działającej na ciężarek,

Zadanie 10.

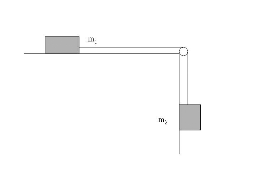
Dwa klocki o masach m₁=500 g i m₂=300 g poruszają się bez tarcia w kierunku masy m₂ tak jak na rysunku. W obliczeniach przyjmij g=10 m/s².

1. Narysuj wszystkie siły działające w układzie, zachowując odpowiednie proporcje.

2. Oblicz przyspieszenie układu ciał.

3. Oblicz siłę naciągu nici.

Zadanie 11.

Na człowieka stojącego na równiku działa odśrodkowa siła bezwładności F=2,5 N. Oblicz jego masę. Przyjmij, że Ziemia obraca się wokół swojej osi z prędkością liniową v= 463 m/s. Promień równika r = 6370 km.

Zadanie 12.

Do podstawowych wielkości układu SI należą:

1. czas, prędkość, siła

2. droga, przyspieszenie, siła

3. droga, czas, masa

4. prędkość, przyspieszenie, siła

Zadanie 13.

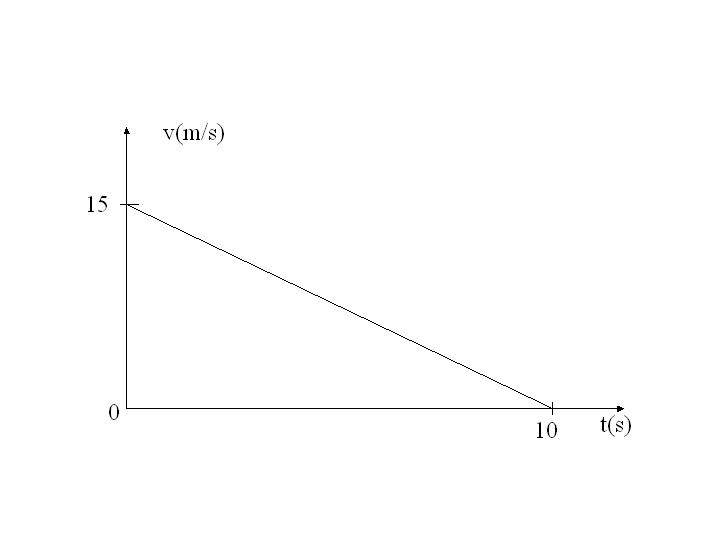
Wykres przedstawia zależność prędkości pewnego ciała od czasu. Droga przebyta przez ciało w ciągu 10 s wynosi:

A) 10m B) 15 m C)75 m D) 150 m

Zadanie 14.

Krążek hokejowy o ciężarze K porusza się po lodzie ze stałą prędkością. Wypadkowa sił działających na krą­żek jest:

1. równa zero b) równa ciężarowi K c) większa niż ciężar K d) mniejsza niż ciężar K

Zadanie 15.

Masa i ciężar:

a) są sobie równe b) mierzą te same wielkości

c) mierzy się je w kg d) są to różne wielkości fizyczne

Zadanie 16.

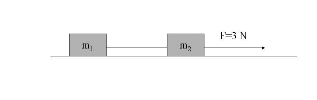
Na dwa ciała przedstawione na rysunku działa sita F. Przyspieszenie większego klocka wyraża wzór:

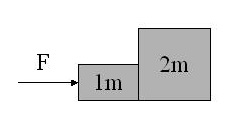
Zadanie 17.

Sanki o masie m₁= 2kg poruszają się w kierunku poziomym z prędkością o wartości v=5 m/s. Ob­licz, jaka dodatkowa masa musiałaby spaść na sanki, aby ich wartość prędkości zmalała o Δv= 1 m/s.

Zadanie 18.

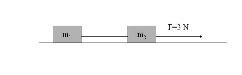
Dwa klocki o masach m₁ i m₂ poruszają się tak jak na rysunku z przyspieszeniem a=5 m/s². Siła naciągu nici ma wartość F=2 N. Narysuj siły naciągu. Oblicz masy ciał. Pomiń tarcie.

Zadanie 19.

W parku zbudowano wypukły mostek o promieniu r = 2,5 m. Oblicz wartość prędkości rowerzysty, przy której znajdowałby się on (w momencie przejazdu przez mostek) przez chwilę w stanie nieważkości. Wykonaj rysunek. Wskaż punkt, w którym będzie to możliwe. W obliczeniach przyjmij g = 10 m/s².

Zadanie 20.

Mars porusza się dookoła Słońca po orbicie o promieniu r = 227,90 mln km. Okres obiegu Marsa dookoła Słońca wynosi T= 1,88 lat. Oblicz częstotliwość obiegu Marsa oraz jego wartość prędkości liniowej w ruchu dookoła Słońca i wyraź ją w kilometrach na sekundę.

Zadanie 21.

„Diabelski Młyn" to koło o średnicy d=12 m. Każdy wagonik zabiera 4 osoby, z których każda ma masę średnio m = 80 kg każda. Oblicz nacisk ludzi siedzących w wagoniku na jego podłoże, gdy znajduje się on w najwyższym punkcie. Wykonaj rysunek. Przyjmij, że wagonik porusza się ruchem jednostajnym po okręgu z prędkością o wartości v=9 km/h. W obliczeniach przyjmij g=10 m/s².

Zadanie 21.

Podstawowe jednostki układu SI to: a)km, kg, K b)N, K, A c)A, V, W d) s, K, A

Zadanie 22.

Kropla deszczu spada dokładnie w kierunku pionowym. Zaobserwowano, że prędkość kropli wzrasta w każdej sekundzie o jednakową wartość. Wypadkowa sił działających na kroplę jest:

1. równa zero b) różna od zera c) stała i różna od zera d) zmienna i różna od zera.

Zadanie 23.

Karol strzela do spoczywającego jabłka o masie m₁= 200 g pociskiem o masie m₂= 5 g wystrze­lonym z prędkością o wartości v = 300 m/s w kierunku poziomym. Oblicz wartość prędkości jabłka, jeżeli pocisk wbił się w nie.

Zadanie 24.

Gdyby Ziemia poruszała się z prędkością o wartości v = 7981 m/s człowiek stojący na równiku odczuwałby stan nieważkości. Wykaż na tej podstawie, że promień Ziemi wynosi R = 6370km.

Zadanie 25.

Prędkość liniowa Jowisza w ruchu dookoła Słońca po orbicie o promieniu r = 778,30 mln km ma wartość v= 13 m/s. Oblicz okres obiegu Jowisza dookoła Słońca i wyraź go w latach. Oblicz przyspie­szenie dośrodkowe Jowisza. W ob­liczeniach przyjmij g = g= 10 m/s².

Zadanie 26.

Rowerzysta porusza się z prędkością o wartości v = 36 m/s po okręgu o promieniu r = 60 m. Ob­licz, pod jakim kątem musi się on nachylić do poziomu, aby nie wypaść z łuku. Wykonaj rysunek. W obliczeniach przyjmij g= 10 m/s².

Zadanie 27.

Schody ruchome ustawione są pod kątem a = 45° do poziomu i przenoszą ludzi na poziom znaj­dujący się o h - 6,5 m wyżej. Na schodach może znajdować się maksymalnie 20 osób. Oblicz długość schodów. Oblicz energię potencjalną, jaką zyska człowiek o masie m = 60 kg, wjeżdżając na wyższy poziom.

Zadanie 28.

Samochód porusza się po poziomej drodze ze stałą szybkością v. Siły oporu powietrza i tarcie wynoszą łącznie F. Odpowiedz, ile wynosi sita ciągu samochodu. Odpowiedź uzasadnij. Wykaż, że moc samochodu poruszającego się ruchem jednostajnym wyraża się wzorem P = Fv.

Zadanie 29.

Cząsteczki tlenu poruszają się ze średnią szybkością v=490 m/s. Oblicz pęd i energię kinetyczną molekuły, jeśli masa cząsteczki tlenu m = 5,31 • 10 ²⁶ kg.

Zadanie 30.

Samochód o masie m = 1t porusza się ruchem jednostajnym po torze poziomym. Pęd samocho­du wynosi p= 15000 kgm/s

a)Oblicz jego szybkość i wyraź ją w kilometrach na godzinę.

2. Oblicz energię kinetyczną samochodu.

3. Oblicz drogę hamowania, jeśli średnia sita hamująca F= 2,5 kN.

Zadanie 31.

Winda osobowa przeznaczona jest do przewozu 20 osób o masie 80 kg każda.

a) Oblicz udźwig windy.

b) Oblicz minimalną pracę, jaką muszą wykonać silniki windy, jeżeli w ciągu t = 50 s przemieszcza się ona bez zatrzymywania na wysokość h = 6 m.

Zadanie 32.

Silnik samochodu osobowego o masie m rozwija moc P. Prędkość v samochodu można obliczyć ze wzoru:

Zadanie 33.

Jeśli na klocek działa stała niezrównoważona sita w kierunku ruchu klocka, wówczas jego ener­gia kinetyczna:

1. rośnie b) maleje c) nie zmienia się d) wynosi zero.

Zadanie 34.

Dwa ciała o masach m₁= 0,5 kg i m₂= 2 kg poruszają się odpowiednio z prędkością v₁ i v₂. Energie kinetyczne tych ciał są równe. Prędkość v₁ w stosunku do v₂ jest:

1. 4 razy mniejsza b) 4 razy większa c) 2 razy większa d) 2 razy mniejsza.

Zadanie 34.

Kulkę wystrzelono pionowo do góry. Podczas wznoszenia jej energia potencjalna:

1. rośnie proporcjonalnie do czasu

2. maleje proporcjonalnie do czasu

3. rośnie proporcjonalnie do wysokości

4. maleje proporcjonalnie do wysokości

Zadanie 35.

Jednostką mocy w układzie SI jest: a) wat b) dżul c) paskal d) koń mechaniczny

Zadanie 36.

Silnik, którego moc wynosi P=15kW, w czasie t=10 minut wykonał pracę:
a) 25 J b) 150 J c) 150 kJ d) 9 MJ

Zadanie 37.

Wyprowadź wyrażenie na I i II prędkość kosmiczną dla Ziemi i wylicz jej wartość liczbową.

Zadanie 38.

Siła grawitacji działająca między dwoma ciałami jest odwrotnie proporcjonalna do:

1. masy ciała

2. iloczynu mas tych ciał

3. odległości między ich środkami

4. kwadratu odległości między ich środkami

1

---