1
Rachunek różniczkowy funkcji wielu zmiennych
1.1 Definicja i interpretacja geometryczna funkcji rzeczywistej o dwóch zmiennych rzeczywistych.
Jeżeli ![]()
pryporządkowana jest dokładnie jedna wart. Z∈R to mówimy, że w zb Z określona jest f. rzeczywista o dwuch zmiennych x,y i ozn. ją Z=f(x,y) lub f:D→R.
Def. Granica podwójna w pkt.
Liczbę g nazywamy granicą funkcji f(x,y) w Po gdy dla każdego ciągu punktów Pn (Pn ? Po, Pn ? Po, Pn ∈ D) f(Pn) ? g
![]()
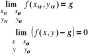
![]()
1.2. Def. funkcji ciągłej w punkcie.
Niech Po(xo,yo) należy do obszaru określoności funkcji f(x,y).
Def. f(x,y) nazywamy ciągłą w punkcie Po jeżeli:
1o f posiada granicę w Po
2o f posiada wartość w Po
3o g=f(xo,yo)=f(Po)
![]()
1.3. Def. pochodnej cząstkowej I rzędu ze względu na zmienną x dla funkcji o dwóch zmiennych.
Niech f(x,y) określona w Q(Po) 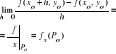
Tw. Schwarza.
Jeżeli f(x,y) ma w obszarze D ciągłe pochodne mieszane II rzędu, to ![]()
dla każdego punktu tego obszaru.
1.4. Def. pochodnej cząstkowej I rzędu ze względu na zmienną y.
Niech f(x,y) określona w Q(Po) 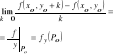
Def. pochodnej kierunkowej dla funkcji o dwóch zmiennych.
f : Q(Po)
![]()
P∈Q(Po); P≠Po ![]()
jeżeli istnieje ta granica, to będziemy ją nazywać pochodną kierunkową w kierunku prostej Pos.
1.5. Wzory: poch. funkcji uwikłanej ![]()
.
1.6. Wzory: pochodna funkcji złożonej o jednej i dwóch zmiennych.
1) jednej zmiennej:
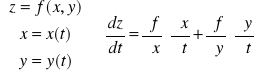
2) dwóch zmiennych:
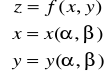
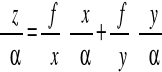
![]()
1.7. Def. różniczki zupełnej I rzędu
Niech f(x,y) będzie różniczkowalna w punkcie Q(Po). Składnik liniowy ![]()
nazywamy różniczką zupełną funkcji f(x,y) w punkcie Po oznaczamy symbolem ![]()
1.8. Warunek konieczny istnienia ekstremum.
Jeżeli f(x,y) ma w Po poch. ![]()
, ![]()
i ma w tym punkcie ekstremum, to ![]()
; ![]()
.
Warunek wystarczający.
Jeżeli ![]()
i ![]()
, to f(x,y) posiada w Po ekstremum gdy W(Po )>0 (![]()
, ![]()
). 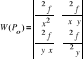
.
1.9)warunek konieczny i wystarczający istnienia ekstremum funkcji dwóch zmiennych.
Warunek konieczny:
Jeżeli funkcja f(x,y) ma pochodne cząstkowe pierwszego rzędu w punkcie P0(x0,y0) i ma w tym punkcie ekstremum to: fx(p0) =0 ; fy(p0)=0. Punkt P(x0,y0),w którym spełniony jest ten waruneknazywa się punktem stacjonarnym funkcji f(x,y). Jeżeli więc funkcja f(x,y) ma w pewnym obszarze pochodne cząstkowe rzędu pierwszego , to może mieć ona ekstremum jedynie w tych punktach tego obszaru, które są jej punktami stacjonarnymi.
Warunek wystarczający ekstremum:
Jeżeli f-cja f(x,y) jest klasy c2 w pewnym otoczeniu punktu P(x0,y0), a ponadto:
1) fx (P0) = 0 i fy (P0) = 0
2)
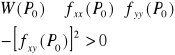
1.10. Def.i przykład całki zależnej od parametru.
Niech K (x,y) będzie f-cją dwóch zmiennych, określoną dla x∈<a,b> i y∈Y, gdzie Y jest pewnym przedziałem. Jeżeli dla każdego y∈Y istnieje całka oznaczona 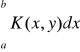
to w przedziale Y jest określona f-cja F(y)
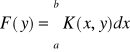
Zmienną y, występującą we wzorze: 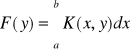
nazywamy parametrem całkowania, o całce zaś mówimy, że jest zależna od parametru.
1.11. Tw. o całce zależnej od parametru.
Jeżeli f-cja K(x,y) jest ciągła w prostokącie P: a ≤ x ≤b , α ≤ y ≤ β, to f-cja 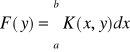
Jest ciągła w przedziale <α,β>. Jeżeli ponadto istnieje w prostokącie P ciągła
pochodna cząstkowa
![]()
to w przedziale <α,β> istnieje pochodna F'(y) przy czym:
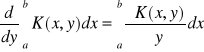
3
Równanie różniczkowe zwyczajne
3.1. Def. równania różniczkowego liniowego.
Równanie różniczkowe postaci ![]()
, liniowe względem y i y', nazywamy równaniem liniowym rzędu I.
3.2. Def. równania różniczkowego Bernoulliego.
Równanie postaci ![]()
nazywamy równaniem różniczkowym Bernoulliego, gdzie p(x) i q(x) są funkcjami ciągłymi w pewnym wspólnyym przedziale a<x<b, a n jest dowolną liczbą rzeczywistą.
Dla n=0 otrzymujemy równanie różniczkowe liniowe.
Dla n=1 otrzymujemy równanie różniczkowe liniowe jednorodne względem y i y', a więc równanie, w którym zmienne dadzą się rozdzielić.
3.3. Def. równania różniczkowego zupełnego.
Równaniem różniczkowym zupełnym nazywamy równanie różniczkowe rzędu I postaci ![]()
, w którym funkcje P(x,y) i Q(x,y) są ciągłe w pewnym obszarze D i takie, że wyrażenie ![]()
jest różniczką zupełną pewnej funkcji dwóch zmiennych F(x,y) określonej w obszarze D. Oznacza to, że w obszarze D istnieje taka różniczkowalna funkcja F(x,y), że zachodzą związki: ![]()
, ![]()
w każdym punkcie tego obszaru.
3.4.Twierdzenie I o czynniku całkującym dla równania różniczkowego zupełnego
Jeżeli
![]()
to μ(x,y)=![]()
μ(x,y)-czynnik całkujący
![]()
3.5.Twierdzenie II o czynniku całkującym dla równania różniczkowego zupełnego
Jeżeli
![]()
to μ(x,y)=![]()
μ(x,y)-czynnik całkujący
3.6.Równanie różniczkowe Clairauta.
Równanie postaci ![]()
![]()
gdzie 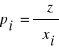
(i=1,2,...,n); jest to tzw. równanie Clairauta. Całką zupełną takiego równania jest ![]()
![]()
gdzie a1,a2,...,an są dowolnymi parametrami.
3.7.Równ. różniczkowe Lagrange'a.
Równanie postaci ![]()
nazywamy równaniem Langrange'a. Może ono być scałkowane w kwadraturach. Jeżeli a(p)+b(p)p=0 przy p=p0, to a(p0)x+b(p0)y+c(p0)=0 jest całką osobliwą równania Lagrange'a.
3.8. Def. równania różniczkowego liniowego II rzędu o stałych współczynnikach.
Równanie różniczkowe liniowe rzędu II o stałych współczynnikach ma postać: ![]()
(a≠0)
Równanie to jest liniowe względem y i jej poch., natomiast funkcja f zmiennej x może być w dowolnej postaci, a litery a, b, c oznaczają dowolne stałe.
3.11. Def. równania różniczkowego liniowego rzędu n o stałych współczynnikach.
Równaniem różniczkowym liniowym rzędu n o współczynnikach stałych nazywamy równanie postaci: ![]()
; ![]()
.
Równanie to, będące bezpośrednim uogólnieniem równania rzędu II, jest liniowe względem y i wszystkich jej pochodnych; występujące w równaniu współczynniki ao, a1,…,an są stałe, a f(x) jest dowolną funkcją.
3.12. Zagadnienie trajektorii.
Trajektorią izogonalną rodziny krzywych nazywamy krzywą, która w każdym swym punkcie przecina krzywą rodziny przechodzącą przez ten punkt pod stałym kątem ![]()
. Jeżeli ![]()
to trajektorię nazywamy ortogonalną.
Tw. Jeżeli rodzina krzywych F(x,y,c)=0 ma równanie postaci f(x,y,y')=0 to rodzina trajektorii ortogonalnych ma równanie ![]()
, a rodzina trajektorii izogonalnych: ![]()
.
4
Przekształcenie Laplace'a
4.1. Definicja przekształcenia Laplace'a.
Ko - klasa oryginału
K - zb. wszystkich F o zmiennej s
α: Ko→K
![]()
![]()
s∈α
4.2. Własności podstawowe przekształcenia Laplace'a
1)£[0]=0
2) £[η(x)]=![]()
Re(s)>0
3)n![]()
No![]()
4.3. Wzór: różniczkowanie oryginału (dla pochodnej ni rzędu). Dowolna własność przekształcenia Laplace'a.
![]()
4.4. Wzór: całkowanie oryginału. Dowolna własność przekształcenia Laplace'a.
![]()
4.5. Twierdzenie o podobieństwie dla przekształcenia Laplace'a.
Jeżeli f(t)∈Ko oraz a>0 to ![]()
4.6. Twierdzenie o przesunięciu dla przekształcenia Laplace'a.
Jeżeli f(t) )∈Ko oraz to≥0, to ![]()
4.7. Twierdzenie o tłumieniu dla przekształcenia Laplace'a.
Jeżeli f(x)∈Ko dla dowolnego stałego a ![]()
![]()
4.8. Definicja splotu funkcji.
Niech![]()
f,g∈L (<0,x>), to ![]()
- nazywamy splotem funkcji w przedziale <0,x>
4.9. Własności splotu funkcji.
1)![]()
2) ![]()
4.10. Twierdzenie Borela.
Jeżeli f1(t) i f2(t) są oryginałami, to istnieje α-transformata ich splotu, przy czym ![]()
5
Szeregi liczbowe
5.1. Definicja i zbieżność szeregu geometrycznego.
Ciąg nieskończony (Sn) o wyrazach: S1=a1, S2=a1+a1q, S3=a1+a1q+a1q2, Sn=a1+a1q+...+a1qn-1nazywamy ciągiem sum częściowych ciągu geometrycznego (Sn) lub szeregiem geometrycznym, co piszemy:
a1+a1q+...+a1qn-1+...=![]()
Ciąg sum częściowych (Sn) ciągu geometrycznego jest zbieżny i ma granicę S(szereg geometryczny ma sumę S) wtedy i tylko wtedy , gdy |q|<1 lub a1=0, wówczas:
![]()
, gdy |q| < 1, lub S=0, gdy a1= 0.
5.2. Definicja i zbieżność szeregu harmonicznego.
Szereg który spełnia warunek szeregu:
lim an=0, jednakże jest rozbieżny, jest tzw. szeregiem harmonicznym:
![]()
, czyli szereg ![]()
szereg ten nazywa się harmoniczny, dlatego, że każdy jego wyraz (oprócz pierwszego) jest średnią harmoniczną wyrazu poprzedniego i następnego, tzn. ,że odwrotność n-tego wyrazu (n ≥2) jest równa połowie sumy odwrotności wyrazów:
(n-1)-go i (a+1)-go.
5.3Warunek konieczny zbieżności szeregu liczbowego.
![]()
![]()
![]()
![]()
![]()
![]()
Warunkiem koniecznym zbieżności szeregu liczb jest, aby jego ogólny wyraz dążył do 0.
5.4 5.5 Kryterium d'Alamberta zbieżności, rozbieżności szeregu liczbowego.
Jeżeli ![]()
oraz 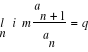
to ![]()
jest zbieżny gdy q<1, rozbieżny gdy q>1. Przy q=1 kryterium nie daje rozstrzygnięcia: szereg może być zbieżny albo rozbieżny.
5.6 5.7 Kryterium Cauchy'ego zbieżności i rozbieżności szeregu liczbowego.
Jeżeli ![]()
oraz ![]()
to szereg ![]()
jest zbieżny gdy q<1, a rozbieżny gdy q>1; gdy q=1 to kryterium nie daje rozstrzygnięcia.
5.8 Kryterium porównawcze zbieżności szeregu liczbowego.
Jeżeli dla szeregu ![]()
, gdzie ![]()
można wskazać taki zbieżny szereg ![]()
, dla którego zachodzi ![]()
to szereg ![]()
jest też szeregiem zbieżnym.
5.9 Kryterium porównawcze rozbieżności szeregu liczbowego.
Jeżeli dla szeregu ![]()
można wskazać taki rozbieżny szereg ![]()
, w którym ![]()
to szereg ![]()
jest również szeregiem rozbieżnym.
5.10 Kryterium całkowe zbieżności szeregu liczbowego.
Szereg o wyrazie ogólnym ![]()
jest rozbieżny, jeżeli f(x) jest funkcją monotonicznie malejącą i całka niewłaściwa ![]()
jest zbieżna; natomiast jeżeli całka ta jest rozbieżna to szereg o wyrazie ogólnym f(n) jest rozbieżny. Przy czym dolną granicę całkowania c należy tak obrać, żeby funkcja f(x) w przedziale c < x < ∞ była oznaczona i nie miała punktów nieciągłości.
5.11 Definicja szeregu liczbowego przemiennego.
Szereg ![]()
![]()
gdzie ![]()
są liczbami dodatnimi, nazywamy szeregiem przemiennym.
5.12 Kryterium Leibniza zbieżności szeregu przemiennego.
Jeżeli: ![]()
oraz ![]()
to szereg przemienny jest szeregiem zbieżnym.
5.13. Definicja szeregu zbieżnego bezwzględnie.
Szereg zbieżny ![]()
nazywamy bezwzględnie zbieżnym jeżeli jest zbieżny szereg
![]()
Szereg zbieżny ![]()
nazywamy warunkowo zbieżnym jeżeli szereg
![]()
jest rozbieżny
5.12. Tw. o związku pomiędzy zbieżnością zwyczajną i bezwzględną.
Jeżeli szereg ![]()
jest zbieżny, to jest zbieżny bezwzględnie szereg ![]()
6
Szeregi funkcyjne
6.1 Definicja szeregu potęgowego.
Szeregiem potęgowym nazywamy szereg funkcyjny postaci ![]()
![]()
lub postaci ![]()
![]()
, gdzie ![]()
(i=1,2...) są stałymi współczynnikami.
6.2 Wzory na promień zbieżności szeregu potęgowego.
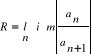
Promieniem zbieżności szeregu potęgowego nazywamy kres górny zbioru wart bezwzg. wszystkich wartości x, dla których ten szereg jest zbieżny (oznaczamy jako R).
6.3, 6.4, 6.5, Znaczenie promienia zbieżności szeregu potęgowego dla R=r > 0, R=0, R=∞.
Jeżeli istnieje granica 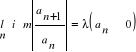
![]()
to 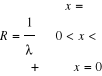
6.6 Twierdzenie o rozwinięciu funkcji w szereg Taylora.
Każda funkcja ![]()
, analityczna wewnatrz pewnego koła o środku a, może być w każdym punkcie tego koła w sposób jednoznaczny przedstawiona w postaci szeregu potęgowego: ![]()
, gdzie współczynnikami ![]()
rozwinięcia są liczby zespolone określone wzorem ![]()
. W ten sposób otrzymujemy szereg Taylora: ![]()
![]()
![]()
6.7 Twierdzenie o rozwinięciu funkcji w szereg Maclaurina.
Jest to rozwinięcie funkcji ![]()
w szereg według potęg zmiennej x. Jest to przypadek szczególny szeregu Taylora dla a=0. ![]()
![]()
![]()
Reszta szeregu Maclaurina: ![]()
gdzie ![]()
oraz ![]()
6.8 Warunki Dirichleta.
Mówimy, że funkcja f(x) spełnia w przedziale domkniętym warunki Dirichleta jeżeli:
-f(x)przedziałami monotoniczna w (a,b)
-f(x) ciągła w (a,b) z wyjątkiem skończonej liczby punktów nieciągłości pierwszego rodzaju, przy czym w każdym punkcie nieciągłości: ![]()
![]()
6.9.Definicja szeregu Fouriera w przedziale(-π,π).
Jeżeli f-cja f spełnia warunek Dirichleta w przedziale <-π,π> to:
![]()
, gdzie 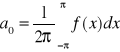
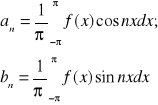
7
Całka podwójna
7.1. Tw. o zmianie całki podwójnej na iterowaną dla obszaru normalnego względem osi OX.
Jeżeli obszar D jest obszarem normalnym względem osi OX danym nierównościami ![]()
, ![]()
, przy czym ![]()
, gdy ![]()
, to ![]()
. Występujące funkcje są ciągłe i ograniczone w D.
7.2. Tw. o zmianie całki podwójnej na iterowaną dla obszaru normalnego względem osi OY.
Jeżeli obszar D jest obszarem normalnym względem osi OY danym nierównościami ![]()
, ![]()
, przy czym ![]()
, gdy ![]()
, to ![]()
.
Występujące funkcje są ciągłe i ograniczone w D.
7.3. Tw. o zmianie zmiennych w całce podwójnej.
Jeżeli: 1o odwzorowanie ![]()
; ![]()
przekształca jednoznacznie wnętrze obszaru Δ (regularnego) na wnętrze obszaru D (regularnego),
2o ![]()
,
3o ![]()
![]()
- domknięty i ograniczony,
4o ![]()
w ![]()
,to ![]()
7.4. Tw. o zmianie zmiennych prostokątnych na biegunowe w całce podwójnej.
Wprowadzamy współrzędne biegunowe ![]()
, ![]()
i mamy ![]()
7.5. Zastosowanie całki podwójnej: objętość bryły.
1o ![]()
![]()
2o ![]()
, ![]()
![]()
.
7.6. Zastosowanie całki podwójnej: pole płata powierzchniowego.
D - obszar płaski, regularny, ograniczony jedną krzywą zamkniętą K,
Niech ![]()
![]()
.
7.7. Zastosowanie całki podwójnej: masa obszaru płaskiego.
Jeżeli ![]()
![]()
- gęstość obszaru ![]()
(domknięty i ograniczony), to ![]()
.
7.8. Zastosowanie całki podwójnej: moment statyczny i moment bezwładności obszaru płaskiego.
![]()
- gęstość powierzchniowa masy
![]()
- masa
Moment statyczny:
![]()
.
Moment bezwładności:
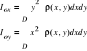
.
7.9. Zastosowanie całki podwójnej: środek ciężkości obszaru płaskiego.
![]()
.
8
Całki potrójne
8.1 Tw. o zamianie całki potrójnej na podwójną dla bryły normalnej względem płaszczyzny XOY.
Jeżeli:
1. V - bryła normalna względem płaszczyzny XOY
2. π1: z = ϕ1(x,y), (x,y) ∈Ω
3. π2: z = ϕ2(x,y), (x,y) ∈Ω, to:
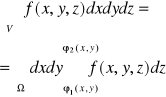
8.2 Twierdzenie o zamianie zmiennych w całce potrójnej.
Jeżeli:
1. odwzorowanie x=x(u,v,w); y=y(u,y,w), z=z(u,v,w), odwzorowuje wzajemnie jednoznacznie wnętrze U obszaru regularnego ![]()
na wnętrze Ω obszaru regularnego ![]()
2. każda z funkcji (x,y,z) jest klasy C1 w pewnym obszarze zawierającym ![]()
w swym wnętrzu
3. f(x,y,z) jest funkcja ciągłą w ![]()
oraz jakobian przekształcenia:
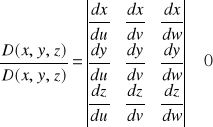
w obszarze U, to:
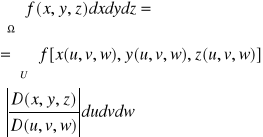
8.3 Twierdzenie o zamianie zmiennych prostokątnych na zmienne sferyczne w całce potrójnej
Jeżeli:
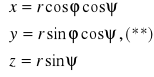
to:
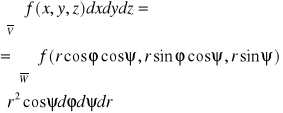
założenie:
1. Odwzorowanie (**) odwzoruje jednokładnie wnętrze W obszaru regularnego W na wnętrze V obszaru regularnego ![]()
.
2. Każda z funkcji (x,y,z) jest klasy C1 w pewnym obszarze zawierającym W w samym wnętrzu.
3. f(x,y,z) jest ciągła w V.
8.4 Zastosowanie całki potrójnej: objętość bryły.
Jeżeli ![]()
jest bryłą normalną to :
![]()
8.5 Zastosowanie całki potrójnej: masa bryły.
Jeżeli: ρ (x,y,z) jest gęstością objętościową masy prostopadłościanu P, to całka potrójna
![]()
przedstawia masę tego prostopadłościanu.
9
Całka krzywoliniowa nieskierowana
9.3. Tw. o zamianie całki krzywoliniowej nieskierowanej na pojedyńczą dla krzywej płaskiej o równaniach parametrycznych.
Jeżeli funkcja ![]()
jest ciągła na otwartym, zwykłym łuku gładkim L o przedstawieniu parametrycznym ![]()
, ![]()
, ![]()
, to całka ![]()
istnieje, przy czym ![]()
9.5. Zastosowanie całki krzywoliniowej nieskierowanej: długość krzywej.
Jeżeli ![]()
, to ciąg ![]()
jest stały ![]()
, więc całka ![]()
przedstawia długość łuku ![]()
.
9.6. Zastosowanie całki krzywoliniowej nieskierowanej: masa krzywej.
Jeżeli ![]()
jest gęstością liniową masy łuku L, to całka ![]()
przedstawia masę tego łuku.
10
Całka krzywoliniowa skierowana
10.3. Tw. o zamianie całki krzywoliniowej skierowanej na pojedyńczą dla krzywej płaskiej o równaniach parametrycznych.
Jeżeli ![]()
, ![]()
są ciągłe na otwartym zwykłym, gładkim łuku ![]()
o przedstawieniu ![]()
, ![]()
, ![]()
zgodnym z kierunkiem tego łuku, to całka ![]()
istnieje, przy czym 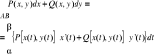
10.5. Napisać wzór na pole obszaru płaskiego przy pomocy całki krzywoliniowej skierowanej.
Jeżeli P i Q ![]()
normalnego względem osi OX i OY jednocześnie, którego brzeg K jest zorientowany dodatnio względem wnętrza, to całka podwójna po obszarze ![]()
![]()
.10.6. Zastosowanie całki krzywoliniowej skierowanej: praca siły.
W-praca siły ![]()
na drodze AB
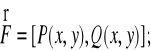
to:
![]()
Praca siły potencjalnego pola równa jest różnicy potencjału na końcach krzywych
.
10.7. Sformułować i udowodnić twierdzenie o niezależności całki krzywoliniowej skierowanej od drogi całkowania.
Tw. Jeżeli funkcje P(x,y) i Q(x,y) są klasy C1 w obszarze jednospójnym D, to spełnione równości ![]()
w każdym punkcie tego obszaru jest warunkiem koniecznym i wystarczającym na to, żeby całka ![]()
po otwartym, kawałkami gładkim łuku zwykłym ![]()
nie zależała od kształtu tego łuku, a tylko od punktów AB.
10.8. Sformułować i udowodnić twierdzenie Greena.
Jeżeli ![]()
, ![]()
![]()
![]()
(D domknięty i ograniczony) ,D - obszar normalny względem osi OX i OY, przy czym krzywa K - brzeg obszaru D skierowana dodatnio względem wnętrza, to całka krzywoliniowa po krzywej K (zamkniętej) ![]()
względem wnętrza, to całka podwójna po obszarze Ω
![]()
12
Teoria pola
12.1. Definicja operatora Hamiltona
Operatorem Hamiltona nazywamy wyrażenie postaci
![]()
Operator Nabla
![]()
12.2. Własności operatora Hamiltona
12.3. Definicja gradiendu pola skalarnego
u = (x,y), u∈C1(Ω)
grad 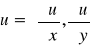
, grad u=∇u
u=u(x,y,z) to:
grad 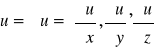
Gdy w obszarze V istnieje funkcja ve c![]()
(V) takie, że składowe pola wektorowego [P,Q,R]wyrażają się wzorem ![]()
,![]()
,![]()
to mówimy, że pole wektorowe jest gradientem funkcji ve, a a funkcję ve nazywamy potencjałem pola.
Możemy zapisać
grad f=![]()
12.4 Własności gradiendu pola skalarnego
grad (cu)=cgradu
grad(u+v)=gradu+gradv
grad(f*g)=ggradf +fgradg
gradf2 =2fgradf
12.5. Definicja dywergencji pola wektorowego
Dywergencją różniczkowalną pola wektorowego ![]()
(M)=[a![]()
,a![]()
a![]()
] oznaczaną div ![]()
nazywamy pole skalarne określone równością
div![]()
![]()
![]()
![]()
Dywergencja w odróżnieniu od gradiendu jest liczbą
12.6. Własności dywergencji pola wektorowego
div
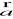
=
*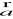
div (c
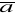
)= c div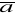
div (
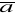
+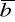
)=div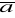
+ div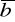
12.7. Definicja rotacji pola wektorowego
Rotacją różniczkowanego pola wektorowego ![]()
(M)=[a![]()
,a![]()
a![]()
] oznaczaną rot ![]()
nazywamy wektor oznaczony przez składowe
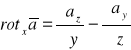
![]()
![]()
12.8. Własności rotacji p.wektorowego
rot (c![]()
) = c rot ![]()
rot (![]()
)= rot![]()
+ rot ![]()
13
Równanie różniczkowe cząstkowe
13.1. Definicja równania różniczkowego cząstkowego II rzędu
F(x,y,y![]()
,…,y![]()
)=0 -równanie różniczkowe zwyczajne n-rzędu
1)![]()
![]()
a![]()
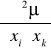
+![]()
b![]()
![]()
+cu=f μ
a![]()
,b![]()
,c,f- funkcje ciągłe zmiennych x![]()
,x![]()
...x![]()
określonych w pewnym obszarze n-wymiarowym, μ -funkcja szukana tych zmiennych, przy czym a![]()
=a![]()
. Gdy f=0, wówczas równanie 1) jest jednorodne
13.2.Klasyfikacja równań różniczkowych cząstkowych II rzędu
1) Formę kwadratową zmiennych x![]()
,...,x![]()
![]()
a![]()
x![]()
x![]()
a![]()
-współczynnik lewej strony równania
![]()
![]()
a![]()
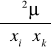
=
![]()
obliczany w dowolnym punkcie obszaru D
2) Forma kanoniczna
![]()
![]()
+![]()
![]()
+...+![]()
![]()
, ![]()
-ma wartość 1,-1lub0
3)Postać kanoniczna
![]()
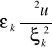
=![]()
(![]()
Mówimy, że równanie jest w punkcie P0 (x![]()
;x![]()
;...;x![]()
)∈D typu:
-hiperbolicznego, gdy wszystkie współczynniki λ1 są różne od zera i wszystkie z wyjątkiem jednego mają ten sam znak
-parabolicznego, gdy wszystkie współczynniki λ1 z wyjątkiem jednego λk są różne od zera i mają ten sam znak oraz współczynnik przy ![]()
jest różny od zera
-eliptycznego, gdy wszystkie współczynniki λ1 są różne od zera i mają ten sam znak
![]()
![]()
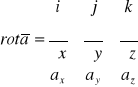
Wyszukiwarka
Podobne podstrony:
matematyka podstawowe wzory i Nieznany
matma Matematyka podstawowe wzory
Matematyka Podstawowe wzory i przykłady
Statystyka - podstawowe wzory 2, Budownictwo Studia, Rok 2, Statystyka Matematyczna
Matematyka, podstawowe wzory 3
Matematyka podstawowe wzory 4 id 282961
Podstawowe wzory na całki, Studia, Zarządzanie, Matematyka w ekonomii i zarządzaniu
Matematyka podstawowe wzory 3
Matematyka podstawowe wzory
matematyka podstawowe wzory i Nieznany
więcej podobnych podstron