Rzeszów, 2005r.

POLITECHNIKA RZESZOWSKA

Im. Ignacego Łukasiewicza

ZAKŁAD PODSTAW ELEKTROTECHNIKI I INFORMATYKI

Projekt z obwodów elektrycznych

Wykonali: Bartłomiej Haraszczuk

Marcin Młynarski

Opiekun: dr inż. Grzegorz Masłowski

1.Temat projektu.

Zaprojektowanie cyfrowego, dolnoprzepustowego filtru Butterwortha dla określonych parametrów, a także analiza zaprojektowanego układu z wykorzystaniem Scilaba.

2.Cel projektu.

Głównym celem projektu jest zapoznanie się z algorytmami projektowania filtrów dolnoprzepustowych Butterwortha. Parametry projektowanego filtru to: częstotliwości graniczne - f_pass1 = 1200 Hz i f_stop1 = 1550 Hz, częstotliwość próbkowania - f_pr = 4000 Hz, tłumienie w paśmie przepustowym A_pass = 3 dB, tłumienie w paśmie zaporowym A_stop = 40 dB.

3.Wstęp teoretyczny.

3.1. Charakterystyka maksymalnie plaska Butterwortha.

Filtr Butterwortha w stosunku do innych filtrów ma najbardziej płaski przebieg charakterystyki amplitudowej w paśmie przepustowym. Odbywa się to kosztem załamania charakterystyki pod koniec pasma przepustowego. Ma on również kiepska charakterystykę fazowa.

W filtrze Butterwortha najważniejszym celem jest uzyskanie maksymalnej płaskości charakterystyki amplitudowej. Charakterystyka powinna zaczynać się maksymalnie płasko dla zerowej częstotliwości i przeginać się dopiero w pobliżu częstotliwości granicznej f_g (f_g jest zwykle częstotliwością 3dB).

Warunki maksymalnej płaskości charakterystyki amplitudowej.

Załóżmy, ze:

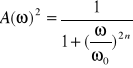
(1)

Można łatwo sprawdzić, ze funkcja spełnia warunek:

dla ω=0 k=0,1,.....n-1 (2)

a wiec warunek maksymalnej płaskości w punkcie ω=0 (przy zadanym n). Stad charakterystykę amplitudowa A(ω) określona wzorem (1) nazywamy charakterystyka maksymalnie płaską rzędu n lub charakterystyka Butterwortha rzędu n. Wykresy maksymalnie płaskiej charakterystyki A(ω) dla różnych n są przedstawione na poniższym rysunku. Charakterystyki A(ω) z rysunku są monotoniczne i dla wartości ω / ω ₀=1 przybierają wartości:

dla ω/ω₀=1 (3)

a wiec maleją w porównaniu z wartością początkową A(0) o 3dB. Ponadto można bez trudu sprawdzić, ze:

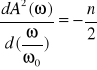
dla ω/ ω₀=1 (4)

a wiec nachylenie charakterystyki A(ω) dla pulsacji 3-decybelowej ω₀, która możemy uznać za pulsacje graniczna miedzy pasmem przepustowym a pasmem zaporowym, jest (co do modułu) niewiele i liniowo rośnie ze wzrostem n. Na poniższym rysunku przedstawiono charakterystyki amplitudowe dla kolejnych n. Rząd określony jest przez liczbę przy K(Ω).

3.2. Transmitancja filtru Butterwortha

Transmitancje H(s) odpowiadająca charakterystyce amplitudowej (1), a wiec transmitancje odpowiedniego filtru Butterwortha aproksymującego idealny filtr dolnoprzepustowy, przedstawiamy następująco:

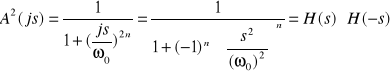
(5)

3.3. Bieguny filtru Butterwortha

Bieguny wyrażenia są położone symetrycznie względem początku układu współrzędnych, tj. jeśli s _k jest biegunem, to również biegunem jest -s _k. Umożliwia to rozdział funkcji (5) na H(s) i H(-s) według położenia biegunów. Wyrażenie (5) możemy przepisać w postaci:

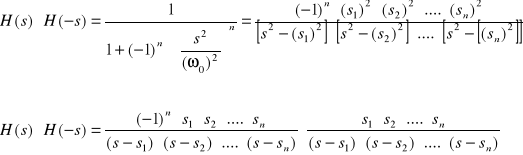
(6)

gdzie przez s₁, s₂,...,s _n oznaczyliśmy bieguny (pierwiastki mianownika) leżące w lewej półpłaszczyźnie Res<0. Na podstawie tego wyrażenia identyfikujemy transmitancje H(s) jako:

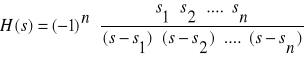
(7)

Pozostaje wyznaczyć wartości s ₁, s₂,...,s _n. Wartości te sa pierwiastkami równania:

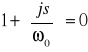
(8)

z którego otrzymujemy:

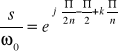
dla k=0,1,….2n-1 (9)

lub:

dla k=0,1,….,n-1 (10)

przy czym pierwiastki w lewej półpłaszczyźnie są określone zależnością:

dla k=0,1,….,n-1 (11)

(6)

Pierwiastki (11) równania (8) leża na okręgu o promieniu ω₀ w odstępach kątowych równych π/n. Wyznaczając kolejno wartości tych pierwiastków, otrzymujemy, zgodnie ze wzorem (7):

n=1 s₁=-ω₀

n=2

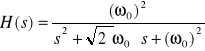
n=3



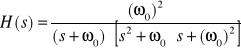
(12)

i tak dalej.

3.4. Wielomian Butterwortha stopnia n

W ogólnym przypadku otrzymujemy:

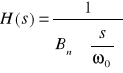
(13)

gdzie B_n(*) jest wielomianem Butterwortha stopnia n. Poniżej podajemy kilka pierwszych wielomianów Butterwortha:

………………………………

…………………….………. (14)

Wielomiany te maja oczywiste właściwości:

(15)

Aproksymacja Butterwortha odznacza się dużą prostotą. Ma także pewne zalety wynikające z monotoniczności charakterystyki amplitudowej. Jej podstawową wadą jest jednak mała selektywność wyrażająca się zbyt słabym rozgraniczeniem pasma przepustowego ω<ω₀ od pasma zaporowego ω>ω₀. Znacznie lepsza selektywność można uzyskać stosując aproksymację Czebyszewa.

4. Projekt filtru cyfrowego.

Wymagania:

f_pass1 = 1200 Hz

f_stop1 = 1550 Hz

f_pr = 4000 Hz

A_pass = 3 dB

A_stop = 40 dB

4.1. Określenie parametrów filtru cyfrowego.

4.2. Wyznaczenie pulsacji granicznych filtru analogowego na podstawie przyjętych pulsacji filtru cyfrowego.

4.3. Projekt filtru analogowego.

4.3.1. Wyznaczenie parametrów unormowanego dolnoprzepustowego filtru analogowego.

4.3.2. Projekt prototypowego filtru dolnoprzepustowego Butterwortha.

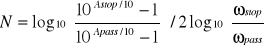
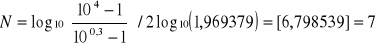
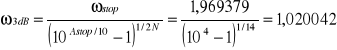
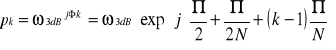
, k=1,2,3,….,N,

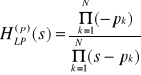
4.3.3. Transformacja częstotliwości filtru prototypowego na filtr określony parametrami w punkcie 4.2.

,

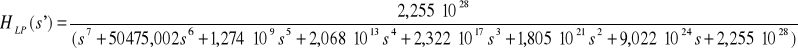
4.3.4. Sprzętowa implementacja zaprojektowanego filtru.

Przyjmujemy wartości: C = 1 nF; R_A=10 kΩ; Rwy = 10 kΩ;

=== Sekcja 1===

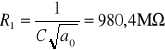
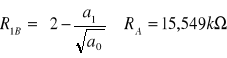
=== Sekcja 2 ===

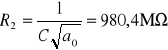
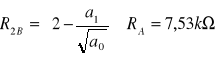
=== Sekcja 3 ===

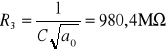
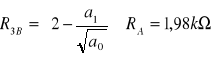
=== Sekcja 4 ===

K₄ =1.

=== Obciążenie ===

K=K₁*K₂*K₃*K₄

K =5.3659935

G=1

Rys.4.1. Schemat układu realizującego filtr dolnoprzepustowy siódmego rzędu z korektą wzmocnienia.

4.4. Wyznaczenie transmitancji filtru cyfrowego na podstawie transformacji biliniowej.

5. Analiza zaprojektowanego układu z wykorzystaniem Scilaba.

5.1. Opis wybranych funkcji Scilaba.

Podstawowe rozkazy grafiki Scilaba :

• driver : wybiera główne okno graficzne.

Następne polecenia są przeznaczone dla zarządzana ekranem :

• xclear : oczyszcza jedno albo kilka okien graficznych;

• xbasc : oczyszcza okno graficzne i wymazuje utworzoną grafikę;

• xpause : przerwa w milisekundach

• xselect : uaktywnia aktualne okno graficzne (dla x - drivers)

• xclick : czeka na kliknięcie myszy.

• xbasr : przerysowuje wykres z okna graficznego

• xdel : usuwa okno graficzne

Różne manipulacje :

Przekształcenia:

• isoview : izometryczna skala bez zmiany okna pozwala na izometryczną skale

w poprzednim oknie wykresu bez zmieniania wielkości okna:

t=(0:0.1:2*%pi)';

plot2d(sin(t),cos(t));

xbasc()

isoview(-1,1,-1,1);

plot2d(sin(t),cos(t));

• square : izometryczna skala ze zmienianiem wielkości okna

wielkość okna jest zmieniana według parametrów polecenia.

• scaling : skalowanie na danych

• rotate : rotacja

scaling i rotate wykonują się kolejno

• xgetech, xsetech : zmiana skali wewnątrz okna graficznego.

Wykresy 2D

Składnia minimum: plot2d(y) - w takiej postaci dostaniemy wykres wartości

znajdujących się w wektorze y, na osi x zostaną umieszczone numery kolejnych wartości y.

Plot2d(x,y) - x i y są wektorami, wynikiem jest wykres punktów o współrzędnych (x,y)

branych kolejno z obu wektorów. Oczywiście oba wektory muszą mieć jednakowe długości

(ale nie jest istotne czy są wierszowe czy kolumnowe). Jeśli y jest macierzą, jego rzędy są

wykreślane.

Większa liczba wykresów - wywołanie analogiczne jak powyżej plot2d(x,y), z tym że x

i y muszą tym razem być macierzami (o jednakowych rozmiarach). Wówczas zostanie

wykreślonych tyle wykresów ile jest kolumn w każdej macierzy - danymi do wykresów będą

odpowiadające sobie numerami kolumny z wektorów x i y. Jeśli chcemy zrobić kilka

wykresów, w których x są jednakowe moglibyśmy wektory x „powielić” i utworzyć z nich

odpowiednio dużą macierz (marnotrawilibyśmy w ten sposób pamięć), albo zapisać polecenie

w postaci: plot2d(x,[y1,y2]) - wówczas wartości x dla wszystkich wykresów zostaną

wzięte z tego samego wektora x. Zapis tu przedstawiony odpowiada sytuacji, gdy y1 i y2 są

wektorami kolumnowymi, w ich miejscu może znaleźć się macierz mająca dwie kolumny (lub

więcej) i oczywiście tyle samo wierszy co wektor (w tym przypadku kolumnowy lub

wierszowy) x (z tym jednak, że jeśli chcemy wykonać wykres wykorzystując wektor x i

macierz y to musimy polecenie zapisać z nawiasami kwadratowymi: plot2d(x,[y]), w

przeciwnym razie dostaniemy komunikat o niedopasowaniu rozmiarów argumentów).

Ogólna postać wykresu 2D:

• plot2di(x,y,< opcjonalne argumenty >) - dobierając odpowiednio

opcjonalne argumenty (w dowolnej kolejności) możemy wpływać na wygląd

wykresu.

• indeks plot2d : i = 1,2,3,4.

Dla różnych wartości i mamy:

i = 1 : liniowe/logarytmiczne kreślenie

i = 2 : wykres, w którym w kolejnych przedziałach wartości są stałe.

i = 3 : wykres słupkowy

i = 4 : poszczególne fragmenty linii (łączące kolejne punkty) są strzałkami.

Dla pojedynczej krzywej wektor może być rzędem albo kolumną:

plot2d(t',cos(t)') plot2d(t,cos(t)) jest równoznaczny.

• opcja style : wektor o długości równej liczbie krzywych, każdy element

odpowiada kolejnej krzywej (w kolejności kreślenia). Jeżeli wartość jest liczbą

dodatnią to kreślona jest linia ciągła lub przerywana o kolorze odpowiadającym

wartości. Jeżeli jest liczbą ujemną (lub zerem) to rysowany jest symbol o numerze

abs(wartość). W szczególnym przypadku jeśli wykreślona jest tylko jedna krzywa,

style może być wektorem dwuelementowym, którego pierwszy składnik ma

11

znaczenie opisane powyżej, a drugi przyjmuje wartość z zakresu 1-6 i oznacza

położenie opisu tej krzywej. Taka opcja jest przydatna, gdy na jednym wykresie

rysuje się większą liczbę krzywych za pomocą osobnych komend plot2d. Jeżeli

wykreślanych jest więcej krzywych, a nie podano wektora style kolejnym

krzywym zostaną przypisane kolejne kolory.

• leg: jest to łańcuch opisów dla różnych krzywych. Jest rozdzielony przez @ : na

przykład `` module@phase" ( zobacz przykład poniżej). Te nagłówki pokazane są

pod wykresem z małymi znaczkami przedstawiającymi styl poszczególnych

krzywych. Jest on aktywny tylko wtedy, gdy strf=1

• rect : jest to 4-o elementowy wektor wartości określający granice osi

rect=[xmin,ymin,xmax,ymax]. Aktywne tylko wtedy, gdy drugi element

strf = 1,3 lub 5

• nax : wektor czteroelementowy określający liczbę podziałów osi [nx,Nx,ny,Ny]

(N -podziały „główne”, n - „podpodziały”). Ma znaczenie tylko, gdy trzeci

element strf wynosi 1).

• logflag - łańcuch dwuelementowy, pierwszy znak dotyczy osi x, drugi - osi y,

każdy może przyjąć wartość "n" („normalna” - równomierna) lub "l"

(„logarytmiczna”). Np. ["nn"] - obie osie równomierne, ["nl"] - oś x równomierna,

oś y logarytmiczna.

5.2. Plik wsadowy programu Scilab.

Poniżej znajduje się program napisany w Scilabie służący do obliczania parametrów filtra analogowego i cyfrowego jak również do wyznaczenia podstawowych charakterystyk.

// Podaj wymagania projektowe

typ = 1; // rodzaj filtra: 1 = LowPass, 2 = HighPass, 3 = BandPass, 4 = BandStop

apass = 3; // nieliniowoœć pasma przepustowego w dB ("zwis")

astop = 40; // tłumienie w paœmie zaporowym

fpr = 4000; // częstotliwoœć próbkowania

fmx = 1000; // maksymalna częstotliwoœć charakterystyki na rysunku

// Podaj częstotliwoœci graniczne

if (typ==1) // FILTR DOLNOPRZEPUSTOWY

fpass = 1200; // częstotliwoœć pasma przepustowego odpowiadajšca Apass

fstop = 1550; // częstotliwoœć pasma zaporowego odpowiadajšca Astop

fpass = 2*fpr*tan(%pi*fpass/fpr)/(2*%pi); // f cyfrowe --> f analogowe

fstop = 2*fpr*tan(%pi*fstop/fpr)/(2*%pi); //

ws = fstop/fpass; // transformacja częstotliwoœci: s=s'/w0, w0=2*pi*fpass

end

// Przelicz decybele na wartoœć bezwzględnš, np. 40 dB = 0.01

wzm_p = 10^(-apass/20);

wzm_s = 10^(-astop/20);

// Oblicz parametry pomocnicze

if( (typ==1) | (typ==2) )

vp = 2*%pi*fpass;

vs = 2*%pi*fstop;

f_ps = [fpass, fstop]; wzm_ps = [wzm_p, wzm_s]; wzmdB_ps = [-apass, -astop];

end

// Oblicz parametry filtra: N i w0

wp = 1;

N = ceil( log10( (10^(astop/10)-1) / (10^(apass/10)-1) ) / (2*log10(ws/wp)) )

w0 = ws / (10^(astop/10)-1)^(1/(2*N))

// Oblicz bieguny transmitancji dolnoprzepustowego filtra prototypowego i jej współczynniki

dfi0 = (2*%pi)/(2*N); // kšt "kawałka tortu"

fi = %pi/2 + dfi0/2 + (0 : N-1)*dfi0; // kšty biegunów

p = w0*exp(%i*fi); // bieguny

z = []; // zera

wzm = real( prod(-p) ); // wzmocnienie

a = poly(p,"a"); // bieguny --> wsp wielomianu mianownika A(z)

b = wzm; // wielomian licznika B(z)

z, p, b, a,

plot( real(p), imag(p), 'x' ); xgrid(4); xtitle('Połozenie biegunów','Real','Imag');

// Oblicz charakterystykę częstotliwoœciowš H(w)=B(w)/A(w)

w = 0 : 0.005 : 2; // zakres pulsacji unormowanej; pulsacja granicy pasma przepustowego = 1

H=buttmag(N,apass,w);

xinit()

xgrid(4);

plot(w,abs(H)); xtitle('Moduł prototypu LPass','pulsacja [rad/sek]'); xgrid(4);

xinit()

plot(w,20*log10(abs(H))); xtitle('Moduł prototypu LowPass w dB','pulsacja [rad/sek]','dB');xgrid(4);

// Transformata częstotliwoœci filtra analogowego: prototyp unormowany --> wynikowy filtr

//////////////////////////////////////LowPass////////////////////////////////////////////////////////////////////////

if (typ==1)then

zz = []; pp = [];

for k=1:length(z)

zz = [ zz z(k)*vp ]; //wyznaczenie macierzy

wzm = wzm/vp;

end

for k=1:length(p)

pp = [ pp p(k)*vp ];

wzm = wzm*vp;

end

end

/////////////////////////////////////// HighPass: /////////////////////////////////////////////////////////////////

if (typ==2) then

zz = []; pp = [];

for k=1:length(z)

zz = [ zz vp/z(k) ];

wzm = wzm*(-z(k));

end

for k=1:length(p)

pp = [ pp vp/p(k) ];

wzm = wzm/(-p(k));

end

for k=1:(length(p)-length(z))

zz = [ zz 0 ];

end

end

///////////////////////////////////////////////////////////////////////////////////////////////////////////////

b=wzm*poly(zz,'s');

a=poly(pp,'s');

printf('\n\n Transmitancja ')

Hs=real(b)/real(a) //obliczenie transmitancji

// Pokaż zera i bieguny po transformacji częstoliwoœci

xinit()

xset("mark size",4);

plot2d( real(zz),imag(zz),style=-4);

plot2d(real(pp),imag(pp),style=-4);

xtitle('Połozenie biegunów po transformacji','real','imag');

xgrid(4);

// Końcowa charakterystyka częstoliwoœciowa

NF = 1000; // ile punktów

fmin = 1; // dolna częstotliwoœć

fmax = 5000; // górna częstotliwoœć

f =fmin : (fmax-fmin)/(NF-1) : fmax; // wszystkie częstotliwoœci

w = 2*%pi*f; // wszystkie pulasacje

xinit();

hf=freq(Hs(2),Hs(3),%i*w);

hm=abs(hf);

xset("mark size",5);

xgrid(4);

plot2d(f,hm,style=5);

plot2d(f_ps,wzm_ps,style=-5);

xtitle('Moduł ','freq [Hz]','dB');

xgrid(4);

xinit();

xset("mark size",5);

plot2d(f_ps,wzmdB_ps,style=-9);

plot2d(f,20*log10(hm),style=5);

xtitle('Modul dB','freq [Hz]');

xgrid(4);

xinit()

plot2d(f',phasemag(hf,'c')');//wykres fazowy

xgrid(4);

xtitle('FAZA','freq [Hz]','[deg]');

xinit()

bode(f,hf);//wykres Bodego

xinit();

nyquist(f,hf)//Wykres Nyquista

// H(s) --> H(z) Transformacja biliniowa

pc = []; zc = [];

for k=1:length(zz)

zc = [ zc (2*fpr+zz(k))/(2*fpr-zz(k)) ];

wzm = wzm*(2*fpr-zz(k));

end

for k=1:length(pp)

pc = [ pc (2*fpr+pp(k))/(2*fpr-pp(k)) ];

wzm = wzm/(2*fpr-pp(k));

end

if (length(pp)>length(zz)) then zc = [ zc -1*ones(1,length(pp)-length(zz)) ]; end

if (length(pp)<length(zz)) then pc = [ pc -1*ones(1,length(zz)-length(pp)) ]; end

gg=1:1700;

bc=wzm*coeff(poly(zc,'s')); ac=coeff(poly(pc,'s'));

bc1=wzm*poly(zc,'s'); ac1=poly(pc,'s');

// Pokaż zera i bieguny filtra cyfrowego

NP = 1000; fi=2*%pi*(0:1:NP-1)/NP; x=sin(fi); y=cos(fi);

//plot(x,y,'-k',real(zc),imag(zc),'or',real(pc),imag(pc),'xb');

//title('ZERA i BIEGUNY filtra cyfrowego'); grid;

// Otrzymana charakterystyka częstotliwoœciowa

NF = 1000; fmin = 1; fmax = 1000; f = fmin : (fmax-fmin)/(NF-1) : fmax;

w =2*%pi*f/fpr;

printf('\n\n Transmitancja ')

Hz=real(bc1)/real(ac1)

xinit()

xset("mark size",4);

H = freq(real(bc),real(ac),%i*w);

Habs=abs(H);// HdB=20*log10(Habs); Hfa=unwrap(angle(H));

xinit();

xset("mark size",4);

hf=freq(Hz(2),Hz(3),%i*w);

xinit()

bode(f,hf);//wykres Bodego

xinit();

nyquist(f,hf)//Wykres Nyquista

f_ps = (fpr/%pi)*atan(%pi*f_ps/fpr);

//

xinit();

xtitle(['Moduł'],'freq [Hz] ',' ');

plot2d(f_ps,wzm_ps,style=3);

xinit();

xtitle(['Moduł dB'],'freq [Hz] ',' ');

plot2d(f_ps,wzmdB_ps,style=3);

xinit();

plot2d(f,hf); xgrid(2);

xtitle(['FAZA'],'freq [Hz]','[rad]');

// OdpowiedŸ impulsowa (filtracja sygnału delty Kroneckera)

Nx=200; x = zeros(1,Nx); x(1)=1;

M=length(bc); N=length(ac);

ac=ac(2:N); N=N-1;

bx=zeros(1,M); by=zeros(1,N); y=[];

for n=1:Nx

bx = [ x(n) bx(1:M-1)];

y(n) = sum(bx .* bc) - sum(by .* ac);

by = [ y(n) by(1:N-1) ];

end

n=0:Nx-1;

xinit();

plot2d(n,y,style=6); xgrid(2);

xtitle(['Odpowiedz impulsowa h(n)'],'n',' ' );

halt();//xlabel('n');

// Oblicz elementy układu ze wzmacniaczami operacyjnymi

p(1), p(2), p(3) , p(4)

halt();

p1 = [ p(1) conj(p(1)) ];

p2 = [ p(2) conj(p(2)) ];

p3 = [ p(3) conj(p(3)) ];

p4 = p(4);

aw1 = poly(p1,'s'), aw2 = poly(p2,'s'), aw3 = poly(p3,'s'), aw4 = poly(p4,'s')

halt();

C = 10^(-9); RA=10^4; Rwy = 10^4;

disp('=== Układ 1===')

a = coeff(aw1);

a2=a(3);a1=a(2);a0=a(1);

R = 1/(C*sqrt(a0))

RB = (2-a1/sqrt(a0)) * RA

K1 = 1+RB/RA

halt();

disp('=== Układ 2 ===')

a = coeff(aw2);

a2=a(3);a1=a(2);a0=a(1);

R = 1/(C*sqrt(a0))

RB = (2-a1/sqrt(a0)) * RA

K2 = 1+RB/RA

halt();

disp('=== Układ 3 ===')

a = coeff(aw3);

a2=a(3);a1=a(2);a0=a(1);

R = 1/(C*sqrt(a0))

RB = (2-a1/sqrt(a0)) * RA

K3 = 1+RB/RA

halt();

disp('=== Układ 4 ===')

a = coeff(aw4);

a1=a(2); a0=a(1);

R=1/(C*a0)

K4=1

halt();

disp('=== Obciążenie ===')

K=K1*K2*K3*K4

G=1

Rx = (K/G)*Rwy

Ry = (G/K)/(1-G/K)*Rx

halt();

5.3. Interpretacja graficzna.

5.3.1. Filtr analogowy.

Rys.5.1. Charakterystyka amplitudowa w skali liniowej filtru prototypowego.

Rys.5.2. Charakterystyka amplitudowa w skali logarytmicznej filtru prototypowego.

Rys.5.3. Położenie biegunów po transformacji filtru prototypowego na filtr docelowy.

Rys.5.4. Charakterystyka amplitudowa w skali liniowej po transformacji filtru prototypowego na filtr docelowy.

Rys.5.5. Charakterystyka amplitudowa w skali logarytmicznej po transformacji filtru prototypowego na filtr docelowy.

Rys.5.6. Charakterystyka fazowa po transformacji filtru prototypowego na filtr docelowy.

Rys.5.7. Charakterystyka Nyquista.

5.3.2. Filtr cyfrowy.

Rys.5.8. Położenie zer i biegunów.

Rys.5.9. Charakterystyka amplitudowa w skali liniowej.

Rys.5.10. Charakterystyka amplitudowa w skali logarytmicznej.

Rys.5.11. Charakterystyka fazowa.

Rys.5.12. Odpowiedź impulsowa.

6. Podsumowanie.

Podstawową cechą, a zarazem zaletą wyróżniającą filtry Butterwortha spośród innych filtrów jest ich brak zafalowań w paśmie przepustowym i zaporowym, co można zaobserwować na charakterystykach częstotliwościowych umieszczonych w naszym projekcie. Przebiegi na charakterystykach amplitudowych „łagodnie” przechodzą z pasma przepustowego w zaporowy bez jakichkolwiek gwałtownych przeskoków czy wahań. Świadczy to o osiągnięciu przez nas zamierzonego celu jakim było zaprojektowanie filtru dolnoprzepustowego, przypominającego jak najbardziej filtr idealny. Negatywną cechą filtrów Butterwortha, zauważalną podczas projektowania jest to, że przebiegi odznaczają się bardzo małymi zboczami pasm przejściowych. Najbardziej jest to widoczne na charakterystykach amplitudowych. Z tego powodu ażeby uzyskać taką samą stromość opadania (jak w innych prototypach filtrów) należy zwiększyć rząd filtru, co wiąże się ze zwiększeniem liczby sekcji przy implementacji sprzętowej.

Obliczenia pokrywają się z przyjętymi założeniami zarówno te uzyskane metodami numerycznymi w programie Scilab jak i obliczeniami własnymi. Wszelkie drobne nieścisłości wynikają jedynie z zaokrągleń. Znikoma różnica między nimi jest do pominięcia, gdyż nie ma wpływu na zmianę parametrów.

Dużą część czasu poświęconego na pracę nad projektem pochłonęło nam napisanie pliku wsadowego w programie Scilab. Co prawda mięliśmy gotowy plik napisany w programie Matlab jednak ze względu na znaczne różnice pomiędzy tymi programami, zadanie nie było łatwe do wykonania. Dzięki stworzeniu tego pliku w Scilabie mogliśmy uzyskać charakterystyki, które w sposób jasny obrazują charakter filtru. Pozwala on też na szybkie i przejrzyste przeanalizowanie filtru o danych parametrach. Uniwersalność naszego pliku wsadowego pozwala na obliczenia części analogowej, cyfrowej jaki i realizację sprzętową. Jednak w części cyfrowej programu Scilab napotkaliśmy na pewien problem związany z tworzeniem charakterystyk częstotliwościowych. Otóż ze względu na ograniczenia programowe, Scilab przedstawia charakterystyki tylko w zakresie ich opadania tj. pomiędzy zakresem przepuszczania a zaporowym, co uniemożliwia nam obejrzenie okresowości przebiegu w dziedzinie częstotliwości. Tej wady pozbawiony jest Matlab, który generuje charakterystyki w dowolnym zakresie częstotliwości. Dlatego też, w rozdziale 5.3.2 umieściliśmy charakterystyki pochodzące z programu Matlab.

Jak już wspominaliśmy, Scilab pomógł nam w wyliczeniu elementów służących do realizacji sprzętowej zaprojektowanego filtru. Polegało to na założeniu pewnych wartości dowolnych pozostałe natomiast wyliczył program na podstawie wzorów. Większość wyznaczonych wartości elementów nie należą do tzw. typoszeregu dostępnego w sklepach RTV i z tego powodu muszą być zastąpione „najbliższymi” wartościami, które są w sprzedaży. Wykaz poszczególnych elementów a także schemat układu elektronicznego realizującego nasz filtr przedstawione są w projekcie. Nie jest to jakiś skomplikowany układ dlatego też, zbudować go może osoba, która choć trochę orientuje się w elektronice.

7. Literatura.

1. T. Zieliński: „Od teorii do cyfrowego przetwarzania sygnałów”, AGH Kraków, 2002r.

2. L. Gołębiowski, M. Gołębiowski: „Obwody elektryczne cz. II i III.” O.W.PRz., Rzeszów 2004.

3. J. Bajorek, L. Gołębiowski, W. Posiewała: „Obwody elektryczne - laboratorium mikrokomputerowe. O.W.Prz., Rzeszów 1996.

4. S. Bolkowski, W. Brociek, H. Rawa: „Teoria obwodów elektrycznych - zadania” W.N.T., Warszawa 1995.

---