Elementy krystalografii (dział nauki zajmujący się opisem, klasyfikacją i badaniem kryształów, krystalitów oraz substancji o strukturze częściowo uporządkowanej)

Kryształy wykazują ciekawą właściwość, tzw. anizotropię, polegającą na uzależnieniu właściwości fizycznych od kierunku, w którym się je bada. W pewnych kierunkach elementy strukturalne mogą być z sobą związane słabiej niż w innych. Wówczas kryształ wykazuje zmniejszoną wytrzymałość mechaniczną i łatwo daje się łupać wzdłuż pewnych płaszczyzn, przy czym próba nie powiedzie się przy uderzeniu wzdłuż płaszczyzny do niej prostopadłej.

Oprócz anizotropii mechanicznej, różne wartości dla różnych kierunków może wykazywać współczynnik załamania światła, współczynnik sprężystości, współczynnik rozszerzalności liniowej, przewodnictwo cieplne, przewodnictwo elektryczne, względna przenikalność elektryczna (stała dielektryczna) i inne. Ciała bezpostaciowe są izotropowe, tzn. we wszystkich kierunkach mają identyczne właściwości mechaniczne, optyczne i elektryczne, podobnie jak w gazach i w cieczach.

Monokryształ: materiał będący w całości jednym kryształem (np. kryształ cukru, soli)

Polikryształ: ciało stałe będące zlepkiem wielu monokryształów, zwanych ziarnami. (np. polikrystaliczny kwarc i piryt)

Bardzo często mamy do czynienia z substancjami polikrystalicznymi rzadko monokryształami

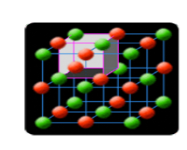
Kryształ: ciało posiadające trójwymiarowe periodyczne uporządkowanie atomów, jonów lub molekuł, z których kryształ jest zbudowany.

Komórka elementarna powtarza się we wszystkich trzech kierunkach, tworząc zamkniętą sieć przestrzenną, której główną cechą jest symetria. Komórka elementarna ma zawsze kształt równoległościanu. Poprzez translacje komórki elementarnej o wektory będące całkowitymi wielokrotnościami wektorów sieci krystalicznej otrzymuje się całą sieć krystaliczną kryształu.

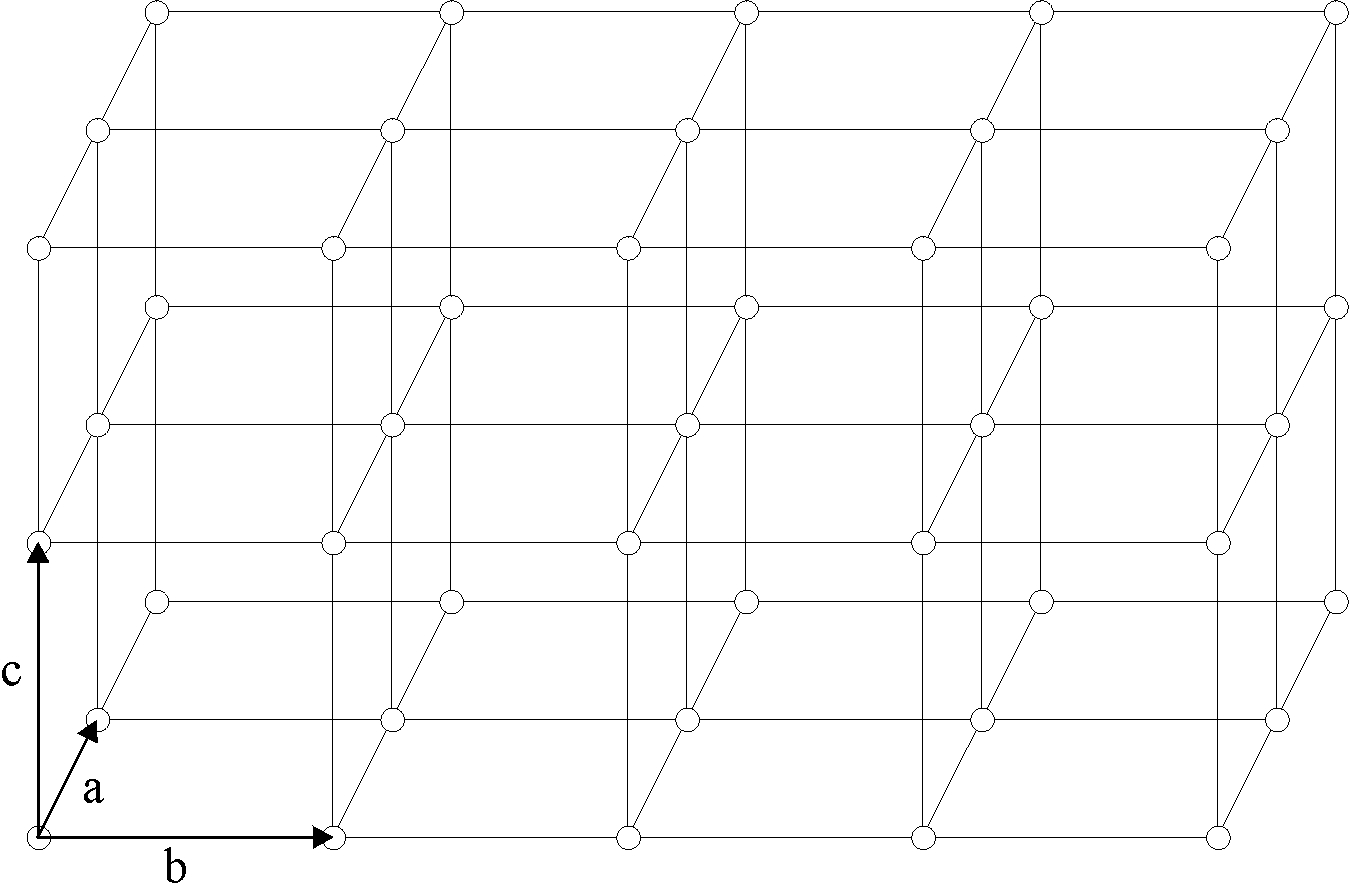
W krystalografii (a, b, c) są nazywane stałymi sieciowymi lub parametrami sieciowymi. Układ współrzędnych przyjmuje się w ten sposób, aby oś x leżała wzdłuż krawędzi a, oś y - wzdłuż krawędzi b, a oś z - wzdłuż krawędzi c. Relacja między kątami i krawędziami jest następująca: kąt α jest między krawędzią b i c, kąt β między a i c i kąt γ między a i b.

Powtarzanie komórki elementarnej - ściana do ściany - w trzech wymiarach tworzy całą strukturę krystaliczną. Podstawową cechą komórki elementarnej jest to, że reprezentuje ona w pełni całą strukturę krystaliczną.

Oprócz parametrów sieci a, b i c; α, β i γ strukturę krystaliczną charakteryzują:

• Liczba najbliższych sąsiadów, zwana liczbą koordynacyjną,

• Odległość między najbliższymi atomami w krysztale,

• Liczba atomów w komórce elementarnej,

• 
  
  Współczynnik upakowania, czyli stosunek objętości kryształu zajętej przez atomy (traktowane jako „kulki”) do całkowitej objętości kryształu.

Komórka elementarna prosta: (P) jeden atom przypada na jedną komórkę elementarną. Atomy w narożach komórki

Komórki centrowane: przestrzennie (I) i płasko (F)

Poprzez translacje komórki elementarnej o wektory będące całkowitymi wielokrotnościami wektorów sieci krystalicznej otrzymuje się całą sieć krystaliczną kryształu.

Translacja: to izometria polegająca na równoległym przesunięciu figury, zbioru lub innego zwykle geometrycznego obiektu o pewien ustalony wektor na prostej, płaszczyźnie, w przestrzeni euklidesowej lub na dowolnej innej rozmaitości. Translacja nie zmienia kształtu figury ani żadnych wewnętrznych relacji pomiędzy jej elementami, natomiast zmienia położenie figury w stosunku do innych (nie podlegających translacji) figur.

(Kryształ ciało posiadające trójwymiarowe periodyczne uporządkowanie atomów, jonów lub molekuł, z których kryształ jest zbudowany)

Uporządkowanie te daje się stosunkowo prosto opisać przez podanie własności symetrii. Symetrię kryształu definiuje się poprzez podanie operacji symetrii przekształcających kryształ sam w siebie. Przekształceniami symetrii są: translacje, obroty, inwersja, obroty inwersyjne i płaszczyzny odbicia.

Opis struktur krystalicznych za pomocą komórek elementarnych jest bardzo dogodny, gdyż wszystkie możliwe struktury zostają zredukowane do siedmiu różniących się kształtem komórek elementarnych, których powtarzanie - ściana do ściany - wypełnia ściśle trójwymiarową przestrzeń. Są one nazywane siedmioma układami krystalograficznymi

Komki elementarne charakteryzuje sześć parametrów sieci:

Okresy identyczności sieci: a, b, c

Kąty: α, β, γ

Tworzą one równoległościan elementarny

a=b=c, α=β=γ=90⁰ a=b≠c, α=β=γ=90⁰ a=b≠c α=β=90⁰ γ =120⁰ a=b=c α=β=γ≠90⁰

układ regularny układ tetragonalny układ heksagonalny układ trygonalny

Oś symetrii: dana figura (częśc figury) powtarza się n razy przy obrocie wokół pewnej prostej stale o ten sam kąt (mieszczący się całkowitą liczbę n razy w 360 ⁰ ) n=360⁰ C nazywa się krotnością osi

Środek symetrii (inwersja) - w jednakowej odległości wzdłuż dowolnej prostej przechodzącej przez środek symetrii znajdują się jednakowe części figury (jednakowy motyw)

Płaszczyzna symetrii: dwie figury (lub części jednej figury) pozostają względem siebie w takim stosuku jak przedmiot do swego obrazu w płaskim zwierciadle

---