ROZWIĄZYWANIE MAŁYCH TRÓJKĄTÓW SFERYCZNYCH

Met. Legendre'a

Koło wielkie - ślad przecięcia płaszczyzny sfery płaszczyzną przechodzącą przez jej środek

Trójkąt sferyczny - powstaje z przecięcia trzech kół wielkich

Trójkąt biegunowy - wierzchołki trójkąta sferycznego są biegunami boków trójkąta biegunowego i odwrotnie.

Trójkąt sfer. o małych bokach (ok. 30km) może być rozwiązany jak 3kąt płaski o bokach takiej samej dł. jak boki w 3kącie sfer. i kątach równych kątom 3kąta sfer. zmniejszonym o 1/3 ekscesu sferycznego.

Moszna zastosować tw. sinusowe

3kąta płaskiego:

Met. Soldnera (additamentów)

Mały 3kąt sfer. może być rozwiązany tak jak 3kąt płaski, w którym kąty będą te same, a boki zostaną zmniejszone o odpowiednie wielkości.

Additamenty są wielkościami

obliczanymi w oparciu o wzory:

Dalej rozwiązujemy 3kąt tak jak 3kąt płaski, stosując tw. sinusowe:

WSPÓŁRZĘDNE ELIPSOIDALNE (geodezyjne)

Równoleżnik - ślad przecięcia elipsoidy płaszcz. przechodzącą przez dany p-kt i równoległą do płaszcz. równika.

Południk - ślad przecięcia elipsoidy płaszcz. przechodzącą przez oś obrotu elipsoidy

Elipsoida obrotowa definiowana jest parametry określające jej kształt i wielkość: duża półoś a i mała półoś b, spłaszczenie α oraz mimośród e2. Zależności między parametrami: α=(a-b)/a, e2=(a2-b2)/a2,

e2= α(2- α), e'2=e2/(1-e2).

Współrzędne elipsoidalne:

L-długość geodezyjna-kąt dwuścienny między płaszczyzną południka 0˚a południkiem przechodzącym przez dany punkt.

B-szerokość geodezyjna-kąt między normalną do elipsoidy w punkcie P a płaszczyzną równika.

Przeliczanie współrzędnych:

X = U cosL Y = U sinL,

SZEROKOŚĆ ZREDUKOWANA

  kąt między promieniem kuli przechodzącym przez punkt P₁ (będący rzutem na sferę o promieniu b punktu P), a płaszczyzną równika.

z = b sin ; P₃ = b

Kąt  można zdefiniować przez rzutowanie p-ktu P wzdłuż promienia równoleżnika na sferę o promieniu b. Rzut p-ktu P na sferę ma wsp. geograficzne , L.

SZEROKOŚĆ GEOCENTRYCZNA

ρ - kąt między prostą przechodzącą przez punkt P i środek elipsoidy a płaszczyzną równika.

tg ρ = (1-e²) tgB

PRZEKROJE NORMALNE

są to przekroje płaszczyzną zawierającą sobie normalną do powierzchni w danym punkcie. Wyróżnia się 2 przekroje główne: przekrój południkowy elipsoidy obrotowej płaszczyzną południka o minimalnym promieniu krzywizny M oraz przekrój poprzeczny płaszczyzną prostopadłą do południka o maksymalnym promieniu krzywizny N.

Krzywizna przekroju południkowego:

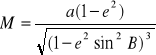
Krzywizna przekroju poprzecznego:

Średni promień krzywizny w punkcie:

Przeliczanie współrzędnych:

X = N cosB cosL Y = N cosB sinL

Z = N (1-e²) sinB

q=Ne²*sinB

B = arctg((Z+q)/pierw(X²+Y²))

L = arccos(X/pierw(X²+Y²))

Δr=r-NcosB

h = pierw(Δr²+Δz²), Δr=r-NcosB, r=pierw(X²+Y²) Δz=z-N(1-e²)sinB

Promień krzywizny dowolnego przekroju normalnego:

1/R_A = sin²A / N + cos²A / M, A - azymut

Wzajemne przekroje normalne: jeżeli w punkcie P₁ poprowadzimy przekrój normalny przechodzący przez punkt P₂, a przez P₂ przekrój normalny przechodzący przez P₁ to przekroje te będą wzajemnie normalne, których wzajemne położenie określają kąty ω₁ i ω₂ oraz ich maksymalna odległość na powierzchni elipsoidy.

Linia geodezyjna - jest to krzywa, charakteryzująca się tym, że i normalna główna w każdym jej punkcie jest jednocześnie normalną do danej powierzchni. Płaszczyzna ściśle styczna w każdym punkcie linii geodezyjnej zawiera normalną do powierzchni w tym punkcie.

Pow ekwipotencjalna - to pow jednego potencjału (każdy pkt posiada potencjał jednakowej wartości) W każdym pkt pow ekipo. Wektor przyśpieszenia g jest prostopadły do pow ekwipotencjalnej dlatego pow te nazywamy pow poziomymi (pow ekipo. Nie są powierzchniami równoległymi, nie przecinają się i są zamknięte, przez co są krzywymi zwróconymi wklęsłością do osi obrotu Ziemii. W(xyz)=const

Twierdzenie Clairauta:

Iloczyn promienia równoleżnika i sinusa azymutu linii geodezyjnej w każdym jej punkcie jest wielkością stałą;

r₁ sinA₁ = r₂ sin A₂ = const

Wzór Somigliana: γa - normalne przyśpieszenie siły ciężkości na równiku γb - normalne przyśpieszenie siły cieżkości na biegunie elipsoidy a,b - półosie elipsoidy B - szer geoid

Geoida - pow ekwipotencjalna która zawiera w sobie swobodny poziom mórz i oceanów. Przedstawia prawdziwy kształt ziemii

Promień krzywizny przekroju południkowego M w punkcie P o szerokości geod. B

M=a*(1-e²)/(1-e²*sin² B)^3/2 Jest to promień krzywizny głównego przekroju normalnego (elipsy południkowej) w punkcie P(B,L)

Promień krzywizny poprzecznego przekroju głównego N obliczamy:

N=r/cos=a/(1-e²*sin² B)^½

W biegunach elipsoidy (B=+/-90º) - promienie krzywizn wszystkich przekrojów normalnych są sobie równe: N=M=a/(1-e²)½

Krzywiznę k w punkcie P charakteryzuje średni promień krzywizny obliczony na podst. wzoru: Q=(MN)½=a(1-e²)/1-e²sin²B - śr. Promień gaussowski

Krzywizna: k=1/MN=1/Q² - krzywizna Gaussowska

Promień przekroju dowolnego Ra= N/1+e²*cos²B*cos²A

Kąt A jest kątem dwuściennym (azymutem) między płaszczyznami przekroju południkowego i płaszczyzną przekroju dowolnego.

Długość linii geodezyjnej:

Do 60km: S = Ms(B1-B2), Ms = M(Bśr)

60-750km: S = (M1+4Ms+M2 / 6 * (B2-B1)

Pow. 750km: S = całka(od B1 do B2) MdB

Metoda Clarka - obliczanie współrzędnych końca linii geodezyjnej,

długości linii geodezyjnej i azymutu końca linii.

1) poprowadzenie prostopadłej do południka danego punktu P1 przechodzącą przez szukany punkt P2, uzyskując punkt pomocniczy C. Trójkąt P1P2C rozwiązujemy na kuli o promieniu równym średniemu promieniowi krzywizny w punkcie P1. Obliczamy nadmiar sferyczny:

ε = (s₁₂²sinA₁₂cosA₁₂) / (2MN)

2) Dla punktu P1 z TW sinusów dla trójkąta płaskiego obliczamy u i v:

u = s₁₂ cos(A₁₂ - 2/3 ε) v = s₁₂ sin(A₁₂ - 1/3 ε)

[Bs = B₁ + (1/2*u)/(M₁)]

3) Dla punktu C w połowie odcinka u obieramy punkt S: B_C = B₁ + u/M_S.

[M_c ,N_c]

4) Przez punkty leżące na równoleżniku punktu P2 prowadzimy normalne. Punkty C1, P2 i Bn rzutujemy na kulę o promieniu N₂, której środek znajduje się w punkcie O₂. Obliczamy szerokość geodezyjną B₂:

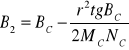
5) Obliczamy nadmiar sferyczny w trójkącie biegunowym ω: ω = B_C - B₂, a potem przyrost długości geodezyjnej:

L₂ = L₁ + ΔL

6) Obliczamy γ z TW sinusów dla trójkąta płaskiego: γ = ΔL sin(B₂+2/3 ω)

7) A₂₁ = 270 + γ - (90 + ε - A₁₂)

UKŁADY WSPÓŁRZĘDNYCH W GEODEZJI:

Konwencjonalny Układ Ziemski: [ CT ]

1)początek układu w środku mas Ziemi

2)oś podstawowa z - średnia oś obrotu

3)oś drugorzędna x - przecięcie płaszczyzny średniego równika z płaszczyzną średniego południka Greenwich

4) oś trzeciorzędna y w układzie ortogonalnym prawoskrętnym

Lokalny Układ Współrzędnych Astronomicznych: [ LA ]

1)środek układu w punkcie P

2) oś podstawowa z - normalna do powierzchni poziomej w punkcie P (Wp=const)

3)oś drugorzędna x - północny kierunek stycznej do powierzchni ekwipotencjalnej w punkcie P w płaszczyźnie południka astronomicznego

4)oś trzeciorzędna y - ortogonalna w układzie lewoskrętnym.

Współrzędne astronomiczne Φ-szerokość, Λ-długość. Są one określone przez normalną do powierzchni ekwipotencjalnej oraz kierunek osi obrotu Ziemi. Można je wyznaczyć z pomiarów. Płaszczyzna południka astronomicznego punktu P definiowana jest przez wektor g w punkcie P (normalna do pow ekwip) i prostą równoległą do osi obrotu Ziemi przechodzącą przez P (kierunek osi Z). Trzecią współrzędną(W) jest wartość potencjału, której nie można określić w drodze bezpośredniego pomiaru. Wyznacza się różnicę potencjałów względem powierzchni geoidy.

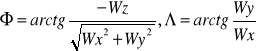
Globalny Układ Geodezyjny [ G ]

1)początek w środku geometrycznym geoidy

2)oś podstawowa z -oś obrotu elipsoidy

3)oś drugorzędna x - przecięcie płaszczyzny równoległej do płaszczyzny średniego równika z płaszczyzną średniego południka Greenwich

4)oś trzeciorzędna y - ortogonalna w układzie prawoskrętnym

Układ ten związany jest z elipsoidą GRS-80 (Geocentryczny Układ Odniesienia)

Lokalny Układ Geodezyjny: [ LG ]

1)środek w punkcie P

2)oś podstawowa z - normalna do elipsoidy w punkcie P

3)oś drugorzędna x - północny kierunek prostopadły do osi z w płaszczyźnie południka geodezyjnego punktu P

4)oś trzeciorzędna y - ortogonalna w układzie lewoskrętnym

Współrzędne geodezyjne B-szerokość,

L-długość, określone są przez normalną do elipsoidy (kierunek wektora γ) oraz kierunek osi obrotu elipsoidy.

Płaszczyzna południka geodezyjnego punktu P zdefiniowana jest przez wektor γ w punkcie P oraz prostą przechodzącą przez punkt P równoległą do osi obrotu elipsoidy.

X = N cosB cosL Y = N cosB sinL

Z = N (1-e²) sinB

ZEWNETRZNE POLE GRAWITACYJNE ZIEMI - na punkt P o jednostkowej masie m=1, znajdujący się w zewnętrznym polu grawitacyjnym Ziemi działa siła przyciągania oraz siła odśrodkowa, prostopadła do osi obrotu Ziemi. Wypadkową tych sił jest siła ciężkości, której przyspieszenie w danym punkcie wynosi:

Gdzie G-stałą grawitacji, M-masa Ziemi,

ω-prędkość kątowa ruchu wirowego,

ρ-odległość od osi obrotu

Zewnętrznym polem grawitacyjnym nazywamy przestrzeń otaczającą Ziemię wraz z jej powierzchnią, w której na każdy punkt P działa siła ciężkości. Pole to nie jest stacjonarne, siła ciężkości w danym punkcie jest zmienna w czasie.

Potencjał siły ciężkości - pole grawitacyjne opisuje się funkcją skalarną zwaną potencjałem siły ciężkości lub potencjałem grawitacyjnym, której pochodne cząstkowe są równe trzem składowym wektora siły ciężkości g. Potencjał ten można podzielić na potencjał siły przyciągania i potencjał siły odśrodkowej, który w sumie daje potencjał grawitacyjny:

Grad(w)=(gx, gy, gz) = g

Model pola siły ciężkosci - pow. ekwipotencjalne również geoida, pomimo kształtu zbliżonego do elipsoid obrotowych nie dają się przedstawić w postaci wzorów matematycznych. Model pola siły ciężkości Ziemi zadany jest przez geocentryczną elipsoidę obrotową o parametrach a - duża półoś elipsy, α - spłaszczenie elipsoidy. Z uwagi na to, że pole siły ciężkości jest sumą efektów grawitacji i obrotu Ziemi, do geom parametrów modelu tego pola należy dodać jeszcze 2 parametry fizyczne: M - cała masa Ziemi, w - prędkość kątowa obrotu Ziemi. Parametry te są zdefiniowane jako geodezyjny model odniesienia GRS 1980. Powierzchnia tak zdefiniowanej elipsoidy - elipsoida normalna - jest pow. ekwipotencjalną pola siły ciężkości generowanego przez tą obracającą się z prędkością kątową w elipsę o jednakowej maise M. Zdefiniowane jest również zew. Pole siły ciężkości zwane polem siły ciężkości o potencjale U.

Przyśpieszenie ciężkości (siły ciężkości) g - na każdy punkt materialny o masie m znajdujący się nad Ziemią lub na jej powierzchni działa siła przyciągania Ziemi, oraz siła odśrodkowa, skierowana prostopadle do osi obrotu. (jeżeli masa punktu jest jednostkowa m=1 to pojęcie siła i przyśpieszenie siły są sobie równoważne) Wypadkową tych sił nazywamy siłę ciężkości g = F + Q; gdzie: g - przyśpieszenie siły ciężkości; F - siła przyciągania Ziemi działająca na punkt o masie 1; Q - siła odśrodkowa w tym punkcie

Jednostki: 1cm/s^2 = 1 gal (gl) ; 10-3 cm/s^2 = 1 miligal (mgl) ; 10-6cm/s^2 = 1mikrogal (μgl)

F = ; gdzie G - stała grawitacji wyznaczona doświadczalnie ; M - masa ; r - promień

Q = w^2 * ρ; gdzie w - prędkość kątowa Ziemi ; ρ - odległość od osi obrotu

RÓWNANIE Laplace'a i Poissona:

Pierwsze pochodne potencjału grawitacyjnego są równe składowym wektora przyspieszenia (j/w). Różniczkując te składowe otrzymuje siędrugie pochodne, których suma równa się:

Zω² dla punktów z zewnętrznym polu graw

-4πGσ+Zω² wewnątrz Ziemi

Elementy geometrii pola siły ciężkości

Pole siły ciężkości może być geometrycznie przedstawione w postaci rodziny powierzchni ekwipotencjalnych oraz rodzinę linii pola - linii pionu, których kierunek jest zadany przez kierunek wektora siły ciężkości g. Są to linie prostopadłe do powierzchni ekwipotencjalnych (krzywe przestrzenne, do których wektor g jest styczny).

Wysokość ortometryczna jest mierzona wzdłuż linii pionu od punktu na powierzchni Ziemi do punktu geoidy.

Kierunek wektora przyspieszenia siły ciężkości można wyznaczyć jako prostopadły do płaszczyzny stycznej do spoziomowanej libelli. Libella określa powierzchnię ekwipotencjalną w danym

punkcie. Powierzchnie ekwipotencjalne nie są wzajemnie równoległe, przez każdy punkt przechodzi tylko jedna powierzchnia ekwipotencjalna.

Metoda średniej szerokości Gausa

B=(B1+B2)/2; L=(L1+L2)/2;

ΔL=L2-L1; ΔB=B2-B1; M; N; p=∆B”/(1)*{1+C(3)+D(4)} q=∆B”/(2)*{1+(S/24)-D(5)} S_1-2=pierw(p²+q²); A_sr=arctg(q/p); ΔA=∆L”*sinB*{1+C(6)+d(7)};

A_1-2= A_sr - ∆A/2; A₂₁=A_sr+∆A/2±180°; M1; MS; M2; S_m=((M₁+4*M_S+M₂)/6)* ΔB;

η=(e' )² cos² B; v² = 1+η²; (1) = ρ^" /M;

(2)=ρ^" /N; (3) = (3* tg²B + 2η² + 2)/24;

(4) =η2* (tg² B -4η² tg² B - η² - 1)/8v⁴

(5) = (1 + η² - 9η² tg² B)/24v²

(6) = v²/12; (7) = (3 +8 η² + η⁴)/24v⁴

C = [(ΔL^" cosB)/ρ"]² ; S = [(ΔL^" sinB)/ρ"]²

D = (ΔB^"/ρ")²

UKŁAD „1942”

Współrzędne w odwzorowaniu Gaussa-Krugera .

a) odwzorowanie: równokątne, poprzeczne, walcowe; b) odwzorowanie elipsoidy obrotowej na pobocznicę walca; c) obrazem południka środkowego danego pasa jest odcinek linii prostej, a obrazami pozostałych południków są linie krzywe rozłożone symetrycznie względem obrazu południka środkowego; d) południk środkowy odwzorowuje się bez zniekształceń. Układ współrzędnych: Elipsoida obrotowa Krasowskiego: a) oś OX pokrywa z obrazem południka środkowego; b) oś OY pokrywa się z obrazem równika; c) pasy trzystopniowe; d) pasy sześciostopniowe: λ0 = 15° i λ0 = 21°

Odwzorowania:

1) azymutalne, walcowe, stożkowe; 2) normalne, ukośne, poprzeczne; 3) wiernokątne, wiernoodległościowe, wiernopolowe; 4) styczne, sieczne

Odwzorowanie quasistereograficzne:

a) odwzorowanie: równokątne, normalne, azymutalne; b) odwzorowanie kuli na płaszczyznę. Płaszczyzna nie jeststyczna do kuli tylko sieczne; c) występuje niewielkie zniekształcenie w pobliżu punktu głównego odwzorowania; d) odwzorowanie to jest szczególnie przydatne do przedstawienia obszarów których granice zbliżone są do okręgów; e) punkt główny - P0(B0, L0) powinien znajdować się w pobliżu środka odwzorowanego obszaru; f) południk przechodzący przez punkt główny to południk środkowy; g) południk środkowy odwzorowuje się jako odcinek linii prostej

UKŁĄD 1965

a) początek układu znajduje się w obrazie punktu głównego; b) oś OX skierowana na północ pokrywa się z obrazem południka środkowego; c) oś OY jest prostopadła do niej i tworzy z osią OX układ prostokątny

układ 1965 - składa się z 5 stref odwzorowawczych. W 4 zastosowano odwzorowanie quasistereograficzne (I - IV), natomiast w jednej odwzorowanie Gaussa - Krugera (V). W każdej strefie obliczone są współrzędne prostokątne płaskie. Linie siatki współrzędnych (ΔX=40km;ΔY=64km) dzielą każdą układu na tzw sekcje podziałowe (1:100 000). Sekcje znajdujące się w jednym pionie to słupy numerowane z zach na wsch. Natomiast sekcje znajdujące się na jednym poziomie to pasy numerowane z północy na południe. Każdą sekcję oznacza się liczbą 3 cyfrową: 352 godło sekcji podziałowej (1: 100 000) gdzie (3) - numer strefy, (5) - numer pasa, (2) - numer słupa

Pasy trzystopniowe w odwzorowaniu Gaussa - Krugera:

(rysunek) Pasy nachodzą się na siebie. Jest to tzw zakładka 20km (podwójne współrzędne). Pierwszą elipsoidą odniesienia była elipsoida Bessela z punktem przyłożenia w Borowej Górze. Zastąpiono ją elipsoidą Krasowskiego z punktem przyłożenia w Pułkowie.

Pasy sześciostopniowe w odwzorowaniu Gaussa - Krugera - do opracowań map topograficznych w skalach od 1:10 000 do 1:500 000 przyjęto odwzorowanie Gaussa - Krugera w pasach sześciostopniowych. Obszar Polski mieści się na dwóch pasach południkowych. Pas o południku osiowym λ0 = 15° ma numer 3, a pas o południku osiowym λ0 = 21° ma numer 4. Pasy te pokrywają się odpowiednio z sześciostopniowymi pasami południkowymi nr 33 i 34 Międzynarodowej Mapy Świata w skali 1:1 000 000

Współrzędne cechowane:

X=x; Y = n*1 000 000 + 500 000 + y, gdzie n - cecha danego pasa n=; PASY: a) szczeciński Y=5500 000,00 , b) bydgoski Y=6500 000,00 , c) warszawski Y=7500 000,00 , d) białostocki Y=8500 000,00

SYSTEMY WYSOKOŚCI

a) wysokość normalna - odległość punktu A od quasigeoidy; b) wysokość ortometryczna - odległość punktu A od geoidy; c) wysokość elipsoidalna - odległość punktu A od elipsoidy; d) anomalia wysokości - odległość geoidy od elipsoidy

System wysokości normalnych - powierzchnią odniesienia jest quasigeoida zawierająca w sobie poziom Morza Bałtyckiego

System wysokości ortometrycznych - powierzchnią odniesienia jest geoida (powierzchnia ekwipotencjalna zawierająca w sobie swobodny poziom mórz i oceanów)

WYSOKOSC ORTOMETRYCZNA I POPRAWKA - wysokość ortometryczna H punktu A jest to odległość tego punktu od geoidy jako powierzchni morza mierzona wzdłuż linii siły ciężkości: H= ;gdzie: W0 - potencjał na geoidzie ; WA - potencjał w punkcie A ; g- średnia wartość przyśpieszenia na odcinku H

Poprawka ortometryczna:

P0 = * H+ * H- (Hi,i-1*Δgi)

H = HA = HB = 1 - ; gdzie: δ - gęstość w okolicy ciągu; δm - średnia gęstość skorupy Ziemi = 5,52 g/cm^3 ; HA i HB - wysokość z niwelacji (bez poprawek); R - średni promień ziemi 6370 000m ; Hi,i-1 = ½(Hi + Hi-1) ; Δgi = gi - gi-1 ; g - średnia wartość przyśpieszenia g=; m=4/3*ΠR^2*δm

WYSOKOSC NORMALNA I POPRAWKA - wysokość normalną H liczymy wzdłuż linii pionowej od quasigeoidy do danego punktu H= ; gdzie W0 - potencjał na quasigeoidzie; WA - potencjał w punkcie A; γ- przyśpieszenie normalne w środkowym punkcie na linii pionowej między quasigeoidą a punktem A

Poprawka normalna:

Pn = (γ- γ)*Hśr + (g0 - γ0) Δhi ; gdzie: γ - przyśpieszenie normalne; γ0(B)=978,038 (1+ 0,005302 (sinB)^2-0,000007 (sinB)^2 ; γśr = γ0(Bśr) - 0,1543Hśr ; Hśr = 1/2 (HA + HB) ; (g0 - γ0)śr= ; Δhi = hi - hi-1 ; g0=g + Sgf gdzie: Sgf = 0,308*Hśr

WYSOKOSC DYNAMICZNA I POPRAWKA - jeżeli we wzorze na wysokość normalną w miejsce przyśpieszenia normalnego w środkowym punkcie na linii pionowej między quasigeoidą a punktem A (γ) przyjmiemy wartość przyśpieszenia normalnego na elipsoidzie dla B=45° (γ) to otrzymamy wysokość dynamiczną punktu A

Wysokość dynamiczna - H= ; poprawka dynamiczna: Pd = *Δhi ; γ= γo(45°) ; Δhi= hi - hi-1 ; gi,i-1 = 1/2 (gi + gi+1)

Metoda Schreibera - metoda ta stosowana przy pomiarze kątów poziomych triangulacji głównej. Zaletą tej metody jest wysoka dokładność. Program obserwacji ułożony jest według następujących założeń: a) kąty na danym stanowisku mierzone są we wszystkich kombinacjach, b) pomiar każdego kąta wykonywany jest na innym miejscu limbusa, c) waga kąta wyrównanego równa się 12 a kierunku wyrównanego 24

Program obserwacji: 1) ilość kierunków n, 2) ilość kątów do pomierzenia n-1, 3) ilość grup kątów niezależnych: a) n jest parzyste G = n-1 , b) n jest nieparzyste G = n; 4) ilość kątów w grupie: a) n jest parzyste n/2 , b) n jest nieparzyste ; 5) ilość serii S = 24/n , 6) między seriami limbus powinien być przestawiony o kąt σ = , 7) ilość przestawień limbusa S*(n-1), 8) przy przejściu od pomiarów z jednej grupy do drugiej limbus przestawiamy o kąt: a) n jest parzyste δ = , b) n jest nieparzyste δ = ; 9) wielkość przesunięcia mikrometru μ = w/s gdzie w - wartość mikrometru

Kryteria dokładności:

1) różnica dwóch koincydencji dla jednego nacelowania wynosi 3cc, 2) różnica pomiędzy półseriami danej serii wynosi 12cc, 3) różnica pomiędzy seriami danego kąta max wynosi 12cc, 4) odchylenie wartości kątów obliczonych z poszczególnych serii od wartości kątów wyrównanych na stanowisku max wynosić może 9cc

---