Politechnika Lubelska	Laboratorium Miernictwa Elektrycznego
w Lublinie	Ćwiczenie Nr 3
Imię i nazwisko: Piotr Jurek & Tadeusz Klukowski		Semestr V	Grupa ED 5.1	Rok akad. 1998/99
Temat ćwiczenia: Sprawdzanie wieloukładowych mierników magnetoelektrycznych			Data wykonania 29.10.98	Ocena

Celem ćwiczenia było zapoznanie się z budową i zasadą działania oraz metodami wyznaczania klasy mierników magnetoelektrycznych.

1. Sprawdzanie woltomierza magnetoelektrycznego na zakresie 60mV:

Schemat układu pomiarowego:

Przyrządy użyte do pomiaru:

Z - zasilacz napięcia stałego KB-6118 PL-T-4147-EZ-M;

R_d - opornik dekadowy; DR6-16 nr PL-P3-305-E6;

R - opornik suwakowy o rezystancji 2170Ω 0,18A PL-K025/E6;

mV_w - miliwoltomierz wzorcowy; ; kl. 0,2; nr PL-P3-642/E6; zakres 60 mV;

mV_x - miliwoltomierz badany; ; kl. 0,5; nr PL-P3-233-E6; zakres 60 mV.

w[dz]	w[dz]	αx [dz]		x[dz]	α [dz]	α [dz]	Uw [mV]		Ux [mV]
rosnąco	malejąco	rosnąco	malejąco	rosnąco	malejąco	rosnąco	malejąco	rosnąco	malejąco
19	124	10	60	0,5	-2	7,6	49,6	8	48
41	103	20	50	-0,5	-1,5	16,4	41,2	16	40
62	82	30	40	-1	-1	24,8	32,8	24	32
82	62	40	30	-1	-1	32,8	24,8	32	24
103	41	50	20	-1,5	-0,5	41,2	16,4	40	16
124	20	60	10	-2	0	49,6	8	48	8

Przykłady obliczeń:

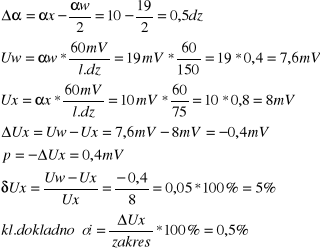
Wyznaczenie płynności regulacji:

Sprawdzenie płynności regulacji polega na zmianie rezystancji o taką wartość, aby napięcie zmieniło się o wartość minimalną α=1dz . Dla początku skali zmiana rezystancji przy zmianie napięcia o 1dz jest bardzo duża

a) dla małego napięcia zasilającego

początek skali: zmiana rezystancji przy zmianę napięcia o 1 dz. jest bardzo duża;

koniec skali: 75 dz. -35,1Ω;

74 dz. - 35,7 Ω;

błąd dopuszczalny wynikający z klasy użytego przyrządu wynosi:

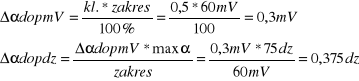
p =

b) dla dużego napięcia zasilającego

początek skali: zmiana rezystancji przy zmianie napięcia o 1 dz. jest bardzo duża;

koniec skali: 75 dz. - 250,2 Ω; ΔR_d = 0,1 Ω

74 dz. - 253,8 Ω;

płynność =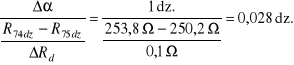

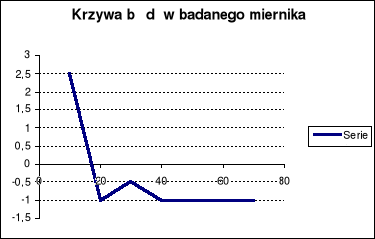
Na podstawie otrzymanych pomiarów przy wzrastającym i malejącym odchyleniu wykreśliłem charakterystykę

Na wykresie Δα=f(α) przedstawione zostały błędy dla ocyfrowanych podziałek miernika dla zakresu 60mV otrzymane przy wzrastającym i malejącym odchyleniu. Osie wyskalowane są w działkach(dz).

W tym przypadku obydwa wykresy pokrywają się.

2. Sprawdzenie badanego miliwoltomierza jako miliamperomierza na zkresie30mA przez dołączenie bocznika.

Schemat pomiarowy:

Przyrządy użyte do pomiaru:

Z - zasilacz napięcia stałego KB−6118

R_d - opornik dekadowy; nr PL-P3-305-E6;

mA_w - miliamperomierz wzorcowy; ; kl. 0,2; nr PL-P3-642-E6; zakres 30 mA;

mA_x - miliamperomierz badany; ; kl. 0,5; nr PL-P3-233-E6; zakres 30 mA.

αw	αx			p		Kl. dokł	Iw	Ix
[dz]	[dz]	[dz]	[mA]	[mA]	[%]	[%]	[mA]	[mA]
74	73	-1	0,4	-0,4	1,37	0,53	29,6	29,2

Przykłady obliczeń:

73dz-74dz=-1dz

29,6mA-29,2mA=0,4mA

p=-

3. Wyznaczanie rezystancji opornika dodatkowego, potrzebnego do poszerzenia zakresu z 3V do 15V

Schemat pomiarowy:

Użyte przyrządy:

Zasilacz stabilizowany KB-6118 PL-T-4147-EZ-M

Rezystor dekadowy DR6-16 PL-P3-305-E6

Woltomierz wzorcowy kl. 0,2 PL-P3-652/E6, 150dz-15V

Woltomierz badany kl. 0,5 PL-P3-233-E6, 75dz-3V

Wartość rezystancji ustawiona na rezystorze dekadowym wynosi:

Rd=Rp∗(m-1) , gdzie m- mnożnik zakresu m=
Rp=1500Ω

Rd=1500∗(5-1)=6000Ω

		Δα [dz]	Uw[V]	Ux[V]
15	10	2,5	1,5	0,4
42	20	-1	4,2	0,8
61	30	-0,5	6,1	1,2
82	40	-1	8,2	1,6
102	50	-1	10,2	2
122	60	-1	12,2	2,4
142	70	-1	14,2	2,8

Przykłady obliczeń:

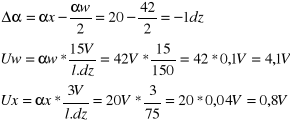
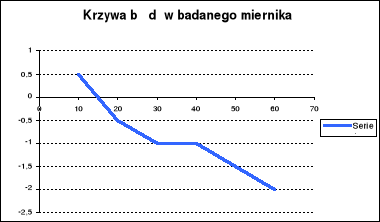
Na podstawie otrzymanych pomiarów wykreśliłem krzywą błędów;

Wnioski:

Na wykresie Δα = f(α) przedstawiono błędy dla ocyfrowanych podziałek miernika dla zakresu 60mV, dla końcowego punktu podziałki miernika dla zakresu 30mA oraz wykreślne wyznaczenie błędów dla pozostałych ocyfrowanych punktów podziałki miernika dla zakresu 30mA.

Drugi wykres Δα_3V = f(α) przedstawia błędy miernika dla zakresu 3V poszerzonego do 15V. Wykres ten różni się od wykresu Δα = f(α) ze względu na zastosowanie opornika dodatkowego. Opornik ten zmniejszył, i to znacznie, błąd miernika, co można uznać za pewnego rodzaju kompensację.

mV_w

R_d

Z

R

mV_x

W

~

~

mA_w

mA_x

R_d

Z

W

R

R_d

Z

V_x

W

~

V_w

---