DZIEDZINA ZMIENNEJ CZASU t (zmiennej rzeczywistej t)			DZIEDZINA ZMIENNEJ OPERATOROWEJ s (zmiennej zespolonej s=a+jb)
Model matematyczny obiektu:
		Przekształcenie Laplace'a L[ f(t) ] = F(s) Oryginał Transformata		Równanie z niewiadomą Y(s) np.:
Rachunek różniczkowy, całkowy				Rozwiązujemy względem Y(s)
Rozwiązanie: y(t)=... np.:				Otrzymujemy funkcję wymierną (iloraz dwóch wielomianów) np.:
				Rozkładamy na ułamki proste
				np.:
		Odwrotne przekształcenie Laplace'a y(t) = L^-1[ Y(s) ] Oryginał Transformata

PRZEKSZTAŁCENIE LAPLACE`A

Przekształcenie Laplace'a przyporządkowuje funkcji zmiennej rzeczywistej f(t) funkcje F(s) zmiennej zespolonej, s według wzoru zwanego całką Laplace'a

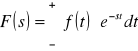
Funkcja f(t) nazywa się oryginałem, a odpowiadająca jej funkcja F(s) - transformatą.

Własności przekształcenia Laplace`a:

1. Twierdzenie o liniowości:

,

.

Powyższe dwa twierdzenia zapisać można w postaci wzoru ogólnego

2. Twierdzenie o transformacji pochodnych:

,

.

3. Twierdzenie o przesunięciu w dziedzinie zmiennej rzeczywistej:

.

4. Twierdzenie o przesunięciu w dziedzinie zmiennej zespolonej:

Jeżeli

to
.

5. Twierdzenie o zmianie skali:

Jeżeli
i
,

to
.

6. Twierdzenie o różniczkowaniu w dziedzinie zmiennej zespolonej:

Jeżeli
,

to

oraz
.

7. Twierdzenie o transformacie funkcji okresowej

Jeżeli dana jest funkcja okresowa

gdzie k=1, 2, 3,...

oraz transformata funkcji f(t) za jeden okres

,

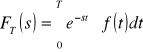
to

.

8. Twierdzenie o wartości końcowej

Jeżeli istnieje

i
,

to

.

9. Twierdzenie o wartości początkowej

Jeżeli istnieje

i
,

to

.

10. Twierdzenie o splocie

,

gdzie
jest splotem funkcji
i
.

Splot funkcji określa zależność

.

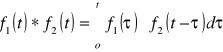
TRANSFORMATY LAPLACE`A NAJCZĘŚCIEJ SPOTYKANYCH FUNKJI

Lp.	Oryginał	Transformata
1	impuls jednostkowy (funkcja Diraca)	1
2	skok jednostkowy funkcja Heviside`a)
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

ODWROTNE PRZEKSZTAŁCENIE LAPLACE`A

Odwrotne przekształcenie Laplace'a przyporządkowuje funkcji F(s) zmiennej zespolonej s funkcje, f(t) zmiennej rzeczywistej t według wzoru zwanego całką Riemanna-Mellina. Przyporządkowanie to przyjęto zapisywać za pomocą symbolu:

.

Ponieważ obliczanie całki Riemanna-Mellina jest pracochłonne, przy wyznaczaniu oryginału danej funkcji zmiennej zespolonej wykorzystuje się, o ile to możliwe, wyżej podane własności przekształcenia Laplace'a oraz tabelę transformat.

Najczęściej transformata ma postać ilorazu wielomianów, który można sprowadzić do postaci:

,

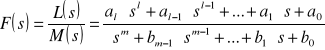
przy czym
.

W celu znalezienia oryginału tego rodzaju transformaty należy ją rozłożyć na sumę ułamków prostych i oryginały poszczególnych ułamków wyznaczyć za pomocą tablic przekształceń Laplace`a.

Jeżeli wielomian
mianownika transformaty
nie posiada wielokrotnych miejsc zerowych, to rozkład na ułamki proste przeprowadza się według wzoru

,

w którym:
, ...,
- miejsca zerowe wielomianu
,

, ...,
- stałe współczynniki.

Współczynniki
, ...,
wyznaczyć można ze wzoru

,

w którym oznaczono

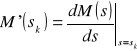
lub ze wzoru

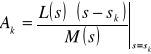
Podane wzory obowiązują również w przypadku, w którym jedno z miejsc zerowych wielomianu
jest zerem.

Jeżeli wielomian mianownika
posiada oprócz pojedynczych miejsc zerowych również wielokrotne, np. p-krotne n-te miejsce zerowe, to rozkład na ułamki proste przeprowadza się według wzoru

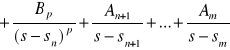
Współczynniki
, ...,
wyznacza się ze wzorów powyżej podanych, natomiast współczynniki
, ...,
ze wzorów

,

,

,

.

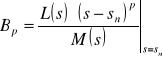
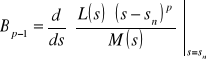
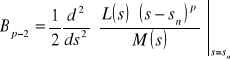
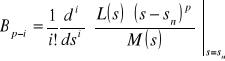
ROZWIĄZYWANIE LINIOWYCH RÓWNAŃ RÓŻNICZKOWYCH ZWYCZAJNYCH ZA POMOCĄ PRZEKSZTAŁCENIA LAPLACE'A

Doniosła rola przekształcenia Laplace'a polega między innymi na tym, że daje ono prostą metodę rozwiązywania równań różniczkowych, polegającą na ich algebraizacji.

Niech dane będzie zwyczajne równanie różniczkowe ze stałymi współczynnikami

,

w którym
jest znaną funkcją zmiennej rzeczywistej, oraz warunki początkowe.

Rozwiązując równanie należy:

1. poddać je przekształceniu Laplace'a z uwzględnieniem warunków początkowych,

2. wyznaczyć transformatę
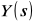
   szukanej funkcji,

3. doprowadzić tę transformatę do postaci

,

4. wyznaczyć szukaną funkcję zmiennej rzeczywistej

.

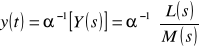
ZADANIA

Zadanie 1.

Wyznaczyć transformatę funkcji jednostkowej
, przyjmując, że:

.

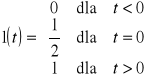
Rozwiązanie:

.

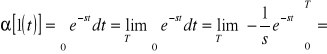
Powyższa granica jest określona dla takich s, których część rzeczywista jest większa od zera. A więc jeśli:

,

to
,

stąd
.

Zadanie 2.

Wyznaczyć transformatę funkcji
, przedstawionej na rysunku:

Rozwiązanie:

.

Całka jest określona dla wartości s, spełniających warunek
, a więc

.

Rozwiązanie wynika również bezpośrednio z twierdzenia

o przesunięciu w dziedzinie zmiennej rzeczywistej.

Zadanie 3.

Wyznaczyć oryginał funkcji:

.

Rozwiązanie:

Transformatę należy rozłożyć na sumę ułamków prostych:

.

Miejscami zerowymi mianownika są:

,
,
.

Współczynniki
,
,
można obliczyć według wzoru

,

,
,
,

.

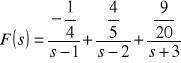
Na podstawie tablic przekształceń Laplace'a mamy:

Lp.	Oryginał	Transformata
5

a więc:

.

PRACA DOMOWA

Zadanie 4.

Wyznaczyć oryginał funkcji:

.

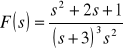
Rozwiązanie:

Mianownik posiada potrójne miejsce zerowe
oraz podwójne
. Rozkład na czynniki należy przeprowadzić według wzoru:

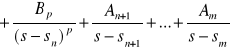
czyli:

.

Współczynniki
,
,
,
,
należy wyznaczyć według wzorów:

,

,

,

.

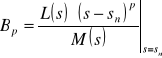
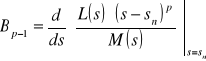
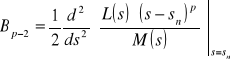
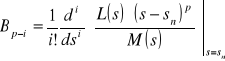
czyli:

,

,

,

,

.

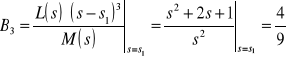
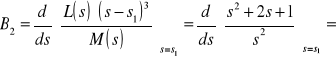
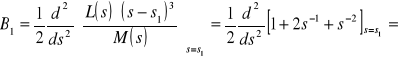
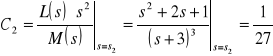
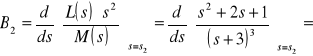
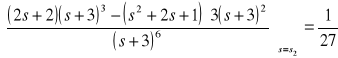
Oryginały poszczególnych ułamków wyznaczamy na podstawie tablic przekształceń Laplace'a.

.

	1
		Ćwiczenia dr inż. Krzysztof Przystupa

---