Wykład 15

Elektrostatyka

Obecnie wiadome są cztery fundamentalne oddziaływania: silne, elektromagnetyczne, słabe i grawitacyjne. Silne i słabe oddziaływania odgrywają decydującą role w budowie jąder atomowych i cząstek elementarnych. Oddziaływanie grawitacyjne jest odpowiedzialne za budowę galaktyk, układów planetarnych czyli układów ciał o dużych masach. Oddziaływanie elektromagnetyczne jest jednym z najważniejszych w fizyce i pozwala wyjaśnić nie tylko zjawiska elektryczne i magnetyczne ale też siły zespalające materię na poziomie atomów, cząsteczek.

Poznawanie zjawisk elektromagnetycznych zaczniemy od elektrostatyki. Elektrostatyka zajmuje się badaniem właściwości i wzajemnego oddziaływania nieruchomych ładunków.

Fundamentalne właściwości ładunków

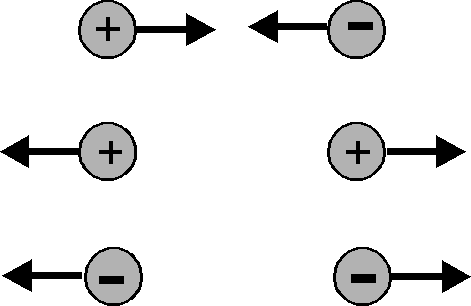
Elektryczne oddziaływania zachodzą między cząstkami, które posiadają tak zwany ładunek elektryczny. Z doświadczeń wynika, że ładunki mogą być dwóch różnych znaków. Ładunki dodatnie powstają np. na szkle potartym kawałkiem skóry, natomiast ładunki ujemne powstają na bursztynie potartym kawałkiem wełny. W odróżnieniu od siły oddziaływania grawitacyjnego, która zawsze jest siłą przyciągania, elektrostatyczna siła oddziaływania dwóch ładunków może być lub siłą przyciągania lub siłą odpychania: ciała niosące ładunki jednoimienne odpychają się natomiast ciała niosące ładunki różnoimienne przyciągają się.

Ładunki jednoimienne odpychają się a ładunki różnoimienne przyciągają się

Z doświadczeń wynikają trzy fundamentalne właściwości ładunku elektrycznego: 1. Ładunek elektryczny może przybierać jedynie wartości będące - co do modułu -wielokrotnością ładunku elektronu: , (XV.1) gdzie jest ujemną lub dodatnią liczbą całkowitą, a jest ładunkiem elektronu.

W układzie SI jednostką ładunku jest kulomb (
). Wartość ładunku elektronu w układzie SI wynosi

.

Właściwość (XV.1), czyli dyskretność ładunku elektrycznego nosi nazwę kwantyzacji ładunku. Mówimy, że ładunek elektryczny jest wielkością skwantowaną.

2. Całkowity ładunek elektryczny układu odosobnionego, tzn. suma algebraiczna ładunków ujemnych i dodatnich układu, jest wielkością inwariantną (niezmienniczą). Właściwość ta nazywa się prawem zachowania ładunku elektrycznego.

3. Wartość ładunku elektrycznego nie zależy od tego czy ładunek jest ruchomy, czy nieruchomy. Mówimy więc, że ładunek elektryczny jest wielkością relatywistycznie niezmienniczą.

Pole elektryczne. Natężenie i linii pola elektrycznego. Prawo Coulomba.

Jedynym sposobem wykrycia i zmierzenia ładunków elektrycznych jest badanie oddziaływania zachodzącego między ciałami naładowanymi. Istnienie w przestrzeni pola elektromagnetycznego możemy wykryć obserwując zachowanie małego (punktowego) ładunku elektrycznego - ładunku próbnego. Z doświadczeń wynika, że jeżeli w przestrzeni istnieje pole elektryczne, to na mały próbny ładunek
działa siła wprost proporcjonalna do

. (XV.2)

Wektor
jest funkcją współrzędnych
punktu w którym znajduje się ładunek próbny
i nie zależy od
. Dla drugiego małego próbnego ładunku
, umieszczonego w tym samym punkcie o współrzędnych
na ładunek
będzie działała siła

. (XV.3)

Zgodnie z drugą zasadą Newtona pod wpływem siły (XV.2) próbny ładunek będzie poruszać się z przyspieszeniem, a zatem z obserwacji tego, że ładunek próbny umieszczony w przestrzeni zaczyna poruszać się z przyspieszeniem wprost proporcjonalnym do
, wnioskujemy, że w przestrzeni istnieje pole elektryczne. Pole elektryczne działające na nieruchomy ładunek będziemy nazywały polem elektrostatycznym.

Ze wzoru (XV.2) widać, że pole elektrostatyczne albo prosto pole elektryczne w każdym punkcie przestrzeni jest określone przez wektor
. Wektor
nazywa się wektorem natężenia pola elektrycznego i zgodnie z (XV.2) natężenie pola elektrycznego jest równe sile działającej na ładunek próbny q (umieszczony w danym punkcie przestrzeni) podzieloną przez ten ładunek.

. (XV.4)

Jeżeli ładunek
jest dodatni, to kierunek
jest taki sam jak
.

W 1785 roku Coulomb^♣) udowodnił doświadczalnie, że siła z której ładunek
działa na ładunek
wynosi

, (XV.5)

gdzie
jest odległość między ładunkami
i
;
jest jednostkowym wektorem skierowanym od pierwszego ładunku ku drugiemu ładunkowi. Stała
we wzorze (XV.5) zależy wyłącznie od stosowanego układu jednostek. W układzie SI

=

. (XV.6)

W tym wzorze współczynnik
= 8.854·10^-12
nosi nazwę przenikalności elektrycznej próżni.

Pisząc równanie (XV.5) zakładamy, że ładunki są punktami materialnymi. Podkreślimy również, że rozważając ładunki nieruchome pomijamy istnienie sił magnetycznych. Siły magnetyczne między ładunkami powstają przy ruchu ładunków i będą omawiane dalej.

Ze wzoru (XV.5) wynika, że siła z której ładunek
działa na ładunek
wynosi

, (XV.7)

Tu
jest jednostkowym wektorem skierowanym od drugiego ładunku ku pierwszemu ładunkowi. Jak i powinno być, wzór (XV.7) po prostu wyraża trzecią zasadę Newtona.

Umieścimy ładunek
w początku układu odniesienia. Wtedy oznaczając
i biorąc pod uwagę, że w kierunku dowolnego wektora
jednostkowy wektor jest równy:

^♣^) Charles-Augustin de Coulomb (1736-1806), a military civil engineer, retired from the French army because of ill health after years in the West Indies. Forced from Paris by the disturbances of the revolution, he began working at his family estate and discovered that the torsion characteristics of long fibers made them ideal for the sensitive measurement of magnetic and electric forces. He was familiar with Newton's inverse-square law and in the period 1785-1791 he succeeded in showing that electrostatic forces obey the same rule.

,

wzór (XV.5) możemy zapisać w postaci

, (XV.8)

Ze wzoru (XV.8) widzimy, że ładunek
jest źródłem pola elektrycznego o natężeniu

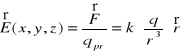
. (XV.9)

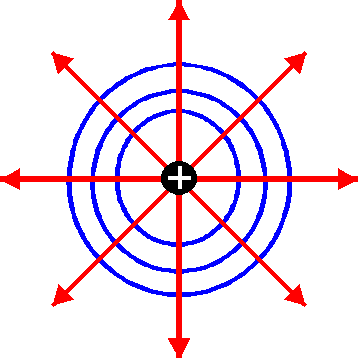
Poglądowym sposobom graficznego przedstawienia pola elektrycznego jest rysowanie linii natężenia pola. Linii natężenia pola elektrycznego rysujemy w następujący sposób: 1) styczna do linii pola w dowolnym punkcie określa zwrot natężenia pola , który pokrywa się ze strzałką linii pola; 2) linie pola wykreśla się tak, aby liczba linii na jednostkę powierzchni przekroju była proporcjonalna do wielkości
. Linii natężenia pola elektrycznego wytworzonego przez dodatni ładunek są przedstawione na rysunku niżej.

Linii natężenia pola elektrycznego ładunku naładowanego dodatnie.

Zasada superpozycji

Z doświadczeń wynika, że siła działająca na próbny ładunek
, umieszczony w dowolnym punkcie (
) układu ładunków
jest wektorową sumą sił przyłożonych do niego ze strony każdego z ładunków
:

, (XV.10)

gdzie
jest wektorem łączącym
-ty ładunek układu z punktem (
).

Wzór (XV.10) wyraża ważną w elektrostatyce zasadę superpozycji sił. Ze wzoru (XV.10) wynika, że natężenie pola elektrycznego wytwarzanego w dowolnym punkcie (
) ładunkami
jest równe

, (XV.11)

Jeżeli rozkład ładunku jest ciągły, pole wytworzone przez ciało naładowane możemy obliczyć dzieląc ciało na nieskończenie małe kawałki o ładunku
. Traktując każdy taki ładunek jako ładunek punktowy obliczamy wytworzone przez niego pole

, (XV.12)

gdzie
jest odległością ładunku
od punktu (
). Wypadkowe pole w punkcie (
) znajdujemy całkując wkłady od wszystkich elementów ciała naładowanego

. (XV.13)

Przy wyliczeniu całki we wzorze (XV.13), w zależności od geometrii naładowanego ciała, wprowadzamy pojęcie gęstości ładunku.

Przy ciągłym rozkładzie ładunków wzdłuż linii mówimy o gęstości liniowej ładunków elektrycznych
, równej

, (XV.14)

gdzie
oznacza całkowity ładunek rozłożony wzdłuż odcinka linii o długości
.

Jeżeli rozważamy naładowany kawałek powierzchni, to posługujemy się pojęciem gęstości powierzchniowej ładunków
, równej

, (XV.15)

gdzie
jest całkowitym ładunkiem elementu powierzchni
.

W przypadku ciągłego rozkładu ładunków w pewnej objętości wprowadzamy gęstość objętościową ładunków
, która jest równa

, (XV.16)

gdzie
oznacza całkowity ładunek elementu objętości
.

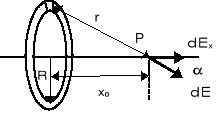
Jako przykład obliczenia pola elektrycznego w przypadku ciągłego rozkładu ładunku rozważmy pole naładowanego pierścienia o promieniu
całkowity ładunek którego wynosi
. Znajdziemy pole elektryczne na osi pierścienia w odległości
od środka.

Składowa pola wzdłuż osi wytwarzane przez element pierścienia jest równe . Wprowadzając liniową gęstością ładunku ze wzoru (XV.12) mamy .

A więc

.

Stąd

.

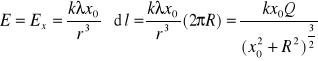
Zwróćmy uwagę, że w środku pierścienia (x₀ = 0) E = 0, a dla x₀ >> R pole
i jest takie samo jak pole ładunku punktowego w tej odległości.

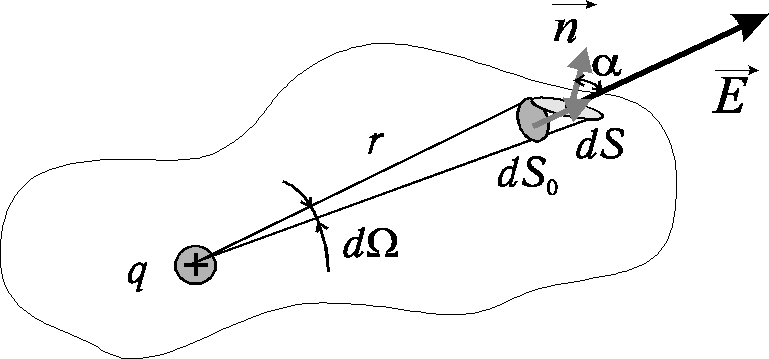
Strumień pola elektrycznego

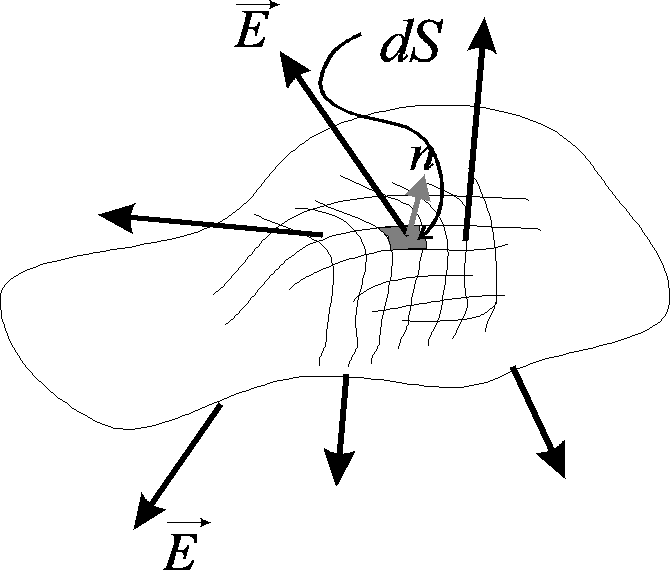
Rozważmy zamkniętą powierzchnie, coś w rodzaju balonu o dowolnym kształcie, w przestrzeni gdy istnieje pole elektryczne. Podzielmy całą powierzchnie na tak małe kawałki
, że na każdym z tych kawałków powierzchnię możemy uważać za płaską, a wektor natężenie pola elektrycznego
jest prawie stałe. Przedstawmy pole takiej małej elementarnej powierzchni wektorem
, gdzie
jest jednostkowym wektorem normalnym do powierzchni
i skierowanym na zewnątrz. Iloczyn skalarny
nazywamy strumieniem pola elektrycznego
przez element powierzchni
:

. Strumień pola elektrycznego przez całą powierzchnie otrzymujemy sumując strumieni przez wszystkie elementy powierzchni . (XV.17)

Zmniejszając rozmiary i zwiększając liczbę elementów
przechodzimy w granice w równaniu (XV.17) do całki powierzchniowej

. (XV.18)

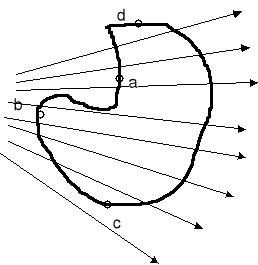
Jako przykład obliczmy strumień pola elektrycznego ładunku punktowego
przez dowolną powierzchnie zamkniętą
, obejmującą ten ładunek.

Strumień pola elektrycznego przez element tej powierzchni wynosi . Wielkość jest polem rzutu elementu na płaszczyznę prostopadłą do wektora .

Z dokładnością do nieskończenie małych wielkości można uważać, że
równa się polu powierzchni
, którą wyznacza stożek na powierzchni kuli o promieniu
. A zatem

. (XV.19)

W matematyce stosunek pola powierzchni
, wyznaczonego na powierzchni kuli o promieniu
przez stożek do kwadratu promienia kuli

(XV.20)

nazywa się kątem bryłowym. Kąt bryłowy określa powierzchnie
na powierzchni wewnętrznej sfery, wyświetlanej latarką znajdującej się w początku sfery. Kąt bryłowy mierzymy w steradianach. Jednemu steradianowi odpowiada pole powierzchni
. Ponieważ całkowite pole powierzchni kuli wynosi
, przeto pełny kąt bryłowy odpowiadający całej powierzchni kuli wynosi
steradianów.

Podstawiając (XV.20) do wzoru (XV.19) otrzymujemy

. (XV.21)

Całkując to wyrażenie względem całej powierzchni
, tj. względem
od 0 do
znajdujemy

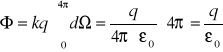
. (XV.22)

Otrzymaliśmy ważny wynik: strumień pola elektrycznego ładunku punktowego
przez dowolną powierzchnie zamkniętą
, obejmującą ten ładunek nie zależy od kształtu powierzchni. Ze wzoru (XV.22) wynika, że całkowita liczba linii pola elektrycznego wychodzących (albo wchodzących) od ładunku jest równa
i linie te ciągną się do nieskończoności.

Prawo Gaussa

Niech zamknięta powierzchnia obejmuje dwa ładunki
i
. Korzystając z zasady superpozycji dla całkowitej liczby linii pola przecinającej powierzchnię zamkniętą wokół ładunków
i
możemy zapisać

. (XV.23)

Otrzymaliśmy, że całkowita liczba linii pola jest równa całkowitemu ładunkowi podzielonemu przez
. Podobnie można pokazać , że dla dowolnej liczby
ładunków

, (XV.24)

gdzie
jest całkowitym ładunkiem.

Wzór (XV.24) wyraża prawo Gaussa: strumień pola wychodzący z naładowanego ciała jest równy wypadkowemu ładunkowi podzielonemu przez
. Jeżeli
jest ujemne strumień wpływa do ciała.

W sytuacji gdy na zewnątrz zamkniętej powierzchni są ładunki wypadkowy wewnętrzny ładunek , a zatem ilość linii pola wchodząca do zamkniętej powierzchni równa się ilości linii wychodzących. Rozpatrzmy kilku przykładów obliczania pola elektrycznego na podstawie prawa Gaussa.

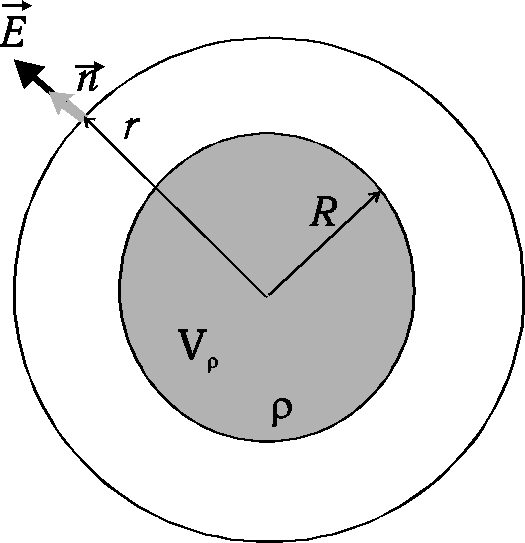
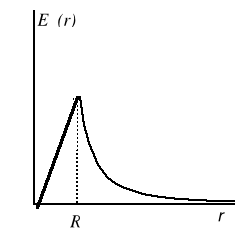
1. Pole elektryczne jednorodnie naładowanej kuli o promieniu
.

Zgodnie z kulistą symetrią zadania w dowolnym punkcie sfery o promieniu wektor natężenia pola elektrycznego ma taką samą wartość, a kierunek pokrywa się z kierunkiem wektora . Wtedy korzystając z prawa Gaussa dla pola wewnątrz kuli na sferze o promieniu możemy zapisać:
	, gdzie . A zatem . (XV.25)

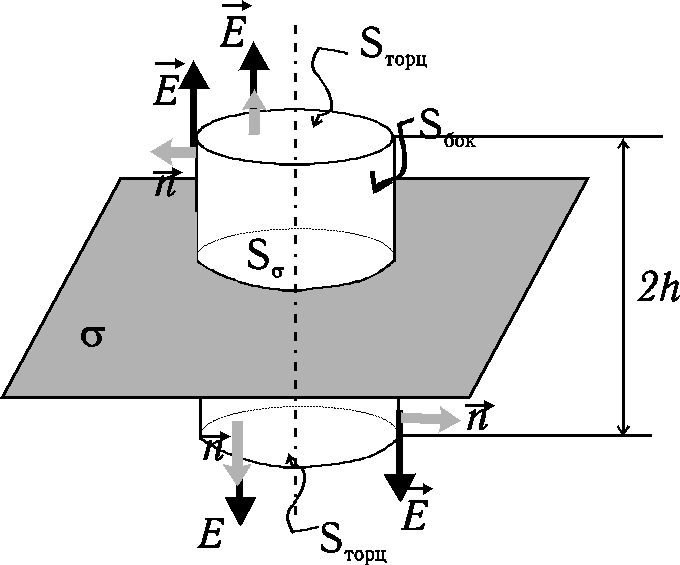
2. Pole elektryczne od nieskończonej jednorodnie naładowanej płaszczyzny.

Ładunek otoczony przez powierzchnię walca jest równy , gdzie jest gęstością powierzchniową ładunku, a - powierzchnią podstawy walca. Korzystając z prawa Gaussa otrzymujemy , gdzie czynnik 2 odpowiada dwóm podstawom walca.

Ostatecznie otrzymujemy

. (XV.26)

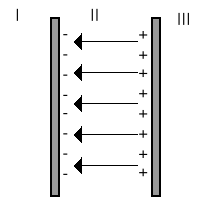
3. Pole elektryczne wewnątrz kondensatora płaskiego.

Płaski kondensator składa się z dwóch równoległych płyt. Pole wytwarzane przez płytę "po lewej stronie" (rysunek) jest równe i skierowane ku płycie. Pole wytwarzane przez płytę po prawej stronie jest równe i skierowane jest od płyty.

Zatem w obszarze I

,

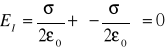
w obszarze II

,

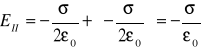
w obszarze III

.

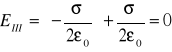
12

---