1

Wykład 15.

Elektryczność i magnetyzm. Równania Maxwella

Ciekawe strony internetowe:

http://en.wikipedia.org/wiki/

(* wikipedia *)

http://hyperphysics.phy-astr.gsu.edu/

http://www.falstad.com/mathphysics.html

(* komputerowe demonstracje fizyczne*)

1.

Prawo indukcji Faradaya

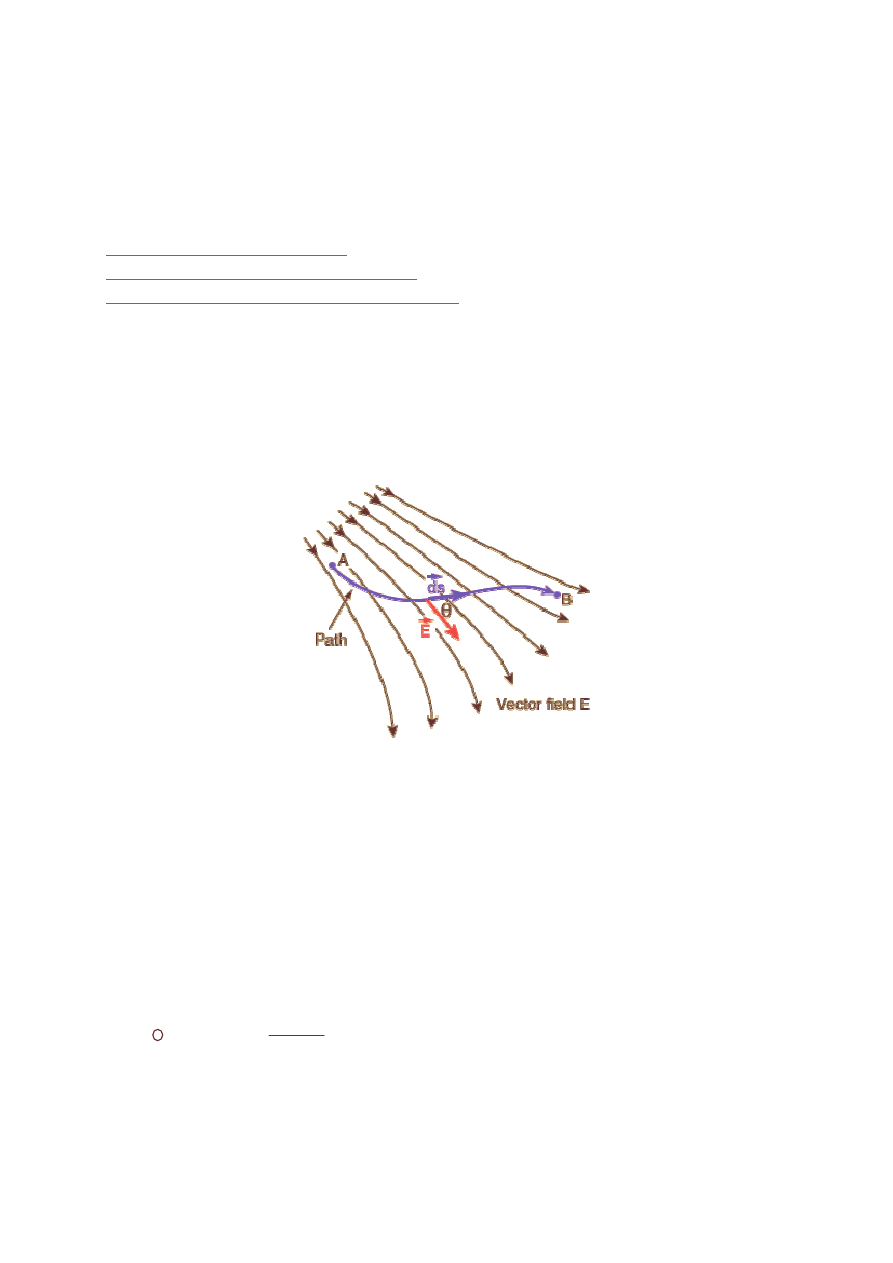
Cyrkulacja, krążenie pola elektrycznego definiujemy w sposób następujący
(patrz rysunek)

Rys 1.1 Cyrkulacja pola elektrycznego

dl

l

d

E

E

l

d

E

B

A

B

A

∫

∫

=

)

,

cos(

r

r

r

r

(1.1.1)

Prawo Faradaya mówi, że cyrkulacja pola elektrycznego wywołana jest zmianą
pola magnetycznego.

dt

d

l

d

E

B

Φ

−

=

∫

r

r

(1.1.2)

Po podstawieniu definicji strumienia pola magnetycznego otrzymamy
następującą postać prawa Faraday’a:

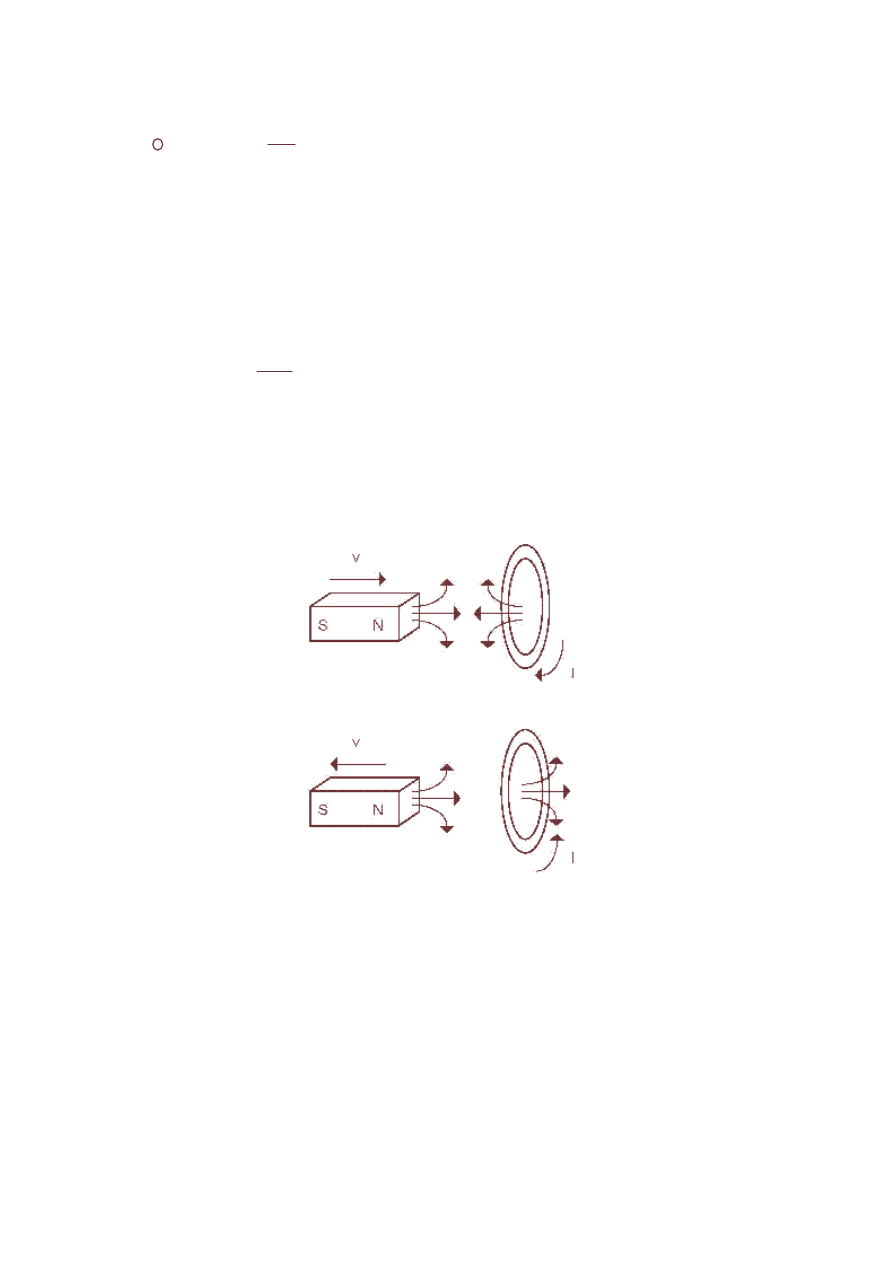
2

∫

∫

−

=

A

C

A

d

B

dt

d

l

d

E

r

r

r

r

(1.1.3)

gdzie kontur C obejmuje powierzchnię A.

Jest to postać całkowa prawa Faraday’a. Postać różniczkowa wygląda
następująco:

t

B

E

rot

∂

∂

−

=

r

r

(1.1.4)

Prawo Faradaya mówi, że zmiana pola magnetycznego powoduje powstanie
pola elektrycznego. Znak minus występujący w równaniach 1.1.3 i 1.1.4 jest to
reguła Lentza. Pole elektryczne wzbudzane jest w takim kierunku, aby
przeciwdziałać zmianie pola magnetycznego, która go wywołała.

Rys. 1.1 Reguła Lentza.

1.1

Indukcja własna

Weźmy cewkę indukcyjną N zwojach. Jeżeli prąd przepływający przez
uzwojenie zmienia się, to zgodnie z prawe Faradaya zmienia się strumień pola
magnetycznego, czyli w uzwojeniu cewki indukuje się siła elektromotoryczna
indukcji SEM równa:

3

dt

d

N

B

SEM

Φ

−

=

ε

(1.1.5)

Ostatecznie otrzymujemy wzór:

dt

dI

L

SEM

−

=

ε

(1.1.6)

gdzie I – natężenie prądu płynącego w uzwojeniu cewki, L – współczynnik
indukcji, indukcyjność zwojnicy.

1.2

Indukcja wzajemna

Gdy mamy cewki, zmiana prądu w jednej może powodować indukowanie siły
elektromotorycznej SEM w drugiej cewce. Strumień przechodzący przez drugą
cewkę jest proporcjonalny do zmian prądu w pierwszej cewce (i na odwrót).

dt

dI

M

2

12

1

−

=

ε

(1.1.7a)

dt

dI

M

1

21

2

−

=

ε

(1.1.7b)

gdzie M

12

, M

21

– współczynniki indukcji wzajemnej.

W idealnych warunkach, gdy cały strumień pola wytwarzany przez pierwszą
zwojnicę przenika przez uzwojenie drugiej zwojnicy wtenczas współczynnik
M

12

jest równy:

2

1

12

L

L

M

=

(1.1.8a)

W rzewistości zawsze mamy straty, stąd

2

1

12

L

L

M

<

(1.1.8b)

4

Prawo Faradayą jest niezwykle ważne ze względu na swoje reperkusje. Można
powiedzieć, że przemył energetyczny, elektromaszynowy oparty jest na
zastosowaniach prawa Faradaya w takich dziedzinach jak: silniki elektryczne,
generatory prądu, transformatory i wiele innych.

2.

Równania Maxwella

James Clerk Maxwell (1831 – 1879)

Równania Maxwella: zbiór czterech równań, zebranych przez J. C. Maxwella,
opisujących zachowanie pola elektrycznego i magnetycznego oraz ich
oddziaływanie z materią.

5

Tabela 1. Równania Maxwella.

forma różniczkowa

forma całkowa

I

prawo Gaussa
(dla pola
elektrycznego)

ρ

=

D

div

r

Q

A

d

D

A

=

∫

r

r

II

prawo Gaussa
(dla pola
magnetycznego)

0

=

B

div

r

0

=

∫

A

A

d

B

r

r

III

prawo Fradaya

t

B

E

rot

∂

∂

−

=

r

r

A

d

B

t

d

d

l

d

E

A

l

r

r

r

r

∫

∫

−

=

IV

prawo Ampera
(uzupełnione
przez Maxwella)

t

D

j

H

rot

∂

∂

+

=

r

r

r

A

d

t

D

A

d

j

l

d

H

A

A

l

r

r

r

r

r

r

∫

∫

∫

∂

∂

+

=

Pierwsze równanie Maxwella: pole elektryczne jest polem źródłowym, istnieją
ładunki elektryczne.

Drugie równanie Maxwella: pole magnetyczne jest polem bezźródłowym, nie
istnieją monopole magnetyczne.

Trzecie równanie Maxwella to prawo Faradaya o indukcji. Zmienne pole
magnetyczne powoduje powstanie pola elektrycznego.

Czwarte równanie Maxwella to prawo Ampera z dodanym członem
odpowiedzialnym za tzw. prąd przesunięcia. Prądy i zmienne pole elektryczne
powodują powstanie pola magnetycznego.

Znaczenie wielkości występujących w równaniach Maxwella:

Tabela 2. Oznaczenia użyte w równaniach Maxwella.

Oznaczenie

Nazwa

Powiązania

E

r

natężenie pola elektrycznego

D

r

indukcja pola elektrycznego

E

D

r

r

ε

ε

0

=

H

r

natężenie pola magnetycznego

B

r

indukcja pola magnetycznego

H

B

r

r

µ

µ

0

=

j

r

gęstość prądu

ρ

gęstość ładunku

6

A

d

r

różniczkowy element powierzchni,
normalny do tej powierzchni

l

d

r

różniczkowy element krzywej L
zawierającej powierzchnię A

⋅

∇

lub

div

operator dywergencji (źródłowości)

×

∇

lub

rot

operator rotacji (cyrkulacji, krążenia)

0

0

,

ε

µ

przenikalność magnetyczna, elektryczna,
próżni

0

0

1

µ

ε

=

c

ε

µ

,

względna przenikalność magnetyczna,
elektryczna, materiału

Konsekwencje równań Maxwella.

2.1

Zasada zachowania ładunku

Z równań Maxwella można otrzymać związek między natężeniem prądu a
zmianą ładunku. Opisuje to równanie:

t

j

div

∂

∂

−

=

ρ

r

(1.2.3)

Całkowity prąd wypływające przez dowolną powierzchnię zamkniętą jest równy
zmianie ładunku (ze znakiem minus) wewnątrz tej powierzchni.
Jest to treść zasady zachowania ładunku.

2.2

Pole elektromagnetyczne w próżni

W próżni, w nieobecności ładunków i prądów, równania Maxwella przybiorą
postać:

0

=

D

div

r

0

=

B

div

r

t

B

E

rot

∂

∂

−

=

r

r

(2.2.1)

7

t

D

H

rot

∂

∂

=

r

r

gdzie związek między natężeniem a indukcją pola jest następujący:

E

D

r

r

0

ε

=

H

B

r

r

0

µ

=

(2.2.2)

Układ równań różniczkowych (2.2.1) sprowadza się do równania fali, które dla
przypadku fali jednowymiarowej przybiera postać:

2

2

2

2

2

1

t

E

c

x

E

∂

∂

=

∂

∂

(2.2.3)

przykład równania dla pola elektrycznego. Analogiczne równanie dla pola
magnetycznego.

Rozwiązaniem równania 2.2.3 jest zmienne pole elektryczne i magnetyczne o
równaniu, odpowiednio:

)

sin(

0

kx

t

E

E

−

=

ω

)

sin(

0

kx

t

B

B

−

=

ω

(2.2.4)

oczywiście dotyczy to przypadku fali jednowymiarowej.

Zgodnie z równaniami Maxwella iloraz amplitud pola amgnetyczngo i
elektrycznego jest związana zależnością:

c

B

E

=

0

0

(2.2.5)

8

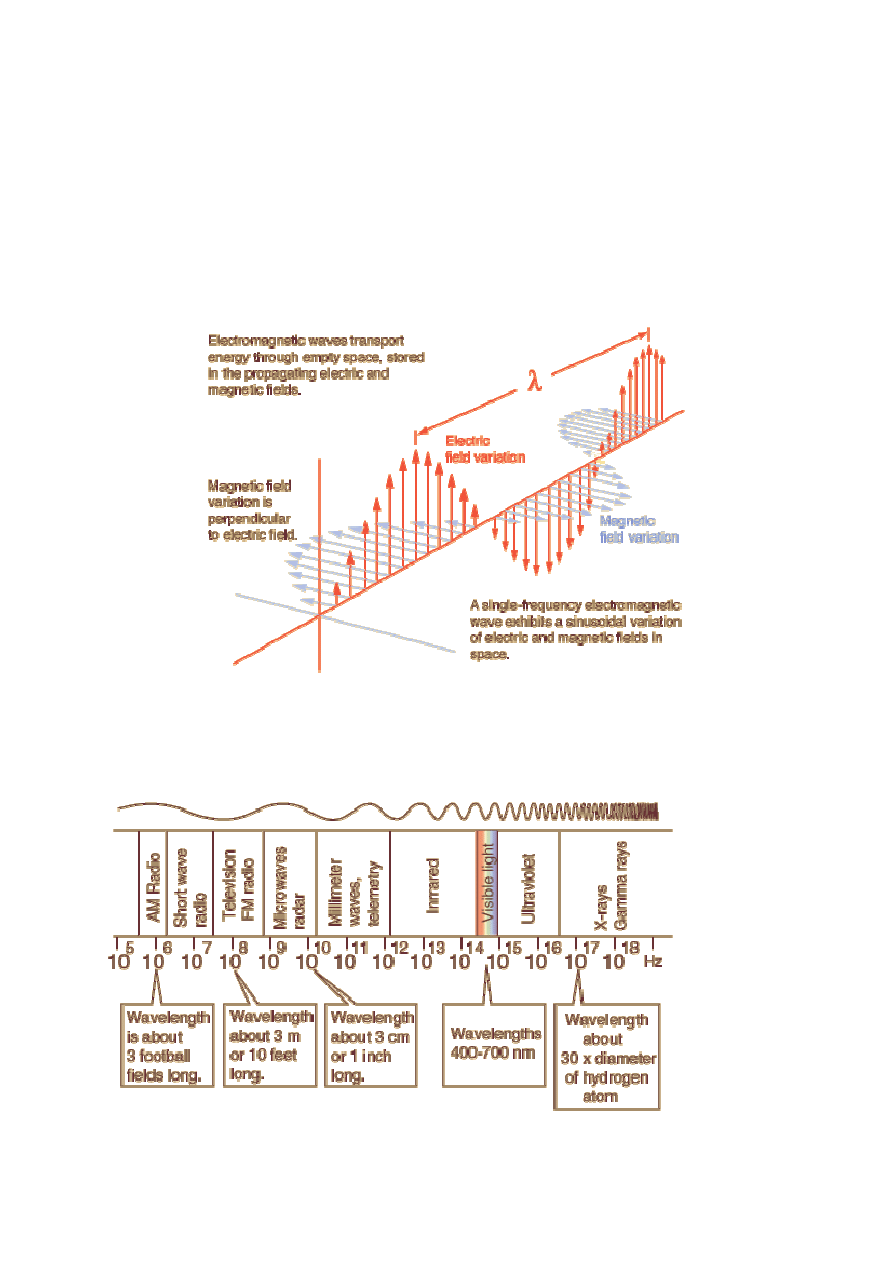
gdzie c – prędkość światła. Pole magnetyczne jest prostopadłe do pola
elektrycznego, zaś iloczyn wektorowy E x B wyznacza kierunek propagacji fali
elektromagnetycznej

Przykład fali elektromagnetycznej ukazuje rysunek poniżej.

Rys. Fala elektromagnetyczna

Widmo fal elektromagnetycznych

Rys. Fale elektromagnetyczne, spektrum.

9