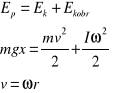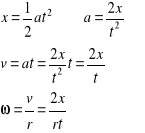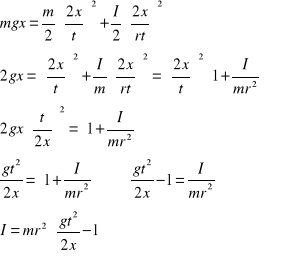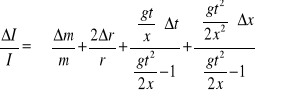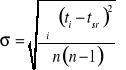Ćwiczenie nr 15

WYZNACZANIE MOMENTU BEZWŁADNOŚCI WAHADŁA MAXWELLA

1. Cel ćwiczenia

Wyznaczenie wartości momentu bezwładności wahadła Maxwella. Sprawdzenie zasady zachowania energii w ruchu postępowym i obrotowym.

2. Wprowadzenie

Wahadło Maxwella składa się z ciężkiego dysku o promieniu R umocowanego na osi o promieniu r (r <<R). Oś dysku jest zawieszona na dwóch nawiniętych na nią sznurkach. Sznurki zawieszone są równolegle do siebie na poprzeczce statywu (rys.15.1).

Rys. 15.1 Wahadło Maxwella

Nawijając sznurek dookoła osi podnosimy krążek na wysokość x. Jeśli go teraz puścimy swobodnie, odwijając się ze sznurka będzie opadał w dół i jednocześnie wykonywał ruch obrotowy.

Uwaga: w obliczeniach nie uwzględniono momentu bezwładności osi.

Jeżeli wahadło opuści się w dół i przebędzie drogę x to energia potencjalna E_p zamieni się na energię kinetyczną ruchu postępowego E_k i obrotowego E_kobr. Z zasady zachowanie energii wynika, że:

	(15.1)
		(15.2)
		(15.3)

gdzie:

v -prędkość liniowa krążka,

ω - prędkość kątową krążka,

I - moment bezwładności dysku ,m- masa krążka,

r - promień osi.

Oś obrotu krążka toczy się po sznurku, chwilowa oś obrotu jest styczna do osi i pokrywa się ze sznurkiem Moment siły M działający na krążek względem tej osi wynosi: M=mgr . Jest on stały w czasie, zatem z drugiej zasady dynamiki dla ruchu obrotowego wynika, że środek masy opada ruchem jednostajnie przyśpieszonym. Korzystając z równań ruchu jednostajnie przyśpieszonego:

	(15.4)
		(15.5)
		(15.6)

]

Podstawiając wielkości wyliczone w równaniach 15.4 -15,6 do równania 15.1 otrzymujemy:

	(15.7)
		(15.8)
		(15.9)
		(15.10)
		(15.11)

3. Opis stanowiska laboratoryjnego

Układ pomiarowy składa się z krążka z osią przechodzącą przez jego środek symetrii statywu z poprzeczką do zawieszanie krążka, sznurków do podwieszania krążka, stopera, przymiaru liniowego, suwmiarki, wagi elektronicznej.

4. Program ćwiczenia

1. Zdjąć krążek ze statywu i zważyć go- masa m, określić niepewność pomiaru masy Δm.

2. Zmierzyć średnicę osi 2r i ustalić niepewność jej pomiaru Δr.

3. Ustalić drogę opadania krążka x i jej niepewność pomiarową Δx. Pomiar przeprowadzamy w ten sposób, że bierzemy pod uwagę najniższy punkt krążka i mierzymy jego odległość od powierzchni stołu x₁. Następnie nawijamy starannie sznurek wokół krążka i ponownie mierzymy jego odległość od stołu x_2. Droga opadania x = x₂ - x₁

4. Nawinąć starannie sznurek wokół krążka i zmierzyć czas jego opadania t na drodze x . Ustalić jego niepewność systematyczną Δt. Czas opadania zmierzyć 20 razy. Obliczyć średnią arytmetyczna czasu opadania .Wyniki pomiarów umieścić w tabeli 15.1

Tabela 15.1

Δm= Δr= Δx₁= Δx₂= Δx= Δt=

Lp.	m[kg]	2r[m]	x1[m]	x2 [m]	Δx [m]	t [s]	tśr[s]

5. Sprawozdanie

1. Obliczyć ze wzoru [3] wartość momentu bezwładności I i porównać wartość doświadczalną z wartością teoretyczną. Zastanowić się, czy lepszą zgodność z teorią uzyskamy odejmując od obliczonej wartości I moment bezwładności samej osi.

2. Wyznaczyć maksymalną względną niepewność pomiarową, metodą różniczki zupełnej, ze wzoru:

(15.12)

lub ze wzoru uproszczonego:

(15.13)

Powyższą niepewność wyrazić również w procentach. Wyznaczyć również niepewność bezwzględną ΔI. Uwaga: wartość niepewności bezwzględnej ΔI otrzymujemy mnożąc wyliczoną niepewność względną pomiaru ΔI/I przez otrzymaną doświadczalnie wartość I.

3. Na podstawie wzoru podanego w punkcie 2 lub 3 sprawdzić, który z członów równania ma największy wpływ na wartość ΔI/I.

4. Przy wielokrotnych pomiarach tej samej wielkości czasu opadania t na ustalonej drodze x wskazane jest wyliczenie odchylenia standardowego σ wartości średniej czasu t_śr :

(15.14)

gdzie:

t_i - wartość i-tego pomiaru,

t_śr - średnia arytmetyczna,

n - ilość pomiarów

5. jeżeli wartość σ jest porównywalna z Δt całkowitą niepewność pomiaru

czasu Δt_cał określić ze wzoru:

(15.15)

6. Przeprowadzić dyskusje wyników i niepewności pomiarowych.

6. Pytania kontrolne

1. Ruch jednostajnie zmienny.

2. II zasada dynamiki w ruchu postępowym i obrotowym.

3. Moment siły, moment bezwładności, moment pędu.

4. Zasada zachowania energii. Rodzaje energii mechanicznej.

100

---