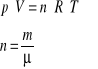Ćwiczenie nr 27

Sprawdzanie praw gazu doskonałego. Przemiana izotermiczna.

1. Cel ćwiczenia

Celem ćwiczenia jest badanie przemiany izotermicznej i sprawdzenie prawa

Boyle`a-Mariotte`a.

2. Wprowadzenie

Gaz doskonały składa się z jednakowych cząsteczek o pomijalnie małej objętości, poruszających się w chaotycznym ruchu. Zakłada się, że cząsteczki gazu oddziaływają ze sobą jedynie w chwili zderzenia. Zderzenia cząsteczek ze sobą i ściankami naczynia są doskonale sprężyste. Gazy rzeczywiste tylko dla niezbyt dużych ciśnień i temperatur stosują się do tego modelu. Z kinetyczno-molekularnej teorii gazów (teoria mikroskopowa) wynika, że iloczyn ciśnienia p i temperatury bezwzględnej T jest proporcjonalny średniej energii kinetycznej cząsteczek gazu:

(27.1)

gdzie:

N - ilość cząsteczek gazu,

E_{k śr} - średnia energia kinetyczna cząsteczek.

Z teorii kinetyczno molekularnej wynika również, że średnia energia kinetyczna

E_{k śr} jest proporcjonalna do temperatury bezwzględnej T. Wynika stąd równanie:

(27.2)

Dla stałej masy gazu m powyższe równania są zgodne z fenomenologicznym (makroskopowym) równaniem Clapeyrona:

	(27.3)
		(27.4)

gdzie:

R - uniwersalna stała gazowa,

n - ilość moli gazu,

m - masa,

μ - masa cząsteczkowa.

Gaz, który spełnia równanie Clapeyrona nazywamy gazem doskonałym. Makroskopowe wielkości ciśnienie p, objętość V i temperaturę termodynamiczna T nazywamy parametrami stanu gazu. Przemianami stanu gazu nazywamy procesy prowadzące do zmiany wartości ciśnienia p, objętości V lub temperatury T.

W znanych przemianach gazowych dwa parametry ulegają zmianie, a trzeci pozostaje stały. Znamy następujące przemiany:

• izotermiczna (prawo Boyle`a-Mariotte`a) T = const

• izobaryczna (prawo Gay-Lussaca) p =const

• izochoryczna (prawo Charlesa) V = const

• adiabatyczna- brak wymiany ciepła z otoczeniem

Aby zbadać przemianę izotermiczną posługujemy się przyrządem pokazanym schematycznie na rysunku 27.1.

Rysunek 27.1 Układ do sprawdzenia prawa Boyle`a-Mariotte`a

Jeżeli zawór Z jest otwarty nad cieczą w obu rurkach panuje jednakowe ciśnienie atmosferyczne p_a. Zamknięcie zaworu spowodowało zamknięcie nad cieczą stałej masy powietrza m. Jeżeli doświadczenie przeprowadzamy w stałej temperaturze T to zgodnie z równaniem Clapeyrona iloczyn pV pozostaje stały. Podniesienie lub obniżenie prawego ramienia przyrządu powoduję zmianę objętości słupa powietrza zamkniętego pod zaworem, a zgodnie z prawem Boyle`a-Mariotte`a również zmianę jego ciśnienia.

3. Opis stanowiska laboratoryjnego

Przyrząd wykorzystywany do sprawdzenia przemiany izotermicznej (rysunek 27.1.) składa się z dwóch rurek szklanych, o jednakowym i znanym przekroju poprzecznym, połączonych przewodem z tworzywa sztucznego. Rurki umocowane są do drewnianego statywu przy pomocy obejm, które umożliwiają podnoszenie lub opuszczanie rurek. Rurki są wypełnione rtęcią lub galistanem. Pomiędzy rurkami umieszczono linijkę, dzięki której możemy kontrolować poziom cieczy w rurkach. Jedna z rurek posiada na końcu zawór służący do zamykania słupa powietrza, a druga posiada otwarty koniec. Dodatkowo w pracowni należy umieścić barometr i termometr pokojowy.

4. Program ćwiczenia

1. Otworzyć zawór i ustawić poziom rtęci w rurkach na jednakowym poziomie. Najlepiej ustawić rtęć w połowie wysokości rurki. O ile nie podano średnicy wewnętrznej rurki d = 2r zmierzyć ją suwmiarką.

2. Zamknąć zawór.

3. Odczytać wartość ciśnienia atmosferycznego na barometrze p_a i temperaturę panująca w laboratorium t. Jeżeli zachodzi taka potrzeba zamienić jednostki odczytanego ciśnienia na mm słupa rtęci (mm Hg).

4. Odczytać i zanotować wysokość słupa powietrza w rurce, do której zamontowano zawór l₀. Umownie przyjęto, że kranik znajduje się w lewej rurce.

5. Podnieść prawą otwartą rurkę w górę o parę centymetrów. Zanotować wysokość słupa powietrza l₁ w rurce zamkniętej zaworem oraz różnicę poziomów rtęci w obu ramionach h₁.

6. Jeżeli przy zamkniętym zaworze podniesiemy prawe ramię poziom cieczy w lewym ramieniu opadnie zwiększając wysokość słupa powietrza. Różnica wysokości słupków cieczy h₁ oznacza nadwyżkę ciśnienia ponad wartość ciśnienia atmosferycznego. Aktualne ciśnienie zamkniętego słupa powietrza zapisujemy w postaci:

p1= pa+h1

(27.5)

7. Podnosić dalej prawą rurkę i powtórzyć czynności z punktów 5 i 6 dla 6 różnych wysokości prawej rurki.

8. Powtórzyć czynności z punktu 1.Jeżeli nie uda się ponownie ustawić słupków cieczy, równo na poprzednim, co w punkcie 1 poziomie, otworzyć zawór i zmieniając położenie rurek ponownie zrównoważyć wysokość poziomu cieczy w obu ramionach.

9. Ponownie zamknąć zawór i obniżyć otwartą prawą rurkę o kilka centymetrów.. Zanotować wysokość słupa powietrza l₂ w rurce zamkniętej zaworem oraz różnicę poziomów rtęci w obu ramionach h₂.

10. Jeżeli przy zamkniętym zaworze obniżymy prawe ramię poziom cieczy w lewym ramieniu podniesie się zmniejszając wysokość słupa powietrza. Różnica wysokości słupków cieczy h₂ oznacza o ile wartość ciśnienia atmosferycznego p_a jest mniejsza od ciśnienia zamkniętego słupa powietrza. Aktualne ciśnienie zamkniętego słupa powietrza zapisujemy w postaci:

p2= pa-h2

(27.6)

Opuszczać dalej prawą rurkę i powtórzyć czynności z punktów 9 i 10 dla 6 różnych wysokości prawej rurki.

11. Ustalić i zanotować systematyczne niepewności pomiarów bezpośrednich.

12. Wyniki pomiarów umieścić w tabeli 27.1

Tabela27. 1

t[⁰C]= T[K]= 2r [mm]= Δh₁ =Δh₂=Δh Δl= Δt= Δl=

Δd= Δ2r= Δl= Δp_a=

pa [mm Hg]
h1 [mm Hg]
p1 =pa+h1 [mm Hg]
l1 [mm]
h2 [mm Hg]
p2 =pa-h2 [mm Hg]
l2 [mm]

5. Sprawozdanie

1. Korzystając z tabeli pomiarowej obliczyć objętość powietrza zamkniętego w rurce dla wszystkich punktów pomiarowych V=Sl (powierzchnia przekroju rurki S=πd²/4). Ujednolicić jednostki.

2. Obliczyć metodą różniczki zupełnej maksymalną względną niepewność systematyczną pomiaru objętości ΔV/V ze wzoru:

(27.7)

3. Następnie obliczyć maksymalną bezwzględną niepewność systematyczną pomiaru objętości ΔV mnożąc obliczoną w punkcie 1 objętość przez wartość ΔV/V wyznaczoną w punkcie 2. Obliczenia przeprowadzić dla całego zakresu badanych ciśnień.

4. Uzyskane wyniki umieścić w tabeli.

5. Wykonać wykres ciśnienia p w funkcji objętości V p=f(V).Zaznaczyć niepewności pomiarowe Δp i ΔV. Jeżeli nie znamy średnicy rurek wystarczy wykreślić zależność ciśnienia od wysokości słupa powietrza l.

6. Wykonać wykres ciśnienia p w funkcji odwrotności 1/V p=f(1/V).Zaznaczyć niepewności pomiarowe Δp i 1/ΔV. Jeżeli nie znamy średnicy rurek wystarczy wykreślić zależność ciśnienia od odwrotności wysokości słupa powietrza 1/l.

7. Alternatywnie do punktu 6 można sporządzić wykres iloczynu ciśnienia i objętości pV w funkcji objętości V pV=f(V). Jeżeli nie znamy średnicy rurek wystarczy wykreślić zależność iloczynu ciśnienia i długości słupa powietrza od wysokości słupa powietrza l. Iloczyn pV lub pl można podać w jednostkach umownych.

8. Przeprowadzić dyskusję wyników i niepewności pomiarowych

6. Pytania kontrolne

1. Gaz doskonały.

2. Podstawowy wzór kinetycznej teorii gazów.

3. Równanie Clapeyrona.

4. Rodzaje przemian gazowych.

5. Gaz doskonały a gazy rzeczywiste.

170

---