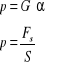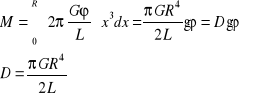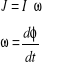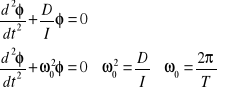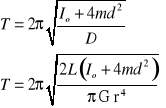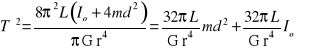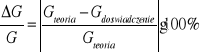Ćwiczenie nr 14

WYZNACZANIE WSPÓŁCZYNNIKA SZTYWNOŚCI G
NA SKRĘCANIE POPRZEZ POMIAR ZALEŻNOŚCI OKRESU DRGAŃ WIBRATORA W FUNKCJI MOMENTU BEZWŁADNOŚCI (METODA DYNAMICZNA GAUSSA)

1. Cel ćwiczenia

Badanie odkształcenia postaci drutu stalowego.Wyznaczenie współczynnika sztywności G (modułu sztywności) drutu stalowego.

2. Wprowadzenie

W wyniku działania sił zewnętrznych ciała stałe ulegają odkształceniu. Zmiana kształtu (odkształcenie postaci) ciała stałego może nastąpić między innymi na skutek wydłużania (skracania), ścinania (efekt przyłożenia siły stycznej do krawędzi ciała), skręcenia (zwłaszcza dla prętów i drutów),zginania( belki i pręty).

Po usunięciu sił zewnętrznych ciało może powrócić do pierwotnego kształtu i objętości.

Takie odkształcenie nazywamy sprężystym. W wyniku przekroczenia granicznej wartości siły zewnętrznej ciało nie odzyskuje pierwotnego kształtu i pozostaje trwale odkształcone. Dla małych odkształceń zmienia się kształt ciał, ale bez zmiany objętości.

Równanie opisujące zależność pomiędzy naprężeniem wewnętrznym σ wywołanym przez siły zewnętrzne F a odkształceniem względnym ε nosi nazwę równania Hooke`a:

(14.1)

σ - jest naprężeniem wewnętrznym normalnym lub stycznym.

(14.2)

Jednostką naprężenia jest N/m² lub paskal [Pa], czyli jednostki ciśnienia. Naprężenie normalne występuje wówczas, gdy siła działa prostopadle do powierzchni S, a siła działająca stycznie do powierzchni powoduje naprężenia styczne. Odkształcenie względne ε jest równe stosunkowi odkształcenia bezwzględnego Δx do początkowej wartości x₀ określającej początkowe rozmiary lub kształt ciała:

(14.3)

K jest modułem sprężystości, zależnym od rodzaju odkształcenia.

Celem ćwiczenia jest wyznaczanie współczynnika sztywności drutu stalowego niepodlegającego trwałemu odkształceniu.

Jeżeli na jeden z boków sześcianu działa siła styczna F_s to spowoduje ona powstanie w materiale naprężenia stycznego p (rysunek 14.1). Prawo Hooke'a ma wówczas postać:

	(14.4)
		(14.5)

gdzie:

p - naprężenie styczne

S - powierzchnia boku wzdłuż której działa siła styczna F_s

α - kąt skręcenia (ścinania) o który przesuną się krawędzie poddane działaniu zewnętrznej siły stycznej F_s.

Rolę odkształcenia względnego pełni wówczas kąt ścinania α wyrażony w mierze łukowej. Współczynnik proporcjonalności G nosi nazwę modułu sztywności i ma wymiar Nm^-2. Moduł sprężystości G przyjmuje wartości od 1/3 do ½ modułu Younga E.

Rys.14.1 Odksztalcenia ciała przy działaniu sił stycznej

W celu wyznaczenia modułu sztywności G drutu o długości L , przekroju poprzecznym S i umocowanego na jednym z jego końców rozważmy moment sił M działających działający na drugi z końców pręta, powodujący jego skręcenie o kąt φ. Można założyć że drut składa się z cienkich tulejek o długości L, promieniu r
i grubości dx. Odkształcenia poszczególnych tulejek rosną proporcjonalnie do wartości promienia r. Jednocześnie elementy tulejki równoległe do osi drutu ulegają skręceniu o kąt α i przybierają kształt linii śrubowych (rysunek 14.2).

Rys. 14.2 Odksztalcenie pręta przy działaniu momentów sił

Moment siły dM działający na wydzieloną warstwę dx o promieniu x wyraża się wzorem:

(14.6)

Dla wydzielonej warstwy dx naprężenie styczne wyraża się wzorem:

(14.7)

Element dS wydzielonej powierzchni można zapisać wzorem:

(14.8)

Podstawiając równania (14.7) i (14.6) do równania (14.5)otrzymujemy związek:

(14.9)

Dla małych kątów α skręcenia drutu otrzymujemy :

(14.10)

Po podstawieniu równania (14.9) prawo Hooke'a przyjmuje postać:

(14.11)

Zaś moment sił skręcających dM :

(14.12)

Po obustronnym scałkowaniu w granicach od 0 do R równania (14.12) otrzymujemy całkowity moment sił M wynosi:

	(14.13)
		(14.14)

Wyrażenie D jest dla danego pręta wielkością stałą. Nosi ono nazwę momentu kierującego D.

Skręcenie nieumocowanego końca drutu o kąt φ spowoduje powstanie sił sprężystości, których moment M, jest skierowany przeciwnie do momentu sił skręcających i zgodnie z prawem Hooke`a jest proporcjonalny do kąta skręcenia drutu:

(14.15)

gdzie:

ϕ -kąt skręcenia wyrażony w mierze łukowej kąta.

Aby uzyskać znaczące skręcenie drutu umieszczamy na jego końcu tzw. wibrator. Składa się on z dwóch prostopadłych prętów, na które założono cztery ciężarki o jednakowej masie m. Całkowity moment bezwładności wibratora można zapisać wzorem:

(14.16)

gdzie:

I_o - moment bezwładności nieobciążonego wibratora

4md² - moment bezwładności 4 ciężarków umocowanych na prętach w jednakowych odległościach d od osi obrotu.

Drut wraz z wibratorem wychylony z położenia równowagi nazywamy wahadłem torsyjnym. Moment siły M powoduje drgania harmoniczne drutu starając się przywrócić go do stanu równowagi. Z drugiej strony zgodnie z II zasadą dynamiki dla ruchu obrotowego ciała sztywnego:

(14.17)

gdzie L oznacza moment pędu wyrażony wzorem:

	(14.18)
		(14.19)

ω - prędkość kątowa w ruchu obrotowym dookoła ustalonej osi obrotu. W ćwiczeniu kierunek wektora ω pokrywa się z kierunkiem osi drutu.. Moment siły M można zapisać w postaci skalarnej:

(14.20)

po przekształceniu powyższego równania otrzymujemy równanie ruchu:

	(14.21)
		(14.22)

Rozwiązaniem tego równania jest funkcja periodyczna typu sinus lub cosinus:

(14.23)

gdzie:

φ(t) - wychylenie kątowe z położenia równowagi po czasie t,

φ_o - amplituda czyli maksymalne wychylenie,

ω_o - częstość kątowa drgań,

T - okres drgań,

α_o - faza początkowa drgań.

Kąt φ wyrażamy w radianach. Okres T drgań torsyjnych zapisujemy wzorem:

(14.24)

Pomiar okresu wahadła torsyjnego umożliwia wyznaczenie momentu kierującego D, a następnie modułu sztywności G.W opisywanym ćwiczeniu okres drgań układu opisujemy wzorem:

	(14.25)
		(14.26)

Po podniesieniu powyższego równania do kwadratu otrzymujemy zależność pomiędzy kwadratem okresu drgań T² wibratora a odległością d ciężarków m od osi obrotu:

(14.27)

Otrzymaliśmy równanie liniowe y = ax + b, gdzie:

(14.28)

3. Opis stanowiska laboratoryjnego

Stanowisko laboratoryjne pokazano na rysunku 14.3.

Zawiera ono stalowy drut o średnicy 2r i długości L zamocowany trwale na jednym końcu. Drugi koniec zamocowany jest w uchwycie wahadła torsyjnego w kształcie krzyżaka, na ramionach, którego umieszczone są równomiernie cztery ciężarki o jednakowych masach m. Pod spodem wahadła umieszczono masywny obciążnik Ob.Moment bezwładności I układu zmieniamy przesuwając równomiernie ciężarki m względem osi obrotu wahadła torsyjnego. Potrzebne przyrządy: stoper, śruba mikrometryczna lub suwmiarka,

przymiar liniowy, waga.

Rys.14.3 Stanowisko laboratoryjne do wyznaczania modułu sprężystości G

4. Program ćwiczenia:

1. Wyznaczyć i zapisać długość drutu L. Zanotować niepewność pomiarową pomiaru ΔL.

2. Zmierzyć i zanotować średnicę drutu 2r. Zanotować wartość niepewności Δ(2r).

3. Zważyć masy m i ustalić ich niepewność pomiarową Δm.

4. Ustawić równomiernie masy m w położeniu d najbliższym osi obrotu. Odległość d mierzymy od środka drutu do środka masy ciężarka. W tabeli 14.1 zanotować wartość d i niepewność Δd.

5. Skręcić drut o niewielki kąt i wprowadzić wibrator w drgania. Za pomocą stopera zmierzyć czas t dla n=10 okresów drgań torsyjnych T (n=10 okresów T). Dla danego momentu bezwładności ( ustalonego położenia 4 ciężarków) czynność powtórzyć minimum 2 razy. Zanotować niepewność pomiarową Δt i ΔT= Δt/n . Wyniki zapisać w tabeli 14.1.

6. Powyższą czynność powtórzyć dla przynajmniej 8 kolejnych odległości d od osi obrotu.

Tabela 14.1.

Δt= ΔT = Δt/n T_śr= t_śr//n

l.p.

L [m]

ΔL [m]

2r [m]

Δ(2r) [m]

d [m]

Δd [m]

2d Δd [m^2]

t1 [s]

t2 [s]

tśr [s]

Tśr [s]

ΔT [s]

2T ΔT [s^2]

5. Sprawozdanie

1. Na zajęciach korzystając z programu regresja liniowa lub z arkusza kalkulacyjnego Excel sprawdzić liniowość wykresu T² = f(d² ) oraz zapisać wyliczone przez program współczynniki a, b, Sa, Sb i współczynnik korelacji r.

2. Na papierze milimetrowym lub korzystając z kreatora wykresu wykonać wykres T² = f(d² ) zaznaczając na wykresie prostokąty niepewności pomiarowych 2TΔT , 2dΔd . W przypadku wykresu wykonanego na papierze milimetrowym poprzez maksymalną ilość prostokątów poprowadzić .Z wykresu wyznaczyć współczynnik kierunkowy prostej

ad = (32 π mL/Gr^4

(14.29)

a następnie wyliczyć szukany moduł sztywności drutu

G = (32 π mL/ ad r^4)

(14.30)

Indeks d oznacza wartość doświadczalną wyznaczonego

współczynnika kierunkowego a_d .

3. Znaleźć w literaturze moduł sztywności dla stali i wyznaczyć niepewność względną względem wartości tabelarycznej.

(14.31)

4. Przeprowadzić dyskusję otrzymanych wyników i niepewności pomiarowych.

6. Pytania kontrolne

1. Drgania harmoniczne proste i tłumione.

2. Wykresy wychylenia, prędkości i przyspieszenia w ruchu harmonicznym.

3. Podaj przykłady układów spełniających warunek ruchu harmonicznego.

4. Definicja bryły sztywnej i momentu bezwładności.

5. II zasada dynamiki dla ruchu obrotowego, zasada zachowania momentu pędu.

Twierdzenie Steinera.

95

---