Nr ćwiczenia: 310	Data: 14-03-2001r.	Marek Frątczak		Wydział Elektryczny	Semestr II	Grupa: E-9
Prowadzący: mgr inż. Jarosław Gutek			Przygotował: Marek Frątczak	Wykonał: Marek Frątczak	Opracował: Marek Frątczak	Ocena:

Temat: Wyznaczanie współczynnika załamania światła z pomiaru pozornej i rzeczywistej grubości płytek.

1. Wstęp teoretyczny.

Światło, które po drodze wpada do naszego okna przechodzi przez przynajmniej jedną powierzchnię załamującą, ma na ogół inny kierunek, niż gdyby biegło po linii prostej, w ośrodku jednorodnym. Efektem tego jest to, iż obserwator odnosi wrażenie, że światło wychodzi z innego źródła niż to jest w rzeczywistości. Obserwowane źródło jest obrazem źródła rzeczywistego lub źródłem pozornym.

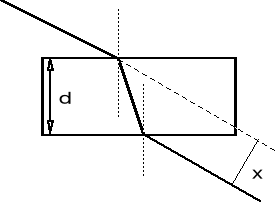
Przy przejściu światła przez płytkę równoległościenną dwukrotnie zachodzi zjawisko załamania światła, w wyniku czego otrzymujemy promień równoległy do początkowego odchylony o x, gdzie:

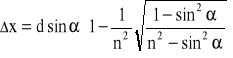
Spoglądając na przedmioty leżące na dnie naczynia z wodą wydaje nam się, leżą one bliżej powierzchni niż w rzeczywistości. . Przeciwnie, nurek spoglądający w górę na, powiedzmy zwisającą gałąź drzewa będzie sądzić, że jest ona wyżej niż w rzeczywistości wynikającą z załamania światła na granicy dwóch ośrodków.

Podstawa fizyczna metody

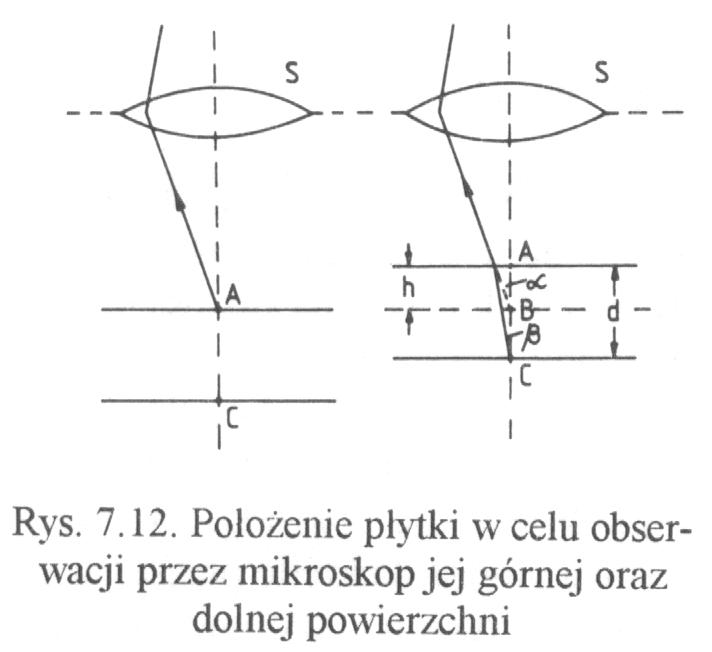
Przykład zjawiska, w którym występuje pozorna zmiana grubości, a także zasadę pomiaru tej grubości ilustruje rysunek. W lewej części rysunku widzimy soczewkę S (może nią być okular mikroskopu) ustawioną w ten sposób, że w ustalonym miejscu, niewidocznym na rysunku, powstaje ostry obraz punktu A znajdującego się na górnej powierzchni płytki.

Chcąc uzyskać ostry obraz punktu C znajdującego się na dolnej powierzchni płytki (prawa część rysunku), musimy całą płytkę przesunąć ku górze o odległość h. W tym położeniu promień wybiegający z punktu C "widziany jest" przez soczewkę, jakoby wychodził z punktu B. W tym samym miejscu co poprzednio powstaje obraz pozornego źródła B, czyli rzeczywistego źródła C.

Według prawa załamania światła stosunek sinusów kątów padania
i kąta załamania
jest dla danej pary ośrodków wielkością stałą, równą stosunkowi bezwzględnych współczynników załamania ośrodków.

Wartość bezwzględnego współczynnika załamania otrzymujemy z powyższego równania, gdy jednym z ośrodków jest próżnia (n₁=1). Prawo załamania światła na granicy próżnia - ośrodek, a także w przybliżeniu na granicy powietrze - ośrodek przyjmuje wtedy postać

gdzie n oznacza bezwzględny współczynnik załamania dowolnego ośrodka.

W celu obliczenia pozornej grubości h zakładamy, że promienie biegnące w płytce tworzą bardzo mały kąt z prostopadłą padania. W tej sytuacji możemy zastąpić sinusy kątów samymi kątami

,

.

Wstawiając powyższe wartości otrzymujemy związek między grubością pozorną h i rzeczywistą d

gdzie h = ad - ag.

2. Opis przeprowadzonego ćwiczenia.

• Zmierzyć grubość rzeczywistą wszystkich przeznaczonych do pomiaru płytek.

• Ustawić płytkę na stoliku mikroskopu.

• Znaleźć położenie stolika mikroskopu ad, przy którym widać wyraźnie rysę dolną, a następnie położenie ag, przy którym powstaje wyraźny obraz rysy górnej.

• W razie potrzeby powtarzać pomiar, każdorazowo „psując” obraz i szukając na nowo właściwego położenia stolika.

• Obliczyć wartości średnie grubości rzeczywistej i pozornej.

• Obliczyć współczynnik załamania.

3. Dane eksperymentalne.

• grubość rzeczywista d [mm]

L.p.	Płytka 1 [mm]	Płytka 2 [mm]
1	4.02	3,84
2	4,03	3,85
3	4,01	3,83
4	4,01	3,85
5	4,02	3,84
6	4,03	3,83
7	4,01	3,84
8	4,02	3,84
9	4,03	3,85
10	4,01	3,84

d =  0,01 [mm]

• grubość pozorna h [mm]

h = ad - ag

h1 =3,63 - 1,16 = 2,47

	Płytka nr 1 [mm]			Płytka nr 2 [mm]
L.p.	ad	ag	h1	ad	ag	h2
1	3,63	1,16	2,47	3,95	1,62	2,33
2	3,45	1,11	2,34	3,95	1,67	2,28
3	3,52	1,10	2,42	3,99	1,68	2,31
4	3,56	1,05	2,51	3,99	1,48	2,51
5	3,49	1,04	2,45	3,90	1,40	2,50
6	3,46	1,03	2,43	3,90	1,49	2,41
7	3,47	1,00	2,47	3,91	1,49	2,42
8	3,70	1,14	2,56	3,91	1,54	2,37
9	3,74	1,17	2,57	3,90	1,39	2,51
10	3,59	1,07	2,52	3,89	1,40	2,49

h = 0.01 [mm]

n1 = 1,6275

	Płytka1	Płytka2
n1	1,6275	1,6480
n2	1,7179	1,6842
n3	1,6611	1,6623
n4	1,6015	1,5298
n5	1,6408	1,536
n6	1,6543	1,5933
n7	1,6275	1,5867
n8	1,5703	1,6202
n9	1,5642	1,5298
n10	1,5952	1,5421
n	1,6256	1,5929

4. Obliczenia rachunkowe błędów.

• Dla pomiarów grubości rzeczywistej d:

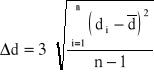
	Płytka nr 1 [mm]	Płytka nr 2 [mm]
	4,019	3,841
	0,011	0,009
	4,020,01	3,840,01

• Dla pomiarów grubości pozornej h:

h = ad - ag

∆h = ½∆ad + ½∆ag

	p³ytka nr 1[mm]	p³ytka nr 2 [mm]
	2,474	2,413
	0,389	0,412
	2.470,42	2,410,34

• Dla wartości współczynnika n:

	płytka nr 1	płytka nr 2
	1,6259	1,5929
	0,0781	0,0763
n	1,630,09	1,590,07

5. Końcowe zestawienie wyników.

• płytka 1

n = 1.63 0,09

• płytka 2

n = 1,59 0,07.

6. Wnioski.

Pomiary które zostały przeprowadzone przy użyciu mikroskopu i miarki w nim zainstalowanej są obarczone pewnym błędem, ze względu na brak możliwości regulacji pokrętłem precyzyjnym, a jedynie pokrętłem zgubnym. . Można jednakże pokusić się o próbę zidentyfikowania materiałów z których płytki zostały wykonane. Płytka nr1 została najprawdopodobniej wykonana ze szkła flint ciężkiego ( n=1,6359). Płytka nr 2 została wykonana z pleksiglasu ( n= 1,5929).

---