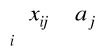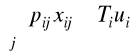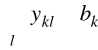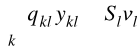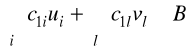ESP - pojęcia podstawowe

1.1. Rodzaje ESP

Elastyczny system produkcyjny
(ESP czasami FMS - Flexible Manufacturing System)

zespól sterowanych numerycznie obrabiarek CNC zintegrowanych poprzez zautomatyzowany transport i magazynowanie oraz wspólne sterowanie komputerowe.

Składowe ESP

• Maszyny i urządzenia produkcyjne

• obrabiarki numerycznie sterowane,

• maszyny pomiarowe CNC.

• Urządzenia transportowe

• roboty przemysłowe;

• wózki automatycznie kierowane radiowo, przewodowe, szynowo itp.

• transportery, przenośniki karuzelowe, zmieniacze palet;

• suwnice, układnice regałowe.

• Magazyny

• zautomatyzowany magazyn centralny (AS/RS);

• magazyny lokalne;

• bufory międzyoperacyjne przy obrabiarkach.

• Sieć nadzorujących komputerów i mikroprocesorów

Funkcje:

• kierowanie marszrutami przepływu części;

• śledzenie stanu wykonania wytwarzanych części tak, aby w każdej chwili wiadomo było gdzie daną część należy skierować w celu wykonania następnej operacji;

• przekazywanie instrukcji wykonania poszczególnych operacji do maszyn z jednoczesnym zabezpiecze­niem dostępności niezbędnych narzędzi;

• nadzorowanie prawidłowości wykonywania operacji i sygnalizowanie zdarzeń wymagających interwencji.

Typy podstawowe ESP

Cechy ESP:

• uniwersalności maszyn (każda maszyna może wykonywać wiele różnych operacji);

• jednoczesne wytwarzanie w systemie różnych typów części;

• możliwość wytwarzania części każdego typu przy zastosowaniu różnych marszrut przepływu;

• niewielki "luzy" wynikające ze wzajemnych powiązań elementów i sterowania w czasie rzeczywistym.

Efektywne wykorzystanie ESP zależy od właściwego doboru strategii planowania, harmonogramowania i operatywnego sterowania produkcji.

Elastyczne gniazdo produkcyjne Murata Machinery Ltd

1 - centrum obróbkowe CNC, 2 - zmieniacz narzędzi, 3 - stanowisko załadunku / wyładunku palet, 4 - przenośnik palet, 5 - lokalny magazyn narzędzi, 6 - manipulator do wymiany narzędzi, 7- wózek AGV, 8 - centralny magazyn AS/RS, 9 - automatyczna układnica regałowa

1.2 Elastyczność i rodzaje elastyczności

Rodzaje elastyczności

1.3. Korzyści ze stosowania ESP

Projektowanie wyrobów, planowanie produkcji, harmonogramo­wanie, sterowanie procesem, gospodarka narzędziowa stanowią jeden system. Powoduje to:

• Skrócenie całkowitego czasu realizacji partii produkcyjnej w porównaniu z konwencjonalnym systemie produkcyjnym.

• Zminimalizowanie wielkości produkcji w toku.

• Skrócenie czasu koniecznego do zmiany asortymentu produkcji.

• Lepsze powiązanie z systemem planowania i harmonogramowania.

• Lepsze wykorzystanie maszyn dzięki zastosowaniu nowoczes­nych metod harmonogramowania i bieżącego sterowania produkcji.

• Wysoki stopień automatyzacji w elastycznych systemach produkcyjnych w porównaniu z innymi sposobami wytwarzania umożliwia:

• Redukcję personelu.

• Ujednolicenie i poprawę jakości produktu finalnego (wszystkie części finalnego produktu będą miały jakość taka sama dla każdego elementu - o jakości złożonego produktu decyduje jego najsłabszy element).

1.4. Trudności w stosowaniu ESP

!	Największą trudnością jest wyważony kompromis pomiędzy elastycznością systemu, a jego wydajnością

Czynniki wpływające na wydajność ESP:

• Wszystkie części przed wprowadzeniem do systemu muszą być zamocowane na paletach. Uchwyty są drogie i zwykle przeznaczone do mocowania ograniczonego zestawu typów części. W związku z tym często stosuje się jedno z następujących alternatywnych rozwiązań:

• liczba produkowanych części jest ograniczona;

• w systemie utrzymywana jest duża liczba różnych uchwytów;

• używa się uchwytów uniwersalnych, które mogą być adaptowane do aktualnie obrabianych części (przygotowanie uchwytu dla zmieniającego się asortymentu produkcji zabiera dużo czasu).

• Pojemność lokalnych magazynków narzędzi przy obrabiarkach jest ograniczona. Może się zdarzyć, że zaplanowana operacja nie jest wykonywana, jeśli odpowiednie narzędzia nie zostały załadowane przed rozpoczęciem produkcji.

• Zadania produkcyjne powinny być tak dobrane, by równomiernie obciążały pracą wszystkie obrabiarki.

1.5. Kierunki rozwoju ESP

Funkcje realizowane w systemie:

1. Projektowanie części i wyrobów.

2. Projektowanie narzędzi i uchwytów.

3. Planowanie procesów technologicznych.

4. Programowanie sterowanych numerycznie maszyn, robotów, systemów transportu itd.

5. Planowanie produkcji.

6. Harmonogramowanie produkcji.

7. Obróbka mechaniczna części.

8. Montaż.

9. Transport i magazynowanie.

10. Kontrola jakości.

11. Utrzymywanie sprawności maszyn i urządzeń systemu.

W ESP wiodącą rolę odgrywa komputer i wspomaganie lub bezpośrednie sterowanie komputerowe.

Systemy wspomagania komputerowego:

CAD (Computer Aided Design)	System wspomagania projektowania funkcje (1),(2);
CAPP (Computer Aided Process Planing)	System wspomagania planowania procesu technologicznego funkcja (3);
CAM (Computer Aided Manufacturing)	System wspomagania wytwarzania funkcje (4),(5),(6),(7),(8),(11);
CAQC (Computer Aided Quality Control)	System wspomagania kontroli jakości funkcja (10);
AS/RS (Automated Storage / Retrieval System)	Zautomatyzowany system magazynowania funkcja (9).

Projektowanie ESP

Projektowanie jest procesem iteracyjnym: wymaga rozwiązania wielu wzajemnie powiązanych zadań, tworzących wielopoziomową strukturę hierarchiczną.

Dobór wyposażenia sprzętowego

Obejmuje zadania, rozwiązywane jednocześnie lub kolejno:

• dobór maszyn (obrabiarek),

• dobór środków transportu.

!	Na dobór sprzętu mają wpływ nie tylko typy części i operacji przewidywane do wykonywania, ale również rodzaj zastosowanego rozmieszczenia maszyn.

Oznaczenia

i indeks typu maszyny, i
I

j indeks typu operacji, j
J

k indeks typu części, k
K

l indeks typu urządzenia transportowego, l
L

a_j liczba operacji j, którą należy wykonać

b_k liczba części k, którą należy wyprodukować

B całkowity budżet na zakup wyposażenia ESP

c_1i koszt zakupu maszyny i

c_2l koszt zakupu urządzenia transportowego

g_ij koszt wykonania operacji j na maszynie t

h_kl koszt transportu części k za pomocą urządzenia l

p_ij czas wykonywania operacji j na maszynie i

q_lk czas transportu części k za pomocą urządzenia l

S_l czas dysponowany urządzenia transportowego l

T_i czas dysponowany maszyny l

u_i zmienna decyzyjna - liczba zakupionych maszyn i

v_l zmienna decyzyjna - liczba zakupionych urządzeń transportowych l

x_ij zmienna decyzyjna - liczba operacji j przydzielonych do maszyny i

y_kl zmienna decyzyjna - liczba części k transportowanych za pomocą urządzenia l

Zadanie doboru wyposażenia sprzętowego jako problem programowania całkowitoliczbowego:

Model M2.1

Zminimalizować (łączne koszty zakupu, koszty produkcji i transportu)

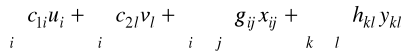
(2.1)

przy ograniczeniach

zapewnienie wykonania wszystkich operacji		(2.2)
zabezpieczenie przed przekroczeniem dyspono­wanych czasów maszyn		(2.3)
zapewnienie transportu wszystkich części		(2.4)
zabezpieczenie przed przekroczeniem dysponowanych czasów środków transportu		(2.5)
zabezpieczenie przed przekroczeniem dysponowanego budżetu		(2.6)
		całkowite nieujemne wielkości (2.7)

Optymalizacja konfiguracji przestrzennej systemu

Jest to jednego z pierwszych zadań, które należy rozwiązać w początkowym etapie projektowania. Rozmieszczenie maszyn zależy od rodzaju zastosowanych środków transportu.

Rodzaje urządzeń transportowych w ESP

1. Wózki indywidualnie napędzane:

• Wózki automatycznie kierowane, AGV - samojezdne wózki kołowe zasilane z baterii akumulatorów, sterowane przez centralny komputer ESP;

• wózki szynowe;

• wózki holowane - wózki kołowe poruszające się po posadzce, ciągnione za pomocą napędzanego łańcucha zainstalowanego pod posadzką.

2. Przenośniki:

• rolkowe - przedmioty poruszają się po napędzanych rolkach;

• taśmowe - transportowane przedmioty poruszają się na taśmie napędzanej za pomocą rolek lub kół napędowych;

• pneumatyczne - z poduszką powietrzną, która podtrzymuje i transportuje małe przedmioty.

Roboty - suwnicowe lub zamontowane na wózkach.

Suwnice i układnice regałowe (w zautomatyz. magazynach).

Najczęściej stosowane są:

• wózki automatycznie kierowane (AGV) - maszyny przeważnie są ustawiane wzdłuż linii prostej w jednym lub większej liczbie rzędów.

• roboty stacjonarne - stosuje się kołowe rozmieszczenie maszyn

• roboty suwnicowe - maszyny również powinny być ustawione blisko siebie, tworząc tzw. rozmieszczenie grupowe

Jeżeli sieć transportowa ma postać zamkniętej pętli, w której przepływ materiałów jest jednokierunkowy, to mówi się o cyklicznym rozmieszczeniu maszyn (w przypadkach zastosowania przenośników karuzelowych, systemu jednoszynowego transportu podwieszonego, jednokierunkowego systemu wózków AGV kierowanych przewodowo).

Zadanie optymalizacji rozmieszczenia maszyn najczęściej jest formułowane jako tzw. kwadratowy problem przydziału, kwadratowy problem pokrycia lub problem optymalizacji na grafie.

Liniowe, jednorzędowe rozmieszczenie maszyn

Założenia:

• Maszyny są ustawione wzdłuż jednej linii prostej (drogi transportu),

• Orientacja przestrzenna maszyn jest taka sama.

Oznaczenia:

m - liczba maszyn,

a_i - długość maszyny i (i = l,..., m),

c_ij - koszt przejazdu wózka AGV (na jednostkę długości) od maszyny i do j,

d_ij - minimalny odstęp (prześwit) pomiędzy maszynami i oraz j,

f_ij - przepływy części (liczba przejazdów wózka) pomiędzy maszynami i oraz j,

x_i - odległość środka maszyny i od pionowej linii odniesienia.

Zadanie wyznaczenia liniowego, jednorzędowego rozmieszczenia maszyn jako zagadnienie PL.

Model M2.2

Zminimalizować (koszt przejazdu pomiędzy maszynami)

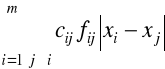
(2.11)

przy ograniczeniach (zachowanie wymaganych odstępów)

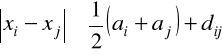
, i,j = 1-m, (2.12)

(2.13)

Model można sprowadzić do standardowej postaci zadania PL jak wprowadzić zmienne pomocnicze

,
.

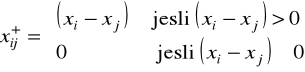
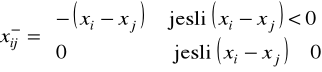
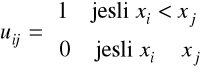
Z powyższych zależności wynika, że

,

Zadanie (2.11)-(2.13) można zastąpić następującym problemem programowania liniowego mieszanego:

Model M2.3

Zminimalizować

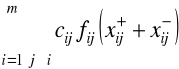
(2.14)

przy ograniczeniach

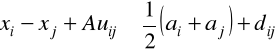
, i,j = 1-m, (2.15)

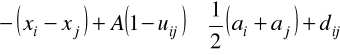
, i,j = 1-m, (2.16)

, (2.17)

,
,
(2.18)-(2.20)

A jest dostatecznie dużą stalą.

Rozwiązanie zadania (2.14) - (2.20) można wyznaczyć za pomocą algorytmów programowania calkowitoliczbowego.

Możliwe jest zastosowanie standardowych pakietów - LINDO, GAMS, itp.

!	W przypadku większej liczby maszyn (m > 20) zwykle stosuje się algorytmy heurystyczne

Algorytm generuje jedynie kolejność ustawienia maszyn.

Jeżeli środkiem transportu będzie robot, to maszyny należy ustawić wzdłuż okręgu;

W przypadku zastosowania wózków AGV maszyny powinny być ustawione wzdłuż linii prostej.

Liniowe, wielorzędowe rozmieszczenie maszyn

Rozważmy wariant uproszczony, w którym wszystkie maszyny mają jednakowe wymiary i podstawy w kształcie kwadratów.

Oznaczenie:

x_i - odległość pozioma (wzdłuż osi x) środka maszyny i od osi y;

y_i - odległość pionowa (wzdłuż osi y) środka maszyny i od osi x.

Model M2.4

Zminimalizować

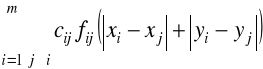
(2.21)

przy ograniczeniach

, i,j = 1-m, (2.22)

całkowite (2.23)

Jeżeli wymiary miejsca, na którym mają być ustawione maszyny również są ograniczone (długość D i szerokość S), to dodatkowo należy wprowadzić

,
, i,j = 1-m, (2.24) (2.25)

Problem (2.21) - (2.25) można sprowadzić do standardowej postaci zadania programowania całkowitoliczbowego

,

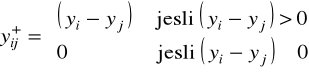
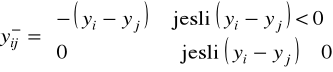
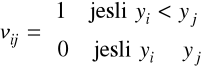
Problem (2.21) - (2.25) możemy zastąpić równoważnym zadaniem programowania liniowego mieszanego.

Model M2.5

Zminimalizować

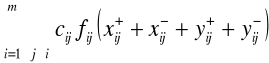
(2.26)

przy ograniczeniach

, i,j = 1-m, (2.27)

, (2.28)

, i,j = 1-m,
, (2.29)

,

(2.35)

(2.27) -(2.30) zapewniają zachowanie odstępów pomiędzy maszynami.

Ogólny przypadek rozmieszczenia w wielu rzędach maszyn o dowolnych wymiarach i podstawach w kształcie prostokątów.

a_i i b_i - długość i szerokość prostokąta podstawy

d_ij i e_ij - minimalne odstępy pomiędzy każdą parą maszyn wzdłuż obu wymiarów

Model M2.6

Zminimalizować

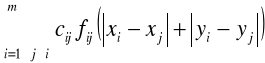
(2.36)

przy ograniczeniach

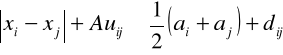
, i,j = 1-m,
(2.37)

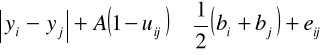
(2.38)

(2.40)

Model M2.7 (Zadanie programowania liniowego mieszanego)

Zminimalizować

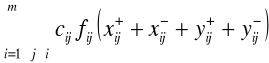
(2.41)

przy ograniczeniach

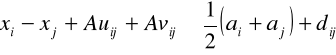
, i,j = 1-m, (2.42)

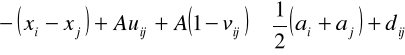
, (2.43)

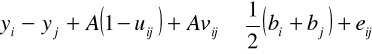
, i,j = 1-m,
(2.44)

,

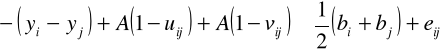
(2.50)

Cykliczne rozmieszczenie maszyn

W zależności od wzajemnego rozmieszczenia maszyn i wymaganych operacji wykonanie każdej części będzie wymagać okrążenia całej sieci co najmniej raz, a co najwyżej tyle razy ile różnych operacji należy wykonać.

Oznaczenia:

i - numer maszyny, i = l,..., m;

i = 0 - stanowisko załadunkowe/wyładunkowe;

f_ij - przepływ (liczba części) od maszyny i do maszyny j.

L

Rys. 2.8. Graf reprezentujący cykliczne rozmieszczenie m = 5 maszyn wraz ze stanowiskiem załadunkowym/wyładunkowym

T

Rys. 2.8. Reprezentacje grafowe cyklicznego rozmieszczenia maszyn

W grafie T łuk (i, j) występuje tylko wtedy, gdy w grafie L istnieje droga od i do j nie przechodząca przez wierzchołek 0. Grafowi T odpowiada zero-jedynkowa macierz sąsiedztwa wierzchołków X = [x_ij]

Macierz X dla grafu T odpowiadającego cyklicznemu rozmieszczeniu maszyn L ma następujące własności:

(a) x_ij = l i x_ji = 0 lub x_ij = 0 i x_ji = 1 i ≠ j.

(b) Jeżeli x_ik, = l i x_kj = l, to x_ij = l.

Zadanie zaprojektowania optymalnego, cyklicznego rozmieszczenia maszyn można sprowadzić do następującego problemu wyznaczenia elementów x_ij macierzy X

Model M2.9

Zminimalizować (liczba pełnych okrążeń całej sieci)

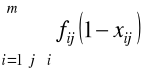
(2.61)

przy ograniczeniach (zachowanie własności (a) i (b) macierzy X)

, (2.62)

(2.64)

Rozwiązanie poszukuje się za pomocą metody podziału i ograniczeń, a także przy zastosowaniu algorytmów przybliżonych.

Typowa heurystyka

Wprowadza się względny przyrost
w wyniku przestawienia maszyn i, j

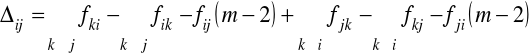
(2.67)

Jeżeli

< 0 - zamiana miejscami maszyn i oraz j jest korzystna,

> 0 - zamianę miejscami maszyn i oraz j nie należy dokonywać.

Należy wyznaczyć wartości
dla wszystkich par (i, j), i, j = l,...,m, i< j, a następnie zbudować macierz B = [b_ij]

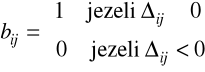
(b_ji = l - b_ij) (2.68)

Jeżeli

b_ij = l, to maszyna j może wystąpić bezpośrednio po i,

b_ij = 0 oznacza, że kolejność taka jest niekorzystna.

Macierz B traktujemy jako macierz sąsiedztwa digrafu reprezentującego dopuszczalną kolejność rozmieszczania maszyn.

Zadanie optymalizacji sprowadza się do znalezienia cyklu Hamiltona w otrzymanym grafie.

Przykład 2.3

Mamy macierz przepływów

Wyznaczamy macierz B

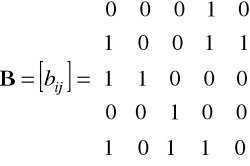
Macierzy B odpowiada cykliczny graf dopuszczalnych kolejności rozmieszczania maszyn. Zawiera on cykl Hamiltona (linią pogrubiona), będący następującą permutacją wierzchołków

 = (1,4,3,2,5)

Rys. 2.10. Graf dopuszczalnych kolejności rozmieszczania maszyn

Ocena wstępna projektu ESP

Metody oceny wstępnej:

• symulacja komputerowa

• metody analizy sieci kolejkowych.

ESP modelujemy za pomocą zamkniętej sieci kolejkowej. Zakładamy, że każdorazowo gdy jakaś gotowa część opuszcza system poprzez stanowisko wyładunkowe, na jej miejsce natychmiast jest wprowadzana poprzez stanowisko załadunkowe nowa część do obróbki.

Algorytm analizy wartości średnich

Pozwala na ujawnienie w projektowanym systemie zbędnych nadwyżek mocy produkcyjnych lub "wąskich gardeł".

W algorytmach analizy wartości średnich najczęściej przyjmuje się, że części oczekujące na obsługę są wykonywane w kolejności przybywania do danej maszyny (FIFO).

Oznaczenia:

i - indeks maszyny (lub grupy jednakowych maszyn), i = l,..., M

k - indeks typu części, k = l,..., N

L - całkowita liczba palet (części) w systemie

L_k - liczba palet dla części typu k

p_ik - średni czas wykonywania części typu k na maszynie i podczas jednego pobytu na tej maszynie

q_ik - średnia długość kolejki dla maszyny i oraz części typu k (liczba części typu k oczekujących przed maszyną oraz ewentualnie część będąca w toku obróbki)

r_ik - średni czas oczekiwania części typu k przed maszyną i

s_ik - średnia liczba pobytów każdej części typu k na maszynie i

t_ik - średni czas przebywania (oczekiwania i obróbki) części typu k przy maszynie i podczas jednego pobytu

u_i - średnie wykorzystanie maszyny i

λ_k - średnia wydajność systemu względem części typu k (liczba części typu k wytwarzanych w systemie w jednostce czasu)

λ_ik -średnia liczba części typu k wykonywanych na maszynie i w jednostce czasu

Rozpatrzmy system, w którym wytwarza się jeden typ części (indeks k pomijamy).

Jest oczywistym, że

t_i =p_i+ r_i

gdzie

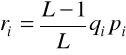
Długość kolejki q_i jest skorygowana przez czynniki (L - 1)/L. Czynnik ten uwzględnia fakt, że kolejka q_i obserwowana jest przez jedną z części nie będącą jej elementem.

Ostatecznie otrzymujemy zależność

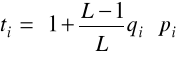
Mnożąc powyższą równość obustronnie przez s_i podstawiając T_i =s_it_i, oraz P_i =s_ip_i otrzymujemy pierwszą podstawową relację dla omawianej metody.

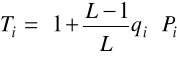
(2.70)

gdzie T_i oraz P_i oznaczają łączny średni czas przebywania części przy maszynie i oraz łączny średni czas wykonywania części na tej maszynie podczas wszystkich pobytów

Z prawa Little'a w zastosowaniu do rozważanej sieci otrzymujemy

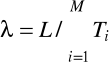
(2.71)

Zastosowanie prawa Little'a do maszyny i prowadzi do następującej zależności

(2.72)

Na podstawie tych wzorów opracowano poniższy algorytm.

Obliczenia kończy wyznaczenie wartości zmiennych u_i reprezentujących stopień wykorzystania maszyn.

Opisaną powyżej metodę analizy wartości średnich bezpośrednio uogólnia się na przypadek zamkniętej sieci kolejkowej, w której występuje wiele różnych typów części. Dla takiego przypadku powyższe wyrażenia należy zastąpić przez następujące zależności:

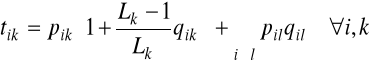
(2.73)

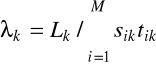
(2.75)

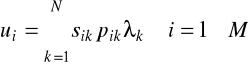
(2.76)

Dla rozważanego modelu zamkniętej sieci kolejkowej wydajność każdej maszyny i względem części typu k wynosi

(2.77)

W szczególności dla stanowiska załadunkowo-wyładunkowego (oznaczmy go przez i = l) mamy

s_1k = l,
i,

czyli

λ_ik = λ_k,
k.

Oznacza to, że wydajność systemu względem poszczególnych typów części można określić jako liczbę części tego typu przechodzących przez stanowisko wyładunkowe w jednostce czasu.

Modyfikacja modelu w przypadku, gdy indeks i oznacza grupę jednakowych maszyn o liczności m_i > l.

Czas r_ik oczekiwania części na obróbkę na maszynie z grupy i będzie w przybliżeniu m_i razy krótszy.

Prawdopodobieństwo zajętości wszystkich maszyn w grupie i można w przybliżeniu przyjąć jako równe
.

Aby uwzględnić powyższe fakty, należy drugi i trzeci składnik w wyrażeniu (2.73) pomnożyć przez następujący czynnik korekcyjny

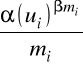
gdzie dodatkowe współczynniki korekcyjne
są dobierane eksperymentalnie dla osiągnięcia najlepszej zbieżności procedury iteracyjnej, podobnej do opisanej w Algorytmie 2.2.

23

Elastyczne systemy produkcyjne - pojęcia podstawowe .

Najważniejsze cechy ESP

• sterowanie komputerowe;

• wysoki stopień automatyzacji i integracji elementów systemu;

• różnorodność jednocześnie produkowanych części, w krótkich seriach (np. jednostkowo) i z wysoką wydajnością.

Krok 0. Przyjmij wartości początkowe q_i

q_i = L/M; i=1,...,M

Krok 1. Wyznacz kolejno wartości T_i,
oraz

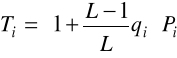
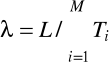
i=1,...,M

Krok 2. Jeżeli
dla każdego i (ε - zadana stała), to idź do Kroku 3. Inaczej podstaw
, i = l,..., M i wróć do Kroku 1.

Krok 3. Wyznacz u_i = P_i λ, i = l,..., M i zakończ obliczenia.

Algorytm 2.2

Krok 0. Wyznaczyć macierz zmodyfikowanych przepływów

Krok 1. W macierzy
odnaleźć największy element

Ustawić obok siebie maszyny i*, j* i włączyć tę parę do rozwiązania częściowego.

Podstawić
.

Krok 2. Wyznaczyć

Ustawić maszynę s* obok r* i dołączyć s* do rozwiązania częściowego, a następnie usunąć wiersz r* i kolumnę r* z macierzy
.

Jeżeli r* = i*, to podstawić i* = s*; inaczej j* =  s*.

Krok 3. Powtarzać Krok 2 aż do wyznaczenia pełnego rozwiązania końcowego, które zawierać będzie wszystkie maszyny.

Jedynka oznacza możliwość przejścia od wierzchołka i do wierzchołka j w grafie L bez przechodzenia przez wierzchołek 0.

Algorytm 2.1 (algorytm zmodyfikowanego drzewa rozpinającego)

1. Dobór wyposażenia sprzętowego

2. Rozmieszczenie maszyn

Projektowanie ESP
wymaga rozwiązania dwóch podstawowych zadań

Najprostszy typ ESP

Jedna obrabiarka ogólnego przeznaczenia sterowana numerycznie, która wyposażona w zmieniacze narzędzi i palet oraz bufor półfabrykatów i obrabianych detali.

Obrabiarka CNC
	Zmieniacz palet
Bufor detali

Elastyczny moduł produkcyjny

Kilka modułów produkcyjnych zintegrowanych poprzez transport, magazynowanie i wspólne sterowanie komputerowe.

Elastyczne gniazdo produkcyjne

Zbiór specjalistycznych maszyn rozmieszczonych w ustalonym porządku, w którym każda operacja może być wykonywana na jednej tylko maszynie.

Różni się od automatycznej linii produkcyjnej zdolnością do częstych i szybkich przezbrojeń.

Elastyczna linia produkcyjna

Kilka wzajemnie powiązanych linii, gniazd lub pojedynczych modułów.

Elastyczna sieć produkcyjna

Elastyczność

Zdolność systemu do jednoczesnej krótko­seryjnej (w tym jednostkowej) produkcji wielu różnych typów części, przy wysokiej wydajności systemu

Podatność systemu na przeprowadzanie zmian niezbędnych przy produkcji danej rodziny typów części

(miara - czas wymiany zużytego lub uszkodzonego narzędzia, czas wymiany narzędzi w magazynku na obrabiarce przy przejściu do produkcji innego podzbioru danej rodziny typów części, czas przygotowania produkcji na danej obrabiarce, itp.)

Elastyczność maszyn

Zdolność do szybkiego i ekonomicznego przejścia do produkcji nowego typu wyrobów

(miara - czas konieczny do przejścia od produkcji jednej rodziny typów części do innej).

Elastyczność asortymentu produkcji

Zdolność systemu do rentownej produkcji przy różnych jej wielkościach.

(miara - najmniejsza wielkość produkcji dla wszystkich typów części, przy której system jest jeszcze rentowny).

Elastyczność wielkości produkcji

Zdolność do produkowania danego zbioru typów części różnymi sposobami i przy użyciu różnych materiałów.

(miara - liczba typów części, które mogą być jednocześnie wytwarzane w sposób jednostkowy).

Elastyczność procesu technolo­gicznego

Zdolność systemu do kontynuowania produkcji danego zbioru typów części w warunkach występowania awarii.

Marszruta - ciąg maszyn, przez które przechodzi kolejno dany typ części w procesie wytwórczym.

Rozróżniamy elastyczności marszrut:

• potencjalną - marszruty są z góry ustalone, a w przypadku awarii są one automatycznie korygowane;

• faktyczną - części tego samego typu są wytwarzane przy różnych marszrutach niezależnie od sytuacji awaryjnych.

Elastyczność marszrut osiąga się poprzez automatyzację korekt marszrut, agregowanie maszyn w grupy lub dublowanie przydziałów operacji do maszyn. Przyjmuje się następującą miarę elastyczności marszrut

EM = - 1

Dodatnia wartość EM wskazuje na możliwość wykorzystania alternatywnych marszrut przepływu części przez system.

Dodatkową do EM miarą elastyczności systemu przyjmuje się wskaźnik

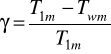
gdzie:

T_1m - czas realizacji zamówienia w przypadku jednej ustalonej marszruty dla każdego typu części (EM = 0);

T_wm - czas realizacji zamówienia w przypadku wykorzystania wielu alternatywnych marszrut dla każdego typu części (EM > 0).

Elastyczność marszrut technolo­gicznych

liczba wszystkich marszrut

liczba typów części

Zdolność systemu do łatwej i modularnej rozbudowy i rozwoju.

Elastyczność rozwoju osiąga się poprzez:

• stosowanie elastycznego systemu transportu;

• stosowanie modularnych, elastycznych gniazd obróbkowych ze zmieniaczami palet;

• elastyczność marszrut technologicznych.

Elastyczność rozwoju systemu

Zdolność do zmiany kolejności wykonywania pewnych operacji dla każdego typu części.

Decyzje te podejmuje się w czasie rzeczywistym w zależności od aktualnego stanu systemu.

Elastyczność ograniczeń kolejnościo­wych

Zdolność do prowadzenia procesu produkcyjnego ze zmienną liczbą operatorów.

Elastyczność wielkości personelu

Określa ogół typów części, które ESP może produkować.

Jest tym wyższa, im nowocześniejsza jest zastosowana technologia oraz im większa jest uniwersalność obrabiarek.

Wymagane są wszystkie dotychczas wymienione typy elastyczności.

Elastyczność produkcji

• elastyczność na poziomie maszyny;

• elastyczność na poziomie zarządzania systemem.

---