WYKŁAD VIII

Opory ruchu i rozkład prędkości przy jednostajnym ruchu laminarnym

Przepływ w prostym przewodzie o przekroju kołowym.

W przewodzie o promieniu
wyodrębniliśmy powierzchnię walcową o promieniu r współśrodkową z osią przewodu (rys. 37). Odległość od wyodrębnionej powierzchni do ścianki przewodu oznaczmy przez y. Zatem y=ro-r lub
. Przy ruchu laminarnym, wobec tego, że cząstki cieczy poruszają się równolegle do osi przewodu i nie ma ruchów poprzecznych, opory ruchu powstają tylko dzięki lepkości i zwią­zanym z nią naprężeniom stycznym do kierunku ruchu. Opory powstające przy ruchu wyodrębnionego myślowo walca cieczy możemy wyrazić przez styczne na­prężenia
na jego powierzchni.

Rys. 37

Podobnie jak poprzednio, biorąc pod uwagę ciśnienia panujące na końcach odcinka L w obszarze naszego wyodrębnionego walca, możemy

lub

albo rozpatrując nieskończenie mały odcinek przewodu dL

Porównując tę zależność z zależnością dotyczącą całego przekroju
otrzymamy zależność

Opierając się na równaniu (1)możemy wyrazić naprężenie
a pomocą wzoru:

zatem

skąd

Zgodnie z przyjętym poprzednio założeniem, przy ściance przewodu, to znaczy przy
prędkość
, zatem prędkość w dowolnym punkcie przekroju odległym o r od osi przewodu możemy wyrazić w postaci całki:

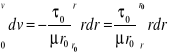
a po scałkowaniu

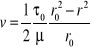
(34)

Równanie (34) wyraża rozkład prędkości w przekroju przewodu kołowego przy ruchu laminarnym (rys. 38). Jest to równanie paraboloidy obrotowej. Jak łatwo zauważyć, maksymalna prędkość panuje na osi rury, to znaczy przy r=0 i równa się

Wydatek Q równa się objętości paraboloidy pręd­kości, skąd łatwo dochodzimy do wniosku, że średnia prędkość w przekroju równa się połowie prędkości maksymalnej, a więc

Skąd

Porównując to wyrażenie z wyrażeniem (32), przy którym również mieliśmy na myśli średnią prędkość w przekroju, otrzymamy zależność

Wynika stąd, że współczynnik oporu równa się :

Przypomnijmy, że
, czyli w danym przypadku przy ruchu laminarnym mamy

Skąd wynikają wartości n==l. C' ==16.

Podstawiając otrzymaną wartość A do wzoru (33) otrzymamy wartość straty na długości przewodu w przypadku ruchu laminarnego

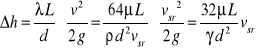
Widzimy teraz, że przy ruchu laminarnym otrzymujemy straty na długości przewodu proporcjonalne do prędkości w pierwszej potędze, czyli zależność, którą otrzymujemy doświadczalnie, jak już mówiliśmy poprzednio.

Przepływ w szerokim prostym korycie otwartym o przekroju prostokątnym.

Dla uproszczenia rozpatrywanego zjawiska przyjmujemy, że szerokość koryta jest na tyle duża, że opory wywołane wpływem bocznych ścianek pionowych możemy pominąć. Przy tym założeniu możemy zagadnienie rozpatrywać tak, jakbyśmy wyodrębnili z nieskończenie szerokiego koryta pas o szerokości równej jedności.

Rys. 39

Jeżeli w prostym korycie o stałym przekroju panuje ruch jednostajny, to znaczy, że wszystkie przekroje poprzeczne strumienia cieczy są sobie równe, a prędkości w odpowiadających sobie punktach, a więc i prędkości średnie w przekrojach, są jednakowe, bo swobodne zwierciadło cieczy układa się równolegle do dna koryta. Jeżeli ponadto przyjmiemy, że na całej powierzchni swobodnego zwierciadła cieczy panuje jednakowe ciśnienie, dajmy na to atmosferyczne, to dochodzimy do wniosku, że piezometryczna linia ciśnień pokrywa się z linią zwierciadła w przekroju po­dłużnym.

Rozpatrzmy ruch na odcinku o długości L przy przyjętych założeniach (rys. 9). Będziemy przy tym traktować, iż pochylenie dna w stosunku do poziomu jest na tyle małe, że przekroje pionowe możemy traktować jako prostopadłe do kierunku ruchu. Wyodrębnijmy pas o grubości z ograniczony od góry płaszczyzną swobod­nego zwierciadła, od dołu płaszczyzną do niej równoległą (zakreskowany na rysunku).

Przy przyjętych założeniach, prędkości i ciśnienia w odpowiadających sobie punktach przekrojów 7 i 2 są równe. Wynika stąd, że strata energii na odcinku L wyrażona spadem linii ciśnienia
(linia energii jest równoległa do linii ciśnień) spowodowana jest tylko oporami na dolnej powierzchni wyodrębnionego pasa, a wobec założenia ruchu laminarnego opory te wywołane są tylko lepkością cieczy.

Oznaczmy naprężenia styczne (przypadające na jednostkę powierzchni) na dolnej powierzchni wyodrębnionego pasa przez
. Opory na powierzchni swobod­nego zwierciadła wynikające na skutek zetknięcia się cieczy z otaczającym środo­wiskiem (np. powietrzem) pomijamy. Dla uchwycenia zależności między spadem linii ciśnień Ah a naprężeniami
rozpatrzmy pracę sił ciążenia i sił lepkości przy przesunięciu wyodrębnionego pasa cieczy o ds (rys. 39).

Pracę siły ciążenia określa wyrażenie:

Pracę sił lepkości — wyrażenie:
. Stąd otrzymujemy zależność

lub

lecz zgodnie ze wzorem (l)

Uwzględniając podane zależności dochodzimy do równania

lub po scałkowaniu

dla wyznaczenia stałej całkowania przypomnijmy założenie, że cząstki przylegające bezpośrednio do ścianki stałej są w spoczynku. Inaczej mówiąc, że przy z=h, v=0, skąd

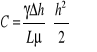
a zatem

jest to równanie paraboli, a prędkość osiąga maksimum przy z=0, przy czym

Jeżeli przez I oznaczymy spadek linii ciśnień, to w danym przypadku również spadek zwierciadła
Rozkład prędkości pokazany jest na rys. 40.

Znając rozkład prędkości w przekroju możemy określić prędkość średnią, a mianowicie

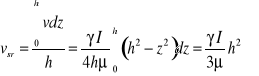
Uwzględniając wyrażenia (35) i (37) oraz oznaczając przez
naprężenie tnące przy dnie, czyli przy z=h, otrzymujemy wartość

a przy porównaniu otrzymanej wartości z równaniem (32), pamiętając, że w rów­naniu (32) mieliśmy na myśli prędkość średnią, mamy

skąd

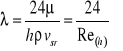
(38)

Przypominamy, że przy określeniu liczby Reynoldsa

zastrzegliśmy, że jako / możemy przyjmować

dowolnie obrany odcinek długości. W danym przypadku przyjęliśmy głębokość h, co zostało zaznaczone doda­niem znaczka (h) przy symbolu Re.

Otrzymane wyniki wskazują, że podobnie jak w prze­wodach kołowych, przy ruchu laminarnym straty są proporcjonalne do prędkości w pierwszej potędze, a wykładnik potęgi przy liczbie Reynoldsa w wyrażeniu określającym współczynnik oporu A równa się n=1.

Wartości współczynnika Saint-Venanta.

Po zapoznaniu się z rozkładami pręd­kości w przekrojach poprzecznych możemy rozpatrzyć wartości współczynnika Saint-Venanta (Coriolisa) wprowadzony do równania Bernoulliego (30). Dokładnie poznaliśmy rozkłady prędkości w przypadku ruchu laminarnego w rurze o prze­kroju kołowym oraz w szerokim prostokątnym korycie, dla tych dwóch przypad­ków możemy obliczyć wartość
.

Przy ruchu laminarnym w przekroju kołowym rozkład prędkości wyraża wzór (34), a mianowicie:

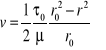
średnia zaś prędkość

Możemy zatem wyrazić rozkład prędkości w zależności od prędkości średniej

Współczynnik Saint Venanta (Coriolisa)
określony jest wzorem:

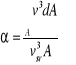
Ze względu na symetryczny rozkład prędkości w stosunku do osi rury jako elemen­tarne poletko d A możemy przyjąć pierścień o promieniu r i szerokości dr, czyli
. Pole przekroju
.

Podstawiając podane wartości do wzoru na a otrzymamy

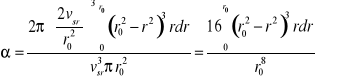
lecz

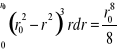
zatem;

Przy ruchu laminarnym w szerokim korycie prostokątnym rozkład prędkości w pio­nie wyrażony jest wzorem (36)

skąd

Mamy na myśli na tyle szerokie koryto, że wpływ ścianek bocznych możemy po­minąć, a zatem możemy rozpatrywać wycięty przekrój o szerokości jednostkowej. Wobec tego A =1 h oraz dA=ldz.

Podstawiając te wartości do wzoru (30) otrzymujemy

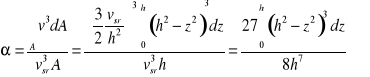
lecz

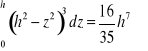
zatem

W przypadkach gdy znany jest nam rozkład prędkości w przekroju, lecz nie jest wyrażony w postaci pewnej zależności algebraicznej, ale za pomocą wartości w wielu punktach pomiarowych lub w postaci wykreślonych linii jednakowych prędkości, dla przybliżonego obliczenia a, możemy we wzorze (30) całkowanie zastąpić sumą iloczynów skończonych, a mianowicie

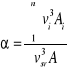
Gdzie
pola dostatecznie małych pól, na które podzieliliśmy przekrój tak, aby móc przyjąć, że w obszarze każdego z tych pól panuje stała prędkość,
— pręd­kości odpowiadające polom
.

Opory ruchu i rozkład prędkości przy jednostajnym ruchu burzliwym

Jak wiemy z doświadczeń Reynoldsa, na podstawie których ustaliliśmy podział rodzajów ruchu na laminarny i burzliwy, ruch burzliwy charakteryzuje się róźno-kierunkowym ruchem cząstek. W tym na pozór zupełnie chaotycznym ruchu mo­żemy jednak wyróżnić kierunek główny i odpowiednią przeciętną prędkość w tym kierunku z tym, że dodatkowe ruchy traktujemy jako ruchy pulsacyjne. Przyjmijmy kierunek ruchu głównego za oś x. Mówiąc o prędkościach chwilowych możemy powiedzieć, że chwilowa prędkość w kierunku ruchu głównego

a .prędkości w kierunku osi y i z prostopadłych do kierunku głównego będą odpowiednio:

Prędkości
są to prędkości pulsacji zmienne co do wartości i znaku. W dal­szych rozważaniach, dla uproszczenia będziemy traktowali ruch jako płaski, to znaczy przyjmiemy
. Nie umniejszy to ogólności naszych rozważań. Zja­wisko ruchu burzliwego jest zjawiskiem bardzo złożonym i trudnym do ścisłego ujęcia, toteż dotychczas brak jest ścisłej teorii tego ruchu. Dla zapoznania się ze sposobami podejścia do ruchu burzliwego rozpatrzymy w ogólnych zarysach teorię Prandtla.

Rozpatrzmy pewien punkt, w którym panuje przeciętna prędkość
. W oto­czeniu tego punktu wyodrębniliśmy myślowo nieskończenie małe poletko
po­łożone równolegle do głównego kierunku ruchu i prostopadle do osi y. Gdyby nie było chwilowych ruchów bocznych, to znaczy gdyby nie było pulsacji, przepływ przez powierzchnię obranego poletka równałby się zeru. Jednak na skutek istnienia prędkości pulsacji istnieje chwilowy przepływ przez powierzchnię naszego poletka i w ciągu nieskończenie krótkiego czasu
przez poletko przepływa elementarna masa cieczy

Zaznaczyliśmy tu bezwzględną wartość chwilowej prędkości pulsacji
dlatego, że prędkość ta może

mieć różne znaki, a masa jest wartością dodatnią,

Przyjmijmy, że prędkości pulsacji
i
dotyczą rozpatrywanej cząstki, nie dotyczą zaś cząstek sąsiednich tak jakby w otoczeniu rozpatrywanej cząstki pręd­kości pulsacji były równe zeru. Schemat ten nie umniejsza ogólności rozumowania, zawsze bowiem wartość
możemy traktować jako różnicę prędkości pulsacji naszej cząstki i cząstek w warstwie sąsiedniej. Jeżeli więc masa
, która ma w danej chwili prędkość pulsacji
, po przejściu przez poletko zostanie jej pozbawiona, to znaczy, że nastąpi zmiana pędu o wartość

Zmiana pędu w kierunku osi x musiała być spowodowana pewną siłą AF działającą w tym kierunku (to znaczy stycznie do głównego kierunku ruchu). W oparciu o za­sadę pędu i popędu możemy zatem napisać

lub

Dzieląc obie strony równania przez
otrzymamy wartość dodatkowego naprę­żenia stycznego do głównego kierunku ruchu wywołanego istnieniem pulsacji, a mianowicie:

(39)

Znak minus postawiony jest dlatego, że naprężenie ścinające
traktujemy jako dodatnie (podobnie jak umówiliśmy się przy wzorze l), natomiast iloczyn

z natury rzeczy jest ujemny. Możemy to wyjaśnić, jeżeli zwrócimy uwagę, że pręd­kościom pulsacji towarzyszy odkształcenie rozpatrywanej cząstki cieczy, jeżeli przyjmiemy np., że (pomijając ściśliwość przy zachowaniu ciągłości) dodatniej prędkości
towarzyszy wydłużenie cząstki w tym kierunku (rozciągnięcie cząst­ki), to równocześnie następuje jej zwężenie w kierunku poprzecznym, to znaczy, że
ma znak ujemny. Rozumowanie to wskazuje, że panujące równocześnie pręd­kości
i
zawsze mają znaki przeciwne, a ich iloczyn jest zawsze ujemny. Zwróćmy jeszcze uwagę, że o ile przeciętne wartości prędkości pulsacji w każdym kierunku są równe zeru: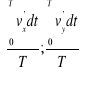
, to przeciętna wartość iloczynu

by­najmniej nie równa się zeru.

Wyznaczone przed chwilą dodatkowe naprężenie styczne wywołane pulsacją występuje niezależnie od rozpatrywanych poprzednio naprężeń stycznych powsta­jących dzięki lepkości cieczy, a zatem całkowite naprężenie styczne występujące przy pulsacyjnym ruchu cieczy lepkiej równa się

(40)

Aby przejść od uzależnienia naprężeń
od prędkości pulsacji do uzależnienia od prędkości przeciętnej, Prandtl przyjmuje, że składowe prędkości pulsacji są pro­porcjonalne do przyrostu przeciętnej prędkości przy poprzecznym przesunięciu się cząstki o pewną wartość
. Pamiętając, że wartości
i
mają odmienne znaki możemy napisać

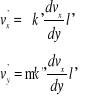
Iloczyn składowych prędkości pulsacji wyrazi się wówczas w postaci:

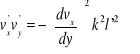
lub

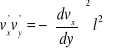
gdzie wartość l wyraża przesunięcie z uwzględnieniem współczynnika proporcjonal­ności.

Podstawiając to wyrażenie do wzoru (40) otrzymamy

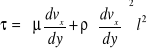
(41)

Przy ruchu laminarnym nie mamy do czynienia z przesunięciami poprzecznymi cząstek (w stosunku do głównego kierunku ruchu), czyli że w tym przypadku
, a naprężenia styczne są proporcjonalne do prędkości średniej w pierwszej potędze.

Przy silnie rozwiniętej burzliwości drugi wyraz prawej strony równania (41) staje się na tyle duży w porównaniu z pierwszym, że pierwszy wyraz możemy po­minąć (z wyjątkiem warstewki przyściennej). Możemy więc przyjąć, że

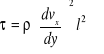
(41')

to znaczy, że naprężenia
stają się proporcjonalne do kwadratu prędkości średniej. Mówimy wówczas, że mamy do czynienia z obszarem „kwadratowego prawa oporu".

Wreszcie w przypadkach przejściowych, gdy obydwa wyrazy prawej strony równania (41) mają podobny rząd wielkości, opory stają się proporcjonalne do prędkości średniej w potędze nieco niższej od 2.

Doświadczenia potwierdzają na ogół wnioski wysnuwane w oparciu o równa­nie (41), można przeto uważać, że przyjęte założenia są w zasadzie słuszne.

Równanie (4l') możemy przedstawić w następującej postaci

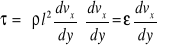
wówczas wartość
przedstawia tak jakby współczynnik ,,burzliwej" lepkości. Nie­kiedy nazywa się go współczynnikiem burzliwej wymiany.

Należy jednak podkreślić zasadniczą różnicę między
i
, gdyż
dla określonej cieczy przy danej temperaturze jest stałe, wówczas gdy
zmienia się w zależności od położenia punktu w przekroju i jest własnością ruchu cieczy, a nie samej cieczy.

Rozkład prędkości przeciętnych przy ruchu burzliwym, dzięki istnieniu po­przecznych prędkości pulsacji i mieszaniu się cząstek różnych warstw, ma charakter bardziej wyrównany niż w przypadku ruchu laminarnego. Ponieważ opory, a więc i rozkład prędkości, zależy jak wynika ze wzoru (41 lub 41') od trudnej do doświad­czalnego ustalenia wartości l, to wzory ujmujące rozkład prędkości opierają się na dowolnie założonych rozkładach, l. Z tych względów ograniczymy się jedynie do opisowego omówienia rozkładu prędkości w przekroju poprzecznym przy ruchu burzliwym. Przede wszystkim należy zwrócić baczną uwagę na specyficzne warunki ruchu tuż przy ściankach przewodu lub koryta. Z jednej strony ścianki nie pozwa­lają na istnienie prędkości pulsacji w kierunku do nich prostopadłym w warstwie cieczy przylegającej do ścianek, z drugiej strony, jak to mówiliśmy już przedtem, cząstki cieczy bezpośrednio przylegające do ścianek są przez nie hamowane i znaj­dują się w spoczynku, a w bezpośrednim otoczeniu ruch jest powolny. Wymienione warunki powodują, że w warstewce cieczy przylegającej do ścianek panuje ruch laminarny, dopiero w pewnym oddaleniu od ścianek mogą powstawać pulsacje poprzeczne, a co za tym idzie ruch burzliwy. Tę warstewkę ruchu laminarnego

nazywamy warstewką przyścienną. Grubość warstewki przyściennej bywa niekiedy bardzo mała wyrażająca się w ułamkach milimetra, jednak warstewka przyścienna gra dużą rolę w kształtowaniu się ruchu burzliwego. Nawet przy ściankach dosko­nale gładkich warstewka przyhamowana przez ścianki jest źródłem zaburzeń w dal­szych warstwach strumienia, a tym samym przyczynia się do powstawania burzliwości. Według fenomenologicznej teorii Broszki działanie warstewki przyściennej polega na tym, że w warstewce tej dzięki wpływowi ścianki ciecz nabiera odmien­nych własności mechanicznych w porównaniu do pozostałej cieczy. Dlatego zew­nętrzną powierzchnię warstewki przyściennej można traktować jako rozgraniczenie między różnymi cieczami. Możemy to porównać z powierzchnią zwierciadła wody w rzece lub jeziorze i przylegającym do niej powietrzem. Przy ruchu powietrza na skutek przypadkowych różnic w ciśnieniach powstaje na powierzchni ruch falowy. Podobnie ruch falowy warstewki przyściennej wpływa na zaburzenia w po­zostałych warstwach cieczy.

Na zaburzenia ruchu wpływa również szorstkość ścianek inaczej mówiąc drobne występy na ściankach. Przy przeprowadzeniu doświadczeń, jak zobaczymy dalej, wyraźnie daje się zauważyć wpływ szorstkości ścianek. Jednak w wielu przypadkach przy mniejszych prędkościach średnich przewody zachowują się tak samo jak prze­wody zupełnie gładkie, a wpływ szorstkości zaczyna się uwidaczniać dopiero przy większych prędkościach. Zjawisko to daje się również wytłumaczyć istnieniem warstewki przyściennej. Chodzi ó to, że w miarę wzrostu prędkości maleje grubość warstewki przyściennej. Otóż dopóki warstewka przyścienna jest na tyle gruba, że pokrywa wszystkie występy ścianki, przewód zachowuje się tak jak przewód gładki, dopiero gdy występy nie są pokryte warstewką przyścienną, mają bezpo­średni wpływ na stopień burzliwości.

Jeżeli chodzi o rozkład prędkości, to w obrębie bardzo cienkiej warstewki przy­ściennej prędkości rosną bardzo szybko według prawa rozkładu przy ruchu laminarnym. Poza warstewką przyścienną panuje jeszcze duży przyrost prędkości, gradient prędkości, który dzięki burzliwości ruchu szybko maleje w miarę oddalania się od ścianki i w dalszym ciągu mamy do czynienia z bardziej równomiernym rozkładem prędkości. Charakter rozkładu prędkości w przekroju poprzecznym przewodu o przekroju kołowym pokazany jest na rys. 41, w korycie otwartym na rys, 42.

Obliczyliśmy, że przy ruchu laminarnym w przypadku rury okrągłej współ­czynnik Saint-Yenanta
, w przypadku szerokiego koryta prostokątnego
. Wartość
jest tym większa, im bardziej nierównomierny jest rozkład prędkości w przekroju. Jak łatwo zauważyć, ze wzoru (30) przy zupełnie równo­miernym rozkładzie prędkości w przekroju, czyli przy
,
. Im bardziej równomierny jest rozkład prędkości w przekroju, tym a staje się bliższe jedności.

Jak wiemy, w przypadku ruchu burzliwego następuje wyrównanie prędkości w przekroju poprzecznym. W rurach o przekroju kołowym wyrównanie jest tak znaczne, że z dostateczną dla praktyki dokładnością możemy przyjmować
. W kanałach i naturalnych korytach otwartych w przypadkach najczęściej spoty­kanych w praktyce możemy przyjmować wartość
. Są to oczywiście orienta­cyjne wartości przybliżone, które możemy stosować nie mając bliższych wiadomości o rozkładzie prędkości opartym chociażby na bezpośrednich pomiarach w każdym poszczególnym przypadku.

§ 23. Opory ruchu ciał poruszających się w cieczy

Rozpatrzmy od jakich czynników może zależeć siła oporu jaką stawia ciało o danym kształcie poruszające się ruchem jednostajnym w cieczy. Mamy tu do czynienia z bryłą o wielkości scharakteryzowanej pewnym wymiarem /, poruszają­cej się z prędkością v w ośrodku o lepkości
i gęstości
. Są to wszystkie elementy określające jednoznacznie zjawisko, a więc mogące mieć wpływ na wielkość opo­ru R.

Dysponujemy zbiorem elementów wymiarowych
, których miana można utworzyć z trzech mian podstawowych — długości, masy i czasu. Zgodnie z twierdzeniami analizy wymiarowej pełna seria dla tego zagadnienia zawiera 2 iloczyny bezwymiarowe, np.

Szukane wyrażenie ma więc postać:

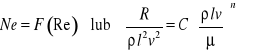
Liczby C \n nie mogą być już wyznaczone na drodze analizy wymiarów i wymagają znajomości istoty zjawiska, bądź przynajmniej pewnej ilości obserwacji.

Podobnie jak przepływy w przewodach i korytach, tak i opływy brył mogą być laminarne i burzliwe, przy czym nie ma istotnej różnicy w samym mechanizmie wewnętrznego tarcia cieczy między przepływami w przewodach a opływami. Prze­analizujemy dalej wzór jedynie dla przypadków skrajnych to znaczy ruchu laminarnego i w pełni burzliwego.

Wzór na opór przedstawia się następująco:

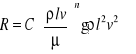
Wiemy z doświadczeń, że w ruchu laminarnym opory ruchu są proporcjonalne do prędkości w pierwszej potędze. We wzorze v występuje z wykładnikiem n 4-2, stąd
.

Wobec tego:

Współczynnik C zależy od elementu przyjętego w rozważaniach jako dany, to znaczy kształtu ciała, przy czym należy tu rozumieć nie tylko wzajemne pro­porcje wymiarów bryły, ale również jej zorientowanie względem kierunku prędkości.

Dla kuli o średnicy d opór przy oplywie laminarnym wynosi:

Wzór ten uzyskał w r. 1851, na drodze analizy równań ruchu, G. G. Stokes. Ma on zastosowanie przy badaniu opadania drobnych zawiesin gruntu w wodzie, lub kropelek mgły, o średnicy mniejszej niż 0,01 mm, w .powietrzu.

W ruchu w pełni burzliwym obowiązuje „kwadratowe prawo oporów" ruchu. Zależność ta może być spełniona tylko dla n=0, a więc w ruchu w pełni burzliwym

C zależy podobnie jak dla ruchu laminarnego, od kształtu i ustawienia ciała.

Jeżeli wprowadzimy drobne zmiany w sposobie zapisu wzorów na opory w ruchu laminarnym i burzliwym, otrzymamy

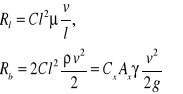
Jak widać z powyższych równań, w ruchu laminarnym decydują naprężenia styczne, dv

zgodnie z wzorem Newtona
, natomiast w ruchu burzliwym — parcie dn hydrodynamiczne.

Wzór na opór w ruchu burzliwym podawany jest najczęściej w ostatniej z wy­mienionych postaci, przy czym
oznacza pole rzutu bryły na płaszczyznę prosto­padłą do kierunku prędkości czyli tzw. przekrój czołowy.

8

1

---