1.Działanie na wektorach i skalarach
dodawanie
odejmowanie
rozkład wektora na składowe
mnożenie wektora przez liczbe
Mnożenie wektora przez liczbę daje wektor
mnożenie wektorów
2. Podstawowe wielkości charakteryzujące ruch postępowy punktu materialnego
Punkt materialny: ciało obdarzone masą ,nie posiadające objętości
Prędkość punktu materialnego : chwilowa i średnia
Przemieszczenie - najkrótsza droga
Wektor przemieszczenia Δr jest to różnica pomiędzy wektorem położenia końcowego r i wektorem położenia początkowego ro
![]()
Ruch jednostajny (wartość prędkości pozostaje stała) prostoliniowy
Przyspieszenie - wielkość wektorowa, która informuje o szybkości zmian w czasie
Ruch jednostajnie zmienny
a)Ruch jednostajnie przyspieszony bez prędkości początkowej
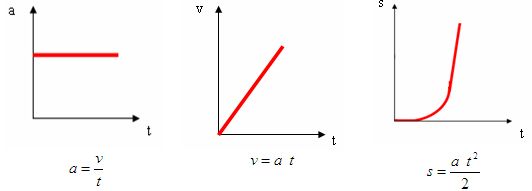
b)Ruch jednostajnie przyspieszony z prędkością początkową
c) Ruch jednostajnie opóźniony
3. Dynamika
Ciężarem ciała nazywamy siłę grawitacyjną z jaką Ziemia przyciąga to ciało.
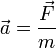
I zasada dynamiki(bezwładności)-Jeżeli na ciało nie działa żadna siła wypadkowa to ciało pozostaje w spoczynku, albo porusza się ruchem jednostajnym prostoliniowym
II zasada dynamiki- Wypadkowa siła działająca na ciało jest proporcjonalna do masy ciała i przyspieszenia.
III zasada dynamiki- Siła akcji i reakcji zawsze występują parami. Każdej akcji towarzyszy równa co do wartości, lecz przeciwnie skierowana reakcja. Nigdy się nie równoważą bo mają różne pkt przyłożenia.
4.Ruch po okręgu:
Cechy charakterystyczne ,definiujące ruch to :
Tor ruchu - okrąg
Ruch po okręgu może być:
Jednostajny - wartość prędkości pozostaje stała;
Niejednostajny (zmienny)- wartość prędkości zmienia się
Przyspieszenie w ruchu po okręgu nie może wynosić 0 m/s2
Z ruchem po okręgu wiążą się:
Prędkość kątowa
nazywamy stosunek zakreślonego skierowanego kąta do czasu w jakim nastąpił.
Prędkość liniowa
Przyspieszenie kątowe
jest to zmiana prędkości kątowej w czasie trwania tej zmiany.
Siła dośrodkowa
Przyspieszenie dośrodkowe
Okres T
jest to czas trwania jednego, pełnego obiegu
Częstotliwość
jest to odwrotność okresu ,a dokładnie stosunek liczby obrotów do czasu ich wykonania
5.Nieinercjalny układ odniesienia I siła Bezwładności
- układ odniesienia poruszający się ruchem niejednostajnym względem jakiegokolwiek inercjalnego układu odniesienia.
Siła bezwładności (siła inercji, siła pozorna) - siła pojawiająca się w nieinercjalnym układzie odniesienia, będąca wynikiem przyspieszenia tego układu
gdzie:
- siła bezwładności ,
- przyśpieszenie układu , m - masa ciała
Rodzaje sił bezwładności:
* siła Coriolisa - Dla obserwatora znajdującego się w obracającym się układzie odniesienia tor ruchu ciał znajdującego się w tym samym układzie jest zakrzywiony.
* siła odśrodkowa
* transwersalna siła bezwładności
6.Praca, moc , energia
Moc
Moc jest to stosunek pracy do czasu w jakim została wykonana: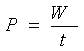
|
|
|
|
1 wat (W) jest to moc urządzenia które wykonuje pracę 1 dżula(J) w czasie 1 sekundy(s). |
|
Praca
Praca jest to iloczyn skalarny wektora siły F oraz wektora przesunięcia s:
W=F·S 1 dżul (1J) jest to praca siły 1 niutona na drodze 1 metra
Energią nazywamy zdolność układu do wykonywania pracy.
Rozróżniamy energię mechaniczną, cieplną, elektryczną, jądrową.
Energię mechaniczną dzielimy na energię potencjalną (wysokości) i kinetyczną (ruchu).
Energia potencjalna
Ep = m·g·h Ep- energia potencjalna(J) m - masa (kg) g - przyspieszenie ziemskie 9,81 m/s²
Energia kinetyczna
Ek = ½ m·v² Ek- energia kinetyczna(J) m - masa (kg) v - prędkość (m/s)
![]()
7.Pęd i zasada zachowania pędu
Pęd definiujemy jako iloczyn masy i prędkości ciała.
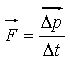
Pęd jest wektorem o zwrocie zgodnym z kierunkiem ruchu ciała. Pęd, a raczej jego zmiana , ma ścisły związek z siłą działającą na ciało.
Zasada zachowania pędu:
suma wektorowa pędów wszystkich elementów układu izolowanego pozostaje stała
Przykłady odrzutu:
* napęd odrzutowy w samolotach odrzutowych i rakietach (pęd strumienia gazów wyrzucanych z dyszy nadaje samolotowi lub rakiecie pęd w kierunku przeciwnym)
* odrzut i podrzut broni palnej
* odrzut jądra atomowego przy emisji cząstek z jądra
* sposób poruszania się niektórych zwierząt wodnych (np. meduzy)
* prysznic, gdy ustawiony zostanie na silny strumień wody, doznaje odrzutu i potrafi sam się unosić w powietrzu.
* nadmuchany otwarty balon, gdy zostanie uwolniony, doznaje odrzutu i porusza się do czasu, aż powietrze w balonie osiągnie wartość ciśnienia atmosferycznego
Przykładami zderzeń są:
* uderzenie jednej kuli bilardowej o drugą,
* pochłonięcie neutronu przez jądro uranu i następujący w wyniku tego rozpad jądra, z emisją fragmentów jądrowych i kolejnych neutronów,
* przejście komety nie związanej grawitacyjnie z układem słonecznym w okolicy Słońca, z odchyleniem jej toru spowodowanym oddziaływaniem grawitacyjnym.
8. ZASADA ZACHOWANIA ENERGII MECHANICZNEJ:
![]()
Jeśli na układ ciał nie działają siły zewnętrzne, więc jest to układ izolowany, to energia mechaniczna czyli suma energii potencjalnej i kinetycznej tego układu jest stała.
9.Wielkości charakteryzujące pole grawitacji:
Wektorowe(Siła, natężenie pola)
Skalarne(m,
,ν[potencjał],W,energia)
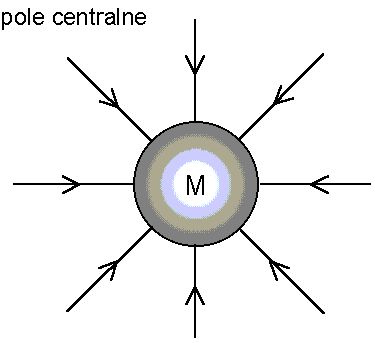
Linie sił pola: tor, po którym porusza się ciało próbne umieszczone w polu.
Natężenie pola grawitacyjnego- siła grawitacyjna w danym pkt na jednostkę masy umieszczona w polu.
![]()
m - masa ciała;
F - siła jaka działa na ciało.
![]()
MZ i RZ są odpowiednio masą i promieniem Ziemi.
![]()
Jednostka natężenia pola grawitacyjnego:
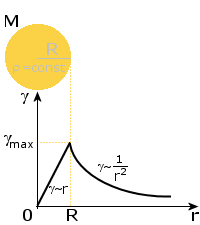
Natężenie wewnątrz pola:
r- promień
G- stała grawitacyjna
Od źródła rośnie liniowo;
Od powierzchni źródła maleje
Potencjał pola grawitacyjnego (potencjał grawitacyjny) w danym punkcie jest to stosunek energii potencjalnej ciała umieszczonego w tym punkcie pola do jego masy.
Potencjał grawitacyjny w danym punkcie pola jest równy liczbowo pracy wykonanej przy przeniesieniu ciała o jednostkowej masie z nieskończoności do tego punktu pola.
ν=
gdzie G jest stałą grawitacyjną.
Pole grawitacyjne jest wtedy centralne.
ν=-
W=
10. PRAWO POWSZECHNEJ GRAWITACJI:
![]()
Siła oddziaływania grawitacyjnego między dwoma ciałami jest wprost proporcjonalna do iloczynu tych mas
i odwrotnie proporcjonalna do kwadratu odległości między nimi:
G - stała grawitacji, m1 - masa ciała 1, m2 - masa ciała 2, r - odległość między ciałami.
11. PRAWA KEPLERA:
I. Prawo orbit - wszystkie planety poruszają się po orbitach eliptycznych, w których w jednym z ognisk znajduje się słońce.
II. Prawo pól - promień wodzący planety zakreśla w równych czasach równe pola.
III. Prawo okresów - kwadraty obiegu planet dookoła słońca są wprost proporcjonalne do sześcianów ich wielkości półosi.
T2 = Ca3 - dla elipsy Ca - stała proporcjonalności
T2 = CR3 - dla okręgu
12.RUCH CIAŁ W POLU GRAWITACYJNYM
a)rzut (ruch w polu grawitacyjnym z prędkością początkową v0=! 0)
-pionowy do góry/ na dół α=90o;
v=v0-gt
H=v0*t - -
, gdzie t=twznoszenia
HMAX=v0*
-
=
-poziomy= ruch jednostajny w kierunku poziomym + spadek swobodny; α=0o;
vp=g*t (vp-prędkość pionowa)
Z= v0*t = v0*
(Z- zasięg) H=
=> t =
-ukośny 0o<α<90o;
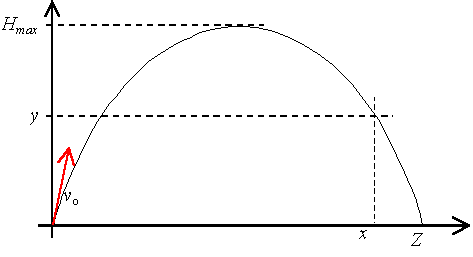
y
Hmax
x
do Hmax-rzut ukośny= ruch jednostajny w kierunku x(poziomym) z prędkością vx+ ruch jednostajnie opóźniony
po Hmax=> rzut poziomy
vx=v0*cos α vy=v0*sin α Z=vx*tc=
Zmax=sin2α=1 2α=90o=>α=45o Hmax=
b) spadek swobodny
H=
vk (prędkość końcowa)= gt
Hmax=
ważne! v0=vk ; tw=ts
14.Siła tarcia:
Jest to siła powodująca hamowanie. Wytracona w ten sposób energia zamienia się w ciepło i jest bezpowrotnie tracona. Siła tarcia jest skierowana w przeciwną stronę do kierunku ruchu. Jej wartość wyraża wzór:
Oznaczenia:
T - siła tarcia; f - współczynnik tarcia (cecha charakterystyczna danego materiału); N - siła nacisku (siła działająca pod kątem prostym do płaszczyzny styku trących powierzchni, najczęściej jest to składowa ciężaru)
Podstawowy podział tarcia:
tarcie zewnętrzne
tarcie ślizgowe
+ tarcie spoczynkowe (tarcie statyczne)
+ tarcie ruchowe (tarcie kinetyczne)
tarcie toczne
tarcie wewnętrzne
Współczynnik tarcia oznaczany μ [mi], k lub f jest wielkością charakteryzującą siłę tarcia. W zależności od rodzaju tarcia, wyróżnia się odpowiednie współczynniki tarcia.
Tarcie suwne
W tarciu suwnym czyli ślizgowym, współczynnik tarcia jest równy stosunkowi siły tarcia T do sił nacisku Fn ciała na podłoże (drugie ciało).
Współczynnik tarcia suwnego jest wielkością bezwymiarową.
Tarcie toczne
Dla tarcia tocznego współczynnik tarcia jest równy stosunkowi momentu tarcia tocznego Mt do siły nacisku N. Współczynnik ten ma wymiar wyrażany w jednostkach długości (np. mm).
15.WIELKOŚCI CHARAKTERYZUJĄCE RUCH HARMONICZNY
-wychylenie ciała z położenia równowagi x
x= Asinωt, gdzie ω-częstotliwość kołowa drgań (ω=
=2πf), f - częstotliwość, T-okres, a- amplituda wychylenia
-prędkość chwilowa
v=
Aωcosωt
vmax=Aω _maksymalna wartość prędkości
-przyspieszenie chwilowe
amax=Aω2-maksymalna wartość przyspieszenia
-energia 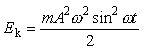
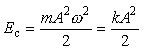
-siła zwracająca FZ- siła wywołująca ruch drgający
Fz=-kx, gdzie k=mω2-stała sprężystości
16. Ruch harmoniczny prosty - Każdy ruch powtarzający się w regularnych odstępach czasu nazywany jest ruchem okresowym. Jeżeli ruch ten opisywany jest sinusoidalną funkcją czasu to jest to ruch harmoniczny. Ciało porusza się ruchem harmonicznym prostym, jeżeli znajduje się pod wpływem siły o wartości proporcjonalnej do wychylenia z położenia równowagi i skierowanej w stronę położenia równowagi:
![]()
- siła, k - współczynnik proporcjonalności,
- wychylenie z położenia równowagi.
![]()
Równanie ruchu (skalarne dla kierunku OX) dla takiego ciała można zapisać (z II zasady dynamiki Newtona) jako:
albo w postaci różniczkowej:
Jest to równanie różniczkowe zwyczajne drugiego rzędu (występuje druga pochodna funkcji położenia x(t)).
Rozwiązania tego równania można równoważnie opisać za pomocą dowolnej z poniższych funkcji:
gdzie:
jest częstością kołową drgań,
stałe zależne od warunków początkowych.
Są to tzw. harmoniki. Rozwiązania są równoznaczne, a korzystając z tożsamości trygonometrycznych można znaleźć zależności pomiędzy powyższymi stałymi i rozwiązanie przedstawiać w dowolnej z postaci 1,2,3.
Częstość kołową ω0 wiąże z okresem drgań T związek:
, częstotliwość drgań ν natomiast wynosi
Ważną własnością ruchu harmonicznego jest to, że inne wielkości (prędkość, przyspieszenie) też są opisane przez równanie harmoniczne.
Energia w ruchu harmonicznym prostym
Energia potencjalna dla siły proporcjonalnej do wychylenia.
Wykres zależności energii od wychylenia
Z zasady zachowania energii, wynika zależność, z której można wyznaczyć energię kinetyczną:
Z równania powyższego wynika kilka faktów (na podstawie jedynki trygonometrycznej i porównania współczynników we wzorze
z powyższym):
![]()
Ciało drgające ma maksymalną prędkość gdy przechodzi przez położenie równowagi i ma ona wartość:
v0 = x0ω0, prędkość chwilowa zmienia się jak
Bezpośrednio z równania ruchu wynika, że przyspieszenie jest opisywane zależnością:
![]()
17. Ruch harmoniczny tłumiony - Ruch harmoniczny tłumiony występuje wtedy, gdy na ciało działa dodatkowo siła oporu ośrodka proporcjonalna do prędkości:
Równanie ruchu ma wtedy postać:
![]()
![]()
Rozwiązanie równania można wyrazić w postaci:
![]()
Przy czym przyjęto oznaczenie:
Wielkość ω jest nazywana zmodyfikowaną częstością drgań, jest zależna nie tylko od siły kierującej ale też od współczynnika tłumienia i maleje gdy współczynnik tłumienia rośnie.
![]()
Stałe A i B zależą od warunków początkowych następującymi związkami:
x0 - położenie początkowe, dla t = 0, v0 - prędkość początkowa, dla t = 0.
![]()
![]()
18. Ruch harmoniczny wymuszony - Oscylator może być pobudzany zewnętrznymi siłami. Stała siła nie zmienia drgań oscylatora harmonicznego, zmienia jedynie położenie równowagi oscylatora. Siła wymuszająca o charakterze oscylacyjnym zmienia częstość drgań oscylatora.
ω0 - częstość drgań własnych
Zmienną okresową siłę wymuszającą można przedstawić jako sumę funkcji harmonicznych cos(ωt).
![]()
Dlatego analizę równania można ograniczyć do:
ω - częstość siły wymuszającej,
A - amplituda przyspieszenia (siły na jednostkę bezwładności) wymuszającego,
β - współczynnik tłumienia
W przypadku gdy A = 0, uzyskuje się równanie oscylatora harmonicznego z tłumieniem, a gdy dodatkowo założymy że β = 0, równanie oscylatora prostego.
19. Wahadło matematyczne - (proste) każdy punkt materialny zawieszony na cienkiej, nieważkiej, nierozciągliwej nici. Wahadło wychylone z położenia równowagi, zaczyna ruch drgający pod wpływem siły ciężkości F=mg. Siłę ciężkości można podzielić na dwie składowe : FN działa w kierunku nici, a FS w kierunku do niej prostopadłym.
![]()
I składowa równoważy siłę naprężenia:
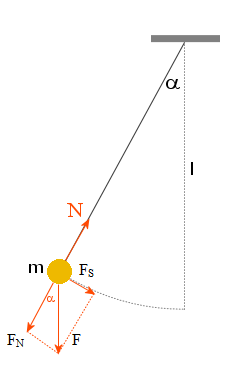
II Składowa dostarcza niezbędnego przyspieszenia dośrodkowego do utrzymania ruchu po łuku okręgu; siła ta jest zwrócona przeciwnie do przesunięcia, więc:
m-masa ciała
g -przyspieszenie ziemskie 9,81[m/s2]
α - kąt wychylenia
Przemieszczenie wzdłuż łuku wynosi:
![]()
i dla małych kątów ruch jest w przybliżeniu prostoliniowy.
Przyjmując, że:
sinα ≈ α
![]()
![]()
![]()
![]()
Wzór na okres drgań(czas jednego pełnego wahnięcia):
![]()
l-długość wahadła
g- przyspieszenie ziemskie 9,81[m/s2]
Okres nie zależy od masy wahadła.
Izochronizm - okres wahadła matematycznego nie zależy od wychylenia.
20. Energia w ruchu drgającym harmonicznym prostym.
A. Energia potencjalna
Ciało drgające ruchem harmonicznym prostym posiada energię potencjalną wtedy, gdy znajduje się ono w jakimś wychyleniu od stanu równowagi. Gdy ciało znajduje się więc w położeniu równowagi, nie posiada energii potencjalnej.
Energia potencjalna jest równa energii potencjalnej sprężystości, którą możemy wyrazić wzorem:
![]()
Maksymalna wartość energii potencjalnej wynosi:
i ciało ma tę energię wtedy, gdy znajduje się w położeniu maksymalnego wychylenia (amplitudy).
![]()
B. Energia kinetyczna
Ciało o masie m drgające ruchem harmonicznym prostym posiada energię kinetyczną wtedy, gdy posiada ono jakąś prędkość v w danej chwili. Oznacza to, że ciało nie posiada energii kinetycznej wtedy, gdy prędkość równa jest zeru, a taki moment następuje, gdy ciało znajduje się w położeniu maksymalnego wychylenia (x = A). Energię kinetyczną wyrażamy wzorem:
![]()
Maksymalna wartość energii kinetycznej wynosi
i mamy z nią do czynienia, gdy drgające ciało ma największą prędkość (a jak wiemy, ma ono ją wtedy, gdy znajduje się w punkcie równowagi x = 0).
C. Energia mechaniczna (całkowita)
![]()
E = K + U = EK + EP
Całkowita energia punktu materialnego poruszającego się ruchem harmonicznym prostym jest proporcjonalna do kwadratu amplitudy tego ruchu.
21. Składanie ruchów harmonicznych prostych.
Krzywe Lissajous - jest to nałożenie się dwóch harmonicznych drgań wzajemnie prostopadłych.
22. Ruch falowy(wielkości charakterystyczne, podział ruchów):
Fala - zaburzenia ośrodka rozchodzące się w czasie i przestrzeni; ruch fal jest ruchem jednostajnym ![]()
; wyróżniamy:
Fale mechaniczne
-poprzeczne - punkty materialne ośrodka drgają w kierunku prostopadłym do kierunku rozchodzenia się fali
-podłużne - punkty materialne ośrodka drgają w tym samym kierunku co fala
Fale jednowymiarowe
Fale dwuwymiarowe
Trójwymiarowe
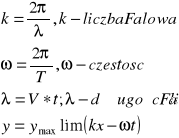
Fala posiada:
- Czoło fali - miejsce geometryczne punktów drgających o jednakowej fazie. Ze względu na kierunek czoła fali wyróżniamy: fale płaskie i fale kuliste
- Długość fali - długość na jaka rozchodzi się fala w ciągu okresu
![]()
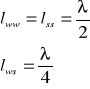
Fala składa się z:
-Węzłów (pkty o zerowej amplitudzie)
- Strzałek (pkty o maksymalnej amplitudzie)![]()
- odległość miedzy węzłem a strzałką
Zjawiska falowe:
-Interferencja - nakładanie się spójnych fal z różnych źródeł, które prowadzi do wzmocnienia lub wygaszenia fali
-Dudnienie - okresowe zmiany amplitudy drgań powstałe ze złożenia dwóch drgań o zbliżonych częstotliwościach
-Superpozycja - nakładanie się fal niespójnych np. szum
23. Fala stojaca - jest przykładem interferencji fal. Powstaje w wyniku nałożenia się dwóch biegnących w przeciwnych kierunkach fal w ośrodku uformowanym i ograniczonym(np. pręt stalowy). Częstotliwości fal stojących nie są dowolne, lecz precyzyjnie określone przez właściwości ośrodka, noszą nazwę Drgań własnych - wyraza to wzór ![]()
, dla n=1 - drgania podstawowe dla n>1 - drgania wyższego rzędu-drgania harmoniczne (v - prędkośc fali w pręcie, l - długośc pręta)
24. Fale dźwiękowe - to fale podłużne i mechaniczne. Rozchodzą się w cieczach, gazach i ciałach stałych (w próżni nie).
0 - 16 Hz - poddźwięk (infradźwięki)
16 - 16 * 104 Hz -dźwięki (fale dźwiękowe)
16 * 104 - 16 * 109 Hz - ultradźwięki
>GHz - hiperdźwięki ( do 1012 Hz)
Cechy dźwięku:
wysokości ( wzrost częstotliwości + wzrost dźwięku)
barwa ( złożenie tonu podstawowego i tonów harmonicznych)
natężenie dźwięku:
![]()
![]()
![]()
I - natężenie s - powierzchnia prostopadła
W - energia p - moc
t - czas
granica słyszalności (próg) - najniższa wartość 10-12 [W/m2]
próg wrażenia bólu - maksymalne natężenie dźwięku
![]()
Prawo Webera - Fechnera - Wrażenia słuchowe odbierane przez ucho nie są proporcjonalne do natężenia dźwięku, lecz logarytmu natężenia dźwięku.
Współczynnik pochłaniania - zależy od materiału z którego wykonane jest pomieszczenie
25. Ultradźwięki - fale mechaniczne rozchodzące się w ośrodku sprężystym z częstotliwością 20 ktk - 16 GHz. Wykorzystanie:
- położnictwo
- onkologia
- kardiologia
- okulistyka
- neurochirurgia
- chirurgia naczyniowa
Ultrasonografia (USG) - to badanie narządów wewnętrznych za pomocą fal ultradźwiękowych. Metoda diagnostyczna jest oparta na zjawisku echa ultradźwiękowego. Informacje uzyskane tą metodą mogą być przedstawione na ekranie oscyloskopowym w postaci impulsów, lub w postaci obrazu rozkładu tkanek normalnych i patologicznych. Wykorzystanie:
- mikromasaże
- nóż chirurgiczny
- rozbijanie bakterii, wirusa grypy
- badanie mózgu
- obraz płodu
26.Zjawisko Dopplera - polega na zmianie częstotliwości w przypadku względnej zmiany odległości miedzy źródłem dzwięku a obserwatorem.
Obserwator przybliża się do źródła - 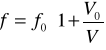
![]()
- prędkość obserwatora, ![]()
- prędkość dźwięku w powietrzu.
Obserwator oddala się od źródła - 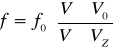
![]()
- prędkość źródła ( znak w liczniku `+' i w mianowniku `-` odpowiadają sytuacji, gdy obserwator i źródło poruszają się w jednym kierunku, a znak `-` w liczniku i w mianowniku `+' mówią, ze obserwator i źródło oddalają się od siebie).
27. Gaz Modelowy do opisu-gaz doskonaly:
Równanie Clapeyrona-z pkt makroskopowego
pV=RTn
R-stała(8,31 J/mol*K)
T-tepm w Kelvinach
n-liczba moli [ (n=m/μ ) m-masa, μ-masa cząsteczkowa]
Gaz doskonaly definiujemy z pkt mikroskopowego:
Gaz składa się z cząsteczek, które można traktować jak punkty materialne. Gdy gaz jest pierwiastkiem lub związkiem chemicznym(stały) wszystkie cząsteczki gazu uważamy za identyczne
Cząsteczki gazy poruszają się chaotycznie i podlegają zasadom dynamiki Newtona
Całkowita liczba cząsteczek gazu jest bardzo duża
NA=6,023*1023 cząsteczki/mol -liczba Avogadro
Stała Boltzmana
k=R/NA k=1,38*1023 J/K
Objętość cząsteczek gazu stanowi niewielką część objętości zajmowanej przez gaz(objętość cząsteczki można ominąć)
Poza momentem zderzenia na cząsteczki nie działają żadne siły. Zasięg oddziaływania sił międzycząsteczkowych jest porównywalny z rozmiarem czaseczek
Zderzenia cząsteczek są sprężyste a czas ich trwania jest do pominięcia
p=F/s[n/m2=Pa] p-ciśnienie
28.Kinetyczna interpretacja temperatury
Średnia energia kinetyczna cząstki w temperaturze T wynosi:
Równanie powyższe dostarcza również interpretacji temperatury:
Skale temperatur można podzielić na dwie klasy:
Teoretyczne - oparte na zależnościach teoretycznych (idealnych). Przykładem
może być termodynamiczna skala temperatur lub skala gazu doskonałego.
Empiryczne - oparte na danych doświadczalnych np.
Przykłady skal tempartur:
Termodynamiczna skala temperatury wg koncepcji Kelvin'a. teoretyczna skala oparta na sprawności cyklu Carnota. Jednostką tej skali jest Kelvin (K) - jednostka podstawowa Międzynarodowego Układu Jednostek Miar SI.
Skala temperatury Celsjusza:, oparta na dwóch punktach stałych: t1=0oC (temperatura topnienia lodu), t2=100oC (temperatura wrzenia wody).
Oba te punkty określone są pod ciśnieniem 101325 N/m2 [Pa] = 1 atmosfera.
Jednostką jest stopień Celsjusza (ozn. oC).
Skala temperatury Fahrenheita: empiryczna skala temperatury oparta na dwóch punktach stałych: t1=0oF (temperatura mieszania śniegu z salmiakiem) i t2=100oF (temperatura normalna ciała ludzkiego). Skala ta jest stosowana głównie w krajach posługujących się
angielskim i amerykańskim systemem miar.
29. Równanie Clapeyrona, równanie stanu gazu doskonałego to równanie stanu opisujące związek pomiędzy temperaturą, ciśnieniem i objętością gazu doskonałego, a w sposób przybliżony opisujący gazy rzeczywiste. Sformułowane zostało w 1834 roku przez Benoîta Clapeyrona. Prawo to można wyrazić wzorem
pV=nRT
gdzie: p-ciśnienie, v-objętość, n-liczba moli gazu, T-temperatura, R-uniwersalna stała gazowa.
Równanie to jest wyprowadzane na podstawie założeń:gaz składa się z poruszających się cząsteczek, cząsteczki zderzają się ze sobą oraz ze ściankami naczynia w którym się znajdują, brak oddziaływań międzycząsteczkowych w gazie, z wyjątkiem odpychania w momencie zderzeń cząsteczek, objętość (rozmiary) cząsteczek jest pomijana, zderzenia cząsteczek są doskonale sprężyste.
30. Równanie Van der Waalsa (1836-1923) - równanie stanu gazu wiążące parametry stanu gazu (ciśnienie p, objętość V i temperaturę T). Wyprowadzone 1873 r. jako rozszerzenie równania stanu gazu idealnego (równanie Clapeyrona), wprowadził poprawkę uwzględniającą objętość cząsteczek gazu oraz oddziaływanie wzajemne cząsteczek gazu. pV=nRT
a, b - stała charakterystyczna dla danego gazu, p - ciśnienie, V - objętość, n - liczność (ilość gazu) w molach, T - temperatura bezwzględna, R - uniwersalna stała gazowa,
- ciśnienie wewnętrzne
31. Przemiany Gazowe:
-przemiana izotermiczna - zachodzi, gdy temperatura jest stała, ciśnienie i objętość zmieniają się odwrotnie do siebie.
-przemiana izobaryczna - zachodzi, gdy ciśnienie gazu nie ulega zmianie (jest stałe). Objętość i temperatura gazu w tej przemianie zmieniają się wprost proporcjonalnie do siebie.
-przemiana izochoryczna - zachodzi, gdy objętość gazu nie ulega zmianie (stała objętość naczynia) a ciśnienie i temperatura gazu zmieniają się wprost proporcjonalnie do siebie.
-przemiana adiabatyczna - jest to przemiana w której nie ma wymiany ciepła z otoczeniem i wszytskie parametry określające stan gazu (p, V, T) ulegaj zmianie.
32. I zasada termodynamiki - jest sformułowaniem zasady zachowania energii dla układów termodynamicznych. Zasada stanowi podsumowanie równoważności ciepła i pracy oraz stałości energii układu izolowanego. Dla układu zamkniętego (nie wymienia masy z otoczeniem, może wymieniać energię) zasadę można sformułować w postaci:
Zmiana energii wewnętrznej układu zamkniętego jest równa energii, która przepływa przez jego granice na sposób ciepła lub pracy.
![]()
ΔU - zmiana energii wewnętrznej układu,Q - energia przekazana do układu jako ciepło,
W - praca wykonana na układzie.
Wprowadzając pojęcie perpetuum mobile, czyli maszyny wykonującej dowolnie długo pracę bez pobierania energii z zewnątrz, można sformułować pierwszą zasadę termodynamiki w następujący sposób: „Nie istnieje perpetuum mobile pierwszego rodzaju”.
33. II zasada termodynamiki - stwierdza, że w układzie termodynamicznie izolowanym istnieje funkcja stanu zwana entropią S, której zmiana ΔS w procesie adiabatycznym spełnia nierówność
, przy czym równość zachodzi wtedy i tylko wtedy, gdy proces jest odwracalny. W uproszczeniu można to wyrazić też tak: "W układzie termodynamicznie izolowanym w dowolnym procesie entropia nigdy nie maleje". Najszerzej znane alternatywne sformułowania pochodzą od Clausiusa: "Ciepło nie może samorzutnie przepływać od ciała o temperaturze niższej do ciała o temperaturze wyższej" oraz od Lorda Kelvina: „Nie jest możliwy proces, którego jedynym skutkiem byłoby pobranie pewnej ilości ciepła ze zbiornika i zamiana go w równoważną ilość pracy".
34. III zasada termodynamiki - nie można za pomocą skończonej liczby kroków uzyskać temperatury zera bezwzględnego (zero kelwinów), jeżeli za punkt wyjścia obierzemy niezerową temperaturę bezwzględną. Inne sformułowanie głosi, że entropia substancji tworzących doskonałe kryształy dąży do 0 gdy temperatura dąży do 0 K. Mówiąc jaśniej, gdyby udało się schłodzić jakąś substancję do 0 K i gdyby ona utworzyła kryształ doskonały to jej entropia musiałaby przyjąć wartość 0. Jest to jednak technicznie, a także formalnie niewykonalne, dlatego definicja trzeciej zasady termodynamiki w formie: „entropia kryształu doskonałego w temperaturze zera bezwzględnego jest równa 0” nie jest poprawna, choć intuicyjnie akceptowalna.
35. Energia wewnętrzna (oznaczana zwykle jako U lub Ew) w termodynamice - całkowita energia układu będącą sumą energii oddziaływań międzycząsteczkowych i wewnątrzcząsteczkowych układu, a także energii ruchu cieplnego cząsteczek oraz wszystkich innych rodzajów energii występujących w układzie. Energia wewnętrzna jest jednym z potencjałów termodynamicznych. W przypadku gazu doskonałego: ၄U = ၄Ek = nCv၄T, n - liczba moli gazu, CV - ciepło molowe przy stałej objętości,T - zmiana temperatury gazu.
Entropia - miara (prawdopodobieństwo) uporządkowania układu cząstek. Im jest wyższa, tym większy jest nieporządek. s = klnp, k - stała Boltzmana, p - prawdopodobieństwo stanu nieporzadku
Energia swobodna - w termodynamice, część energii układu fizycznego, która może być przekształcona w pracę. Wyróżniamy:
energię swobodną Helmholtza - część energii całkowitej układu, która może być zamieniona na pracę w procesie o stałej temperaturze,
entalpię swobodną - część energii całkowitej układu, która może być zamieniona na pracę w procesie o stałej temperaturze i ciśnieniu.
Entalpia (H) (zawartość ciepła) — w termodynamice wielkość fizyczna będąca funkcją stanu mająca wymiar energii, będąca też potencjałem termodynamicznym, oznaczana przez H, h,I lub χ, którą definiuje zależność: H = U + pV, H - entalpia układu, U — energia wewnętrzna układu, p — ciśnienie, V— objętość
Entalpia swobodna - potencjał termodynamiczny zwany funkcją Gibbsa lub energią swobodną Gibbsa, oznaczany przez G. G = U + p၄V - TS, U - energia wewnętrzna układu, S - entropia układu, p,V - ciśnienie i objętość układu, T - temperatura bezwzględna układu
W entalpii swobodnej potencjał termodynamiczny Gibbsa jest maksymalną pracą nie związaną ze wzrostem objętości (pracy nieobjętościowej, możliwej do uzyskania z zamkniętego układu i może osiągnąć swoje maksimum w procesie odwracalnym izotermiczno-izobarycznym).
b
a
c
a
c
b
a
ay
x
ax
y
a2
a1
a
k
j
i
x
y
z
![]()
![]()
![]()
![]()
![]()
![]()
30-50 dB - rozmowa, 80 dB - ruch uliczny
120 - 130 dB - samolot, 100-110 dB - pistolet
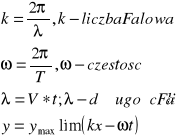
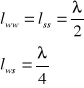
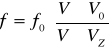
![]()
Wyszukiwarka
Podobne podstrony:
PROFILAKTYKA egzamin WSZYSTKO, Dokumenty UŚ Pedagogika resocjalizacyjna, 4 sem, Profilaktyka społecz
psychopatol- całość, pedagogika - dokumenty
Polecam wszystkim, Dokumenty(3)
MATERIAŁY OD P ZAREMBY WSZYSTKO W 1 DOKUMENCIE, EDUKACJA POLONISTYCZNA, PSYCHOLOGIA, SOCJOLOGIA, ED
Skróty klawiaturowe Worda - wszystkie, Dokumenty Textowe, Komputer
badanie fizykalne wszystko całość wazne
fizyka egzamin odpowiedzi, studia calosc, studia całość, fizyka
fiza cw 22 wszystko, Fizyka
Fizyka calosc kolos1
103, Studia Politechnika Poznańska, Semestr II, I pracownia fizyczna, LABORKI WSZYSTKIE, FIZYKA 2, F
204pl, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria z 1 prac
spr5, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA] Laborki, laboratorium stare, bartochowsk
Fizyka - dokumenty, CWICZ D1, M3
C4 - Roztrzepaniec, Pomoce naukowe SGSP, Moje Dokumenty, fizyka zad
FIZYKA I wszystko
fizyka+calosc+git 1 KBYRIASGCQLFFFCOFTN7FUTYJDMTUDHIX522TTQ
więcej podobnych podstron