1.5 Si

ły bezwładności.

Za

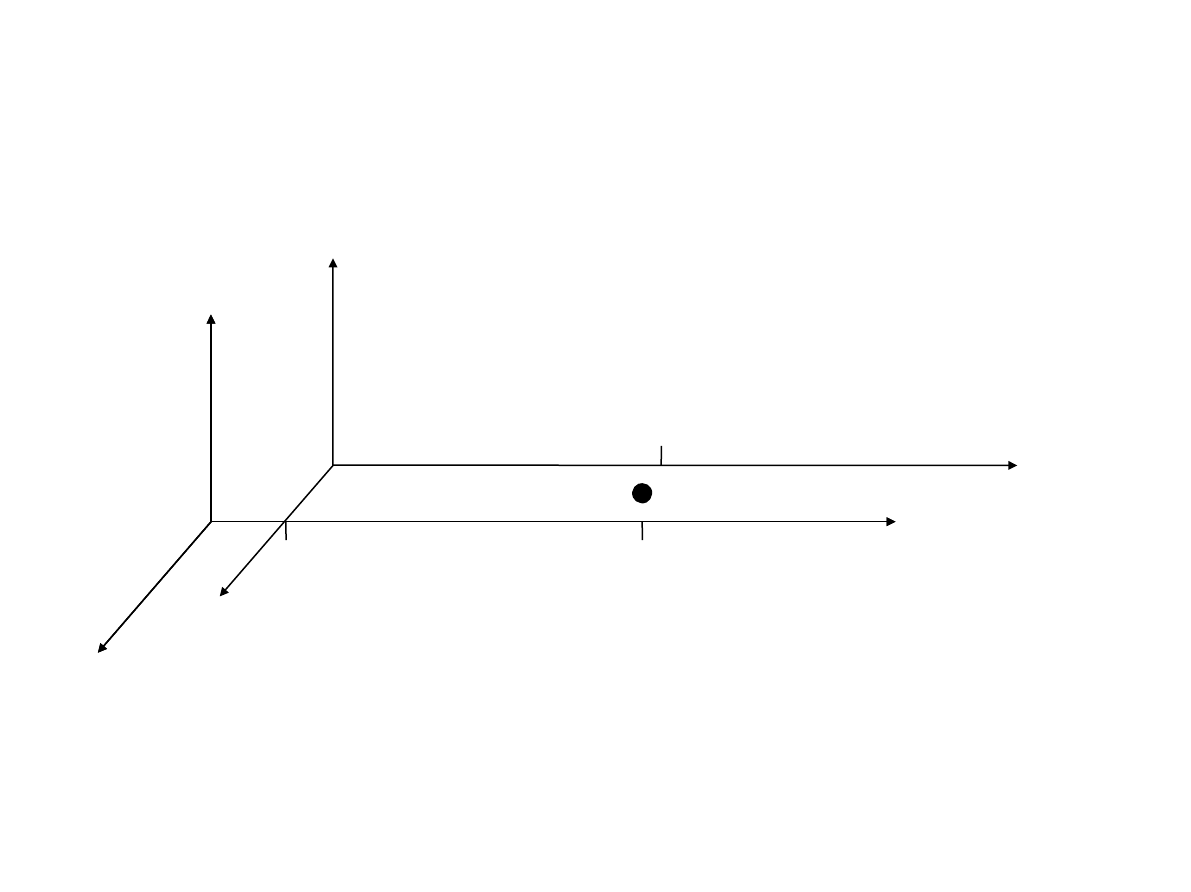
łóżmy, że obserwujemy ruch punktu materialnego A w pewnym

inercjalnym uk

ładzie odniesienia (na rysunku oznaczonym przez O).

z`

z

A

x(t)

x`(t)

x`

x

y`

y

Niech rozwa

żany punkt znajduje się pod działaniem innych ciał

materialnych, wi

ęc porusza się ruchem przyspieszonym.

O`

O

x

o

(t)

Zgodnie z drug

ą zasadą dynamiki:



F



d p



d

(m



v )



m



a .







dt

dt

(1.5.1)

Dla uproszczenia za

łóżmy, że punkt porusza się wzdłuż osi x, wtedy

warto

ść przyspieszenia można wyrazić wzorem:



d x(t)

.



| a |



a

dt

2

2

x

(1.5.2)

W

eźmy teraz pod uwagę drugi układ odniesienia O`, poruszający

si

ę względem układu O w kierunku osi x ruchem dowolnym.

W uk

ładzie O współrzędna punktu A wynosi x(t), w układzie O`

natomiast x`(t). Oznaczaj

ąc przez x

o

(t) odleg

łość początku układu

O` od pocz

ątku układu O można napisać związek:

x`(t)



x(t)



x

o

(t)

(1.5.3)

Po dwukrotnym zr

óżniczkowaniu równania (1.5.3 ) względem czasu

otrzymujemy:

x

o

(t)

,

d x`(t)



d x(t)



d

dt

2

2

dt

2

2

2

dt

2

(1.5.4)

czyli

a`



a



a

o

,

(1.5.5)

gdzie a` i a oznaczaj

ą odpowiednio przyspieszenia punktu A

wzgl

ędem układów O` i O, a

o

to przyspieszenie uk

ładu O` względem

uk

ładu O. Ze związku (1.5.5) widać, że przyspieszenie w układzie O`

nie jest w og

ólności równe przyspieszeniu w układzie O. Równość

zachodzi tylko wtedy, gdy a

o

= 0, a wi

ęc gdy przyspieszenie układu

O` wzgl

ędem układu O jest równe zero (tzn. gdy układ O` jest

uk

ładem inercjalnym). Jeżeli a

o

nie jest

równe zero, to układ O`

nazywamy nieinercjalnym. W przypadku ruchu w przestrzeni
t

rójwymiarowej wzór (1.5.5)należy zapisać w postaci wektorowej:







a`



a



a

o

(1.5.6)

Mno

żąc obie strony równania (1.5.6) przez masę m otrzymujemy:











m



a`



m



a



m



a

o



F



m



a

o

.

Animacja: WeightOfAPersonRidingInAnElevator

(1.5.7)

W uk

ładzie nieinercjalnym O` nie obowiązuje zatem pierwsza

zasada
dynamiki. Punkt materialny, na kt

óry nie działa żadna siła, nie

spoczywa, lecz porusza si

ę z przyspieszeniem:





a`

 

a

o

(1.5.8)

Nie obowi

ązuje w nim również druga zasada dynamiki. Iloczyn

masy i przyspieszenia nie jest r

ówny sile działającej na dana masę,

lecz sile minus wyr

ażenie m



a

o

.

Zdefiniujmy teraz

si

łę bezwładności

w nast

ępujący sposób:







F

b

 

m



a

o

(1.5.9)

Wz

ór (1.5.7) przyjmuje teraz postać:







m



a`



F



F

b

.

(1.5.10)

Ze wzoru (1.5.10) wynika,

że drugą zasadę można stosować w

uk

ładach nieinercjalnych, jeżeli do sił działających na punkt

materialny ze strony innych cia

ł, dodamy siłę bezwładności.

Ponadto w uk

ładzie nieinercjalnym, względem którego





przyspieszenie cia

ła jest równe zeru (

a`



0

) suma s

ił

F



dzia

łających na to ciało oraz siły bezwładności

jest

równa zeru:

F

b

Wz

ór (1.5.11) jest matematycznym zapisem tzw.

zasady d

’ Alemberta

.

Z

siłami bezwładności spotykamy się przy obserwacji zjawisk

zwi

ązanych z ruchem przyspieszonym. Na przykład w obracającym

si

ę układzie odniesienia występuje siła bezwładności, nazywana

od

środkową siłą bezwładności:





F



F

b



0

(1.5.11)

Innym przyk

ładem siły bezwładności jest

s

iła Coriolisa

dzia

łająca

na cia

ło poruszające się ruchem postępowym w obracającym się

uk

ładzie odniesienia:



 

F

C



2



m



v



ω

(1.5.13)



ω



v

m

- pr

ędkość kątowa z jaką obraca się układ odniesienia

- pr

ędkość liniowa poruszającego się ciała

- masa poruszaj

ącego się ciała

Si

ła Coriolisa powoduje na przykład silniejsze podmywanie

prawego brzegu rzek na p

ółkuli północnej.



ω



r



v





F

od



m





2

r .



F

od

m

(1.5.12)

Film

„loop”.

Film

„rollercoaster”.

1.6 Praca, moc.

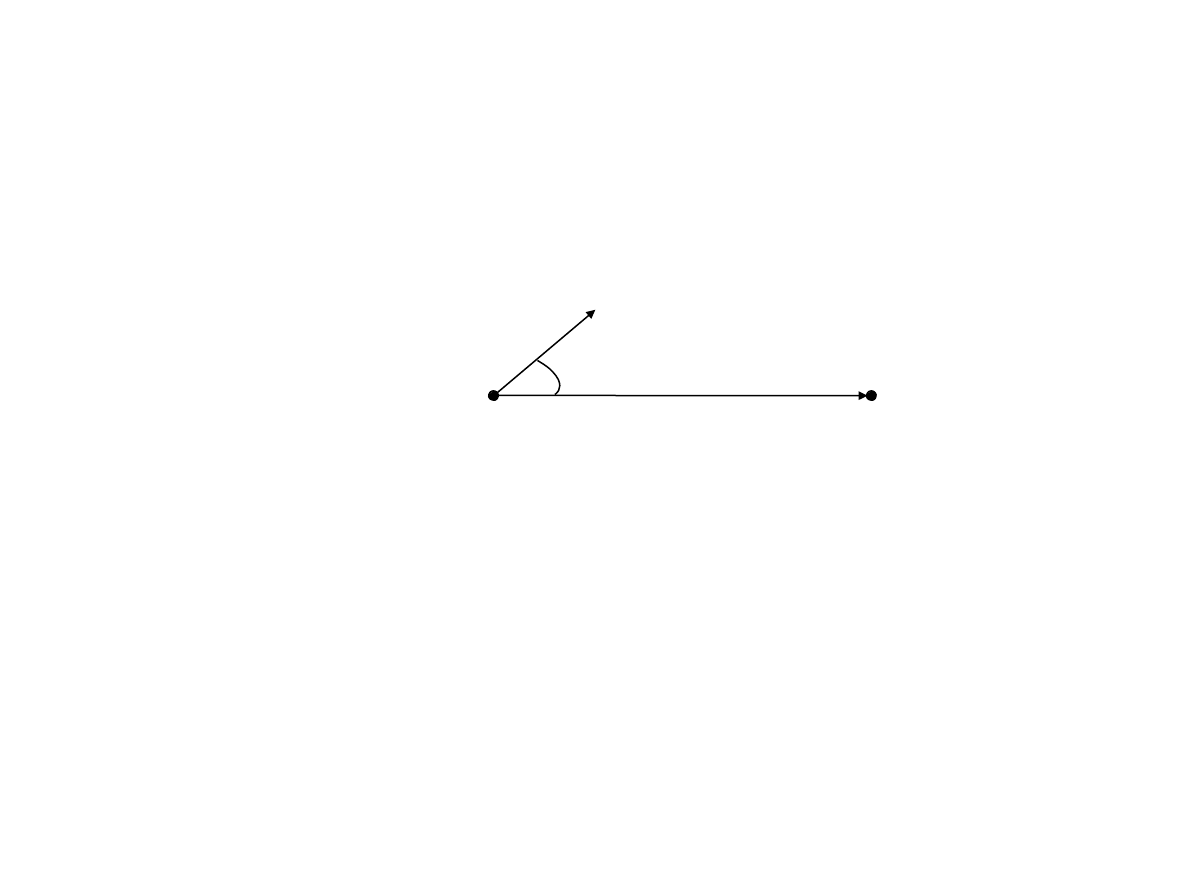
Rozwa

żmy przesunięcie ciała



dzia

łania siły

F

:



F



s

wz

dłuż linii prostej pod wpływem

A

B



Zak

ładamy, że podczas całej drogi AB wartość wektora

F

i

kąt α są stałe. W takim przypadku pracę W siły

F

na drodze

s

okre

ślamy wzorem:





s





 





W



F



s



| F || s | cos



.

(1.6.1)

Animacja: MechanicalWork

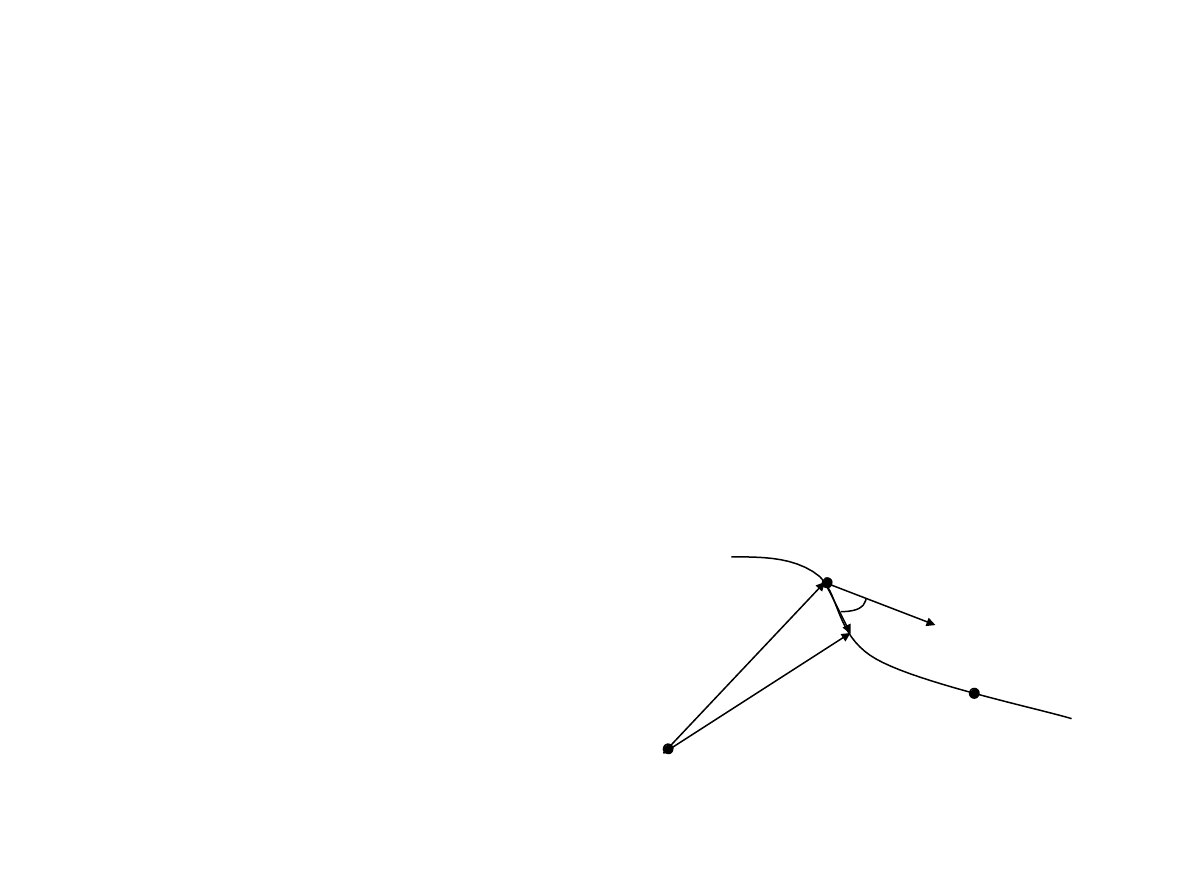
W przypadku og

ólnym (kiedy ciało porusza się po torze krzywoliniowym)

Elementarna praca dW, jak

ą należy wykonać w trakcie przesunięcia





odpowiadaj

ącego zmianie wektora położenia ciała

r

o

d r

,

jest okr

eślone wzorem:





dW



F



d r .

Ca

łkowitą pracę wykonaną w trakcie przesunięcia z punktu A

do punktu B wyznaczajmy ca

łkując elementarne prace z

(1.6.2)

po ca

łej drodze przesunięcia, czyli obliczamy całkę krzywoliniową

(1.6.2)

B





W





F



d r .

A

(1.6.3)



r





r



dr



d r

A

B

O



F



W przypadku, gdy na przyspieszane cia

ło nie działają żadne siły oporu

o

środka, w którym się ono porusza, wykonana praca W jest równa

energii kinetycznej E

k

, jak

ą ciało nabyło w wyniku przyspieszenia:

.

2

mv

2

W



E

k



(1.6.4)

Moc

średnią

pracy

ΔW wykonanej w czasie

Δt obliczy ze wzoru:

 

W

.



t

P

śr

(1.6.5)

Moc chwilow

ą

pracy definiujemy nast

ępująco

:

P



lim



W



dW

.



t



0



t

dt

(1.6.6)

Podstawiaj

ąc wyrażenie

(1.6.2) do (1.6.6) otrzymujemy zale

żność:

 



F



v ,



d r



P



F



dt



v

- chwilowa pr

ędkość ciała.

(1.6.7)

Film

„Praca, moc, energia” (od 1min , od 6 min 5s do 24 min)

1.7 Opory ruchu.

W skali pojedynczych ato

mów powierzchnie stykających się ciał są

nieregularne. Mechanizm strat energii polega na tym,

że gdy ślizgające

si

ę ciało trafia na nierówności, powstają odkształcenia ciał oraz ruchy

at

omów, co po pewnym czasie powoduje ogrzanie obu ciał.

Wielko

ść siły

tarcia po

ślizgowego

(wyst

ępującego w ruchu posuwistym)

okre

śla wzór:

F

N

- warto

ść siły nacisku ciała (składowej prostopadłej

do powierzchni po

ślizgu)

(1.7.1)

Animacja: StaticFriction

F

T

 

F

N



,





v

v



-wsp

ółczynnik tarcia poślizgowego



v



v

- wersor skierowany w kierunku ruchu cia

ła

Si

ła tarcia poślizgowego

F

T

nie zale

ży od pola geometrycznej

powierzchni styku cia

ł. Zależy ona od pola rzeczywistej powierzchni

styku na kt

órą ma wpływ stan powierzchni stykających się ciał

(wsp

ółczynnik μ we wzorze

(1.7.1))

i s

iła dociskająca

F

N

.

Ws

półczynnik tarcia poślizgowego ma z reguły różne wartości w chwili

rozpocz

ęcia ruchu (

ws

półczynnik tarcia statycznego



S

) oraz w trakcie

ruchu (

wsp

ółczynnik tarcia kinetycznego



k

), przy czym



S

>



k

.

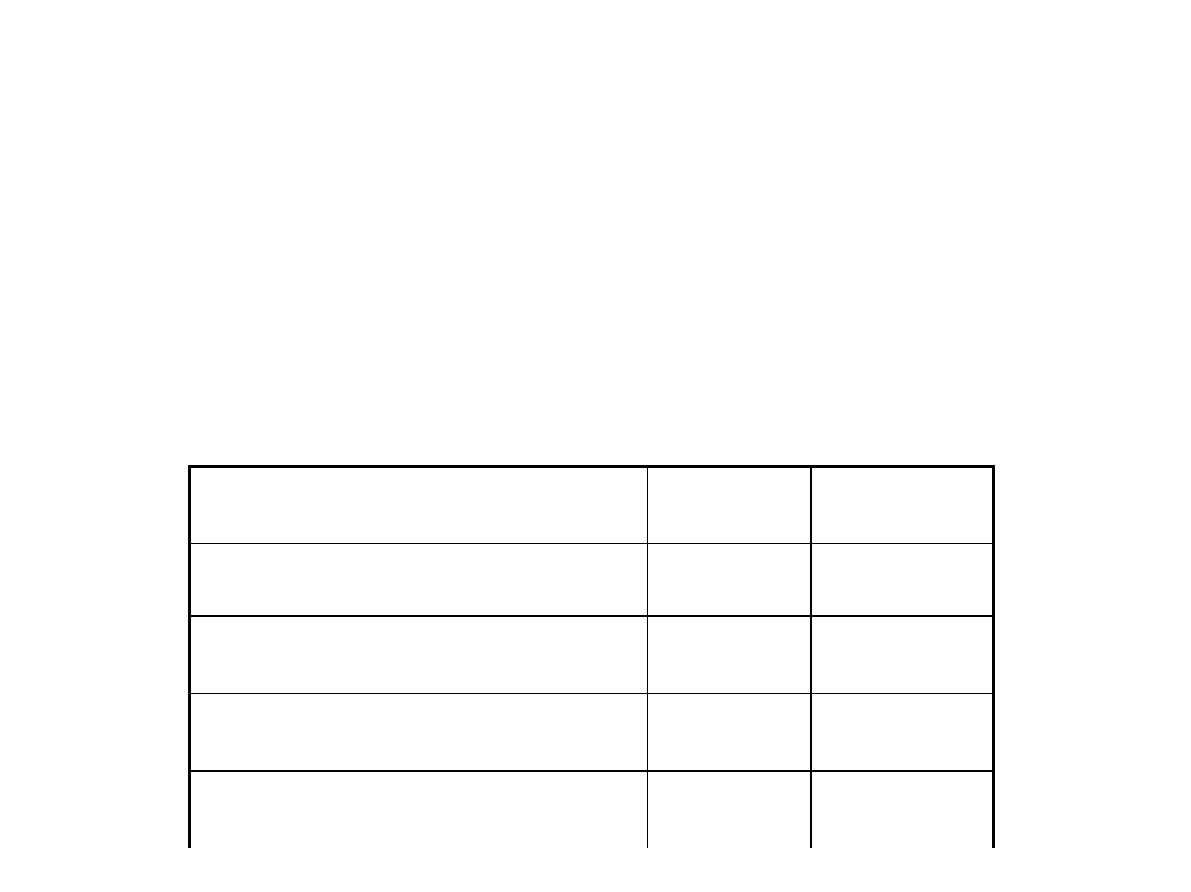
Przyk

ładowe wartości:



Materiał



S



k

opona – suchy beton

1.0

0.7

opona – mokry beton

0.7

0.5

teflon - teflon

0.04

0.04

stal - stal

0.15

0.03 – 0.09

Wprowadzeniu smaru pomi

ędzy trące o siebie powierzchnie zmienia

charakter oddzia

ływań molekularnych. Zamiast oddziaływań

pomi

ędzy atomami trących o siebie ciał mamy oddziaływania:

atom pod

łoża - atom smaru

atom smaru - atom smaru
atom smaru - atom t

rącego ciała.

O sile tarcia decyduj

ą wówczas siły najsłabszych oddziaływań. Z

reg

uły są to oddziaływania pomiędzy cząsteczkami smaru.

Innym rodzajem si

ł tarcia są siły

oporu toczenia

.

Warunkiem wprawienia cia

ła w ruch toczny (czyli pokonanie sił tarcia

tocznego) jest zadzia

łanie momentu sił (rysunek poniżej):







M



r



F ,

(1.7.2)

F

- si

ła wprawiająca ciało w ruch



- wektor po

łożenia punktu przyłożenia siły względem

chwilowej osi obrotu O.



r



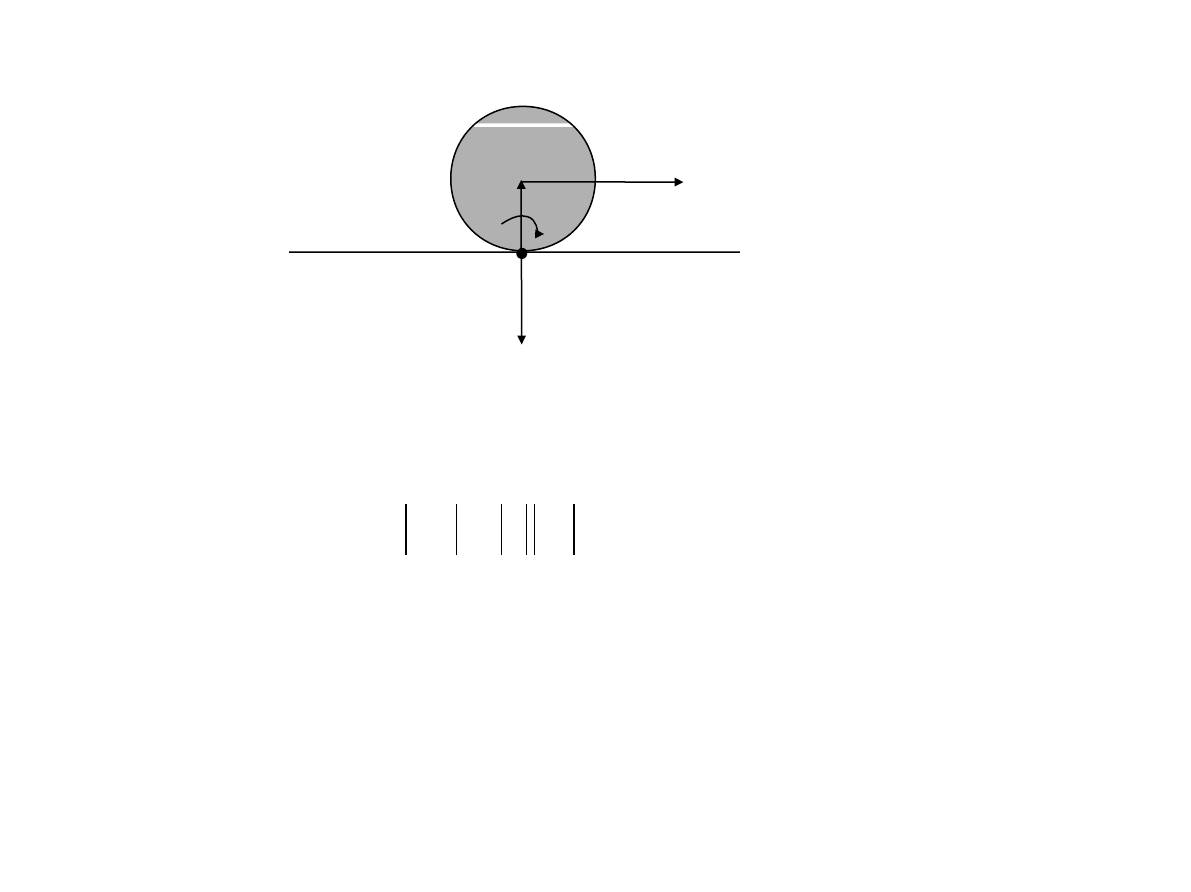
F



r

O



F

N



W przypadku, gdy si

ła

otrzymujemy:



F

dzia

ła w kierunku równoległym do podłoża



 

M



M



r F



rF .

(1.7.3)

Z do

świadczenia wynika, że wartość M momentu siły potrzebnego do

pokonania opo

rów toczenia jest proporcjonalna do siły nacisku

F

N

danego cia

ła na podłoże:

M





T

F

N

,

(1.7.4)

przy czym wsp

ółczynnik proporcjonalności



T

nazywany jest

wsp

ółczynnikiem tarcia toczenia

.

Wsp

ółczynnik tarcia toczenia ma wymiar długości ( [m] ).

Podstawiaj

ąc wzór

(1.7.3) do (1.7.4) mamy

F

N

.

r

F





T

(1.7.5)

Z pow

yższego wzoru wynika, że aby toczyć dane ciało należy użyć

si

ły proporcjonalnej do siły nacisku

F

N

i odwrotnie

proporcjonalnej do promienia krzywizny r.

Film

„Przyczyny tarcia” .

Film

„Opory ruchu” ( do 7 min 30 s).

2. Elektryczno

ść i magnetyzm.

2.1 Elektrostatyka.

2.1.1 Prawo Coulomba. Pole elektrostatyczne.

Elektrostatyka

zajmuje si

ę badaniem pól elektrycznych wytworzonych

przez nieruchome

ładunki.

W przyrodzie wyst

ępują ładunki dodatnie i ujemne, które ze sobą

oddzia

łują, przy czym ładunki różnoimienne się przyciągają, a

jednoimienne si

ę odpychają.

Dla

ładunków punktowych siła jest wprost proporcjonalna do iloczynu

ich

ładunków i odwrotnie proporcjonalna do kwadratu odległości

mi

ędzy nimi:

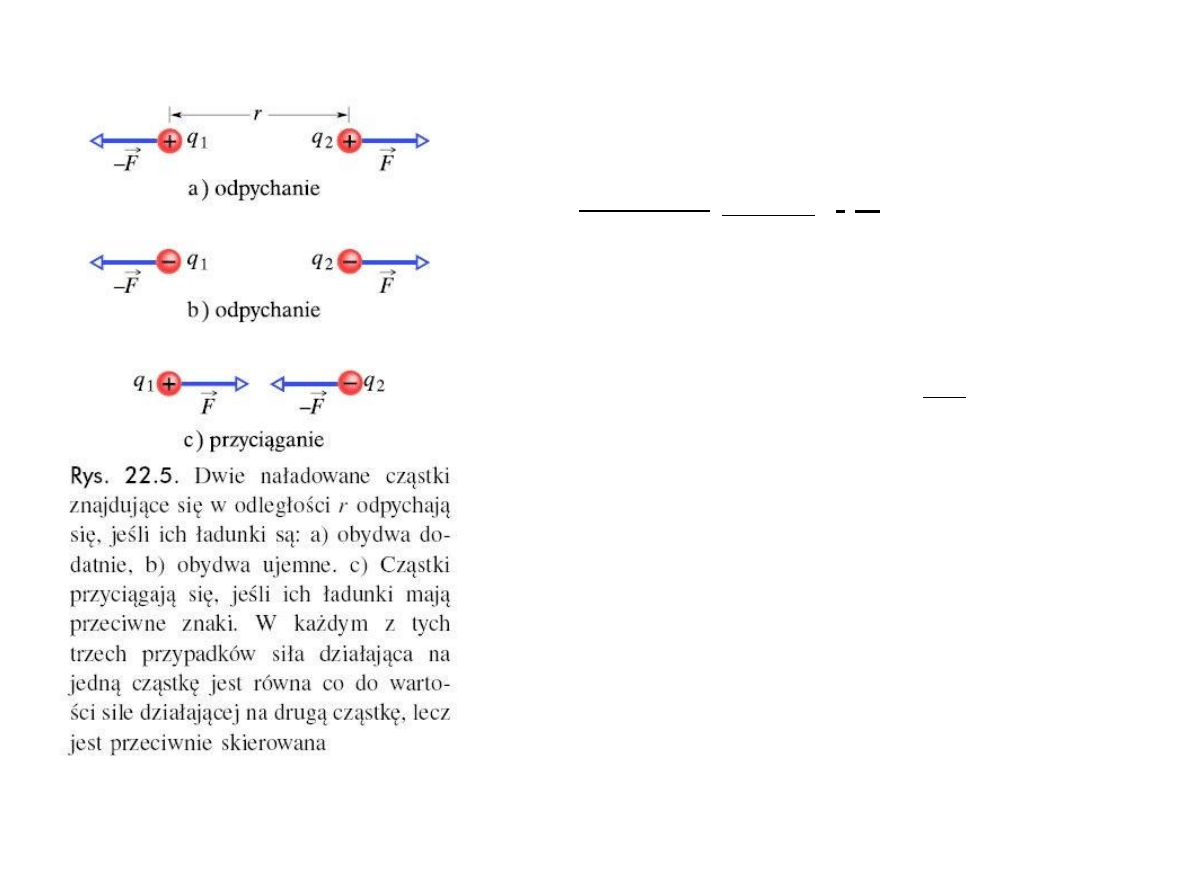
r

,



| r |

|

2



| r

4









o

1

q

1



q

2





F







(2.1.1.1)

gdzie

 



m







8.85



10



12



F



o

jest przenikalno

ścią elektryczną

pr

óżni.

Wz

ór (2.1.1.1) jest matematycznym

zapisem

prawa Coulomba

.

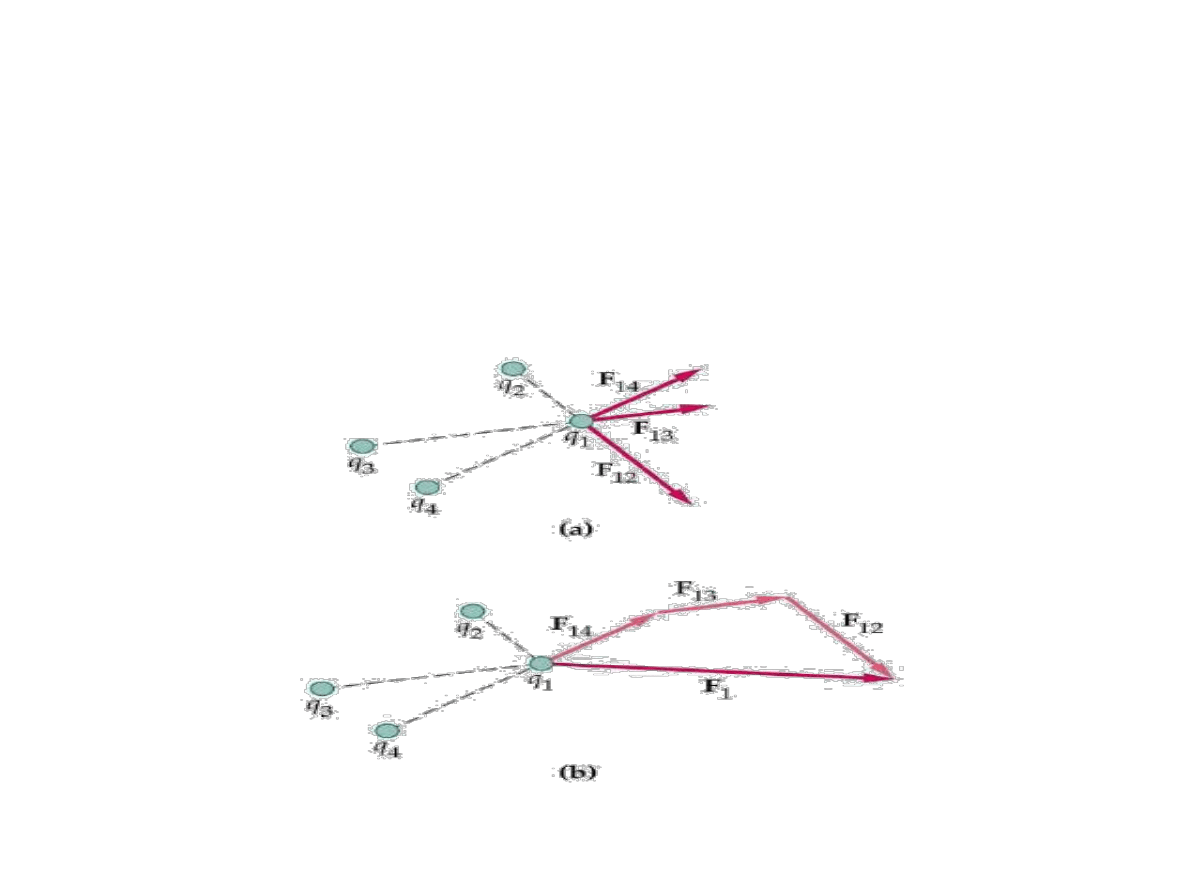
W przypadku uk

ładu więcej niż dwóch ładunków punktowych siła

dzia

łająca na jeden wyróżniony ładunek, jest równa sumie wektorowej

si

ł pochodzących od wszystkich ładunków:









F

1



F

12



F

13



...



F

1n

.

(2.1.1.2)

Ładunki elektryczne wytwarzają wokół siebie

pole elektryczne

– obszar

przestrzeni w kt

órym na umieszczone ładunki działają siły elektryczne.

Rozr

óżnia się pola fizyczne skalarne i wektorowe. W przypadku

pola

skalarnego

wielko

ść skalarna (np. temperatura) przyjmuje określoną

warto

ść w każdym punkcie przestrzeni. W przypadku

pola wektorowego

wielko

ść wektorowa (np. siła oddziaływania Culomba) przyjmuje w

k

ażdym punkcie przestrzeni wartość kierunek i zwrot.

Dla scharakteryzowania pola wprowadza si

ę pojęcie

wektora nat

ężenia

pola elektrycznego:

(2.1.1.3)



gdzie q jest

ładunkiem znajdującym się w polu elektrycznym, a

F

s

iłą z jaką pole oddziałuje na ten ładunek.

Pole elektryczne przedstawia si

ę również za pomocą

linii nat

ężenia

pola

, nazywane ta

kże

liniami s

ił

. S

ą to krzywe, do których styczne w

ka

żdym punkcie pokrywają się z kierunkiem wektora natężenia pola

elektrycznego (a wi

ęc i z kierunkiem wektora siły).

Przyk

ładowe rozkłady linii sił pola elektrycznego dla różnych rozkładów

ładunków:

E



F

,

q





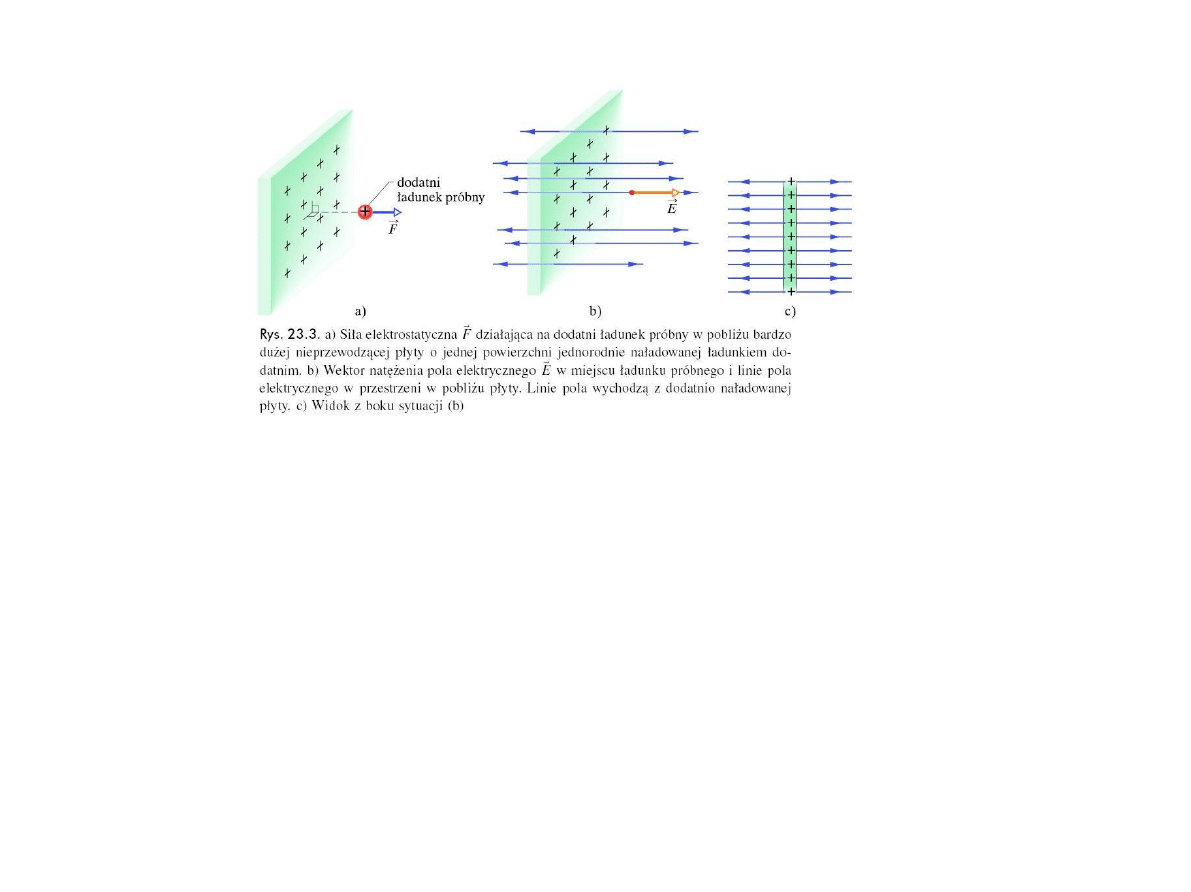
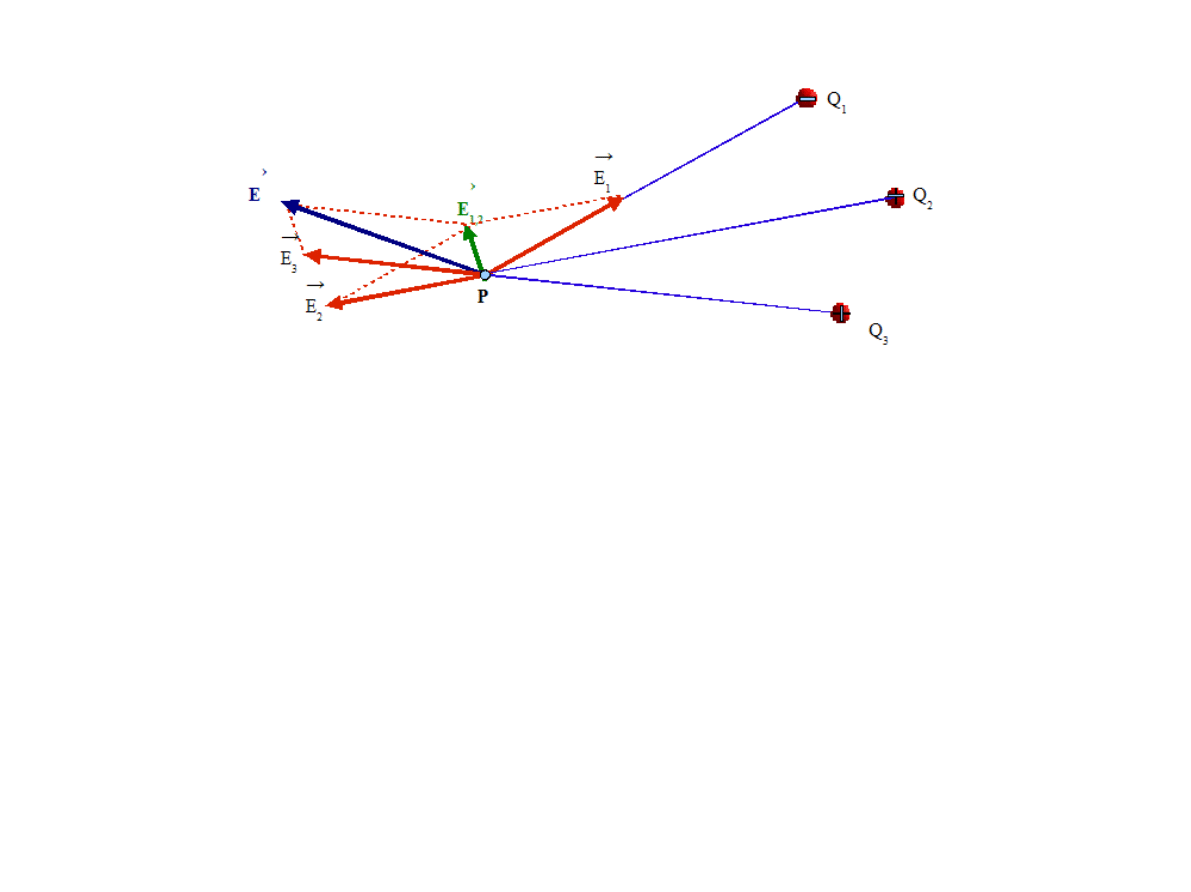
J

eżeli pole elektrostatyczne jest wytworzone przez układ Q

1

, Q

2

,

…Q

n

ładunków, to natężenia pola wypadkowego jest równe sumie
wektorowej nat

ężeń pól wytworzonych przez każdy z tych ładunków:









E



E

1



E

2



...



E

n

.

(2.1.1.4)

Pole elektrostatyczne jest polem zachowawczym (dzia

łające w nim siły

s

ą zachowawcze). Sensowne jest więc wprowadzenie dla niego energii

potencjalnej.

Energia potencjalna

ładunku punktowego jest równa pracy, jaką

wykonuj

ą siły pola , aby przenieść ładunek z danego punktu do

niesko

ńczoności.

Stosunek energii potencjalnej U

ładunku q do wartości tego ładunku

jest

potencja

łem pola elektrostatycznego

:





U

.

q

(2.1.1.5)

Potencja

ł φ jest wielkością skalarną, a jego jednostką jest wolt [V].

Je

śli pole jest wytworzone przez n ładunków punktowych

Q

1

, Q

2

,

…Q

n

, to potencja

ł w pewnym punkcie P pola

elektrostatycznego jest sum

ą potencjałów wytworzonych przez

pojedyncze

ładunki:







1





2



...





n

.

(2.1.1.6)

P







1





2





3

Q

1

Q

2



r

2

Q

3



r

1



r

3

Potencja

ł pochodzący od ładunku punktowego jest równy

,



4









o



| r

i

|



i



i

Q

(2.1.1.7)



gdzie

| r

i

|

jest odleg

łością danego ładunku od punktu, w którym

okre

ślany jest potencjał.

R

óżnica potencjałów między dwoma punktami nosi nazwę

napi

ęcia

elektrycznego

.

Opr

ócz linii pola, pole elektrostatyczne możemy przedstawić za pomocą

powierzchni ekwipotencjalnych,

czyli powierzchni o jednakowym

potencjale. Powierzchnie te s

ą prostopadłe do linii sił pola.

Powierzchnie ekwipotencjalne dla przyk

ładowych rozkładów ładunków:

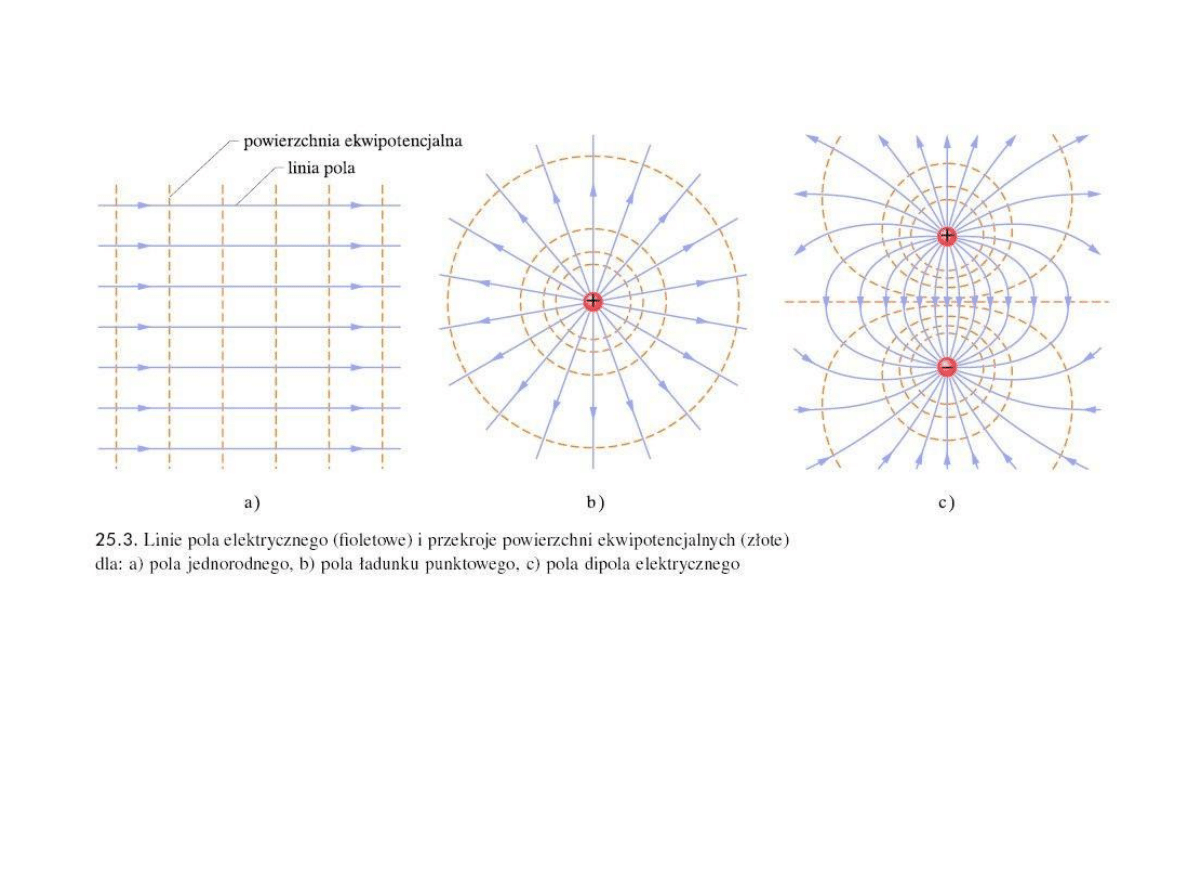
Przyk

ład (animacja): „elektro”.

Film

„Siły w polu elektrycznym” (6 min 05 s – 17min 30 s).

2.2 P

rąd elektryczny.

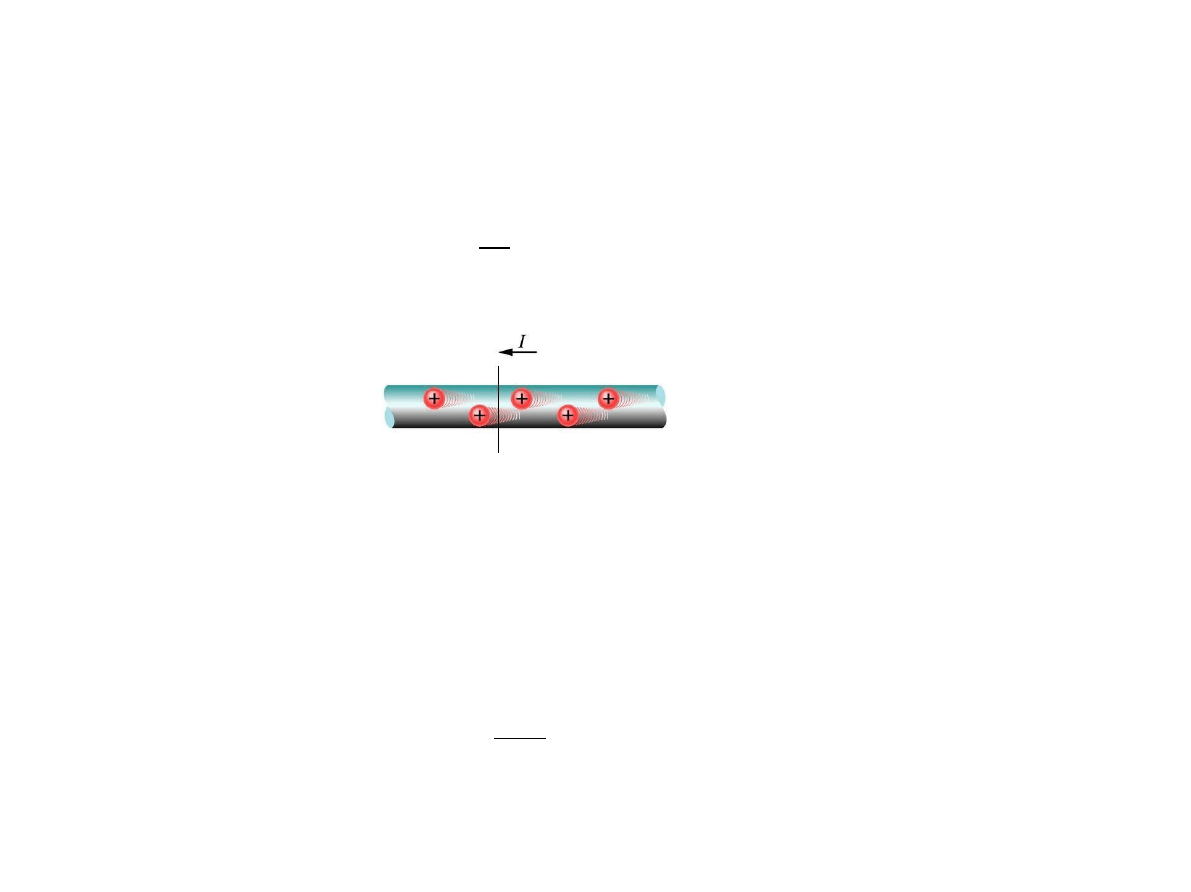
Pr

ąd elektryczny

jest uporz

ądkowanym ruchem ładunków.

Ładunki przenoszone są za pośrednictwem

no

śników ładunku

.

W metalach no

śnikami ładunków są elektrony. W półprzewodnikach

no

śnikami ujemnymi są elektrony, nośnikami dodatnimi – dziury.

W cieczach no

śnikami ładunków są jony dodatnie (kationy) i jony

ujemne (aniony). W gazach no

śnikami prądu są jony i elektrony.

Za umowny kierunek p

rądu przyjmuje się kierunek ruchu nośników

dodatnich.

Nat

ężeniem prądu I nazywamy stosunek ładunku Q przepływającego

przez dany przekr

ój poprzeczny przewodnika S do czasu przepływu t

tego

ładunku:

I



Q

.

t

(2.2.1)

Jednostk

ą natężenia prądu

jest amper [A].

Nat

ężenie prądu płynącego przez daną substancję jest równe jednemu

amperowi, j

eżeli przez jej przekrój poprzeczny w czasie jednej sekundy

prze

pływa ładunek o wartości jednego kulomba:

[ A]



[C]

.

[s]

(2.2.2)

Przep

ływ prądu w przewodniku jest wywołany działaniem pola

elektrycznego na no

śniki ładunku znajdujące się wewnątrz

przewodnika. Zale

żnie od znaku ładunków nośniki te poruszają się

zgodnie z kierunkiem pola (no

śniki dodatnie), lub przeciwnie do

kierunku pola (no

śniki ujemne). Jeżeli zatem do końców przewodnika

przy

łożone zostanie napięcie U, to wytworzone w ten sposób pole

elektryczne spowoduje prze

pływ prądu o natężeniu I. Iloraz

I

R



U

(2.2.3)

nazywamy

oporem elektrycznym

.

Jednostk

ą oporu jest om [Ω]:

[



]



[V ]

.

[ A]

(2.2.4)

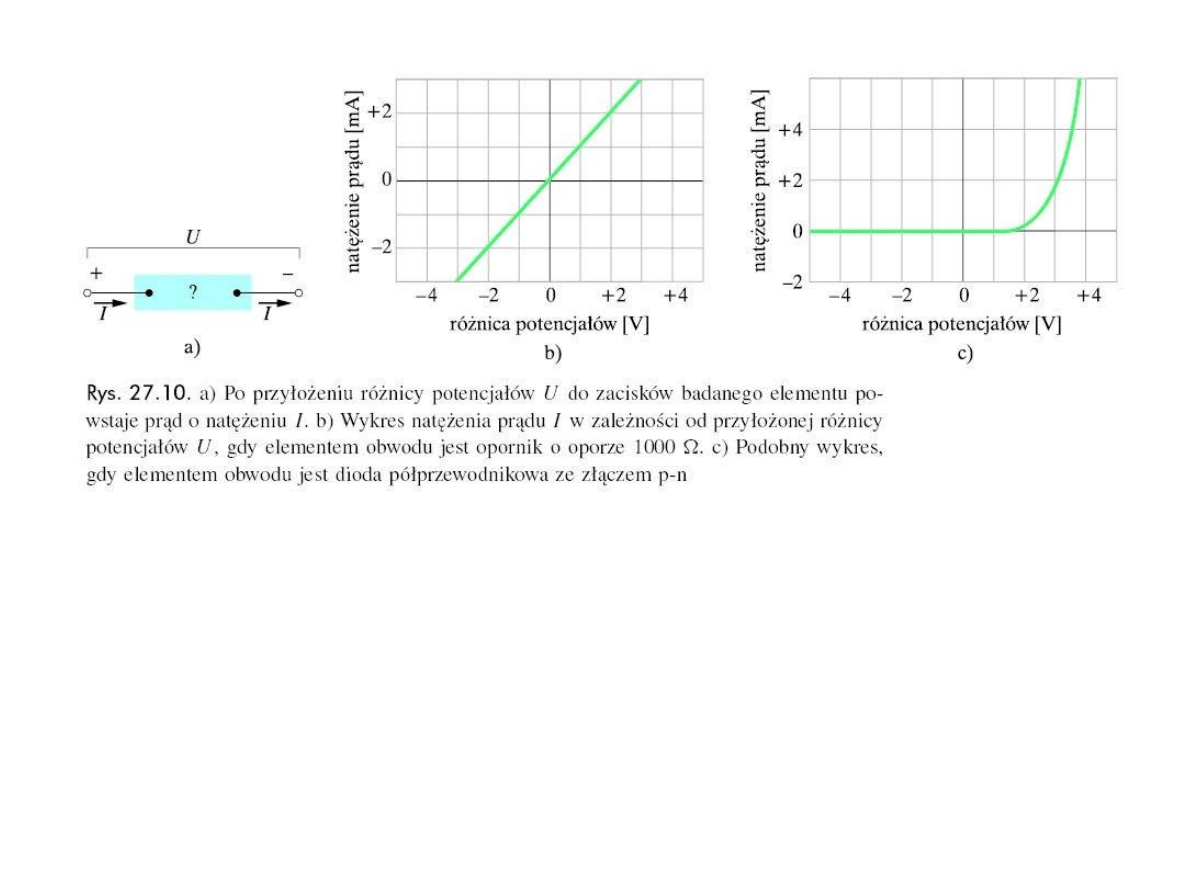
Do

świadczalnie ustalono, że stosunek napięcia między dwoma

punktami przewodnika do nat

ężenia przepływającego przez niego prądu

jest wielko

ścią stałą i nie zależy ani od napięcia, ani od natężenia prądu.

Powy

ższe twierdzenie nosi nazwę

prawa Ohma

.

Przepisuj

ąc wzór (2.2.3) w postaci

R

I



U

(2.2.5)

wnioskujemy,

że natężeniem prądu jest wprost proporcjonalne do

przy

łożonego napięcia.

Prawo Ohma jest

ściśle spełnione dla przewodników metalicznych

znajduj

ących się w stałej temperaturze.

Przyk

ład (animacja): „ohm”.

Op

ór danego przewodnika zależy od jego wymiarów. Jest on wprost

proporcjonalny do

długości l i odwrotnie proporcjonalny do przekroju

poprzecznego S przewodnika:

R







l

.

S

(2.2.6)

Wsp

ółczynnik proporcjonalności ρ we wzorze (2.2.6) nosi nazwę

oporu

właściwego

. Ze wzoru (2.2.6) wynika,

że jednostką oporu właściwego

jest [

Ω m].

Ze wzgl

ędu na opór właściwy materiały dzieli się umownie na

nast

ępujące grupy:

- metale, b

ędące bardzo dobrymi przewodnikami (ρ rzędu 10

-8

Ω m),

- p

ółprzewodniki (ρ rzędu 10

-6

Ω m),

- elektrolity (

ρ rzędu 10

-1

do 10

3

Ω m),

- izolatory (

ρ rzędu 10

10

do 10

16

Ω m).

Odwrotno

ść oporu właściwego nazywa się

przewodnictwem

właściwym

σ:

1









.

1



m





(2.2.7)