1. Układ Inercjalny, Nieinercjalny. Siła Coriolisa.

Układ inercjalny (inaczej inercyjny) - układ odniesienia, względem którego każde ciało, niepodlegające zewnętrznemu oddziaływaniu z innymi ciałami, porusza się bez przyspieszenia (tzn. ruchem jednostajnym prostoliniowym lub pozostaje w spoczynku). Istnienie takiego układu jest postulowane przez pierwszą zasadę dynamiki Newtona (zasada bezwładności: Jeśli na ciało nie działa żadna siła lub siły działające równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym).

Inercjalny układ odniesienia można również zdefiniować jako taki układ, w którym nie pojawiają się pozorne siły bezwładności. Ziemię przyjmuje się często za układ inercjalny. W rzeczywistości, układ związany z Ziemią nie jest inercjalny ponieważ w związku z jej ruchem obrotowym, na ciała materialne znajdujące się na jej powierzchni, działają siły bezwładności: siła odśrodkowa oraz siła Coriolisa. Lepszym przybliżeniem układu inercjalnego jest układ związany ze Słońcem. Ten układ z kolei, też nie jest dokładnie inercjalny, ponieważ Układ Słoneczny okrąża centrum naszej Galaktyki.

Zasada Galileusza wszystkie układy inercjalne są sobie równoważne każde zjawisko przebiega identycznie w dowolnym układzie inercjalnym. W układzie nie inercjalnym można stosować zasady dynamiki jeżeli uwzględnimy siłę unoszenia np.: siła bezwładności, odśrodkowa, Coriolisa.
Układ związany z Ziemią jest układem nieinercjalnym efektem tego jest siła Coriolisa, która działa na ciało poruszające się na powierzchni. Np.: niże na półkuli N kręcą się w lewo.

Efekt Coriolisa - efekt występujący w obracających się układach odniesienia. Dla obserwatora pozostającego w obracającym się układzie odniesienia, objawia się zakrzywieniem toru ciał poruszających się w takim układzie. Zakrzywienie to zdaje się być wywołane jakąś siłą, tak zwaną siłą Coriolisa. Siła Coriolisa jest siłą pozorną, występującą jedynie w nieinercjalnych układach, czyli takich, w których układ odniesienia porusza się ruchem niejednostajnym względem jakiegokolwiek inercjalnego układu odniesienia. Dla zewnętrznego obserwatora siła ta nie istnieje. Dla niego to układ zmienia położenie a poruszające się ciało zachowuje swój stan ruchu zgodnie z I zasadą dynamiki. Siła ta wyrażona jest wzorem:

Z siłą tą wiąże się przyspieszenie Coriolisa:

gdzie:
m - masa ciała
v - prędkość ciała
ω - prędkość kątowa układu
x- iloczyn wektorowy

Siła Coriolisa powoduje odchylenie od linii prostej toru ruchu ciała poruszającego się w układzie obracającym się. Inną siłą związana z nieinercjalnym układem odniesienia jest siła bezwładności. Jest to także pozorna siła nie pochodząca od żadnego ciała, będąca wynikiem przyspieszenia układu odniesienia (czyli układu nieinercjalnego).2. Elementy Teorii Względności

Teoria względności (Alberta Einsteina) składa się z dwóch teorii fizycznych:

1. Szczególnej teorii względności, odnoszącej się do układów inercjalnych, czyli poruszających się wobec siebie ze stałą prędkością. opublikowanej w 1905 roku.

2. Ogólnej teorii względności, Zgodnie z ogólną teorią względności, siła grawitacji wynika z lokalnej geometrii czasoprzestrzeni. Przesłanką za wprowadzeniem teorii względności była potrzeba usunięcia niezgodności między zasadą względności Galileusza głoszącej, że prędkość jest względna, a prawami elektrodynamiki. Po odkryciu przez Lorentza dylatacji czasu i skrócenia długości, Einstein zaproponował zmianę mechaniki newtonowskiej. Zmienił definicje energii i pędu, oraz transformacje Galileusza zastąpił transformacją Lorentza, w której charakterystyczna cechą jest niezależność prędkości światła od prędkości układu. Zapewniło to zgodność z obserwacjami bez zmiany elektrodynamiki ani zasady względności.

LORENTZ

Długość (kontrakcja)

Jeżeli w układzie odniesienia względem, którego ciało znajduje się w spoczynku, długość ciała jest równa l_0, to w układzie odniesienia względem którego ciało porusza się z prędkością V długość ciała będzie równa:

gdzie:
V - prędkość obiektu względem układu odniesienia
C - prędkość światła

Wymiary poprzeczne nie ulegają skróceniu, skróceniu ulega tylko wymiar równoległy do kierunku ruchu.

Czas (dylatacja)

T(tau)=Δt=t₂-t₁

Jeżeli w układzie spoczynkowym odstęp czasowy między dwoma ciałami jest równy T₀ to odstęp czasowy między tymi zjawiskami w układzie odniesienia poruszającym się z prędkością jest równy:

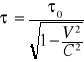
Masa

Jeżeli w układzie względem którego ciało jest w spoczynku masa ciała jest równa m₀ to w układzie odniesienia względem którego ciało porusza się z prędkością V jego masa jest równa:

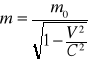
Energia

Całkowita energia ciała jest równa:

3. Zasady Dynamiki w Przypadku Klasycznym i Relatywistycznym

Zasady dynamiki Newtona - trzy zasady leżące u podstaw mechaniki klasycznej (dział mechaniki w fizyce opisujący ruch ciał (kinematyka), wpływ oddziaływań na ruch ciał (dynamika) oraz badaniem równowagi ciał materialnych (statyka)). Mechanika klasyczna oparta jest na prawach ruchu (zasadach dynamiki).

I Zasada Dynamiki (zasada bezwładności)

Jeśli na ciało nie działa żadna siła lub siły działające równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym. O takim ruchu mówimy czasem jako o ruchu swobodnym.

II Zasada Dynamiki

Jeśli siły działające na ciało nie równoważą się (czyli siła wypadkowa
jest różna od zera), to ciało porusza się z przyspieszeniem wprost proporcjonalnym do siły wypadkowej. Współczynnik proporcjonalności jest równy odwrotności masy ciała.

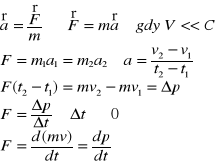
W wersji zwanej uogólnioną (uogólniona druga zasada dynamiki), zasada ta obowiązuje również dla ciała o zmiennej masie np. w mechanice relatywistycznej: Zmiana pędu ciała jest proporcjonalna do działającej siły wypadkowej.

III Zasada Dynamiki (akcji i reakcji)

Jeśli ciało A działa na ciało B siłą F (akcja), to ciało B działa na ciało A siłą (reakcja) o takiej samej wartości i kierunku, lecz o przeciwnym zwrocie.

III Zasada dynamiki, słuszna tylko w mechanice nierelatywistycznej. Zasady dynamiki mają swoje wersje także dla ruchu obrotowego (punktu i bryły) oraz mogą być stosowane w układach nieinercjalnych po uwzględnieniu sił bezwładności.

4. Podstawowe Wielkości w Ruchu Obrotowym Bryły Sztywnej

Bryła sztywna - to takie ciało, w którym pod wpływem działających sił zewnętrznych nie zmienia się wzajemna odległość pomiędzy cząsteczkami tego ciała (siły te nie zmieniają kształtu ciała).

Ruch obrotowy to taki ruch, w którym wszystkie punkty bryły sztywnej (ciało, którego elementy (części, punkty) nie mogą się względem siebie przemieszczać) poruszają się po okręgach o środkach leżących na jednej prostej zwanej osią obrotu. Np. ruch Ziemi wokół własnej osi. Jest to ruch złożony z ruchu postępowego środka masy danego ciała oraz ruchu obrotowego względem pewnej osi. Środek masy ciała można uważać za punkt materialny. Do opisania ruchu obrotowego używa się odmiennych pojęć od używanych do opisania ruchu postępowego.

Droga kątowa jest to krąg zakreślony przez promień wodzący.

Moment bezwładności I punktu materialnego o masie m znajdującego się w odległości r od osi obrotu wyraża się wzorem:

gdzie:
m - masa
r - odległość od osi obrotu

W oparciu o tę zależność można stosunkowo prosto wyliczyć moment bezwładności kilku popularnych brył:

- walca

- kuli

- pręta

gdzie:
I - moment bezwładności bryły
m - masa
r - promień
l - długość

Wszystkie powyższe wzory określają moment bezwładności brył względem osi przechodzących przez środek masy danej bryły. Do określenia momentu bezwładności względem innej osi pomocne jest Twierdzenie Steinera.

Twierdzenie Steinera

Jeżeli moment bezwładności bryły sztywnej względem osi l przechodzącej przez środek masy jest równy I₀ to moment bezwładności tej bryły względem osi l' równoległej do l odległej od niej o d jest równy:

gdzie:
I, I₀ - moment bezwładności
m - masa ciała
d - odległość między tymi osiami

Moment siły

Moment M siły działającej na ciało to wielkość wektorowa określona przez iloczyn wektorowy działającej siły i promienia.

Prędkość kątowa

Prędkość kątowa jest wektorem, który jest równoległy do osi obrotu a jego zwrot określa śruba prawoskrętna.

Prędkość kątowa obracającej się bryły to charakterystyczna dla ruchu obrotowego wielkość określająca kąt zakreślany przez bryłę w określonym czasie.

gdzie:
ω - prędkość kątowa (w rad/s, lub opuszczając radiany 1/s = s^-1)
r - promień okręgu którego fragmentem jest zakreślany łuk (najczęściej w metrach m)
V- prędkość liniowa (najczęściej w m/s)

Każdy punkt obracającej się bryły ma inną prędkość liniową, natomiast prędkość kątowa wszystkich punktów bryły jest taka sama. Punkt odległy od osi obrotu o r ma prędkość liniową v taką, że:

Przyśpieszenie kątowe

Przyśpieszenie kątowe obracającej się bryły określamy jako zmianę prędkości kątowej tej bryły w czasie.

gdzie:
dω - zmiana prędkości kątowej
dt - zmiana w czasie

Każdy punkt obracającej się bryły ma inne przyspieszenie liniowe, natomiast przyspieszenie kątowe wszystkich punktów bryły jest takie samo. Punkt odległy od osi obrotu o r ma przyspieszenie liniowe a takie, że:

gdzie:
a - przyśpieszenie liniowe
ε - przyśpieszenie kątowe
r - odległość od osi obrotu

Należy pamiętać, że wektor przyspieszenia kątowego jest prostopadły do płaszczyzny ruchu.

Pierwsza zasada dynamiki ruchu obrotowego:

W inercjalnym układzie odniesienia bryła nie obraca się lub obraca się ruchem jednostajnym (ω = const), gdy nie działają na nie żadne momenty sił lub gdy działające momenty sił się wzajemnie równoważą.

Druga zasada dynamiki ruchu obrotowego

Mówi ona, że jeśli na pewne ciało, które posiada pewien swój moment bezwładności I zadziałają zewnętrzne siły, które wywrą na to ciało pewien wypadkowy moment siły M, to w wyniku tego działania ciało będzie obracać się z przyspieszeniem kątowym ε takim, że:

gdzie:
M - moment siły
I - moment bezwładności
ε - przyśpieszenie kątowe

5. Energia Kinetyczna w Ruchu Obrotowym, Zasada Zachowania Pędu

Pęd definiujemy jako iloczyn masy i prędkości ciała.

Pęd jest wektorem o zwrocie zgodnym z kierunkiem ruchu ciała. Pęd, a raczej jego zmiana
, ma ścisły związek z siłą działającą na ciało.

Zależność tę określa się nieraz mianem uogólnionej drugiej zasady dynamiki Newtona.

Zasada zachowania pędu:

W odosobnionym układzie ciał całkowity pęd układu pozostaje stały. Przez układ odosobniony, zwany też układem zamkniętym, rozumiemy zespół ciał, pomiędzy którymi działają tylko siły wewnętrzne, czyli siły akcji i reakcji, o których mówi III zasada dynamiki. Zasada zachowania pędu obowiązuje na przykład przy zderzeniach sprężystych i niesprężystych.

Zderzenia doskonale sprężyste

W ich wyniku ciała nie odkształcają się wzajemnie, a ich energia mechaniczna przed zderzeniem i po zderzeniu pozostaje stała.

Zderzenia doskonale niesprężyste

W ich wyniku ciała odkształcają się, a część energii mechanicznej zmienia się w chwili zderzenia w energię wewnętrzną. W tym rodzaju zdarzeń nie jest spełniona zasada zachowania energii mechanicznej.

Szczególnym przypadkiem zderzeń są zderzenia centralne, czyli takie, w których wektory prędkości zderzających się ciał leżą, zarówno przed zderzeniem, jak i po zderzeniu, na jednej prostej.

Zderzenie sprężyste

Zderzenie niesprężyste

Każde obracające się ciało posiada energię kinetyczną. Energia kinetyczna obracającego się ciała jest sumą energii kinetycznych poszczególnych jego elementów.

Energia kinetyczna bryły sztywnej jest sumą energii kinetycznej jej ruchu postępowego Ekp i energii kinetycznej jej ruchu obrotowego Eko.

Prędkość v występująca we wzorze określa prędkość środka masy bryły, tak więc dla bryły, która nie przemieszcza się (np. tzw. blok nieruchomy), występuje tylko energia Eko związana z obrotem ciała. Natomiast dla np. toczącej się kuli oba te składniki mają znaczenie i wtedy całkowita energia kinetyczna Ek wynosi:

Zasada zachowania momentu pędu

Jeżeli moment sił zewnętrznych względem danej osi obrotu jest równy zeru, to moment pędu ciała (lub układu ciał) względem tej osi jest stały.

gdy M=0 to L=const. I₁ω₁=I₂ ω₂

gdzie:
I - to moment bezwładności ciała,
ω - to prędkość kątowa

6. Pole Grawitacyjne

Pole grawitacyjne to przestrzeń, w której na dowolne ciało o masie m działa przyciągająca siła grawitacyjna.

Pole grawitacyjne można zilustrować graficznie za pomocą tzw. linii sił pola. Linie te mają sens fizyczny torów, po których poruszałaby się próbna masa m umieszczona w danym punkcie pola.

Linie pola wyznaczają również w każdym punkcie pola kierunek siły wypadkowej działającej w tym punkcie na umieszczone tam ciało. Linie te nie przecinają się wzajemnie, a ich zagęszczenie jest miarą oddziaływania grawitacyjnego (większe zagęszczenie linii - silniejsze oddziaływanie).

Wyróżniamy dwa podstawowe typy pól grawitacyjnych: centralne i jednorodne.

Prawo powszechnego ciążenia

Wartość siły, z jaką oddziałują na siebie dwa ciała punktowe, jest wprost proporcjonalna do iloczynu ich mas, a odwrotnie proporcjonalna do kwadratu odległości między nimi.

Jej wartość obliczamy ze wzoru:

gdzie:
M, m - masy przyciągających się ciał,
r - odległość pomiędzy środkami tych ciał

Prawo grawitacji zapisane wektorowo:

Stała grawitacji:

Siły grawitacyjne mają zawsze charakter przyciągający i należą do tzw. oddziaływań wzajemnych. Oznacza to, że oddziaływania grawitacyjne pomiędzy dwoma dowolnymi ciałami spełniają III zasadę dynamiki Newtona.

Opis skalarny i wektorowy pola grawitacyjnego

Do opisu pola grawitacyjnego używa się takich wielkości, jak natężenie pola i potencjał grawitacyjny.

Natężenie pola
to wielkość wektorowa, definiowana jako stosunek siły
działającej na ciało o masie m, umieszczone w danym punkcie pola grawitacyjnego, do wartości masy tego ciała:

Natężenie pola ma taką samą jednostkę, jak przyspieszenie. W odróżnieniu od przyspieszenia, będącego cechą konkretnego ciała, natężenie pola jest cechą danego punktu przestrzeni, zwanej polem grawitacyjnym. Jego wartość jest jednak zawsze równa wartości przyspieszenia grawitacyjnego, z jakim porusza się ciało o masie m umieszczone w danym punkcie pola (γ = g). W polu jednorodnym wektor
ma w każdym punkcie taki sam zwrot, kierunek i wartość; w polu centralnym jego wartość maleje odwrotnie proporcjonalnie do kwadratu odległości od centrum pola, zgodnie z zależnością:

Zasada superpozycji mówi, że wypadkowe natężenie pola grawitacyjnego wytworzonego przez kilka mas punktowych w danym punkcie pola jest równe wektorowej sumie natężeń wytworzonych przez każdą z mas z osobna.

Linie sił pola grawitacyjnego wskazują w przestrzeni wokół źródła kierunek siły grawitacji jaka zadziała na ciało m umieszczone w danym polu.

Przyśpieszenie w polu grawitacyjnym

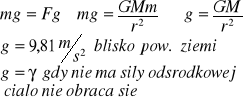
W przykładzie przedstawionym na rysunku poniżej wypadkowe natężenie pola w punkcie A wynosi:

Potencjał grawitacyjny V jest wielkością skalarną definiowaną jako stosunek energii potencjalnej Ep, jaką posiada ciało o masie m umieszczone w danym punkcie pola grawitacyjnego, do wartości tej masy.

W polu centralnym potencjał grawitacyjny obliczamy ze wzoru:

gdzie:
M - masa źródła pola
r - odległość od środka masy źródła.

Potencjał danego punktu pola, wytworzonego przez kilka mas, jest równy algebraicznej sumie potencjałów pochodzących od każdej z mas z osobna. W przykładzie przedstawionym na rysunku:

7. Prawa Keplera

Kepler, odnosząc się do heliocentrycznego układu planet (słońce układem odniesienia do poruszających się planet), jaki został zaprezentowany przez Mikołaja Kopernika oraz na podstawie długoletnich obserwacji sformułował trzy prawa, opisujące ruch planet wokół słońca:

Pierwsze Prawo Keplera:

Wszystkie planety poruszają się po orbitach eliptycznych. Słońce znajduje się w jednym z dwóch ognisk elipsy (na ogół elipsy te mało różnią się od okręgów).

P - perychelium (pkt. najbliższy słońcu,) A - adchelium (pkt. najdalej oddalony od słońca)

I uogólnione prawo Keplera - wszystkie ciała niebieskie poruszają się po krzywych stożkowych. W ogniskach tych krzywych znajduje się gwiazda.

Drugie prawo Keplera:

Odcinek prostej łączącej środek planety ze środkiem Słońca zakreśla w jednakowych odstępach czasu jednakowe pola. (wynika z tego, że prędkość planety rośnie gdy zbliża się do Słońca - największa jest w peryhelium),a najmniejsza w aphelium.

- pole zakreślone przez krążącą planetę

- przyrost drogi w czasie

II uogólnione prawo Keplera- moment pędu planety jest stały. Pęd to iloczyn masy i prędkości planety.

p=mV

Trzecie Prawo Keplera:

Nawiązuje do związku między rozmiarami planet a ich okresem obiegu wokół Słońca:
Drugie potęgi okresów T obiegu Słońca są proporcjonalne do trzecich potęg ich wielkich półosi a.

T₁,T₂ - okresy obiegu dwóch planet
a₁,a₂ - średnie odległości tych planet od słońca

III uzgodnione prawo Keplera - wszystkie ciała układu słonecznego poruszają się po elipsach wokół wspólnego środka masy

gdzie:
a - średnia odległość danej planety od Słońca
G - stała grawitacji
m - masa danej planety
M_S - masa Słońca

Czwarte „prawo” Keplera

W rzeczywistości Kepler sformułował cztery prawa opisujące ruch planet, jednak według współczesnej metodologii naukowej czwarte obecnie nie jest prawem, a jedynie ciekawą zbieżnością.

Kepler stwierdził, że jeśli na sferze wyznaczonej przez orbitę Merkurego (która w dobrym przybliżeniu jest okręgiem) opiszemy ośmiościan foremny, to okaże się, że jest on wpisany w analogiczną sferę Wenus. Jeśli na tej sferze opiszemy dwudziestościan foremny, to będzie on wpisany w sferę Ziemi; kolejny dwunastościan foremny wpisany jest w sferę Marsa, czworościan foremny opisany na niej wpisany jest w sferę Jowisza, a opisany na niej sześcian wpisany jest w sferę Saturna.

8. Ruch Harmoniczny

Ruch harmoniczny- drgania opisane funkcją harmoniczną (sinusoidalną), jest to najprostszy w opisie matematycznym rodzaj drgań.

Ruch harmoniczny - ruch w którym przyśpieszenie jest wprost proporcjonalne do wychylenia i skierowane do położenia równowagi.

gdzie:
x - wychylenie drgającego ciała z położenia równowagi
A - amplituda, czyli maksymalne wychylenie drgającego ciała z położenia równowagi, czyli po prostu maksymalna wartość x
ω - częstość kołowa drgań
t - czas
φ - faza początkowa drgań, czyli kąt, określający wychylenie ciała w chwili t=0

- wyrażenie to nosi nazwę fazy drgań
f - częstotliwość drgań /ilość drgań w 1s/
T - okres drgań /czas 1 drgania/

Ruch harmoniczny jest często spotykanym rodzajem drgań, wiele rodzajów jest w przybliżeniu harmoniczna. Każde drganie można przedstawić jako sumę drgań harmonicznych.

Przykłady ruchów harmonicznych: wahadło matematyczne, wahadło fizyczne, ciężarek na sprężynie, drgania atomów sieci krystalicznej.

Podczas drgań harmonicznych następuje ciągła przemiana Ek w Ep i odwrotnie, jednak suma tych energii pozostaje stała.

9. Drgania Tłumione, Energia Drgań

Drgania są to procesy fizyczne w których dana wielkość na przemian rośnie i maleje.

W przyrodzie zawsze występują siły tarcia, które zmniejszają energię drgań, dlatego w realnym ośrodku występują drgania tłumione a nie harmoniczne:

gdzie:

x - wychylenie drgającego ciała z położenia równowagi
β - współczynnik tłumienia
ω - częstość drgań
t - czas
φ - faza początkowa drgań

- nazywamy amplitudą drgań tłumionych (gasnących)

- wyrażenie to nosi nazwę fazy drgań

Aby otrzymać drgania harmoniczne (o stałej amplitudzie) trzeba uzupełniać zmiany energii w każdym okresie.

Energia drgań w ruchu harmonicznym:

gdzie:

A - amplituda drgań
E - energia całkowita
k - współczynnik sprężystości

Zależność wychylenia x od czasu dla drgań tłumionych przedstawiona została na rysunku:

Energia drgań w drganiach tłumionych zmniejsza się.

10. Wahadło Fizyczne i Matematyczne

Wahadło - ciało stałe zawieszone ponad swoim środkiem ciężkości, wykonujące drgania (wahania) pod wpływem siły grawitacyjnej. Wyróżnia się: wahadło matematyczne i wahadło fizyczne.

Wahadło fizyczne to ciało sztywne wykonujące wahania wokół poziomej osi zawieszenia przechodzącej przez nie. Jego drgania są również w przybliżeniu harmoniczne, o okresie:

gdzie:
I - moment bezwładności ciała względem osi obrotu,
l - odległość od punktu zawieszenia do środka ciężkości,
g - przyspieszenie ziemskie
m - masa ciała

Wahadło matematyczne

Szczególnym przypadkiem wahadła fizycznego jest wahadło matematyczne.

Wahadło matematyczne to punktowy ciężar zawieszony na nierozciągliwej, bez masowej nici o długości l. W przypadku małych drgań wahadła matematycznego drgania są w przybliżeniu harmoniczne, ich okres wyraża wzór:

gdzie:
T - okres drgań
l - długość nici
g - przyśpieszenie ziemskie

11. Pole Elektrostatyczne

Pole elektrostatyczne to przestrzeń wokół nieruchomych ładunków lub ciał naelektryzowanych, w której na ładunki elektryczne działają siły. Ładunki oznaczamy symbolami Q lub q. Jednostką ładunku elektrycznego jest 1 kulomb [1C].

Pole elektrostatyczne przedstawia się graficznie za pomocą tzw. linii pola. Linie pola mają sens fizyczny torów, po których poruszałby się w danym polu mały próbny ładunek dodatni. Linie pola zawsze zaczynają się na ładunkach dodatnich, a kończą na ujemnych. Linie pola wyznaczają również w każdym punkcie pola kierunek siły wypadkowej działającej na ciało, obarczone ładunkiem, umieszczone w tym punkcie. Linie te nie przecinają się wzajemnie, a ich zagęszczenie jest miarą oddziaływania elektrostatycznego (większe zagęszczenie linii - silniejsze oddziaływanie).

Wyróżniamy dwa podstawowe typy pól elektrostatycznych: centralne i jednorodne.

Rysunki przedstawiają linie kilku rodzajów pola elektrostatycznego:

Prawo Coulomba

Wartość siły, z jaką oddziałują na siebie dwa punktowe ładunki elektryczne, jest wprost proporcjonalna do iloczynu tych ładunków, a odwrotnie proporcjonalna do kwadratu odległości między ich środkami. Jej wartość obliczamy ze wzoru:

gdzie:
F - siła wzajemnego oddziaływania dwóch punktowych ładunków elektrycznych
Q, q - punktowe ładunki elektryczne
r - odległość pomiędzy ładunkami
k - współczynnik proporcjonalności

gdzie:

- względna przenikalność elektryczna ośrodka

- przenikalność elektryczna próżni

Dwa ładunki różnoimienne przyciągają się, dwa jednoimienne odpychają się wzajemnie.

Gęstość powierzchniowa ładunku σ to stosunek ładunku Q zgromadzonego na powierzchni przewodnika do wartości tej powierzchni:

gdzie:
q - ładunek elektryczny
S - powierzchnia na którą rozłożony jest ładunek

W przewodniku metalowym ładunek gromadzi się tylko na jego powierzchni, przy czym gęstość σ jest tym większa, im mniejszy jest promień krzywizny powierzchni. Oznacza to, że na końcach ostrych nagromadzenie ładunku jest większe niż na powierzchniach płaskich.

Opis skalarny i wektorowy pola elektrostatycznego

Do opisu pola elektrostatycznego używa się takich wielkości, jak natężenie pola i potencjał.

Natężenie pola
to wielkość wektorowa, definiowana jako stosunek siły
działającej na dany ładunek q, umieszczony w danym punkcie pola elektrostatycznego, do wartości tego ładunku:

gdzie:

- natężenie pola

- siła działająca na ładunek q
q - wartość ładunku umieszczonego w danym pkt pola elektro.

Wektor natężenia pola
jest zawsze skierowany zgodnie z liniami pola elektrostatycznego i w danym punkcie pola jest styczny do linii pola.

W polu jednorodnym wektor
ma w każdym punkcie taki sam zwrot, kierunek i wartość. W polu centralnym jego wartość maleje odwrotnie proporcjonalnie do kwadratu odległości od centrum pola, zgodnie z zależnością:

Zasada superpozycji mówi, że wypadkowe natężenie pola elektrostatycznego wytworzonego przez kilka ładunków punktowych w danym punkcie pola jest równe wektorowej sumie natężeń wytworzonych przez każdy z ładunków z osobna. W przykładzie przedstawionym na rysunku:

Potencjał elektrostatyczny V jest wielkością skalarną definiowaną jako stosunek energii potencjalnej Ep, jaką posiada ładunek q, umieszczony w danym punkcie pola, do wartości tego ładunku.

Prawo Gaussa dla pola elektrostatycznego

Strumień natężenia pola elektrostatycznego Φ przechodzący przez dowolną powierzchnię zamkniętą jest równy całkowitemu ładunkowi zawartemu wewnątrz tej powierzchni podzielonemu przez stałą dielektryczną próżni
.

gdzie:
Sγ - powierzchnia Gaussa

- stała dielektryczna próżni
Q - całkowity ładunek zawarty wewnątrz powierzchni

Prawo Gaussa umożliwia obliczanie natężeń pól elektrostatycznych wytworzonych przez ładunki, których rozkład w przestrzeni jest symetryczny, np. ładunki na powłoce kulistej, na powierzchni walca.

12. Praca w Polu Elektrycznym, Potencjał, Rozmieszczenie Ładunków Na Przewodniku. Potencjał elektryczny

Praca w polu elektrycznym jest polem zachowawczym ponieważ praca w tym polu nie zależy od drogi tylko od różnicy potencjałów.

Praca równa jest różnicy energii potencjalnej między dwoma punktami:

Różnicę potencjałów między dwoma punktami pola nazywamy napięciem elektrycznym U.

Więc:
Praca w polu elektrycznym jest równa iloczynowi napięcia i wartości przenoszonego ładunku.

gdzie:
W - praca wpolu elektrycznym
q - ładunek
V₁,V₂ - potencjały elektryczne
U - napięcie elektryczne

Potencjał pola elektrycznego w danym pkt. nazywamy pracę którą wykona pole dla przesunięcia ładunku jednostkowego z tego pkt. do nieskończoności albo jest to stosunek energii potencjalnej jaką ma ład. w tym pkt. do jego wartości.

gdzie:
V - potencjał pola elektrycznego
E_p - energia potencjalna
q - ładunek

Jednostką potencjału jest 1 V (wolt) 1 V =

Energia potencjalna dwóch ładunków wyrażona jest wzorem:

gdzie:
Q - wartość ładunku źródła pola,
q - wartość ładunku próbnego
R - odległość między ładunkami
k - współczynnik proporcjonalności (stała Coulomba) (w próżni k=9*10⁹ [N*m²/C²]

Przekształcając odpowiednio oba powyższe wzory otrzymujemy wzór na potencjał elektryczny w postaci:

Potencjał w danym punkcie pola zależy od wartości ładunku źródła pola oraz od odległości tego punktu od źródła pola.

Rozkład ładunku na powierzchni przewodnika Ładunek wprowadzony na przewodnik gromadzi się na jego powierzchni. Ładunki na powierzchni kuli rozkładają się równomiernie. Na innych powierzchniach rozkład ładunku nie jest równomierny. Najwięcej ładunków mieści się na powierzchniach o małej krzywiźnie.

Rozkład ładunku na powierzchni przewodnika charakteryzuje pojęcie średniej gęstości ładunku.

gdzie:

- średnia gęstość ładunku
q - wartość zgromadzonego ładunku
S - powierzchnia

Średnią gęstością powierzchniową ładunku nazywamy stosunek zgromadzonego na powierzchni ładunku do pola tej powierzchni.

Jednostką gęstości jest 1 C / m2.

Szczególnie duża jest gęstość powierzchniowa ładunku na wszelkiego rodzaju ostrzach.

Rozmieszczenie ładunków na przewodniku

Gęstość powierzchniowa, której jednostką jest kulomb na metr kwadratowy

gdzie:

- gęstość powierzchniowa
q - ładunek elektryczny
S - powierzchnia, na której rozłożony jest ładunek

Gęstość objętościowa (lub tylko gęstość), której jednostką jest kulomb na metr sześcienny

gdzie:

- gęstość
V - objętość zajmowana przez ładunek

Gęstość liniowa, której jednostką jest kulomb na metr

gdzie:

- gęstość liniowa
l - długość (np. pręta, nitki), na której rozłożony jest ładunek

Ładunek gromadzi się na zewnętrznej powierzchni przewodnika.

13. Pojemność Elektryczna i Kondesatory

Kondensator to układ dwóch przewodników rozdzielonych próżnią bądź dielektrykiem. Kondensator płaski tworzą dwie równoległe płytki przewodzące (okładki), umieszczone w niewielkiej odległości d od siebie. Okładki naładują się ładunkami +Q i -Q równymi co wartości bezwzględnej, lecz o przeciwnych znakach.

Natężenie E jednorodnego pola elektrycznego wewnątrz naładowanego do napięcia U kondensatora jest równe:

d - odległość między okładkami

Natężenie pola elektrostatycznego w kondensatorze próżniowym można wyrazić przez gęstość ładunku zgromadzonego na powierzchni S okładki
z prawa Gaussa:

Pojemność kondensatora

Kondensator charakteryzuje pojemność określająca zdolność kondensatora do gromadzenia ładunku:

gdzie:
C - pojemność, w faradach
Q - ładunek zgromadzony na jednej okładce, w kulombach
U - napięcie elektryczne między okładkami, w woltach

Pojemność kondensatora płaskiego C zależy od jego rozmiarów geometrycznych (S i d) oraz od rodzaju dielektryka wypełniającego kondensator
i wyraża się wzorem:

gdzie:
S - powierzchnia czynna płytki
d - odległość między płytkami

- przenikalność elektryczna

- przenikalność elektryczna próżni
C - jest to podstawowy parametr kondensatora

Pojemność kondensatora C nie zależy ani od ładunku Q na jego okładkach, ani od napięcia U między nimi.

Ładunkiem Q

Nazywamy wartość bezwzględną ładunku na jednej z okładek kondensatora. Ładunek zgromadzony na okładkach kondensatora jest wprost proporcjonalny do napięcia między jego okładkami:

Do kondensatorów nie można podłączyć dowolnie dużych napięć, gdyż może nastąpić trwałe ich uszkodzenie w wyniku przebicia między okładkami.

Kondensatory o różnych pojemnościach C1, C2, podłączone do tego samego napięcia U naładują się ładunkami proporcjonalnymi do ich pojemności.

W układzie SI jednostką pojemności jest Farad [F]. Pojemność 1 F jest bardzo duża, dlatego częściej stosuje się mniejsze jednostki, np. mikrofarad 1µF=10^-6F.

14. Prąd elektryczny

Prąd elektryczny - uporządkowany ruch ładunków elektrycznych (dodatnich lub ujemnych) zwanych nośnikami prądu.

Prąd stały - w odróżnieniu od prądu zmiennego i przemiennego - prąd stały charakteryzuje się stałą wartością natężenia oraz kierunkiem przepływu. Zaletą prądu stałego jest to, że w przypadku zasilania takim prądem wartość chwilowa dostarczanej mocy jest stała, co ma duże znaczenie dla wszelkich układów wzmacniania i przetwarzania sygnałów.

Praca prądu elektrycznego stałego

gdzie:
W - praca
R- opór
U - różnica potencjałów(napięcie)
T - czas przepływu
I - natężenie
Q - całkowity ładunek, który przepłynął

Moc prądu elektrycznego stałego:

gdzie:
P - moc,
W - praca
T - czas wykonywania pracy
U - różnica potencjałów (napięcie),
I - natężenie

Z powyższego równania wynika zatem, że tę samą moc (a więc i energię) można przesłać przy różnych wartościach napięcia i prądu.

Natężenie prądu I - Jest to stosunek ładunku ΔQ przepływającego przez poprzeczny przekrój przewodnika do czasu jego przepływu Δt:

gdzie:
I - natężenie prądu

- ilość ładunku

- przedział czasu

Jeżeli natężenie prądu nie ulega zmianie w czasie to prąd taki nazywamy prądem stałym.

Prawo Ohma -Natężenie prądu zależy wprost proporcjonalnie od napięcia:

gdzie:
R - opór
U - różnica potencjałów(napięcie)
I - natężenie prądu

Współczynnik proporcjonalności G nazywa się przewodnością przewodnika.
Wartość odwrotna do przewodności to opór R.

Opór przewodnika - dla jednorodnego przewodnika cylindrycznego jego opór R jest wprost prop. do jego długości a odwrotnie prop. do pow. przekroju poprzecznego.

gdzie:
l - długość elementu
S - pole przekroju poprzecznego elementu
ρ - rezystywność materiału

Siła elektromotoryczna (SEM) - Miarą SEM ogniwa jest różnica potencjałów między elektrodami gdy nie czerpiemy prądu elektrycznego:

gdzie:
W - praca

- siła elektromotoryczna ogniwa
Q - ładunek jednostkowy

I prawo Kirchhoffa - Suma natężeń prądów dopływających do węzła jest równa sumie natężeń prądów wypływających z tego węzła.

Przyjmuje się konwencję, że prądy zwrócone do węzła mają znak (+), zaś prądy ze zwrotem od węzła mają znak (-), np.:

II prawo Kirchhoffa można sformułować na kilka sposobów. Oto pierwszy z nich:

W obwodzie zamkniętym suma spadków napięć na wszystkich odbiornikach prądu musi być równa sumie napięć na źródłach napięcia.

Jeśli napięcie na źródle oznaczymy U_E, a napięcia na opornikach odpowiednio U₁ i U₂, to prawdziwy będzie związek: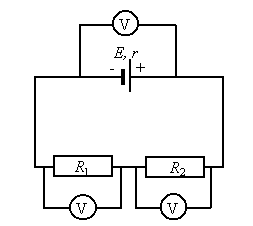

W „oczkowym” sformułowaniu II prawo Kirchhoffa będzie miało postać:

W oczku prąd suma spadków napięć na wszystkich odbiornikach prądu musi być równa zeru.

Można to zapisać wzorem:

15. Pole Magnetyczne

Magnesy naturalne oraz przewodniki z prądem wytwarzają w otaczającej je przestrzeni pole magnetyczne. Pole magnetyczne działa siłą tylko na ładunki będące w ruchu, a więc na pojedyncze swobodnie poruszające się ładunki, np. elektrony, protony, cząstki α, a także na przewodniki z prądem.

Pole magnetyczne przestrzeń, w której na biegunie magnetycznym działa siła, biegunów nie da się rozdzielić.

Prawo Gausa dla magnetyzmu mówi, że:

Całkowity strumień pola magnetycznego przez dowolną powierzchnię zamkniętą równy jest zeru. Oznacza to, że nie istnieją ładunki magnetyczne.

Stałe pole magnetyczne nie działa na ładunki nieruchome oraz na ładunki poruszające się równolegle do linii indukcji magnetycznej (v||B).

Indukcja magnetyczna

Wielkość wektorowa opisująca pole magnetyczne. Wektor ten określa siłę Lorentza, z jaką pole magnetyczne działa na poruszający się w nim ładunek elektryczny.

Siła Lorentza - Jest to siła działająca na cząstki naładowane poruszające się w polu magnetycznym. Siłę Lorentza działającą na ładunek q poruszający się z V w polu magnetycznym o indukcji B wyznacza się ze wzoru:

gdzie:
q - ładunek
v - prędkość z jaką porusza się ładunek
B - indukcja magnetyczna

jej wartość wynosi:

gdzie:
F_L - siła Lorentza
q - ładunek ciała (skalar)
v - prędkość ciała (wektor)
B - indukcja magnetyczna (wektor)

- kąt pomiędzy wektorem prędkości a indukcji magnetycznej

jej kierunek i zwrot określa się regułą lewej dłoni

Siła Lorentza nie zmienia energii kinetycznej cząstki, gdyż nie wykonuje pracy. (F_L┴ v). Pod wpływem siły Lorentza zmienia się tylko kierunek ruchu cząstki naładowanej, a wartość prędkości pozostaje stała.

Jednostką indukcji magnetycznej jest tesla (T).

Pole magnetyczne prądu elektrycznego

Oersted odkrył: przewodnik z prądem wytwarza pole magnetyczne, linie sił tego pola są okręgami współśrodkowymi z tym przewodnikiem.

Natężenie pola magnetycznego wokół przewodnika ma wartość:

pole mag. przewodnika prostoliniowego niesk. długiego

pole mag przewodnika kołowego

Siła elektrodynamiczna jest to siła, która działa na przewodnik elektryczny przez który płynie prąd elektryczny, umieszczony w polu magnetycznym.

Na umieszczony prostopadle w polu magnetycznym przewodnik o długości l, przez który płynie prąd o natężeniu I, działa siła magnetyczna (elektrodynamiczna) F, której wartość określa wzór:

gdzie:
l - długość przewodnika
I - natężenie prądu
B - indukcja magnetyczna

-kąt między kierunkiem przepływu prądu a kierunkiem linii pola

- zapis wektorowy

16. Falowa i Kwantowa Teoria Światła

Teoria falowa

Światło jest falą elektromagnetyczną. wyjania ona zjawiska odbicia, załamania światła, ugięcia, interferencji, polaryzacji

1. Interferencja- jest to zjawisko nakładania się fal świetlnych. Zjawisko to potwierdza falową naturę światła. Zjawisko to po raz pierwszy zaobserwował Thomas Young w roku 1802.

2. Dyfrakcja - Dyfrakcja fali jest to ugięcie się fali świetlnych na krawędziach albo szczelinach.

Przykład dyfrakcji można zobaczyć codziennie gdy się obserwuje swój cień. Cień nigdy nie jest ostry gdyż jest zawsze zamazany wzdłuż krawędzi. Jeśli światło byłoby cząstka a nie fala to rozchodziłoby się po linii prostej i wtedy krawędzie cienia byłyby ostre.

3. Polaryzacja - dotyczy wyłącznie fal poprzecznych i polega na uporządkowaniu drgań ośrodka. Światło jest falą elektromagnetyczną więc ma charakter fali poprzecznej. Kierunek polaryzacji fali elektromagnetycznych jest taki jak kierunek pola elektrycznego E^→ (przez płaszczyznę polaryzacji należy rozumieć płaszczyznę zawierającą wektor E oraz kierunek rozchodzenia się fali).

Światło może być spolaryzowane:
a)liniowo- drgania pola elektrycznego odbywają się tylko w jednym kierunku
b)kołowo- kierunek drgań obraca się cyklicznie.

Polaryzacja światła zachodzi podczas:
- załamania
- rozproszenia
- odbicia

Teoria korpuskularna

Światło jest strumieniem cząstek wyjaśnia zjawisko prostoliniowości rozchodzenia się światła, odbicia światła, Nowoczesna teoria korpuskularna to teoria kwantowa - światło strumieniem fotonów albo kwantów

Zjawisko fotoelektryczne

Kwantowe własności światła - Dowodem na kwantową naturę światła jest zjawisko fotoelektryczne. Polega ono na wybiciu elektronu przez foton z powierzchni metalu. Tego zjawiska nie można wytłumaczyć przyjmując że światło jest falą, wyjaśnia to teoria kwantowa.

gdzie
E - energia
h - stała Planca h= 6,63x10^-34Js,
f - częstotliwość
C- prędkość światła

- długość fali

Foton świetlny o zderza się z elektronem na powierzchni metalu i oddaje mu całą swoją energię, cześć tej energii zostaje zużyta na wyrwanie elektronu z pow. metalu, jest to tzw. praca wyjścia W pozostała część energii nadaje prędkość początkową, czyli zamienia się w energie kinetyczną elektronu. Aby zjawisko mogło zaistnieć energia fotonu musi być przynajmniej równa pracy wyjścia:

Hipoteza de Broglie'a

Każda cząstka posiadająca m i poruszająca się z prędkością v może być traktowana jako fala. Czyli coś co jest uważane za cząstkę np. elektron w pewnych warunkach będzie okazywać własności falowe (dyfrakcja, interferencja, polaryzacja). Przez analogie z fotonami DeB przyjął, że długość fali związanej z cząstką powinna wynosić

gdzie
p- pęd cząstki,
m-masa cząstki
v- prędkość cząstki
h - stała Planca

Dowodem na to, że fale materii istnieją jest np. dyfrakcja elektronów. Wiązka elektronów po przejściu przez warstwę grafitu tworzy obraz dyfrakcyjny.

17. Budowa jądra atomu

Jądro składa się z protonów i neutronów.

gdzie:
Z - liczba porządkowa, atomowa, liczba protonów
A - liczba protonów + neutronów

Izotopy - atomy tego samego pierwiastka o różnej liczbie masowej.
Izotopy wodoru:
- wodór
- 1proton, 0neutronów
- deuter
- 1proton, 1neutron
- tryt
- 1proton, 2neutrony

Izotopy ma również tlen (16,17,18), węgiel i inne pierwiastki.

Izotony - atomy różnych pierwiastków o takiej samej liczbie neutronów, lecz różnej liczbie masowej, np.

Izobary - atomy różnych pierwiastków o tej samej liczbie masowej, np.

Modele budowy atomu

Model atomu wg Daltona z 1808 r.

Materia zbudowana jest z kulistych atomów o równomiernie rozłożonej masie i doskonale elastycznych. Atomy danego pierwiastka mają identyczne rozmiary i masy, natomiast atomy różnych pierwiastków różnią się między sobą. W trakcie reakcji chemicznych atomy nie ulegają zniszczeniu, ani nie powstają nowe atomy.

Model atomu Thomsona (model rodzynkowy) z 1904 r.

Atom zbudowany jest z jednorodnie rozmieszczonej, dodatnio naładowanej masy o małej gęstości. W masie tej „poutykane” są ujemnie naładowane elektrony (jak rodzynki w cieście drożdżowym), tak że atom jako całość pozostaje elektrycznie obojętny.

Model atomu Rutherforda (model planetarny) z 1911 r.

Atom składa się z jądra atomowego i powłoki elektronowej. Jądro o dodatnim ładunku skupia w sobie prawie całą masę atomu, mimo że rozmiar jądra jest bardzo mały (rzędu 10^-15 m). Pomiędzy elektronami a jądrem działa siła dośrodkowa (siła kulombowska). Ładunek całkowity elektronów jest równy ładunkowi jądra (co do wartości bezwzględnej), tak że atom jako całość pozostaje elektrycznie obojętny. Pomiędzy jądrem a powłoką występuje próżnia wypełniona polem elektromagnetycznym.

Model atomu wodoru Bohra - opiera się na następujących postulatach:

a) Elektron krąży po orbicie kołowej wokół jądra, nie wypromieniowując energii.

b) Elektron może krążyć tylko po takiej orbicie, dla której spełniony jest warunek

gdzie:
K = mvr - moment pędu elektronu,
h - stała Plancka,
n - liczba naturalna (numer dozwolonej orbity elektronu)

c) Aby elektron mógł przejść z orbity niższej k na orbitę wyższą n, musi zabsorbować kwant energii o wartości E_n - E_k

d) Jeżeli elektron przeskakuje z orbity wyższej n na orbitę niższą k, to emituje przy tym kwant promieniowania o energii

hf = E_n - E_k

gdzie:
E_n, E_k - energia elektronu na orbicie n i k,
f - częstotliwość emitowanego promieniowania

Wady i zalety modelu Bohra

Model Bohra bardzo dobrze tłumaczył widmo liniowe atomu wodoru, a promień atomu obliczony na podstawie jego teorii był zgodny z teorią kinetyczną gazu.

Wadą modelu Bohra jest jego ograniczone zastosowanie (tylko dla atomów jedno elektronowych) oraz sprzeczność postulatu o niewypromieniowywaniu energii przez elektron z elektrodynamiką.

Model współczesny (kwantowy) atomu

Wokół dodatniego jądra krąży chmura elektronów, których położenie nie jest możliwe do ustalenia, gdyż w mechanice kwantowej pojęcie toru cząstki traci sens. W modelu kwantowym mówi się jedynie o prawdopodobieństwie znalezienia elektronu w danym obszarze, a elektronowi przypisuje się pewną funkcję falową.

18. Promieniotwórczość

Promieniotwórczość

Trwałość jądra atomu jest uwarunkowana odpowiednim stosunkiem liczby neutronów do liczby protonów. Niestabilność jąder niektórych pierwiastków wynika ze zbyt dużej lub zbyt małej liczby neutronów w jądrze.

Każda reakcja jądrowa jest związana z efektem energetycznym. Wynika on z defektu masy.

gdzie:
E - wartość efektu energetycznego,
m - masa,
c - prędkość światła w próżni (ok. 300000 km • s^-1)

Promieniotwórczość może być naturalna lub sztuczna. Najczęściej spotykanymi przemianami jądrowymi są rozpady promieniotwórcze.

Promieniowanie α to rodzaj promieniowania jonizującego cechującego się małą przenikalnością. Promieniowanie alfa jest to strumień jąder helu.

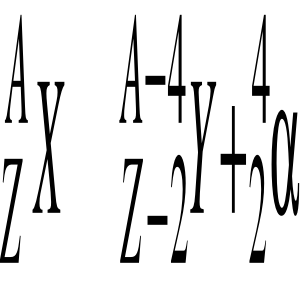
Jeżeli jądro atomu wyrzuci cząstkę

to liczba atomowa tego pierwiastka maleje o dwa, a liczba masowa o cztery, np.

Przemiana β^- polega na przemianie neutronu w proton (n › p + e^- + ν ) dlatego promieniowanie to ma również charakter korpuskularny i stanowi strumień pędzących elektronów. Jeżeli jądro atomu wyrzuci cząstkę:

to atom nie zmienia swojej liczby masowej, zwiększa się tylko o jeden jego liczba atomowa, np.

Przemiana β⁺- polega na przemianie protonu w neutron (p › n + e⁺ + ν) i dlatego promieniowanie to stanowi strumień pozytonów. Liczba masowa atomu nie zmienia się, a liczba atomowa zmniejsza się o jeden, np.

Promieniowanie γ towarzyszące przemianom α i ß, jak również rozszczepieniu jąder, jest promieniowaniem elektromagnetycznym. Emisji tego promieniowania nie towarzyszy zmiana liczby masowej lub atomowej nuklidów.

Właściwości promieniowania α:

-ma wielką przenikliwość jest bardzo dobrze pochłaniane przez większość substancji
-powoduje reakcję rozpadu, silnie zaczernia kliszę fotograficzną
-ma dużą zdolność jonizującą

Właściwości promieniowania β:

-bardzo dobrze oddziaływujące z polami magnetycznymi i elektrycznymi
-jest bardziej przenikliwe niż α;
-ma mniejszą zdolność jonizującą
-ma mniejszą szkodliwość biologiczną ale jest bardziej skuteczne od promieniowania α

Właściwości promieniowania γ:

-promieniowanie bardzo przenikliwe
-jonizuje ośrodek ale zdolność jonizująca jest niewielka
-szkodliwość promieniowania jest niewielka, natomiast skuteczność wysoka

11

---