 | Pobierz cały dokument analiza.sygnalow.i.identyfikacja.procesow.agh.doc Rozmiar 568 KB |
Analiza Sygnałów i Identyfikacja Procesów
Zadanie nr 90
Zadany układ:
gdzie: R1=600Ω
R2=1000 Ω
tp=0.0001s
Identyfikacja obiektu G1 na podstawie odpowiedzi skokowej układu.
Badany układ jest obwodem RLC wiec jego transmitancja będzie miała postać:
![]()
Do obliczeń wykorzystamy jednak trochę inna postać, mianowicie:
![]()
Rys.1 Odpowiedź skokowa układu
Z wykresu odczytujemy:
y1=0.79989 y2=0.6405 Tosc=0.009s
Wzory użyte do obliczenia poszczególnych parametrów :
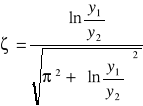
ω=2π/ Tosc 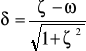
![]()
![]()
Po wyliczeniu otrzymujemy:
![]()
ω =698.13 ![]()
![]()
![]()
Transmitancja przyjmuje postać:
![]()
Wyliczone parametry układu:
![]()
![]()
Rys.2 Porównanie odpowiedzi układu zadanego i zidentyfikowanego
Identyfikacja obiektu G1 na podstawie char. amplitudowo-częstotliwościowej
Po zróżniczkowaniu odpowiedzi skokowej układu otrzymujemy odp. impulsową:
Rys.3 Charakterystyka impulsowa zadanego ukladu
Po poddaniu odpowiedzi impulsowej transformacji Fouriera otrzymujemy wykres:
Rys.4 Charakterystyka amplitudowo-częstotliwościowa zadanego ukladu układu
Wyznaczamy częstotliwości dla których cześć urojona równa się rzeczywistej oraz dla których cześć rzeczywista się zeruje(wykres przecina się z osią urojoną)
Otrzymujemy:
![]()
![]()
Z poniższych wzorów wyliczamy:
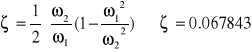
![]()
Cała transmitancja ma postać: ![]()
![]()
![]()
Rys.5 Porównanie odpowiedzi układu zadanego i zidentyfikowanego w pkt. 2
Identyfikacja parametrów modelu obiektu SISO
Po poddaniu wejścia i wyjścia układu transformacji Fouriera oraz korzystając z własności funkcji widmowej mocy wzajemnej i własnej otrzymujemy:
![]()
Charakterystyka częstotliwościowa prezentuje się następująco:
Rys.6 Charakterystyka amplitudowo-częstotliwościowa układu (po uwzględnieniu wejścia i wyjścia)
Podobnie jak w punkcie 2 wyznaczamy częstotliwości
![]()
![]()
Dalej otrzymujemy:
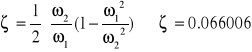
![]()
Cała transmitancja ma postać: ![]()
![]()
![]()
Rys.7 Porównanie odpowiedzi układu zadanego i zidentyfikowanego w pkt. 3
Komentarz:
 | Pobierz cały dokument analiza.sygnalow.i.identyfikacja.procesow.agh.doc rozmiar 568 KB |