Politechnika Rzeszowska

TEMAT ĆWICZENIA

Wyznaczanie rozkładu prędkości w tunelu aerodynamicznym.

CEL ĆWICZENIA

Celem ćwiczenia jest:

1. zapoznanie się z zasadą działania oraz budową:

• tunelu aerodynamicznego,

• rurki Prandtla,

• manometrów cieczowych,

określenie rozkładu prędkości przepływu w tunelu aerodynamicznym

1.Wstęp teoretyczny.

Tunele należą do grupy maszyn przepływowych, służących do sprężania i przetłaczania gazów. Ze względu na rozwiązania konstrukcyjne tunele dzieli się na otwarte i zamknięte. Wydajność tuneli zamkniętych jest znacznie większa od wydajności tuneli otwartych. Tunel składa się z wirnika łopatkowego, osadzonego na wale napędzanego silnikiem. Czynnik gazowy zasysany jest przez otwór, skąd dostaje się do przestrzeni siatek wyrównujących. Następnie gaz tłoczony jest do komory pomiarowej, w której ustawia i bada się modele lub ściąga się ciśnienie.

2.Schemat stanowiska pomiarowego:

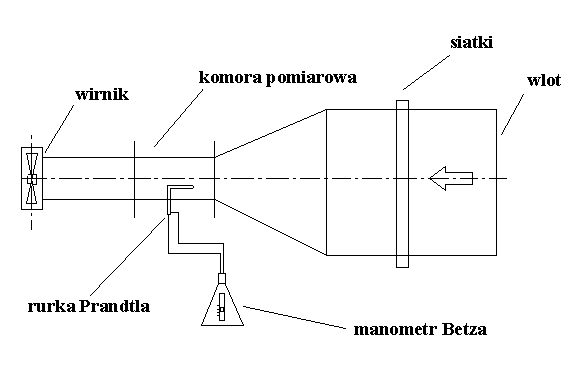
Schemat rurki Prandtla:

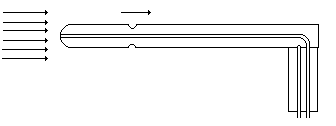
3.Przebieg ćwiczenia

Ćwiczenie polega na mierzeniu ciśnienia całkowitego za pomocą manometru Betza, który był podłączony do rurki Prandtla umieszczonej w tunelu o średnicy d=0,5 [m]. Mając ciśnienie dynamiczne obliczamy prędkość, dla danej odległości rurki Prandtla od ścianki tunelu. Pomiarów dokonywaliśmy do osi symetrii tunelu Pomiary są wykonywane w następujący sposób:

Pomiar 1 w odległości 1,5 cm od ścianki tunelu, następne pomiary 3*0,5cm; 3*1cm; 10*2cm.

4.Tabela pomiarów.

Lp.	Odległość rurki od ścianki hr	Wskazania manometru hm
		[cm]	[mm]
1	1,5	75,5
2	2,0	76,0
3	2,5	76,2
4	3,0	76,4
5	4,0	76,0
6	5,0	76,1
7	6,0	75,5
8	8,0	74,8
9	10,0	74,2
10	12,0	73,4
11	14,0	73,6
12	16,0	73,2
13	18,0	73,2
14	20,0	73,4
15	22,0	73,6
16	24,0	73,6
17	26,0	73,4

5.Obliczanie wielkości potrzebnych do wyznaczania charakterystyki.

Zamiana jednostek:

1 [mmH₂O] = 9,8 [Pa].

R_e=V_śrd_tun/υ ; gdzie R_e - liczba Reynoldsa,

υ - kinematyczny współczynnik lepkości;

υ = μ/ρ , μ - lepkość dynamiczna;

μ = 170,8 *10^-7[ N/m² ] ;

ρ = 1,21[kg/m³] ;

υ = 1,41 *10^-5[m²/s]

d - średnica przestrzeni pomiarowej; d = 0,5 [m]

Q = 2ΠrVz ; r = 25 [cm] ;

Q = 4,41[m^3/s]

5a. Obliczenia:

ρ _wody = 1000 kg/m³

ρ _powietrza = 1,2 kg/m³

g = 9,81 m/s²

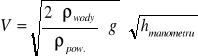
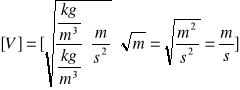
5b.Obliczenia prędkości:

5c.Obliczenia prędkości średniej:

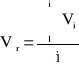
5d. Wydatek:

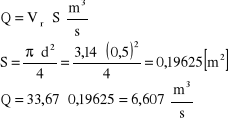
5e.Stosunek prędkości:

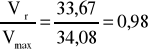
5f. Liczba Reynoldsa

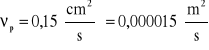
5g.Ciśnienie dynamiczne:

6.Błąd pomiaru:

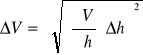
Dla Betza -

7.Tabela obliczeń.

Lp.	hr	hm	V	pd
		[m]	[mm H2O]	[m/s]	[Pa]
1	0,015	75,5	33,88	7,69
2	0,02	76,0	33,99	7,74
3	0,025	76,2	34,04	7,76
4	0,03	76,4	34,08	7,78
5	0,04	76,0	33,99	7,74
6	0,05	76,1	34,02	7,75
7	0,06	75,5	33,88	7,69
8	0,08	74,8	33,72	7,62
9	0,10	74,2	33,59	7,56
10	0,12	73,4	33,41	7,48
11	0,14	73,6	33,45	7,50
12	0,16	73,2	33,36	7,46
13	0,18	73,2	33,36	7,46
14	0,20	73,4	33,41	7,48
15	0,22	73,6	33,45	7,50
16	0,24	73,6	33,45	7,50
17	0,26	73,4	33,41	7,48

8. Wykres (znajduje się na następnej stronie).

9.Wnioski.

Otrzymane wykresy na podstawie obliczeń,.mają podobny charakter do wykresów teoretycznych zawartych w literaturze. Nieznaczne odchylenia spowodowane są błędami pomiarowymi związanymi z niedokładnością odczytu. oraz z niestarannością przeprowadzania ćwiczenia. Dokonaliśmy pomiarów w tunelu ciśnienia w różnej odległości od ścianki i okazuje się że, przy liczbie R_e=7,44*10^-8 wydatek wynosi Q =0,01 [m³/s],a prędkość V =0,021 [m/s].

1

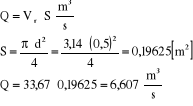
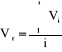
ciśnienie statyczne

p_s

p_∞

V_∞

ciśnienie całkowite

p₀

V₁≈V_∞

---