STEROWANIE KOMPUTEROWE
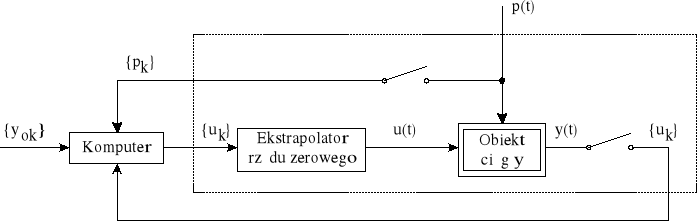
Wymagania:
relacje między
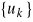
,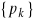
,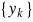
;możliwość wyboru kroku próbkowania;
znajomość równań rekurencyjnych algebraicznych sterowania (odpowiedniki regulatorów analogowych).
REGULACJA KASKADOWA
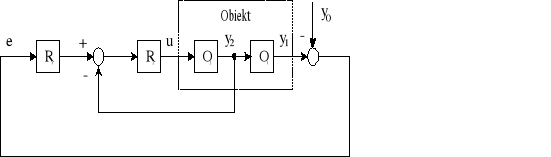
Regulator ![]()
zmniejsza czas regulacji sygnału ![]()
i linearyzuje część ![]()
obiektu.
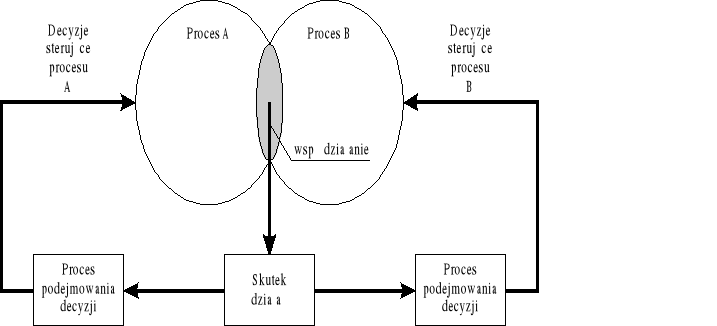
UKŁADY ROZGRYWAJĄCE
Układy rozgrywające powiązane są ściśle z teorią gier oraz procesami gospodarczymi.
Ocena jakości takich procesów dokonywana jest na podstawie indywidualnych własnych kryteriów.
Działanie układu łatwo prowadzi do konfliktu spowodowanego odmiennymi lub wręcz sprzecznymi kryteriami dla procesu A i B. Każda ze stron maksymalizuje własne kryteria jakości. Znane są tylko własne działania i ich globalne skutki.
TYPOWE WYMUSZENIA
Lp. |
Nazwa wymuszenia |
Wykres wymuszenia |
Równanie |
|
|
|
|
|
|
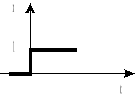
1 |
skok jednostkowy (funkcja Heaviside'a) |
|
|
|
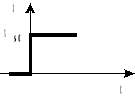
2 |
wymuszenie skokowe o dowolnej wartości |
|
|
|
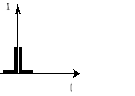
3 |
wymuszenie impulsowe (funkcja Diraca) |
|
|
|
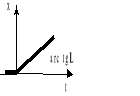
4 |
wymuszenie liniowo narastające (skok prędkości) |
|
|
|
5 |
wymuszenie paraboliczne (skok przyspieszenia) |
|
|
|
SCHEMATY BLOKOWE
Zasady przekształcania schematów blokowych w celu ich uproszczenia i określenia transmitancji układu nazywane są algebrą schematów blokowych. W tablicy podano zestawienie zasadniczych przykładów takich przekształceń, których znajomość wystarcza do określenia transmitancji dowolnie złożonego układu.
W przypadku braku w torze głównym połączeń równoległych oraz istnienia dużej ilości połączeń szeregowych i sprzężeń zwrotnych, wygodnie jest skorzystać z metody mnemonicznej, pozwalającej określić transmitancję układu bez dokonywania żadnych przekształceń schematu.
Przy korzystaniu z metody mnemonicznej postępujemy następująco:
Ustalamy, ilość torów, którymi można przejść od wyjścia do wejścia układu tak, aby kierunek poruszania się w częściach gałęzi głównej był przeciwny do kierunku przekazywania sygnału, zaś w częściach gałęzi sprzężeń zwrotnych zgodny z kierunkiem przekazywania sygnału.
Dla każdego toru tworzymy ułamki, których licznikiem jest iloczyn transmitancji członów gałęzi sprzężeń zwrotnych występujących w danym torze, a mianownikiem iloczyn transmitancji występujących w nim członów gałęzi głównej.
Odwrotność transmitancji układu jest sumą ułamków utworzonych w punkcie 2, przy czym, przy sprzężeniu zwrotnym dodatnim ułamek otrzymuje znak "-" zaś przy ujemnym znak "+".
Lp. |
Nazwa połączenia |
Schemat pierwotny |
Schemat zastępczy |
1 |
Połączenie szeregowe |
|
|
2 |
Połączenie równoległe |
|
|
3 |
Sprzężenie zwrotne |
|
|
4 |
Zmiana kolejności bloków |
|
|
5 |
Zmiana kolejności węzłów sumacyjnych |
|
|
6 |
Zmiana kolejności węzłów informacyjnych |
|
|
7 |
Przesunięcie węzła sumacyjnego przed blok |
|
|
8 |
Przesunięcie węzła informacyjnego przed węzeł sumacyjny |
|
|
9 |
Przeniesienie węzła sumacyjnego za blok |
|
|
10 |
Przeniesienie węzła informacyjnego przed blok |
|
|
11 |
Przeniesienie węzła informacyjnego za blok |
|
|
12 |
Przeniesienie węzła informacyjnego za węzeł sumacyjny |
|
|
CHARAKTERYSTYKI CZASOWE
Charakterystyką (odpowiedzią) impulsową g(t) układu liniowego stacjonarnego nazywamy odpowiedź tego układu na wymuszenie w postaci funkcji Diraca ![]()
przy zerowych warunkach początkowych. Charakterystyka impulsowa jest oryginałem transmitancji operatorowej G (s) tego układu.
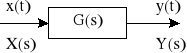
![]()
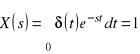
![]()
![]()
- odpowiedź impulsowa
![]()
Charakterystyką (odpowiedzią) skokową (jednostkową) h(t) układu liniowego stacjonarnego nazywamy odpowiedź tego układu na wymuszenie w postaci jednostkowej funkcji skokowej ![]()
przy zerowych warunkach początkowych. Charakterystykę skokową można określić doświadczalnie, rejestrując odpowiedź układu wywołaną wymuszeniem o stałej wartości, równej jedności, przy zerowych warunkach początkowych.
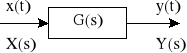
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Charakterystyka impulsowa g(t) jest równa pochodnej względem czasu charakterystyki skokowej h(t) tego układu, gdy ![]()
.
TRANSMITANCJA WIDMOWA
Transmitancją widmową ![]()
układu liniowego stacjonarnego nazywamy wielkość określaną jako stosunek wartości zespolonej składowej wymuszonej odpowiedzi ![]()
, wywołanej wymuszeniem sinusoidalnym, do wartości zespolonej tego wymuszenia ![]()
.
![]()
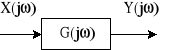
Schemat blokowy jednowymiarowego układu liniowego stacjonarnego
Transmitancja widmowa jest wielkością zespoloną, zależną od parametrów układu i pulsacji wymuszenia ![]()
![]()
przy czym
![]()
Część rzeczywista ![]()
transmitancji widmowej ![]()
jest funkcją parzystą, a część urojona ![]()
— funkcją nieparzystą pulsacji ![]()
, czyli:
![]()
Transmitancja widmowa ![]()
jest związana z transmitancją operatorową G(s) układu liniowego zależnością:
![]()
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE
Charakterystykami częstotliwościowymi nazywamy różne postacie wykresów (zależności) transmitancji widmowej w funkcji pulsacji ![]()
. Do najczęściej spotykanych charakterystyk częstotliwościowych należą:
charakterystyka amplitudowo-fazowa,
charakterystyka amplitudowa i charakterystyka fazowa,
charakterystyka logarytmiczna amplitudowa i charakterystyka logarytmiczna fazowa,
charakterystyka logarytmiczna amplitudowo-fazowa.
Charakterystyką amplitudowo-fazowa nazywamy wykres transmitancji widmowej ![]()
na płaszczyźnie zmiennej zespolonej, przy czym na osi rzeczywistej odkładamy część rzeczywistą ![]()
a na osi urojonej - część urojoną ![]()
transmitancji widmowej ![]()
.
Charakterystyka amplitudowo-fazowa
Każdemu punktowi krzywej ![]()
jest przyporządkowana odpowiednia wartość
pulsacji ![]()
. Wektor łączący początek układu współrzędnych z punktem krzywej odpowiadającym rozpatrywanej pulsacji (np. ![]()
) przedstawia transmitancję widmową dla tej pulsacji, ![]()
. Moduł tego wektora jest równy modułowi transmitancji widmowej ![]()
, a kąt ![]()
zawarty między dodatnim zwrotem osi liczb rzeczywistych i tym wektorem jest równy argumentowi transmitancji widmowej dla tej pulsacji.
Charakterystyki amplitudowo-fazowe rzeczywistych (realizowalnych) układów dynamicznych dążą do początku układu współrzędnych, gdyż ![]()
dla ![]()
.
Charakterystyką amplitudową (modułu) nazywamy wykres (zależność) modułu transmitancji widmowej ![]()
w funkcji pulsacji ![]()
(rys. a), a charakterystyką fazową — wykres (zależność) argumentu (fazy) transmitancji widmowej ![]()
w funkcji pulsacji ![]()
(rys. b). Charakterystyka amplitudowa i charakterystyka fazowa łącznie dają tę samą informację o układzie, co jedna charakterystyka amplitudowo-fazowa.
Charakterystyki logarytmiczne: a) logarytmiczna charakterystyka amplitudowa;
b) logarytmiczna charakterystyka fazowa
Logarytmiczną charakterystyką amplitudową (modułu) nazywamy wykres ![]()
w funkcji ![]()
(rys. a), a logarytmiczną charakterystyką fazową - wykres ![]()
? w funkcji ![]()
(rys. b). Wykreślając logarytmiczną charakterystykę amplitudową, na osi odciętych odkładamy logarytm dziesiętny pulsacji ![]()
(logarytmiczna skala pulsacji), a na osi rzędnych 20 logarytmów dziesiętnych modułu transmitancji widmowej (w decybelach) czyli tzw. moduł logarytmiczny oznaczany ![]()
lub w skrócie ![]()
. W przypadku logarytmicznej charakterystyki fazowej na osi odciętych odkładamy logarytm dziesiętny pulsacji ![]()
, a na osi rzędnych kąt ![]()
(w stopniach lub radianach). Dziesięciokrotną zmianę pulsacji nazywamy dekadą, a dwukrotną — oktawą. Logarytmiczną charakterystykę amplitudową można aproksymować charakterystyką asymptotyczną mającą postać łamanej złożonej z prostych odcinków o nachyleniach będących całkowitą wielokrotnością 20 dB/dekadę.
Zasadniczym powodem stosowania charakterystyk logarytmicznych jest łatwość wyznaczania charakterystyk asymptotycznych prostych członów i charakterystyk wypadkowych układów złożonych z kilku prostych członów.
Charakterystyki logarytmiczne: a) logarytmiczna charakterystyka amplitudowa;
b) logarytmiczna charakterystyka fazowa
Logarytmiczną charakterystyką amplitudowo-fazową nazywamy wykres (zależność) ![]()
w funkcji ![]()
. Wykreślając logarytmiczną charakterystykę amplitudowo-fazową, na osi odciętych odkładamy argument transmitancji widmowej ![]()
(w stopniach lub radianach), a na osi rzędnych 20 logarytmów dziesiętnych modułu tej transmitancji widmowej (w decybelach).
Charakterystyka logarytmiczna amplitudowo-fazowa
Logarytmiczna charakterystyka amplitudowo-fazową łączy w sobie zalety charakterystyk logarytmicznych i charakterystyki amplitudowo-fazowej.
|
70 |
|
Wykład |
Wyszukiwarka
Podobne podstrony:
kon0, automatyka konspekt
kon6, automatyka konspekt
regulatory, automatyka konspekt
kon13, automatyka konspekt
stabilność, automatyka konspekt
Konspekt wykładów z Podstaw automatyki wykład 5
Konspekt korektywa FIN (Automatycznie zapisany) 2
konspekt automatyka
konspekt wydruk (Automatycznie zapisany)
Elemety log-konspekt, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty,
Konspekt wykładów z Podstaw automatyki wykład 5
Ekonomia konspekt1
FESTO Podstawy automatyzacji
Automatyka (wyk 3i4) Przel zawory reg
Automatyzacja w KiC (w 2) Obiekty reg
BLS 2010 stom [konspekt]ppt
więcej podobnych podstron