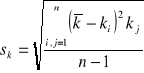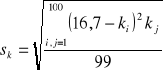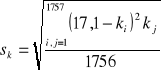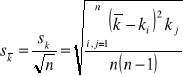Cel ćwiczenia: Sprawozdanie ocenione na 5 (Wosińska)
Celem ćwiczenia jest prześledzenie procesu powstawania błędów przypadkowych przy użyciu tablicy Galtona. Celem doświadczenia jest także porównanie otrzymanego rozkładu wyników z rozkładem teoretycznym Gaussa. W ćwiczeniu należy także określić warunki, w jakich tablicę Galtona można wykorzystywać do symulacji procesu powstawania błędów przypadkowych.
Wykonanie ćwiczenia:
Ćwiczenie przeprowadziliśmy przy pomocy tablicy Galtona. Przyrząd ten składa się z wielu rzędów kołeczków umieszczonych na płaskiej tablicy ustawionej pionowo lub pod pewnym kątem do pionu. Na kołeczki spuszcza się z góry kulki, które tocząc się po tablicy w dół zderzają się z kołeczkami i wpadają do przegródek umieszczonych w dolnej części tablicy. W wyniku wielokrotnych zderzeń kulki przemieszczają się także w kierunku poziomym. Ruch kulki na tablicy Galtona stanowi model procesu powstawania błędu przypadkowego. Wynikowi pomiaru odpowiada numer przegródki, do której trafiła kulka, zaś całkowite poziome przemieszczenie kulki błędowi przypadkowemu jaki towarzyszy pomiarowi. Zrealizowaliśmy szereg niezależnych serii pomiarowych składających się z różnej liczby elementów (kulek). Maksymalna ilość elementów była określona parametrami tablicy - wysokość kolumny.
Wyniki pomiarów przedstawiono w tabelach 1- 5:
Dla 20 pomiarów:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
4 |
2 |
1 |
1 |
1 |
2 |
1 |
|
1 |
|
|
1 |
|
|
|
1 |
|
Tabela 1
Dla 50 pomiarów:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
|
|
|
|
|
|
|
2 |
|
|
1 |
4 |
2 |
2 |
3 |
3 |
5 |
5 |
4 |
2 |
4 |
1 |
3 |
4 |
2 |
1 |
1 |
1 |
|
|
|
|
Tabela 2
Dla 100 pomiarów:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
|
|
|
|
1 |
1 |
|
2 |
4 |
1 |
1 |
3 |
6 |
4 |
5 |
6 |
12 |
11 |
7 |
10 |
7 |
5 |
6 |
3 |
1 |
1 |
|
|
1 |
|
2 |
|
Tabela 3
Dla 687 pomiarów:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
|
2 |
1 |
3 |
6 |
3 |
5 |
10 |
9 |
7 |
18 |
18 |
31 |
40 |
33 |
54 |
54 |
53 |
51 |
53 |
50 |
38 |
43 |
24 |
13 |
42 |
5 |
5 |
7 |
2 |
3 |
4 |
Tabela 4
Dla 1767 pomiarów:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
|
5 |
3 |
4 |
11 |
4 |
13 |
22 |
24 |
35 |
43 |
49 |
88 |
97 |
98 |
131 |
141 |
160 |
144 |
138 |
128 |
95 |
92 |
50 |
39 |
72 |
15 |
15 |
19 |
6 |
8 |
8 |
Tabela 5
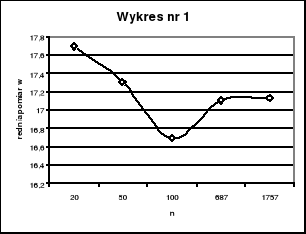
Na podstawie wyników badań obliczyliśmy wartości średnie pomiarów dla liczby pomiarów n = 20, 50, 100, 687, 1767. Zależność ![]()
przedstawia wykres nr 1
|
|
Dla 20
Dla 50
Dla 100
Dla 687
Dla 1757 |
n 20 50 100 687 1757
17,70 17,30 16,69 17,11 17,13
|
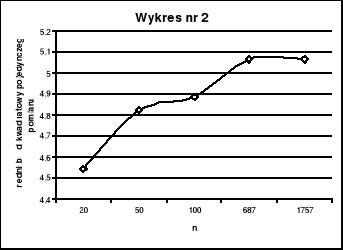
Analogicznie obliczyliśmy wartości średniego błędu kwadratowego pojedynczego pomiaru (wykres nr 2)
|
|
Dla 20
Dla 50
Dla 100
Dla 687
Dla 1757 |
n 20 50 100 687 1757
4,54 4,82 4,89 5,07 5,07
|
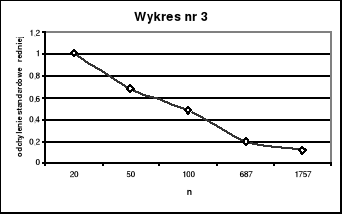
oraz odchylenie standardowe średniej (wykres nr 3)
|
|
Dla 20
Dla 50
Dla 100
Dla 687
Dla 1757 |
n 20 50 100 687 1757
1,02 0,68 0,49 0,20 0,12
|
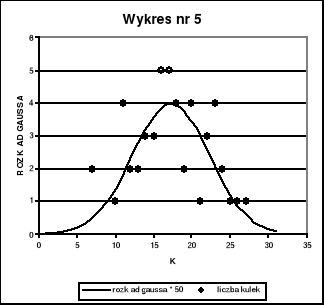
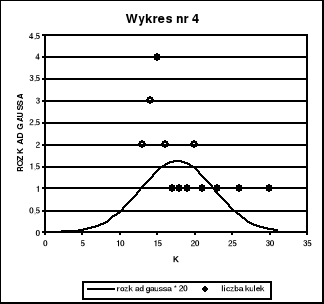
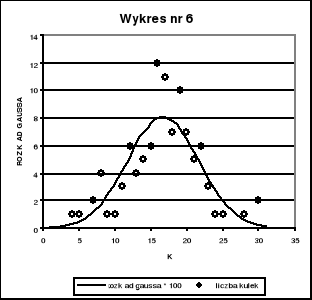
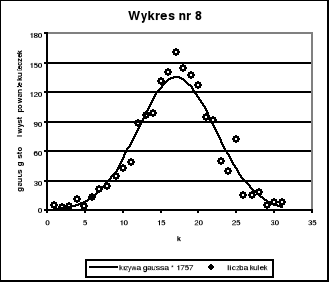
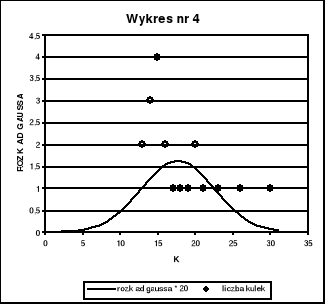
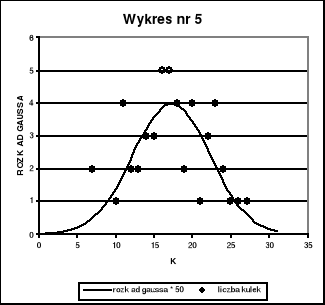
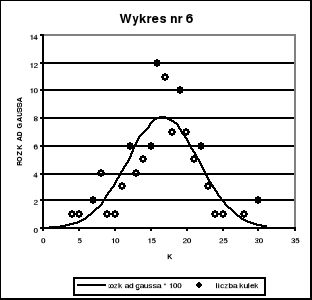
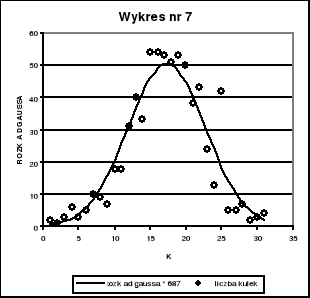
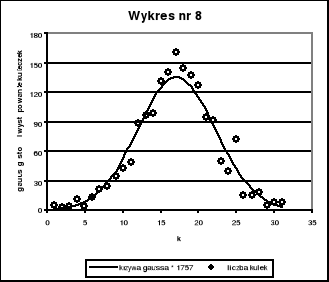
Na wykresie nr 4, 5, 6, 7, 8 przedstawiliśmy jednocześnie (w celu lepszej prezentacji wniosków) histogram wyników pomiarów dla poszczególnych n = 20, 50, 100, 687, 1757 oraz funkcję rozkładu Gaussa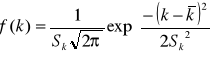
pomnożoną przez n (liczbę pomiarów).

Następnie policzyliśmy wartość testu ![]()
dla liczby pomiarów n = 1757. Test ten służy do weryfikacji zgodności rozkładu normalnego z rozkładem wyników uzyskanych w doświadczeniu przeprowadzonym dla n kulek.
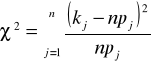
, gdzie ![]()
- prawdopodobieństwo uzyskania wielkości ![]()
(f-cja Gaussa)
![]()
- liczba elementów przypadających na k-ty przedział
![]()
- liczba wszystkich pomiarów
Dodatkowo wprowadziliśmy wielkość zwaną liczbą stopni swobody.
L = m - r -1
gdzie r jest liczbą parametrów określających rozkład teoretyczny (r = 2 dla rozkładu Gaussa), a m = 31 (rząd), toteż wykonując proste działania wyznaczamy liczbę stopni swobody na
L = 28.
Wnioski:
1. W ćwiczeniu badaliśmy zmienność parametrów: odchylenia standardowego pojedynczego pomiaru (![]()
) i odchylenia standardowego średniej (![]()
) w zależności od ilości pomiarów. Stwierdziliśmy, że ![]()
maleje wraz ze wzrostem ilości pomiarów, natomiast ![]()
nie zależy od ilości pomiarów.
2. W ćwiczeniu badaliśmy także zgodność rozkładu wyników doświadczalnych z teoretycznym rozkładem Gaussa i doszliśmy do następujących wniosków:
Na podstawie przedstawionych powyżej wyników otrzymano wartość ![]()
= 101,14. Dla 28 stopni swobody wartość ![]()
wynosi 48,3 , a więc ![]()
co oznacza, że dla poziomu ufności P = 0,01 hipoteza mówiąca, że nasze dane doświadczalne opisane są rozkładem gaussa jest fałszywa.
Dla ![]()
= 101,14 przy 28 stopniach swobody poziom ufności jest praktycznie równy 0 w stosunku poziomu ufności 0,01.
Poziom ufności P odczytaliśmy z tabeli rozkładu ![]()
umieszczonej w skrypcie CLF rachunku błędów (Tabela nr 3), dla stopnia swobody L = 28 oraz odpowiadających im wartości ![]()
przez nas obliczonych.
Obliczenia parametrów charakteryzyjących rozkład Gaussa dokonaliśmy przy pomocy programu Microsoft Excel© oraz MathCad™.
Do sprawozdania dołączamy tabelę, obliczeń potrzebnych wielkości, wykonaną w programie Microsoft Excel©.
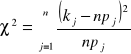
Wyszukiwarka
Podobne podstrony:
317
316 317
od str. 317-320, Negatywny wpływ telewizji na zdolności poznawcze:
Psychologia str 306-317
NEUROLOGIA I PSYCHIATRIA id 317 Nieznany
MPLP 316;317 23.06;05.07.2011
283-317, materiały ŚUM, IV rok, Patomorfologia, egzamin, opracowanie 700 pytan na ustny
317 , KURS PEDAGOGICZNY - OPOLE
biuletyn mrr nr 17 317 id 89427 Nieznany (2)
04.Badanie źródła prądowego na stabilizatorze LM 317
ZLUDZENIA, KTO RE POZWALAJA Z YC s 289 317
317 - Kod ramki - szablon, RAMKI NA CHOMIKA, Kody Gotowych Ramek
317 XUORDGJB37B2HZARCEDOI7BBJGFOLRHVOSRVGXQ
316 317 id 35103 Nieznany
317
317
317, Uczelnia, Administracja publiczna, Jan Boć 'Administracja publiczna'
więcej podobnych podstron