Sprawozdanie z laboratorium z fizyki i biofizyki

Ćwiczenie nr 4

Temat ćwiczenia: Badanie sił tarcia.

Sekcja nr 7 w składzie:

1. Anna Michałowska

2. Joanna Talik

3. Krasińska Joanna (Chem I)

Data oddania sprawozdania:………….

Ocena:….

1. Wstęp teoretyczny

Tarcie to siła, która przeciwstawia się ruchowi obiektów. Siła ta jest zawsze skierowana przeciwnie do wektora prędkości.

Siła tarcia jest niezachowawcza, co oznacza, że praca wykonana przez nią lub przeciwko niej, pomiędzy dwoma ustalonymi punktami, zależy od drogi, jaką obierzemy.

Zjawisku tarcia towarzyszy wydzielanie się ciepła, elektryzowanie się ciał, ich zniszczenie.

Źródłem tarcia są punktowe oddziaływania atomowe. Prawdopodobnie powstają wiązania pomiędzy atomami (na zasadzie oddziaływań elektrostatycznych) , należących do wypukłości obydwu oddziaływujących ze sobą powierzchni.

Wyróżniamy kilka rodzajów tarcia:

Tarcie zewnętrzne (suche)-oddziaływanie zachodzące między powierzchniami dwóch stykających się ciał stałych, które przeciwdziała ich przemieszczaniu się względem siebie. Najbardziej typowe z nich to:

• Tarcie statyczne- jeżeli ciała nie poruszają się względem siebie

• Tarcie kinetyczne- jeżeli ciała znajdują się w ruchu względem siebie

• Tarcie toczne - gdy jedno ciało toczy się po powierzchni drugiego

Tarcie wewnętrzne( lepkość)- mechanizm oporów, które występują podczas ruchu ciał w cieczach i w gazach, spowodowane przez lepkość oraz różnice ciśnień, jakie wywiera płyn na przednią i tylną ściankę poruszającego się ciała. Jeżeli ciało porusza się w ośrodku płynnym to cienka warstwa płynu przylega do niego i tarcie odbywa się pomiędzy warstewkami tego płynu(cieczy lub gazu).

Maksymalna siła tarcia działająca między dowolną parą suchych (nie pokrytych żadnym smarem) powierzchni podlega dwóm prawom empirycznym:

• Maksymalna siła tarcia jest w przybliżeniu niezależna od wielkości powierzchni zetknięcia w bardzo szerokim zakresie;

• Maksymalna siła tarcia jest proporcjonalna do siły normalnej (F_N), tzn. siły jaką jedna powierzchnia naciska na drugą.

Współczynnik tarcia statycznego jest to stosunek maksymalnej wartości siły tarcia statycznego F_S do wartości siły normalnej i oznaczamy go μ_s:

Dla tarcia kinetycznego:

gdzie: μ_k -współczynnik tarcia kinetycznego

Maksymalna siła tarcia statycznego jest równa najmniejszej sile, jaką należy przyłożyć do ciała, aby je ruszyć z miejsca.

Najczęściej μ_s > μ_k , ponieważ wprawienie ciała w ruch wymaga przyłożenia większej siły niż utrzymanie tego samego ciała w ruchu.

2. Przebieg ćwiczenia

Część 1a)

Pomiar współczynnika tarcia za pomocą równi pochyłej.

Wykonywane czynności:

Kładziemy badany klocek na równi pochyłej, po czym powoli nachylamy powierzchnię równi do momentu, w którym badany klocek zaczyna się zsuwać. W tym momencie odczytujemy wartość kąta nachylenia równi. Następnie dobieramy takie nachylenie równi, aby klocek poruszał się ruchem jednostajnym. Gdy tak się stanie, odczytujemy wartość kąta nachylenia równi. Pomiary powtarzamy sześciokrotnie dla każdego rodzaju klocka.

Tabele wyników:

Nr	Materiał powierzchni równi	Materiał powierzchni klocka	αs[˚]	αk[˚]	µs=tg αs	µk=tg αk
1.1	drewno	drewno	31	18	0,60	0,32
1.2					36	23	0,73	0,42
1.3					37	25	0,75	0,47
1.4					38	25	0,78	0,47
1.5					35	24	0,70	0,44
1.6					36	22	0,73	0,40
Wartość średnia					0,71		0,42
Odchylenie standardowe					0,06		0,05

Wynik końcowy:

Dla drewna

Nr	Materiał powierzchni równi	Materiał powierzchni klocka	αs[˚]	αk[˚]	µs=tg αs	µk=tg αk
2.1	drewno	metal	26	15	0,49	0,27
2.2					24	17	0,44	0,31
2.3					25	18	0,47	0,32
2.4					24	18	0,44	0,32
2.5					25	19	0,47	0,34
2.6					24	18	0,44	0,32
Wartość średnia					0,46	0,31
Odchylenie standardowe					0,02	0,02

Dla metalu

Nr	Materiał powierzchni równi	Materiał powierzchni klocka	αs[˚]	αk[˚]	µs=tg αs	µk=tg αk
3.1	drewno	guma	33	22	0,65	0,40
3.2					33	22	0,65	0,40
3.3					35	21	0,70	0,38
3.4					34	23	0,67	0,42
3.5					35	22	0,70	0,40
3.6					33	24	0,65	0,44
Wartość średnia					0,67	0,41
Odchylenie standardowe					0,02	0,02

Dla gumy

Część 1b)

Pomiar współczynnika tarcia kinetycznego.

Wykonywane czynności:

Badany klocek kładziemy na płaskiej powierzchni. Zaczepiamy o niego dynamometr i ciągniemy klocek za pomocą dynamometru do momentu, w którym będzie się on przesuwał ruchem jednostajnym. Odczytujemy na skali dynamometru wartość siły z jaką działaliśmy na klocek. Pomiary powtarzamy sześciokrotnie dla każdego rodzaju klocka.

Tabele wyników:

Nr	Materiał powierzchni równi	Materiał powierzchni klocka	Masa klocka mk	Fd[N]	µk=Fd/gmk
1.1	drewno	drewno	140g=0,14kg	0,75	0,55
1.2							0,5	0,36
1.3							0,4	0,29
1.4							0,5	0,36
1.5							0,7	0,51
1.6							0,6	0,44
Wartość średnia					0,42
Odchylenie standardowe					0,09

dla drewna:

Nr	Materiał powierzchni równi	Materiał powierzchni klocka	Masa klocka mk	Fd	µk=Fd/gmk
2.1	drewno	metal	180g=0,18kg	0,25	0,14
2.2							0,25	0,14
2.3							0,2	0,11
2.4							0,25	0,14
2.5							0,4	0,23
2.6							0,3	0,17
Wartość średnia					0,16
Odchylenie standardowe					0,04

dla metalu:

Nr	Materiał powierzchni równi	Materiał powierzchni klocka	Masa klocka mk	Fd	µk=Fd/gmk
3.1	drewno	guma	150g=0,15kg	0,5	0,34
3.2							0,7	0,48
3.3							0,4	0,27
3.4							0,4	0,27
3.5							0,6	0,41
3.6							0,6	0,41
Wartość średnia					0,36
Odchylenie standardowe					0,08

dla gumy:

Część 2

Wyznaczanie współczynnika tarcia przy toczeniu.

Wykonywane czynności:

Na równi pochyłej kładziemy badany walec. Następnie powoli nachylamy powierzchnię równi do momentu, w którym walec zaczyna się zsuwać. Wtedy odczytujemy wartość kąta nachylenia równi. Pomiary powtarzamy sześciokrotnie dla każdego rodzaju walca.

Tabele wyników:

Nr	Promień podstawy walca (r)	αg[°]	µT=r*tg αg[m]
1.1	1,6cm= 0,016 m	6	0,016*0,1=0,0016
1.2			6	0,0016
1.3			8	0,016*0,14=0,0022
1.4			7	0,016*0,12=0,0019
1.5			7	0,0019
1.6			6	0,0016
Wartość średnia			0,0018
Odchylenie standardowe			0,0002

Wynik końcowy:

Nr	Promień podstawy walca (r)	αg[°]	µT=r*tg αg[m]
2.1	1,1cm=0,011m	7	0,011*0,12=0,0013
2.2			6	0,011*0,1=0,0011
2.3			7	0,0013
2.4			6	0,0011
2.5			7	0,0013
2.6			5	0,011*0,09=0,00099~0,0001
Wartość średnia			0,001
Odchylenie standardowe			0,0004

Nr	Promień podstawy walca (r)	αg[°]	µT=r*tg αg[m]
3.1	0,8cm=0,008m	5	0,008*0,09=0,0007
3.2			6	0,008*0,1=0,0008
3.3			5	0,0007
3.4			5	0,0007
3.5			6	0,0008
3.6			5	0,0007
Wartość średnia			0,0007
Odchylenie standardowe			~0

Część 3

Wyznaczanie stosunku współczynników tarcia przy toczeniu i ślizganiu.

Wykonywane czynności:

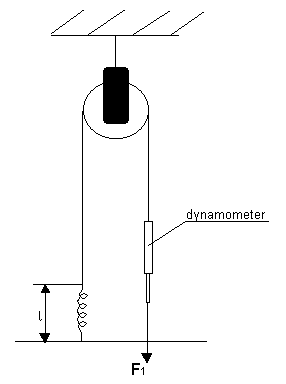
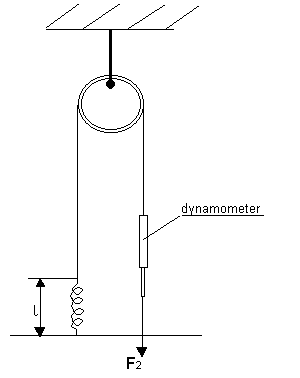
W celu wyznaczenia siły tarcia przy toczeniu i ślizganiu korzystano z poniższego układu pomiarowego:

Za pomocą dynamometru rozciągamy sprężynę do długości l i zapisujemy wartość siły jaką musimy zadziałać. Pomiar przeprowadzamy, gdy bloczek jest zablokowany oraz dla gdy nie ma blokady. Pomiary przeprowadzamy sześciokrotnie dla każdej z trzech długości sprężyny, dla zablokowanego i odblokowanego bloczka. Obliczamy stosunek F₁/F₂.

Długość sprężyny bez rozciągania = 6 cm.

Obliczamy współczynnik sprężystości sprężyny korzystając ze wzoru:

k = F/x [N/m] gdzie, x - odkształcenie sprężyny

Tabele wyników:

Rozciągnięcie sprężyny	k[N/m]		F1[N]	F2[N]	F1/F2
L1=3cm=0,03m	dla F1 śr	dla F2 śr	4,5	1,8	2,5
		133	57	4,8	1,7	2,8
						5	1,8	2,8
						3	1,7	1,8
						5,2	1,6	3,3
						1,3	1,6	0,8
Wartość średnia			4,0	1,7	2,3
Odchylenie standardowe			1,4	0,1	0,8

Rozciągnięcie sprężyny	k[N/m]		F1[N]	F2[N]	F1/F2
L2=5cm=0,05m	dla F1 śr	dla F2 śr	8,2	3,4	2,4
		154	68	7,4	3,3	2,2
						7,6	3,5	2,2
						7,9	3,4	2,3
						7,8	3,4	2,3
						7,4	3,3	2,2
Wartość średnia			7,7	3,4	2,3
Odchylenie standardowe			0,3	0,1	0,1

Rozciągnięcie sprężyny	k[N/m]		F1[N]	F2[N]	F1/F2
L4=4cm=0,04m	dla F1 śr	dla F2 śr	6,1	2,6	2,3
		150	65	6	2,5	2,4
						6	2,4	2,5
						5,8	2,6	2,2
						6	2,6	2,3
						6	2,8	2,1
Wartość średnia			6	2,6	2,3
Odchylenie standardowe			0,1	0,1	0,1

Wnioski

Przeprowadzając powyższe doświadczenia doszliśmy do następujących wniosków:

• współczynnik tarcia statycznego (jego wartość maksymalna) jest większy niż współczynnik tarcia kinetycznego;

• siła tarcie nie zależy od pola powierzchni stykających się ciał

• siła tarcia zależy od materiału z jakiego wykonane są stykające się powierzchnie;

• tarcie przy ślizganiu stawia opory około 2 razy większe niż tarcie przy toczeniu;

• współczynnik tarcia tocznego zależy od promienia walca, teoretycznie im większy promień tym mniejszy współczynnik tarcia. Niestety w naszych pomiarach nie można zaobserwować tej zależności - wraz ze wzrostem promienia wzrasta współczynnik tarcia tocznego. Błąd ten jest wynikiem niedokładności pomiarów, niedokładnego odczytania wartości kąta, a także nierówności powierzchni równi).

Zauważamy nieznaczne różnice między wartościami μ_k ( dla gumy i drewna, ponieważ w wypadku metalu rozbieżność jest znacząca) mierzonymi za pomocą równi pochyłej, a wartościami μ_k, które otrzymaliśmy wykonując pomiary za pomocą dynamometru . Przyczyną tych różnic jest prawdopodobnie błąd w odczycie kąta nachylenia równi, wartości wskazywanych przez dynamometr, oraz nierówności powierzchni równi.

---