Przemysław Ryczek gr.III Mba

DANE: N = 9 kW; n₁ = 6500 obr/min; i = 1:18; z₁ = z₃ = 17

1. Wyliczenie prędkości obrotowych na poszczególnych wałkach.

obr/min
obr/min

gdzie:

• i₁ - przełożenie pierwszej pary kół zębatych,

• n₁ - prędkość na wejściu przekładni,

- n₂ - prędkość na drugim wałku,

• i₂ - przełożenie drugiej pary kół zębatych,

• n₃ - prędkość na wyjściu z przekładni.

2. Wyznaczenie momentów obrotowych na poszczególnych wałkach.

gdzie:

• M₁, M₂, M₃ - momenty obrotowe na poszczególnych wałkach,

• n₁, n₂, n₃ - prędkości obrotowe na poszczególnych wałkach,

- N - moc urządzenia napędzającego przekładnię redukcyjną.

3. Wyznaczam ilość zębów na poszczególnych kołach zębatych .

gdzie:

• i₁ - przełożenie pierwszej pary kół zębatych,

• i₂ - przełożenie drugiej pary kół zębatych,

• z₁, z₂, z₃, z₄ - liczba zębów na poszczególnych kołach.

4. Obliczenie modułu.

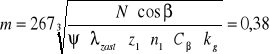
gdzie:

• m - moduł ,

• N - moc urządzenia napędzającego przekładnię redukcyjną,

• β =15 - kąt pochylenia linii zęba,

• ψ =15 - współczynnik szerokości wieńca zębatego,

• λ_zast = 3,44 - współczynnik wytrzymałości zęba dobierany na podstawie z_zast;

• z₁ - liczba zębów pierwszego koła,

• n₁ - prędkość obrotowa na pierwszym wałku,

• C_β =1,4 - współczynnik uwzględniający wpływ stopnia pokrycia,

• k_g =394,7MPa - dopuszczalne naprężenia zginające.

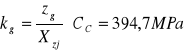
• Z_g =750 MPa- wytrzymałość zmęczeniowa na zginanie jednokierunkowe,

• X_zj = 1,9 - współczynnik bezpieczeństwa,

• C_c = 1 - współczynnik trwałości zęba.

5. Przyjęcie na podstawie PN - 78/M - 88502 modułu

Przyjmuje moduł dla pierwszej pary kół m = 2,0 mm

6. Obliczenie parametrów geometrycznych pierwszej pary kół zębatych.

		Koło I	Koło II
Szerokość wieńca zębatego:		30
Średnicy podziałowej:		35,20	140,80
Średnicy wierzchołków zębów:		39,20	144,80
Średnicy podstaw zębów:		30,80	136,40
Odległość osi:		88,00

gdzie:

• b - szerokość wieńca zębatego,

• ψ - współczynnik szerokości wieńca zębatego,

• m - moduł,

• z₁ - liczba zębów na pierwszym kole zębatym,

• z₂ - liczba zębów na drugim kole zębatym,

• β - kąt pochylenia linii zęba,

• d_p - średnica podziałowa,

• d_g - średnica wierzchołków zębów,

• d_s - średnica podstaw zębów,

- a - odległość osi pierwszego i drugiego wałka.

7. Obliczenia wytrzymałościowe.

Charakter pracy bez obciążeń prawie bez wahań, dobieram długość pracy 12 godzin.

Sprawdzam wytrzymałość zębów u podstawy

Obliczam obciążenie zastępcze ze wzoru:

N

gdzie:

• P_zast - obciążenie zastępcze,

• P_stat = 751,136 N - obciążenie statyczne,

• C_p = 1,00 - współczynnik przeciążenia,

• C_v = 1,346 - współczynnik nadwyżek dynamicznych,

= 1,346

• v - prędkość obwodowa,

• B - współczynnik zależny od wartości v,

• d_p1 - średnica podziałowa pierwszego koła,

• n₁ - prędkość obrotowa pierwszego wałka.

Obliczam obciążenie statyczne ze wzoru:

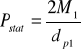
= 751,136 N

• M₁ - moment obrotowy na pierwszym wałku.

Obliczam siłę obliczeniową ze wzoru:

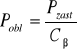
= 722,2 N

• P_obl - siła obliczeniowa,

• C_β - współczynnik uwzględniający wpływ stopnia pokrycia.

Obliczam zastępcze naprężenie zginające ze wzoru:

< k_g

MPa
MPa

• b - szerokość wieńca zębatego

• m - moduł ,

• λ_zast - współczynnik wytrzymałości zęba,

• k_g - dopuszczalne naprężenia zginające.

Sprawdzam wytrzymałość zębów z warunku na naciski powierzchniowe.

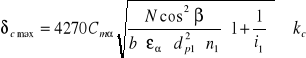
MPa
MPa

gdzie:

• δ_{c max} - naciski powierzchniowe,

• C_mα = 478,2 - współczynnik danej grupy materiałowej,

• N - moc urządzenia napędzającego przekładnię redukcyjną,

• β - kąt pochylenia linii zęba,

• ε_α - współczynnik czołowego stopnia pokrycia,

• n₁ - prędkość obrotowa pierwszego wałka,

• i₁ - przełożenie pierwszej pary kół zębatych,

• k_c - dopuszczalne naprężenia na ściskanie,

• ε_α - współczynnik czołowego stopnia pokrycia,

• C₁, C₂, C₃ - współczynniki,

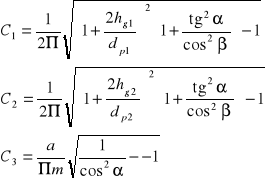
• d_p1 - średnica podziałowa pierwszego koła,

• d_p2 - średnica podziałowa drugiego koła,

• h_g1 - wysokość głowy zęba pierwszego koła,

• h_g2 - wysokość głowy zęba drugiego koła,

• m - moduł,

• a - odległość osi pierwszego i drugiego wałka,

• α = 20° - kąt przyporu,

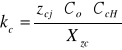
= 589 MPa

• Z_cj - wytrzymałość trwała na zmęczenie ściskaniem,

• C_o - współczynnik uwzględniający lepkość oleju,

• C_cH - współczynnik uzależniony od żądanej ilości wahnięć,

• X_zc - współczynnik bezpieczeństwa przy zmęczeniowym nacisku,

=1,188

• X_zc - współczynnik stanu powierzchni.

8. Obliczenie modułu drugiej pary kół zębatych.

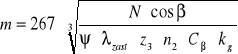
= 0,60 mm

gdzie:

• m - moduł ,

• N - moc urządzenia napędzającego przekładnię redukcyjną,

• β - kąt pochylenia linii zęba,

• ψ - współczynnik szerokości wieńca zębatego,

• λ_zast - współczynnik wytrzymałości zęba dobierany na podstawie z_zast;

• z₃ - liczba zębów pierwszego koła,

• n₂ - prędkość obrotowa na pierwszym wałku,

• C_β - współczynnik uwzględniający wpływ stopnia pokrycia,

• k_g - dopuszczalne naprężenia zginające.

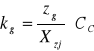
• Z_g - wytrzymałość zmęczeniowa na zginanie jednokierunkowe,

• X_zj = 1,9 - współczynnik bezpieczeństwa,

• C_c = 1 - współczynnik trwałości zęba.

9. Przyjęcie na podstawie PN - 78/M - 88502 modułu.

Przyjmuje moduł dla drugiej pary kół m=2,5 mm

10. Obliczenie parametrów geometrycznych drugiej pary kół zębatych.

	Koło III	Koło IV
Szerokość wieńca zębatego:		38
Średnicy podziałowej:		44,00	199,29
Średnicy wierzchołków zębów:		49,00	204,22
Średnicy podstaw zębów:		38,50	193,74
Odległość osi:		121,64

gdzie:

• b - szerokość wieńca zębatego,

• ψ - współczynnik szerokości wieńca zębatego,

• m - moduł,

• z₃ - liczba zębów trzeciego koła zębatego,

• z₄ - liczba zębów czwartego koła zębatego,

• β - kąt pochylenia linii zęba,

• d_p - średnica podziałowa,

• d_g - średnica wierzchołków zębów,

• d_s - średnica podstaw zębów,

• a - odległość osi drugiego i trzeciego wałka.

11. Obliczenia wytrzymałościowe.

Sprawdzam wytrzymałość zębów u podstawy.

Obliczam obciążenie zastępcze ze wzoru:

= 3055,2 N

gdzie:

• P_zast - obciążenie zastępcze,

• P_stat - obciążenie statyczne,

• C_p - współczynnik przeciążenia,

• C_v - współczynnik nadwyżek dynamicznych,

= 1,277

• v - prędkość obwodowa,

• d_p3 - średnica podziałowa trzeciego koła,

• n₂ - prędkość obrotowa drugiego wałka.

Obliczam obciążenie statyczne ze wzoru:

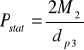
= 2392,27 N

• M₂ - moment obrotowy na drugim wałku.

Obliczam siłę obliczeniową ze wzoru:

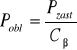
= 2182,3 N

• P_obl - siła obliczeniowa,

• C_β - współczynnik uwzględniający wpływ stopnia pokrycia.

Obliczam zastępcze naprężenie zginające ze wzoru:

MPa
MPa

• b - szerokość wieńca zębatego

• m - moduł ,

• λ_zast - współczynnik wytrzymałości zęba,

• k_g - dopuszczalne naprężenia zginające.

Sprawdzam wytrzymałość zębów z warunku na naciski powierzchniowe.

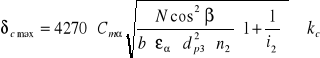
MPa
MPa

gdzie:

• δ_{c max} - naciski powierzchniowe,

• C_mα = 478,2 - współczynnik danej grupy materiałowej,

• N - moc urządzenia napędzającego przekładnię redukcyjną,

• β - kąt pochylenia linii zęba,

• ε_α - współczynnik czołowego stopnia pokrycia,

• n₂ - prędkość obrotowa drugiego wałka,

• i₂ - przełożenie drugiego pary kół zębatych,

• k_c - dopuszczalne naprężenia na ściskanie.

• ε_α - współczynnik czołowego stopnia pokrycia,

• C₁, C₂, C₃ - współczynniki,

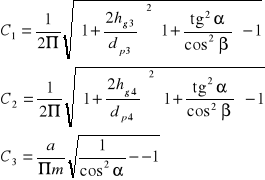
• d_p3 - średnica podziałowa pierwszego koła,

• d_p4 - średnica podziałowa drugiego koła,

• h_g3 - wysokość głowy zęba pierwszego koła,

• h_g4 - wysokość głowy zęba drugiego koła,

• m - moduł,

• a - odległość osi pierwszego i drugiego wałka,

• α = 20° - kąt przyporu,

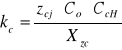
=589 MPa

• Z_cj = 600 MPa- wytrzymałość trwała na zmęczenie ściskaniem,

• C_o = 1 - współczynnik uwzględniający lepkość oleju,

• C_cH = 1 - współczynnik uzależniony od żądanej ilości wahnięć,

• X_zc = 1,188 - współczynnik bezpieczeństwa przy zmęczeniowym nacisku,

=1,188

• X_zc - współczynnik stanu powierzchni.

Oba warunki wytrzymałościowe zostały spełnione, dlatego zostaję przy założonym module dla obu par kół m= 2,5mm

12. Obliczenia wytrzymałościowe wałków.

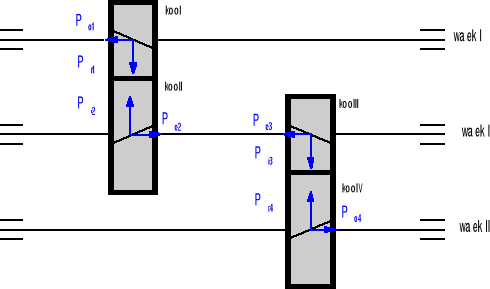
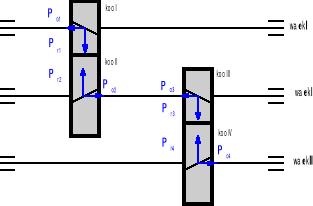
Schemat rozkładu sił w przekładni.

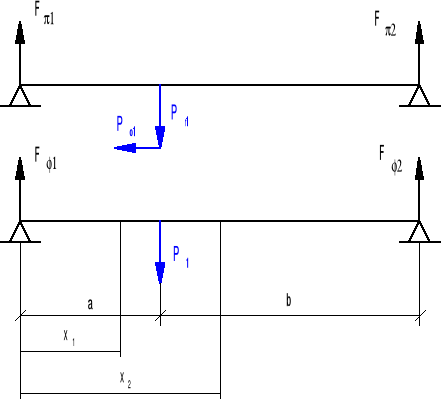
Obliczenia wałka pierwszego.

Wyliczam siły: promieniową P_r1 i poosiową P_o1 na podstawie wzorów:

gdzie:

• M₁ - moment obrotowy na pierwszym wałku,

• d_p1 - średnica podziałowa pierwszego koła,

• P_r1 - siła promieniowa,

• P_o1 - siła poosiowa,

• α - kąt linii przyporu,

• β - kąt pochylenia linii zęba.

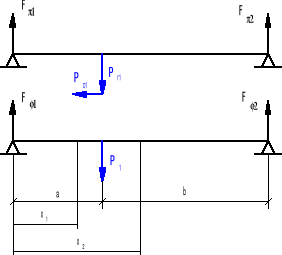
Rozpatruję wałek w płaszczyźnie Π.

F_Π1=166,8 N F_Π2=116,1 N

Momenty gnące:

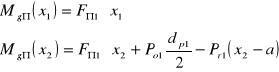
dla x₁= 0 M_gΠ1= 0

x₁= a M_gΠ1= 6,68 Nm

x₂=a M_gΠ2= 10,22 Nm

x₂=a+b M_gΠ2= 0

Rozpatruję wałek w płaszczyźnie Φ.

F_Φ1=516 N F_Φ2=234,7 N

Momenty gnące:

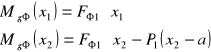
dla x₁= 0 M_gΦ1= 0

x₁= a M_gΦ1= 20,66 Nm

x₂=a M_gΦ2= 20,66 Nm

x₂=a+b M_gΦ2= 0

Obliczam reakcje występujące w łożyskach:

= 542 N
= 261,8 N

Obliczam wypadkowy moment gnący:

M_g1 = M_g3 = 0 M_g2=23,04 Nm

Obliczam moment zastępczy:

M_z1 = 11,45 Nm M_z2 = 25,73 Nm M_z3 = 0

Wyliczam średnice wałka:

Wałek będzie wykonany ze stali 35 dla której dopuszczalne naprężenia na zginanie wynoszą : k_gj = 110 MPa

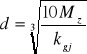
d₁ = 10,13 mm d₂ = 13,27 mm

gdzie:

• M_s - moment skręcający,

k_gj - dopuszczalne naprężenia na zginanie materiału wałka

Przyjmuję średnice pod łożyska równą 17 mm

Przyjmuję średnicę pod koło zębate nr I równą 27mm

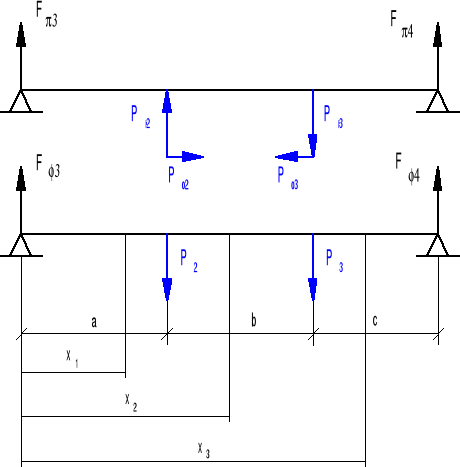
Obliczenia wałka drugiego.

a = 40mm; b = 44mm; l = a+b+c; l = 128mm

Wyliczam siły:

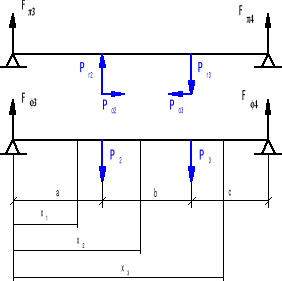
Rozpatruję wałek w płaszczyźnie Π.

F_Π3=116,18 N F_Π4=503,44 N

Momenty gnące:

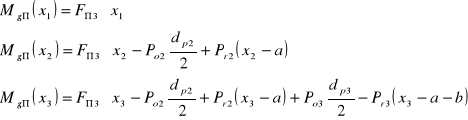
dla x₁= 0 M_gΠ1= 0

x₁= a M_gΠ2= 4,65 Nm

x₂=a M_gΠ2= -9,45 Nm

x₂=a+b M_gΠ3= 8,05 Nm

x₃=a+b M_gΠ3= 22,15 Nm

x₃=a+b+c M_gΠ4= 0

Rozpatruję wałek w płaszczyźnie Φ.

F_Φ3=1336,3 N F_Φ4=1803,5 N

Momenty gnące:

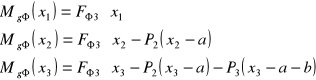
dla x₁= 0 M_gΦ1= 0

x₁= a M_gΦ2= 53,45 Nm

x₂=a M_gΦ2= 53,45 Nm

x₂=a+b M_gΦ3= 79,36 Nm

x₃=a+b M_gΦ3= 79,36 Nm

x₃=a+b+c M_gΦ4= 0

Obliczam reakcje występujące w łożyskach:

Obliczam wypadkowy moment gnący:

M_g1 = 0 M_g2 = 54,28 Nm M_g3 = 82,39 Nm M_g4 = 0

Obliczam moment zastępczy:

M_z1 = 0 Nm M_z2 = 70,88 Nm M_z3 = 94,16 Nm M_g4 = 0

Wyliczam średnice wałka:

Wałek będzie wykonany ze stali 35 dla której dopuszczalne naprężenia na zginanie wynoszą : k_gj = 110 MPa

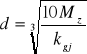
d₂ = 18,60 mm d₃ = 25,44 mm

Przyjmuję średnice pod łożyska równą 35 mm

Przyjmuję średnicę pod koło zębate nr II równą 45mm

Przyjmuję średnicę pod koło zębate nr III równą 45mm

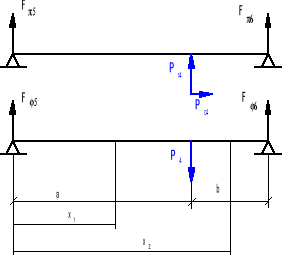
Obliczenia wałka trzeciego.

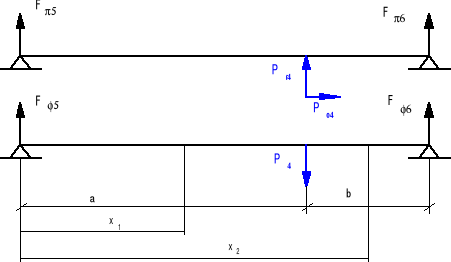
Wyliczam siły:

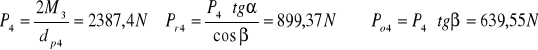
Rozpatruję wałek w płaszczyźnie Π.

F_Π4=188,72 N F_Π5=-1088,0 N

Momenty gnące:

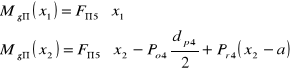
dla x₁= 0 M_gΠ1= 0

x₁= a M_gΠ2= 15,85 Nm

x₂=a M_gΠ2= -47,8 Nm

x₂=a+b M_gΠ3= 0

Rozpatruję wałek w płaszczyźnie Φ.

F_Φ5=820,63 N F_Φ6=1566,6 N

Momenty gnące:

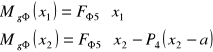
dla x₁= 0 M_gΦ1= 0

x₁= a M_gΦ2= 68,93 Nm

x₂=a M_gΦ2= 68,93 Nm

x₂=a+b M_gΦ3= 0

Obliczam reakcje występujące w łożyskach:

Obliczam wypadkowy moment gnący:

M_g1 = 0 M_g2 = 70,73 Nm M_g3 = 0

Obliczam moment zastępczy:

M_z1 = 0 Nm M_z2 = 217,8 Nm M_z3 = 206 Nm

Wyliczam średnice wałka:

Wałek będzie wykonany ze stali 35 dla której dopuszczalne naprężenia na zginanie wynoszą : k_gj = 110 MPa

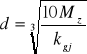
d₂ = 27,03 mm d₃ = 26,53 mm

Przyjmuję średnice pod łożyska równą 30 mm

Przyjmuję średnicę pod koło zębate nr IV równą 40mm

13. Obliczenia łożysk.

Przyjmuję trwałość łożysk pracy będzie wynosić 5000 godzin

Ze względów konstrukcyjnych dla każdego wałka dobieram łożyska stożkowe

Obliczam obciążenie zastępcze:

P_I = R₁ = 542,70 N P_II = R₂ = 1872,5 N P_III = R₃ =1907,4 N

gdzie:

• P - obciążenie zastępcze,

• X, Y - współczynniki obciążenia poprzecznego i wzdłużnego,

• R - reakcja w łożysku,

• F_o - siła poosiowa,

Obliczam nośność ruchową:

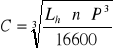
C_I = 6730 N C_II = 14640 N C_III = 9024 N

gdzie:

• C - nośność ruchowa,

• L_h - trwałość łożyska w godzinach pracy,

• n - prędkość obrotowa łożyska,

• P - obciążenie zastępcze.

14. Dobór łożysk na podstawie PN - 86/M - 86220.

- dla wałka pierwszego jednorzędowe łożyska stożkowe serii 30203, dla których nośność ruchowa wznosi 13500 N

- dla wałka drugiego jednorzędowe łożyska stożkowe serii 30207, dla których nośność ruchowa wznosi 36000 N

- dla wałka trzeciego jednorzędowe łożyska stożkowe serii 30206, dla których nośność ruchowa wznosi 27500N

15. Obliczenia wpustów pod koła zębate.

Obliczam siłę działającą na wpust:

gdzie:

• F - siła działająca na wpust,

• M - moment obrotowy,

• d - średnica wałka.

pod koło zębate nr I do średnicy wałka 27 mm wpust b x h; 8 x 7

pod koło zębate nr II do średnicy wałka 45 mm wpust b x h; 14 x 9

pod koło zębate nr III do średnicy wałka 45 mm wpust b x h; 14 x 9

pod koło zębate nr IV do średnicy wałka 40 mm wpust b x h; 12 x 8

Na podstawie PN - 70/M - 85005 dla danej średnicy dobieram wpust b×h.

Obliczam długość wpustu:

Zakładam, że wszystkie wpusty będą wykonane ze stali St7, dla której dopuszczalne naprężenia wynoszą; k_o = 105 MPa

Wyliczona długość wpustu pod koło nr I wynosi: 10,33mm , przyjmuję: 15mm

Wyliczona długość wpustu pod koło nr II wynosi: 18,05mm , przyjmuję: 20mm

Wyliczona długość wpustu pod koło nr III wynosi: 18,05mm , przyjmuję: 20mm

Wyliczona długość wpustu pod koło nr IV wynosi: 34,66mm , przyjmuję: 35mm

gdzie:

• l - długość wpustu,

• b - szerokość wpustu,

• l_o - czynna długość wpustu,

• F - siła działająca na wpust,

• t - wysokość rowka na wpust,

• k_o - naciski dopuszczalne,

• z - współczynnik zależny od warunków pracy,

• k_c - dopuszczalne naprężenia na ścinanie.

16. Obliczenia na zagrzanie przekładni.

Obliczam moc tarcia.

N_t = 0,18 kW

gdzie:

• N_t - moc tarcia,

• N_t1, N_t2 - moc tarcia pierwszej i drugiej pary kół zębatych,

• N - moc przenoszona przez przekładnię,

• i₁, i₂ - przełożenie pierwszej i drugiej pary kół zębatych,

• z₁, z₃ - liczba zębów koła pierwszego i trzeciego.

Sprawdzam czy warunek przed nadmiernym zagrzaniem jest spełniony:

x_t = 2,97 > 1

gdzie:

• x_t - współczynnik pewności,

• m - moduł koła zębatego,

• b - szerokość wieńca zębatego.

---