Temat: Wyznaczanie logarytmicznego dekrementu tłumienia

Numer pary: 7

Numer ćwiczenia: 72

I Opis teoretyczny

1. Ruch drgający

II zasada dynamiki Newtona ruchu drgającego harmonicznie ma postać

(2)

Gdzie:

F_s - siła „sprężysta”

Wartość siły jest wprost proporcjonalna do wychylenia x i do siły kierującej k, możemy ją zatem określić wzorem:

(1)

F_s=-kx

zatem

Znak minusa we wzorze (1) pochodzi stąd, że siła F_s ma zawsze zwrot przeciwny do zwrotu wychylenia. Korzystając z definicji przyśpieszenia:
oraz ze wzoru (1) równanie (2) przybiera postać:

(3)

Jest to równanie różniczkowe ruchu harmonicznego. Drgania harmoniczne, nietłumione i niezłożone opisuje kinematyczne równanie ruchu drgającego:

(4)

Gdzie:

x - wychylenie od środka drgań

- pulsacja lub częstotliwość cykliczna

Gdzie:

v-częstotliwość (liniowa),

T- okres drgań.

Z równań (3) i (4) wynika, że

Pulsacja zależy więc od masy ciała wykonującego drgania oraz od współczynnika k charakteryzującego pole siły, dzięki którym drgania zachodzą, stąd
można nazwać pulsacją drgań własnych.

Jedną z całek równania (4) jest funkcji:

x=Acos
t

Gdzie:

1. Maksymalne wychylenia, zwane amplitudą

Łatwo stąd obliczyć przyśpieszenie ruchu harmonicznego a_h:

(5)

a_h=-A
²cos
t

lub

a_h=-
²x

czyli a_h jest proporcjonalne do wychylenia x.

Ze wzoru (5) wynika że przyśpieszenie jest kosinusoidalną lub sinusoidalną funkcją

czasu, prędkość w tym ruchu:

2. Ruch drgający tłumiony

Z reguły, a w drganiach mechanicznych, siła sprężysta nie jest jedyną siłą występującą w tym ruchu. Towarzyszy jej zawsze siła utrudniająca ten ruch, zwana siłą tłumiącą, drgania zaś nazywamy drganiami harmonicznymi tłumionymi. Częstym przypadkiem sił tłumiących są siły, których wartość jest wprost proporcjonalna do prędkości ruchu ν, np. siła oporu F_t, jakiego doznaje kulka poruszająca się w ośrodku lepkim.

lub

Gdzie:

b- współczynnik oporu

We wzorze Stokesa b=6πηr

η - współczynnik lepkości

r - promień kulki

Znak minusa wynika stąd, że siła oporu ma zawsze przeciwny zwrot do zwrotu wektora prędkości. Obie siły (siła sprężysta F_s i siła tłumiąca F_t ) działają w każdej chwili wzdłuż tej samej prostej, dlatego ich wypadkową można znaleźć przez algebraiczne dodanie.

Czyli według drugiej zasady Dynamiki Newtona:

lub

Przenosimy wszystkie wyrazy na jedną stronę i dzielimy przez masę m:

Wprowadzamy oznaczenie: (7)

i otrzymujemy ostatecznie: (8)

Jest to równanie różniczkowe ruchu harmonicznego tłumionego. Zakładamy, że

drgania odbywają się wzdłuż osi OX. Czyli: (9)

lub

Poleca się sprawdzenie czy powyższa funkcja spełnia równanie (7) używając pochodnych:

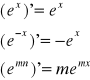
Gdzie:

x - wychylenie od położenia równowagi

A₀ - początkowa, maksymalna amplituda

e - podstawa logarytmu naturalnego

δ - współczynnik zwany stałą tłumienia

ω - pulsacja rozpatrywanego ruchu tłumionego

(ω_t + φ) - faza ruchu

φ - faza początkowa tzn. dla t=0 (10)

Więc pulsacja drgań tłumionych jest mniejsza od pulsacji drgań nietłumionych, a tym samym okres jest dłuższy T > T₀ .

to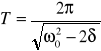
, podczas gdy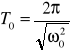

Wartość okresu T jest w danym ruchu jest stała (podobnie T₀ ). Podczas określania warunku rezonansu należy uwzględnić wzór (9). Czyli:

czyli gdy

W ośrodkach o dużym współczynniku oporu b, a tym samym dużej stałej tłumienia δ może wystąpić relacja przeciwna:

Analizując wzór (8) czynnik sin(ωt+δ) wskazuje, że jest to ruch okresowo zmienny, tak jak funkcja sinusa, a więc jest to ruch drgający harmoniczny. Czynnik
jest wyrażeniem określającym amplitudę tego ruchu, możemy więc napisać:

(11)

Ze wzoru (10) wynika, że amplituda A ruchu tłumionego maleje z upływem czasu w sposób wykładniczy do zera, tym szybciej, im większa jest wartość δ. Wykresem funkcji (9), czyli ruchu harmonicznego tłumionego, jest malejąca sinusoida (założenie
). Spadek amplitudy w rozpatrywaniu ruchu drgającego tłumionego wykazuje prawidłowość, polegająca na tym, że stosunek dwóch kolejnych amplitud dla wychyleń w tę samą stronę ma stałą wartość, np.:

3. Dekrement logarytmiczny tłumienia jest to logarytm naturalny dwóch kolejnych

wartości amplitud, z których druga następuje po pierwszej w odstępie czasu równym okresowi T.

lub

stąd (12)

Gdzie:

- logarytm naturalny

- amplituda drgań

- stała tłumienia

t - czas

T - okres drgań

O ile stała tłumienia
, zwana też wykładnikiem tłumienia, określa zmniejszenie się amplitudy w czasie jednej sekundy, o tyle dekrement tłumienia określa zmniejszenie się amplitudy w czasie jednego okresu T, co jest ogólniejsze i bardziej precyzyjne, gdyż jedna sekunda w wielu przypadkach jest odstępem czasowym tak długim, że mieszczą się w nim tysiące, a nawet miliony drgań a ściślej miliony okresów.

Jeżeli dwie kolejne amplitudy A₁ i A₂ można zmierzyć bezpośrednio, to na podstawie definicji można obliczyć dekrement tłumienia:

II Opis ćwiczenia

Wykonanie pomiaru:

1. Płytkę P wychylić o pewien kąt, puścić swobodnie i obserwować wahania układu. Gdy zgasną dodatkowe drgania poprzeczne, a jednocześnie kąt wychyleń układu zmaleje do wartości ok. 20˚, zmierzyć stoperem czas kilkunastu drgań („wahnięć”) t_n.

2. Obliczy okres drgań
   ; n - liczba drgań.

3. Uruchomić układ ponownie i odczytywać na przymiarze milimetrowym kolejne wartości amplitud A₁, A₂, A₃, …, z jednej strony od położenia równowagi S.

4. Czynności 1, 2, 3 powtórzyć kilka razy, zawsze przy takim samym wychyleniu początkowym A₀, i obliczyć wartości średnie
   _n,
   oraz wartości średnie poszczególnych amplitud
   ₁,
   ₂,
   ₃, …

5. Sporządzić na papierze milimetrowym wykres A od t, odkładając na osi rzędnych wartości kolejnych amplitud
   ₀,
   ₁,
   ₂, …,
   _n, a na osi odciętych czas, przyjmując za jednostkę czasu obliczony średni okres wahań
   .

6. Obliczyć dekrement tłumienia Λ, biorąc wartości [A_n, A_n+1] ze sporządzonego wykresu w kilku dowolnych miejscach odpowiadających odstępowi czasu T, np. dla punktów C₁ i C₂.

7. Ze wzoru (3) obliczyć Λ dla kilku „sąsiednich” amplitud średnich, np.

,
,
, …,

Obliczyć średnią wartość

i porównać z wartością Λ otrzymaną w pkt. 6.

8. Ze wzoru (12) obliczyć δ (biorąc
   ).

9. Ze wzoru (7) obliczyć b (masa jest podana przy ćwiczeniu).

10. Wyniki umieścić w tabelkach.

11. Przeprowadzić dyskusję błędów

Nr pomiaru		n
I pomiar
II pomiar
III pomiar
	=

Nr pomiaru
I pomiar
II pomiar
III pomiar
Średnie wartości amplitud

Wyprowadzenie wzoru na niepewność standardową:

7

---