POLITECHNIKA KOSZALIŃSKA

KATEDRA MECHANIKI TECHNICZNEJ

I WYTRZYMAŁOŚCI MATERIAŁÓW

LABORATORIUM MECHANIKI

Temat: Wyznaczanie środka ciężkości brył o nieregularnym rozkładzie masy.

Opracował:

dr. inż. M. Fligiel

Koszalin 2005

1. CEL ĆWICZENIA

Celem ćwiczenia jest zapoznanie studentów z teorią środka ciężkości oraz zweryfikowanie teorii z praktycznym sposobem wyznaczania środka ciężkości brył o nieregularnie rozłożonej masie.

2. WSTĘP

Siły przyciągania ziemskiego pojedynczych cząstek ciała skierowane są w przybliżeniu do środka Ziemi. Ponieważ rozmiary ciał w porównaniu z rozmiarami Ziemi są małe, to przyjmujemy, że siły te są równoległe. Wypadkowa tych sił jest siłą ciężkości ciała, natomiast punkt przyłożenia wypadkowej sił przyciągania ziemskiego pojedynczych cząstek jest środkiem ciężkości ciała.

W ciałach stałych środek ciężkości zajmuje zawsze ściśle określone położenie, które nie zależy od położenia ciała w przestrzeni.

Wyznaczanie środka ciężkości jest jednym z ważniejszych zagadnień statyki. Znajomość położenia środka ciężkości wpływa na prawidłowy wybór podpór i obciążeń w konstrukcji.

Przy konstruowaniu urządzeń należy kierować się zasadą: ciało (układ ciał) pozostaje w stanie niezmiennym, jeżeli linia działania wypadkowej sił ciężkości nie wychodzi poza podstawę ciała.

Położenie środka ciężkości stanowi o równowadze i możliwościach manewrowych takich maszyn jak dźwigi, koparki, wysięgarki itp.

3. WPROWADZENIE TEORETYCZNE

a) Wypadkowa i środek sił równoległych

Przed przystąpieniem do określenia położenia środka ciężkości, przypomnijmy sobie podstawowe wiadomości z zakresu redukcji sił równoległych.

Rys.1

Załóżmy, że do ciała w punktach
,
,
,... ,
przyłożone są siły równoległe
,
,
skierowane są w jedną stronę, a siły
,
w stronę przeciwną (rys. 1). Sił równoległych w ogólnym przypadku może być nieskończenie wiele.

Zsumujmy siły
,
. Zgodnie z zasadami statyki otrzymamy:

=
+
(1)

=


. (2)

Równanie (1) określa moduł wypadkowej sił
,
, a równanie (2) położenie punktu
przyłożenia siły wypadkowej
.

Dalej, zsumujmy siłę
i
. Otrzymamy wówczas siłę wypadkową

=
+
, (3)

a punkt przyłożenia tej siły określimy zgodnie z równaniem

=


. (4)

Analogicznie określimy wypadkową sił
i
, oraz jej punkt przyłożenia
:

=
+
(5)

=


(6)

W rezultacie otrzymaliśmy dwie siły
i
przeciwnie skierowane i przyłożone w punktach
i
.

W zależności od modułów tych dwóch sił (siły
i
są przeciwnie skierowane) i ich punktów przyłożenia rozróżniamy następujące przypadki:

1. Moduły sił
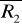
   i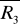
   nie są równe.

Załóżmy, że
>
, wówczas wypadkowa sił jest równa

=
-
(7)

i skierowana jest w stronę większej siły, a punkt C (rys. 1) przyłożenia siły
określimy na podstawie równania:

=


. (8)

Punkt C przyłożenia wypadkowej sił równoległych nazywa się środkiem sił równoległych.

Przez ten punkt będzie zawsze przechodziła linia działania wypadkowej
sił
,
, ... niezależnie od tego o jaki kąt
(jednakowy dla wszystkich sił
,
,...) obrócimy wszystkie siły.

2. Siły
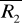
   i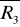
   równe są co do modułu i linie działania ich nie pokrywają się.

3. Siły
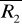
   i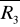
   równe są co do modułu i linie ich działania pokrywają się. W tym przypadku siły wzajemnie równoważą się.

W przypadku gdy siły
i
posiadają takie same zwroty (skierowane są w jedną stronę) wówczas wypadkowa tych sił jest zawsze siłą. Siły te nie mogą równoważyć się, a także nie mogą redukować się do pary sił.

b) Współrzędne środka sił równoległych. Środek ciężkości.

Rozpatrzmy układ sił równoległych
,
,...,
,...,
, gdzie
, przyłożonych w punktach
,
,...,
(rys. 2). Siły
,
,...,
,...,
, są siłami przyciągania ziemskiego pojedynczych cząstek ciała.

Położenie środka C sił równoległych, określa się jego promieniem-wektorem
względem początku układu współrzędnych O lub trzema współrzędnymi
,
,
z końca wektora
.

Rys. 2

Zgodnie z zasadami statyki, wypadkową sił możemy określić przyrównując jej moment względem dowolnego punktu (np. początku układu współrzędnych O) z sumą momentów poszczególnych sił względem tego samego punktu. Na podstawie powyższego napiszemy:

(9)

lub

(10)

gdzie
- wypadkowa sił przyciągania ziemskiego, ciężar ciała.

Wprowadźmy wektor jednostkowy
równoległy do linii działania sił
.

Wówczas otrzymamy:

(11)

i

(12)

lub w zapisie algebraicznym

(13)

gdzie
- moduł wektora
.

Położenie środka sił ciężkości określimy z równania sił momentów elementarnych sił
. Równanie momentów, zgodnie z (10), (11) i (12) będzie następujące:

(14)

lub po przekształceniu

(15)

(16)

Wektor jednostkowy
może mieć dowolny kierunek, gdyż zgodnie z teorią sił równoległych linie działania sił równoległych można obracać o ten sam kąt
. Obrót o kąt
nie wpływa na zmianę siły wypadkowej.

W związku z powyższym, aby spełnione było równanie (16) część równania w nawiasie musi być równa 0:

(17)

skąd

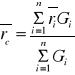
(18)

Rzutując wektory lewej i prawej części równania (18) na osie układu współrzędnych otrzymamy współrzędne środka ciężkości:

,
,
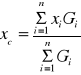
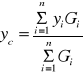
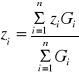
(19)

Środkiem ciężkości nazywamy punkt C
, przez który zawsze przechodzi linia działania wypadkowej sił równoległych, niezależnie od obrotu tych sił o dowolny (ale ten sam dla wszystkich sił) kąt
wokół ich punktu zaczepienia (rys. 2).

Wyrażenia w liczniku wzorów (19)

,
,
(20)

są momentami statycznymi względem płaszczyzny
,
,
.

Jeżeli przyjmiemy, że
, gdzie
jest masą i-tej cząstki, g przyspieszeniem ziemskim, to otrzymamy:

,
,
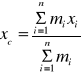
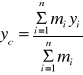
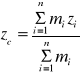
(21)

Z powyższych wzorów wynika, że środek ciężkości ciał jednorodnych pokrywa się ze środkiem masy.

Do wyznaczenia środka ciężkości stosować można następujące metody:

Metoda rozbicia polega na tym, że daną bryłę (figurę płaską lub linię) rozbijamy myślowo na elementy proste, których współrzędne środków ciężkości są znane (np.: stożek, prostopadłościan, prostokąt, trójkąt, itd.), następnie zaczepiamy w tych środkach ciężkości siły proporcjonalne do objętości, pól powierzchni lub długości linii tych elementów i stosujemy podane wyżej wzory, wyznaczając:

• dla bryły, przestrzennej płaszczyzny i linii
  ;

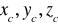
• dla figury płaskiej
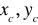
  (figura leży w płaszczyźnie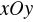
  );

• dla linii prostej
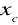
  (linia pokrywa się z osią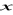
  ).

Metoda dopełnienia polega na tym, że do figury z wycięciami lub otworami dodajemy pewne figury, otrzymując w ten sposób ciało najczęściej symetryczne, w każdym razie o znanych współrzędnych środków ciężkości.

Metodę całkowitą stosuje się w przypadku, gdy figura płaska jest na tyle regularna, że nie można zastosować żadnej z wymienionych wyżej metod. Wówczas współrzędne środków ciężkości określimy ze wzorów:

• dla bryły:

,
,

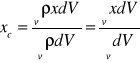
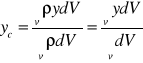
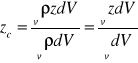
(22)

gdzie
- ciężar właściwy bryły,
- objętość;

• dla figury płaskiej:

,

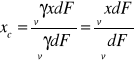
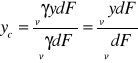
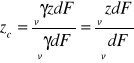
(23)

gdzie
- ciężar przypadający na jednostkę powierzchni figury,
- jej powierzchnia;

• dla linii krzywej przestrzennej;

,

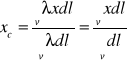
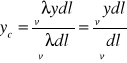
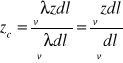
(24)

gdzie
- ciężar przypadający na jednostkę długości linii,
- jest długością linii.

Twierdzenia wykorzystywane przy określaniu środka ciężkości:

1. Jeżeli jednorodne ciało posiada oś symetrii, to środek ciężkości znajduje się na tej osi.

2. Jeżeli jednorodne ciało posiada płaszczyznę symetrii, to środek ciężkości znajduje się na tej osi.

Na podstawie powyższych dwóch twierdzeń określimy środki ciężkości niektórych symetrycznych figur:

1. Środek ciężkości powierzchni równoległościanu, rombu, prostokąta i kwadratu leży w punkcie przecięcia się ich przekątnych.

2. Środek ciężkości powierzchni prawidłowego wielokąta znajduje się w środku opisanego lub wpisanego w nim koła.

3. Pierwsza reguła Guldina:

Pole powierzchni bryły otrzymanej przez obrót krzywej płaskiej dookoła osi, leżącej w płaszczyźnie krzywej nie przecinającej tej krzywej równa się iloczynowi długości tej krzywej przez drogę jaką opisuje jej środek ciężkości (rys. 3):

(25)

gdzie
- pole powierzchni bocznej,
- długość krzywej płaskiej danej równaniem
,
- współrzędna środka ciężkości krzywej.

Rys. 3

4. Druga reguła Guldina:

Objętość bryły otrzymanej przez obrót obszaru płaskiego (zakreskowanego) dookoła osi leżącej w płaszczyźnie obszaru i nie przecinającej go równa się iloczynowi pola obszaru przez drogę jaką przebył środek ciężkości obszaru:

(26)

gdzie
- objętość bryły,
- współrzędna środka ciężkości obszaru płaskiego (zakreskowanego),
- pole obszaru płaskiego.

Dowody powyższych twierdzeń czytelnik może znaleźć w dowolnej literaturze dotyczącej mechaniki ogólnej.

W tablicy I zestawiono wzory na współrzędne środków ciężkości podstawowych figur i brył geometrycznych.

4. PRZEBIEG ĆWICZENIA

Eksperymentalne wyznaczanie środka ciężkości przeprowadzimy dla bryły pokazanej na rys. 4.

Rys. 4

Płyta, której konfigurację możemy zmieniać dokładając lub odejmując poszczególne jej elementy, ustawiona jest na trzech wypoziomowanych czujnikach służących do określenia sił reakcji. Wartość tych sił mierzymy przy pomocy mostka tensometrycznego. Przed przystąpieniem do pomiaru siły, mostek należy wyzerować i wyskalować. Skalowanie mostka dokonujemy ciężarkiem o znanej masie.

Aby eksperymentalnie wyznaczyć współrzędne środka ciężkości
(3 niewiadome) należy:

1. Wyznaczyć masę
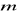
   i ciężar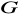
   płyty.

2. Dokonać pomiaru sił reakcji
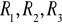
   dla położenia poziomego płyty.

3. Napisać równania równowagi momentów:

,
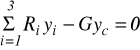
(27)

gdzie
- współrzędne położenia opór.

Moment względem osi
jest równy 0, gdyż zgodnie z zasadami statyki

(28)

gdzie
,
.

W związku z powyższym, aby określić współrzędną
musimy napisać dodatkowe równanie.

Rys. 5

,

4. Dokonać pomiaru sił reakcji
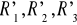
   dla płyty obróconej o pewien kąt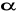
   (rys. 5).

Przy obrocie płyty o kąt
pojawią się składowe
,
.

5. napisać dodatkowe równanie momentów, np. względem osi
   

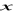
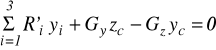
(30)

i wyznaczyć z niego brakującą współrzędną środka ciężkości
. Wyznaczone w powyższy sposób współrzędne należy porównać ze współrzędnymi wyznaczonymi teoretycznie.

6. SPRAWOZDANIE

Sprawozdanie z ćwiczenia powinno zawierać:

• cel ćwiczenia

• krótkie wprowadzenie teoretyczne

• przebieg eksperymentu

• rysunki i teoretyczne obliczenia współrzędnych środka ciężkości

• rysunki i obliczenia współrzędnych środka ciężkości na podstawie eksperymentu]

• wnioski

7. LITERATURA

1. J. Nzioł, Metodyka rozwiązywania zadań z mechaniki. PWN , Warszawa, 1980

2. A. A. Jabłonskij, Kurs tieoreticzeskoj miechaniki, Wysszaja Szkoła, Moskwa, 1967

Figura	Współrzędne środka ciężkości
prosta
część łuku
prostokąt
trójkąt
trapez
wycinek koła
prostopadłościan
stożek
półkula

Tablica I

10

Z

Y

Z

Z

Z

Z

Z

Z

Z

Z

C

C

C

C

C

C

C

C

l

R

2α

a

b

b

a

a/2

b/2

R

2α

X_c

Y_c

Z_c

h

R

linia

działania

wypadkowej

A₄

B₃

A₅

A₁

B₁

B₂

A₃

P₄

R₃

P₅

C

P₁

R₁

R₂

P₂

R

P₃

X

Y

Z

Y_c

Y_c

X_i

X_c

Z_i

Z_c

i

j

k

u

0

A₀

G₀

φ

φ

φ

φ

A₁

A_i

C

G₁

G

G_i

r_i

r_i

linia działania wypadkowej

X

Y

Z

y_C

Z_c

r

F₀

Y=Y(X)=l

F_b

V

x

y

z

A₁

A₂

A₃

1

2

3

R₁

R₂

R₃

C

G

z_c

x_c

y_c

x₁

y₁

x

y

z

A₁

A₂

A₃

R'₁

R'₂

R'₃

α

α

α

α

G

G_y

G_z

z_c

Y_c

x_c

---