1.Jaki układ mechaniczny nazywamy układem statycznie niewyznaczalnym, narysuj przykład takiego układu.

Układ statycznie wyznaczalny (izostatyczny) to taki, w którym liczba możliwych do ułożenia równań równowagi równa jest liczbie niewiadomych.

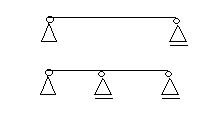
W mechanice teoretycznej zajmujemy się tylko układami statycznie wyznaczalnymi.

3. Momentem siły względem prostej (osi) z nazwiemy moment rzutu siły F na płaszczyznę prostopadłą do osi z, względem punktu O, w którym oś przebija wspomnianą płaszczyznę.

M=r x P

4.Tarcie ślizgowe - ciała sztywnego o pow. płaską

Przyczyną tarcia jest chropowatość powierzchni ciał, które pod wpływem obciążeń zewn. wykazują tendencje doprzesuwania się względem siebie.

Największą wartość siły F, która nie naruszy jeszcze stanu względnego spoczynku jest równa tzw. rozwinietej siły tascia statycznego:

T=μ*N

Prawa tacia:

a) ciała tarcia nie zależy od wielkości stykajacych się powierzchni, ale od ich rodzaju.

b) watrość siły tarcia w spoczynku może zmieniać wartość od 0 do wartości maksymalnej, proporcjonalnej do całkowitego nacisku normalnego.

c) w przypadku, gdy ciało ślizga się po pewnej powierzchni siła tarcia jest zawsze skierowana przeciwnie do kietunku ruchu. W momencie ruchu jest mniejsza od maksymalnej wartości sily tarcia spoczynkowego.

5.Prędkosć i przyspieszenie bryły w ruchu obrotowym.

Pierwszą pochodną kąta obrotu względem czasu nazywamy prędkością kątową ruchu obrotowego. Prędkość kątowa to wektor leżący na osi obrotu ciała. Zwrot wyznaczamy z reguły śruby prawoskrętnej biorąc pod uwagę kierunek obrotów.

Moduł wektora prędkości kątowej wynosi:

Każdy punkt obracającej się bryły ma inną prędkość liniową, natomiast prędkość kątowa wszystkich punktów bryły jest taka sama. Punkt odległy od osi obrotu o r ma prędkość liniową v taką, że

Rozkład prędkości punktów

Należy pamiętać, że wektor prędkości kątowej jest prostopadły do płaszczyzny ruchu. Przyspieszenie kątowe

Drugą pochodną kąta obrotu nazywamy przyspieszeniem kątowym ruchu obrotowego. Przyspieszenie kątowe to wektor leŜący na osi obrotu ciała. Zwrot zgodny ze zwrotem wektora prędkości kątowej gdy ruch jest przyspieszony lub zwrot przeciwny do zwrotu wektora prędkości kątowej gdy ruch jest opóźniony.

Moduł wektora przyspieszenia kątowego wynosi:

Każdy punkt obracającej się bryły ma inne przyspieszenie liniowe, natomiast przyspieszenie kątowe wszystkich punktów bryły jest takie samo. Punkt odległy od osi obrotu o r ma przyspieszenie liniowe a takie, że

Należy pamiętać, że wektor przyspieszenia kątowego jest prostopadły do płaszczyzny ruchu.

6.Definicja ruchu płaskiego.

Ruchem płaskim ciała sztywnego (bryły materialnej) nazywamy taki ruch podczas którego wszystkie punkty ciała poruszają się w płaszczyznach równoległych do pewnej nieruchomej płaszczyzny zwanej płaszczyzną kierującą.

Ruch płaski bryły sztywnej można przedstawić:

- jako przemieszczenie i obrót

- jako obrót wokół szczególnego punktu

Ruch płaski jako złożenie przemieszczenia i obrotu:

Równania:

xA=xA(t) xB=xB(t)

yA=yA(t) yB=yB(t)

Ruch obrotowy:

7.Prędkosć liniowa, przyspieszenie liniowe punktu bryły sztywnej w ruchu złożonym

Wielkości kinematyczne to wielkości występujące w kinematyce: tor, prędkość, przyspieszenie, droga.

Wielkości kinematyczne bezwzględne to wielkości kinematyczne dotyczące poruszającego się punktu P odniesione do stałego układu odniesienia.

Wielkości kinematyczne względne to wielkości kinematyczne dotyczące poruszającego się punktu P odniesione do ruchomego układu odniesienia

Wielkości kinematyczne unoszenia to wielkości kinematyczne przynależne temu punktowi ruchomego układu odniesienia, który w danej chwili pokrywa się z punktem P. Inaczej mówiąc są to wielkości opisujące ruch układu ruchomego względem nieruchomego.

W ruchu złożonym punktu prędkość bezwzględna punktu jest sumą geometryczną wektorów prędkości względnej i prędkości unoszenia.

lub uogólniając oznaczenia

V_b - prędkość bezwzględna (prędkość punktu P względem układu nieruchomego)

V_w - prędkość względna (prędkość punktu P względem układu ruchomego)

V_u - prędkość unoszenia, czyli prędkość punktu tego punktu układu ruchomego (obliczana względem układu nieruchomego), z którym w danej chwili pokrywa się ruchomy punkt P.

Zazwyczaj prędkości względna i unoszenia nie są wzajemnie prostopadłe

Moduł wektora prędkości bezwzględnej wyznaczamy w takim przypadku z następującej zależności:

Przyspieszenie punktu

Przyspieszenie punktu wyrażamy jako pochodną wektora prędkości

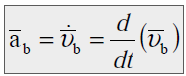
W ruchu złożonym przyspieszenie punktu jest sumą geometryczną (wektorową) przyspieszenia względnego, przyspieszenia unoszenia i przyspieszenia Coriolisa.

a_b - przyspieszenie bezwzględne czyli przyspieszenie punktu P względem nieruchomego układu odniesienia

a_u - przyspieszenie unoszenia czyli przyspieszenie punktu układu ruchomego z którym w danej chwili pokrywa się punkt P

a_w - przyspieszenie względne, czyli przyspieszenie punktu P względem układu ruchomego

Przyspieszenie Coriolisa Określa wpływ ruchu względnego na ruch unoszenia i odwrotnie

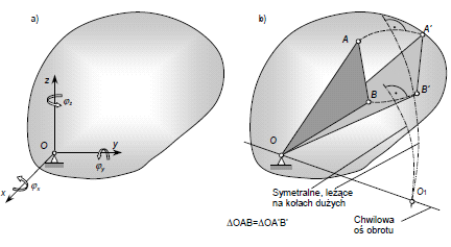
8.Na czym polega precesja regularna w ruchu kulistym.

Ruchem kulistym nazywamy, ruch ciała sztywnego, którego jeden punkt, zwany środkiem ruchu kulistego, jest unieruchomiony.

Precesja regularna - ruch kulisty ciała sztywnego, który charakteryzuje się tym, że kąt nutacji jest stały, a prędkości obrotu własnego i precesji są stałe.

Wektor przyspieszenia kątowego jest prostopadły do płaszczyzny wyznaczonej wektorami oraz .

10.Twierdzenie Koeniga

Energia kinetyczna ciała sztywnego w ogólnym przypadku ruchu jest równa sumie energii kinetycznej ruchu postępowego z predkością równą prędkości środka masy i energii kinetycznej w ruchu obrotowym ciała względem jego środka masy.

E_k=1/2m*v₀+1/2J₁*ω²

J₁ - masowy moment bezwładności były wzgl. osi przechodzącej przez środek masy ciała

ω - prędkość kątowa

11.Zasada równowartości energii kinetycznej i pracy

Energia kinetyczna punktu materialnego rośnie lub maleje o wartość pracy wykonanej przez siły zewnętrzne działające na punkt materialny.

ΔE-E_k2-E_k1=L

Niech n1 będzie wartością bezwzględną prędkości w chwili początkowej t1, lewa strona równania wynosi więc:
, a prawa na podstawie wzoru równa się pracy, jaką wykonała siła F w czasie od t1 do t2, którą oznaczymy L. Równanie można więc napisać w postaci:

.

Wyrażenie
nazywamy energią kinetyczną punktu materialnego o masie m i prędkości
. Oznaczając

,
,

otrzymujemy:

.

Równanie opisuje tak zwaną zasadę równowartości energii kinetycznej i pracy. Zasada równowartości energii kinetycznej i pracy dla punktu materialnego.

Przyrost energii kinetycznej w pewnym przedziale czasu jest równy sumie sił zewnętrznych (czynnych i reakcji) działających w tym czasie.

Gdy praca sił działających jest równa zeru L = 0, wówczas na podstawie E2 - E1 = 0, czyli E2 = E1, więc zgodnie z E 2 =E1. Punkt ma prędkość stałą co do wartości. Jeżeli więc siła jest na przykład prostopadła do toru, to punkt porusza się ruchem jednostajnym. Przykładem  jest ruch jednostajny punktu materialnego po okręgu koła pod wpływem siły stałej co do wartości i skierowanej do środka koła.

12.Warunki zerowania się reakcji dynamicznych w ruchu obrotowym

13.Siły wewnętrzne w prętach płaskich

Pręty płaskie - leżą na płaszczyźnie (nie mają przekroju).

W prętach płaskich wyróżniamy jedynie siły wzdłużne , siły poprzeczne i moment gnący .

Aby wyznaczyć siły wewnętrzne należy dokonać myślowego przekroju i obliczyć siły i momenty dla jednej strony.

Siła normalna N jest równa sumie rzutów wszystkich sił działających na jedną część ciała (po jednej stronie przekroju) na kierunek normalny do przekroju.

Znak „+” jeŜeli siła działa od przekroju i pręt jest rozciągany. Znak „-” jeŜeli siła

działa do przekroju i pręt jest ściskany.

Siła tnąca T jest równa sumie rzutów wszystkich sił działających na jedną część ciała (po jednej stronie przekroju) na kierunek prostopadły do osi pręta.

Znak „+” jeŜeli siła jest skierowana „do góry”- po lewej stronie przekroju lub „w dół” po prawej stronie przekroju

Moment gnący M jest równy sumie momentów wszystkich sił działających na jedną część ciała (po jednej stronie przekroju) względem punktu, który jest środkiem przekroju. Za dodatnie przyjmujemy momenty wyginające belkę wypukłością w dół

14. Co to jest skrętnik

Układ złożony z jednej siły S równej wektorowi głównemu układu oraz z jednego wektora momentu Ms równoległego do tej siły nazywamy skrętnikiem lub śrubą układu sił.

W ogólnym przypadku przestrzenny dowolny układ sił możemy w jednoznaczny sposób zredukować do skrętnika.

15.Moment siły względem punktu.

Momentem siły względem punktu (nazwanego punktem „O”) wyrażony jest jako iloczyn wektorowy promienia wektora r i wektora siły F.

M^o = r x F

Zwrot M^o zgodny z regułą śruby prawoskrętnej.

Jego kierunek (M^o) jest prostopadły do płaszczyzny utworzonej przez wektory r i F.

Jego wartość jest równa |M^o|=Fd.

16.Tarcie toczne

Tarciem tocznym nazywamy opór toczenia ciała sztywnego w kształcie walca po pow. płaskiej.

Pod wpływem obciążeń czynnych F i Q następuje mikroodkształcenie w strefie kontaktu walca z podłożem.

Reakcja podłoża jest ukośna i rozkładamy ją na skladowe T₀ i N. Dla F=0 wyst. tylko reakcja pionowa N w punkcie A. Przy wzroście sily F następuje przesunięcie i pochylenie reakcji.

Równania równowagi:

F- T₀=0

N-Q=0

Q*f-F*R=0

Warunek toczenia

μ > f/r

Wielkość f określająca przesunięcie punktu A wzgl. B nazywamy współczynnikiem tarcia tocznego lub ramieniem oporu toczenia. Współczynnik tarcia tocznego f jest współczynnikiem wymiarowym [metr].

Po przekroczeniu punktu równowagi granicznej (F>F_g) ciało toczy się. Przesunięcie f występuje zawsze w kierunku mozliwego ruchu ciała.

17.Podział ruchów punktu ze względu na przyspieszenie normalne i styczne.

Ze względu na przyspieszenie normalne wyróżniamy:

-ruch prostoliniowy an =0
-ruch krzywoliniowy an≠0

, a za względu na przyspieszenie styczne:

- jednostajny at=0

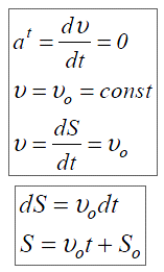
- jednostajnie zmienny

- niejednostajnie zmienny

18.Definicja ruchu kulistego bryły materialnej

Ruchem kulistym nazywamy, ruch ciała sztywnego, którego jeden punkt, zwany środkiem ruchu kulistego, jest unieruchomiony.

Ruchem kulistym nazywamy ruch, w czasie którego jeden z punktów bryły jest stale nieruchomy . Ruch kulisty jest obrotem dokoła chwilowej osi obrotu (oś ta zmienia swoje położenie w czasie)

19. Przyspieszenie Coriolisa - przypadki zerowania

Przyspieszenie Coriolisa określa wpływ ruchu względnego na ruch unoszenia i odwrotnie.

Przyspieszenie coriolisa jest równe 0 w następujących przypadkach:

- prędkość względna jest równa 0

- prędkość kątowa ruchu unoszenia jest równa 0 czyli ruch unoszenia jest ruchem postępowym

- wektor prędkości kątowej ruchu unoszenia jest || do wektora prędkości ruchu względnego

20.Ruch obrotowy bryły materialnej

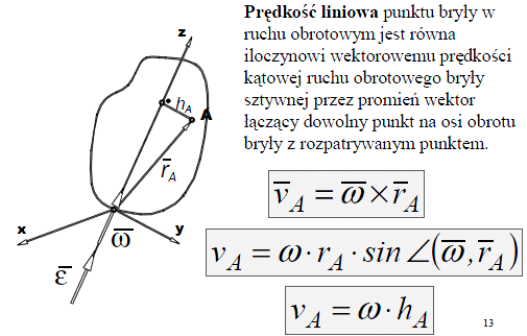
21.Zasada zachowania krętu.

Zasada zachowania krętu

kO(t)-kO(0)=0 czyli kO(t)=kO(0)=const lub jeżeli MO=0 to kO=const

Jeżeli moment główny sił zewnętrznych względem nieruchomego punktu redukcji O jest równy zeru, to kręt układu materialnego (bryły) względem tego punktu jest wielkością stałą.

22.Zasada D' Alemberta dla pkt materialnego

W ruchu punktu materialnego układ sił zewnętrznych równoważy się z siłą bezwładności.

W prostokątnym układzie współrzędnych mamy:

Powyzsze równania przedstawiają dynamiczne równania różniczkowe ruchu punktu materialnego w układzie współrzędnych prostokątnych.

Siła bezwładności jest równa iloczynowi masy punktu materialnego i przyspieszenia ruchu punktu. Jej kierunek jest taki sam jak kierunek wektora przyspieszenia, jej zwrot zaś jest przeciwny do zwrotu wektora przyspieszenia. B = -ma

Ruch takiego punktu możemy rozpatrywać jako ruch punktu swobodnego pod wpływem sił czynnych P i biernych R. Równanie wektorowe nieswobodnego punktu materialnego o stałej masie m ma postać:

23.Praca elementarna, moc i sprawność mechaniczna.

Pracą elementarną siły zmiennej F na przesunięciu elementarnym ds nazywamy iloczyn skalarny tej siły przez to przesunięcie elementarne.

ds = dx ×i + dy × j + dz × k

Pracę całkowitą od połoŜenia 1 do połoŜenia 2 siły zmiennej F otrzymamy całkując wyrażenie na pracę elementarną.

Moc

Mocą chwilową nazywamy stosunek pracy elementarnej do czasu dt, w którym została wykonana.

Moc jest skalarną wielkością fizyczną określającą pracę wykonaną w jednostce czasu przez układ fizyczny. Z definicji, moc określa wzór:

gdzie:

P - moc,

W - praca,

t - czas.

Sprawność - skalarna bezwymiarowa wielkość fizyczna określająca stosunek pracy lub (mocy) cej do pracy lub (mocy) włożonej.

Tak określoną sprawność można wyznaczyć następująco:

η =

Lo = Lu + Lt

gdzie:

η - sprawność,

Lo - praca włożona

Lu - praca użyteczna

Lt - praca tracona

24.Kryterium stateczności Mindinga - Dirichleta

W polu sil ciężkości równowaga punktu materialnego zachodzi w położeniu gdzie en pot osiąga ekstremum w szczególności równowaga stała zachodzi w położeniu gdzie en pot osiąga minimum.

25.Podaj przypadki redukcji dowolnego układu sił

Elementy redukcję dowolnego płaskiego układu sił:

- wektor główny Fg,

- moment główny Mg,

- parametr układu tzw. wyróżnik k

Wektor główny - równy jest sumie geometrycznej wszystkich sił układu traktowanych jako wektory swobodne. Wektor główny nie zależy od bieguna do którego redukujemy układ sił.

Moment główny (ogólny) - równy jest sumie momentów wszystkich sił względem bieguna redukcji O. Moment główny zależy od wyboru bieguna.

Parametr układu (wyróżnik) - to iloczyn skalarny wektora głównego i momentu ogólnego.

, czyli: k≤0

Przypadki redukcji dowolnego układu sił.

Wektor główny	Moment główny	Parametr układu k	Wynik redukcji
=0	=0	=0	Ukł. w równowadze
=0	≠0	=0	Para sił
≠0	=0	=0	Wypadkowa
≠0	≠0	≠0	Skrętnik, dwie siły skośne

Warunki równowagi dowolnego płaskiego układu sił

Dowolny płaski układ sił jest w równowadze jeśli algebraiczne sumy wszystkich rzutów sił na osie układu i suma momentów wszystkich sił względem dowolnie obranego bieguna na płaszczyźnie działania tych sił są równe zeru.

Warunki równowagi dowolnego przestrzennego układu sił

Przestrzenny dowolny układ sił znajduje się w równowadze jeżeli algebraiczne sumy rzutów wszystkich sił na trzy osie układu współrzędnych i algebraiczne sumy momentów wszystkich sił względem tych osi są równe 0.

26.Twierdzenie o trzech siłach

Tw o 3 siłach trzy nierównoległe siły na płaszczyźnie są w równowadze tylko wtedy, gdy tworzą wielobok zamknięty, a linie ich działania przecinają się w jednym punkcie.

27. Podaj równania równowagi dla przestrzennego, dowolnego układu sił.

Warunki równowagi dowolnego przestrzennego układu sił

Przestrzenny dowolny układ sił znajduje się w równowadze jeżeli algebraiczne sumy rzutów wszystkich sił na trzy osie układu współrzędnych i algebraiczne sumy momentów wszystkich sił względem tych osi są równe 0.

ΣFix=0 ΣMix=0

ΣFiy=0 ΣMiy=0

ΣFiz=0 ΣMiz=0

28.Jaki układ współrzędnych nazywamy naturalnym

Układ trzech osi: stycznej zwróconej w stroną ruchu, normalnej głównej zwróconej w stronę środka krzywizny toru i binormalnej zwróconej tak aby te osie w podanej kolejności tworzyły układ prawy nazywamy naturalnym układem współrzędnych

29.Prędkość i przyspieszenie punktu we współrzędnych kartezjańskich

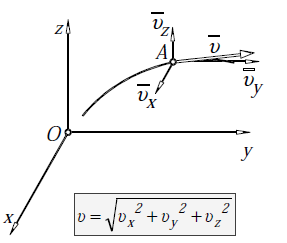
Prędkość

Składowe przyspieszenia są równe drugim pochodnym względem czasu odpowiednich współrzędnych poruszającego się punktu

a = axi + ay j + azk

31. Prędkość i przyspieszenie punktu bryły w ruchu płaskim.

32.Pęd i kręt punktu materialnego

Pęd punktu materialnego jest to wektor o module m razy większym od modułu wektora prędkości, mający kierunek i zwrot wektora prędkości.

Krętem punktu materialnego względem dowolnego bieguna O nazywamy wektor równy iloczynowi wektorowemu promienia wektora i wektora pędu poruszającego się punktu.

Kręt to moment pędu.

33.Energia mechaniczna i zasada jej zachowania.

W polu potencjalnym suma energii kinetycznej i potencjalnej jest niezależna od położenia punktu materialnego w tym polu i ma wartość stałą.

Ek + Ep = const

Sumę energii kinetycznej i potencjalnej nazywamy energią mechaniczną.

Ek + Ep = Em

W dowolnym ruchu przebiegającym bez tarcia (i innych strat energii) energia mechaniczna układu izolowanego jest stała.

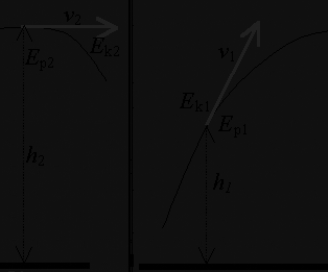
W sytuacji na rysunku: Ek1 + Ep1 = Ek2 + Ep2

34.Energia kinetyczna bryły w ruchu postępowym, obrotowym i płaskim.

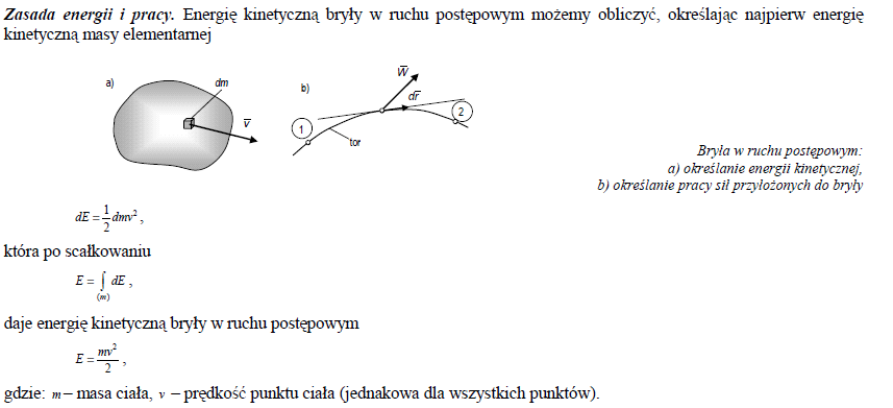
Energia kinetyczna bryły w ruchu:

Postępowym

Ek =

Obrotowym

Ek =

Płaskim

Ek =

35.Praca stałej siły na prostoliniowym przesunięciu.

Jeżeli ruch ciała jest prostoliniowy a wektor siły jest stały, pracę tej siły określa wzór

L = F x s => L = |F|*|s| * cos(F,s)

W ogólnym przypadku, gdy wektor siły nie jest stały lub przemieszczenie nie jest prostoliniowe, praca jest sumą prac wykonanych na niewielkich odcinkach, na tyle małych, że spełnione są powyższe warunki. Wyraża ją wówczas wzór całkowy

gdzie:

W - praca,

L - całkowita droga, jaką pokonuje ciało,

- siła,

- wektor przesunięcia,

α - kąt między wektorem siły i przesunięcia.

Jednostką miary pracy w układzie jednostek miar SI jest dżul (J) określany jako niuton metr:

19

---